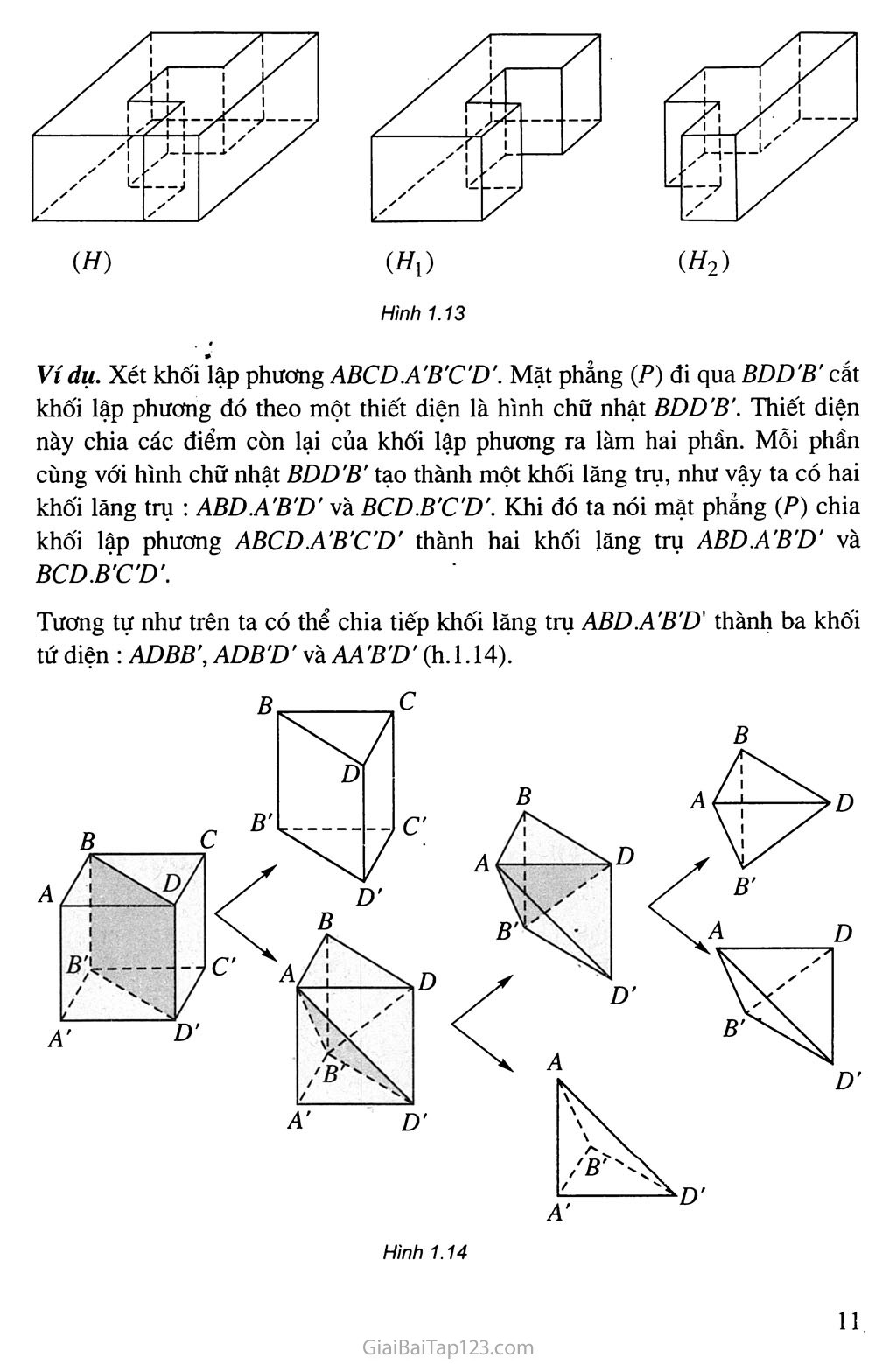
SGK Hình Học 12 - Bài 1. Khái niệm về khối đa diện

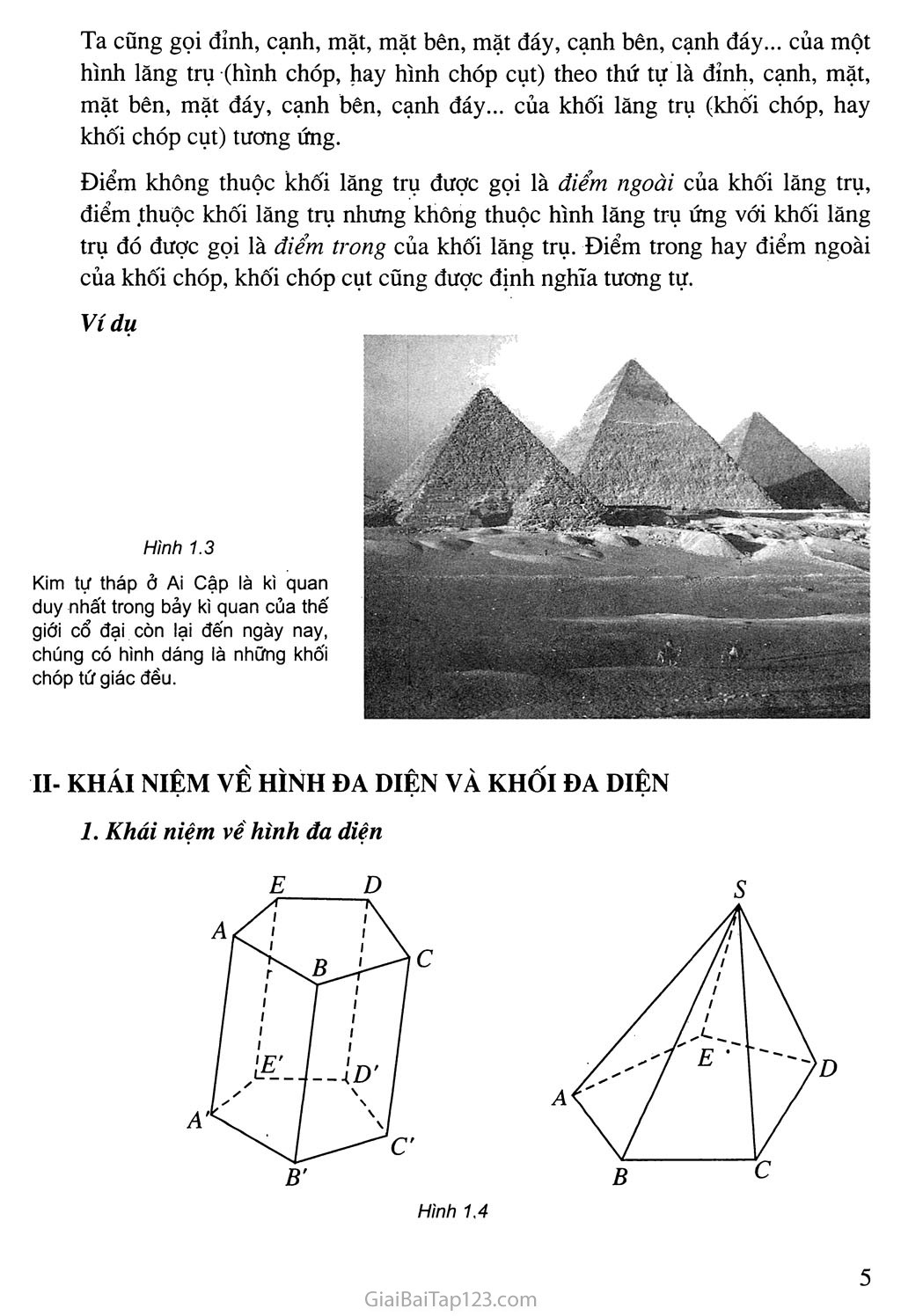
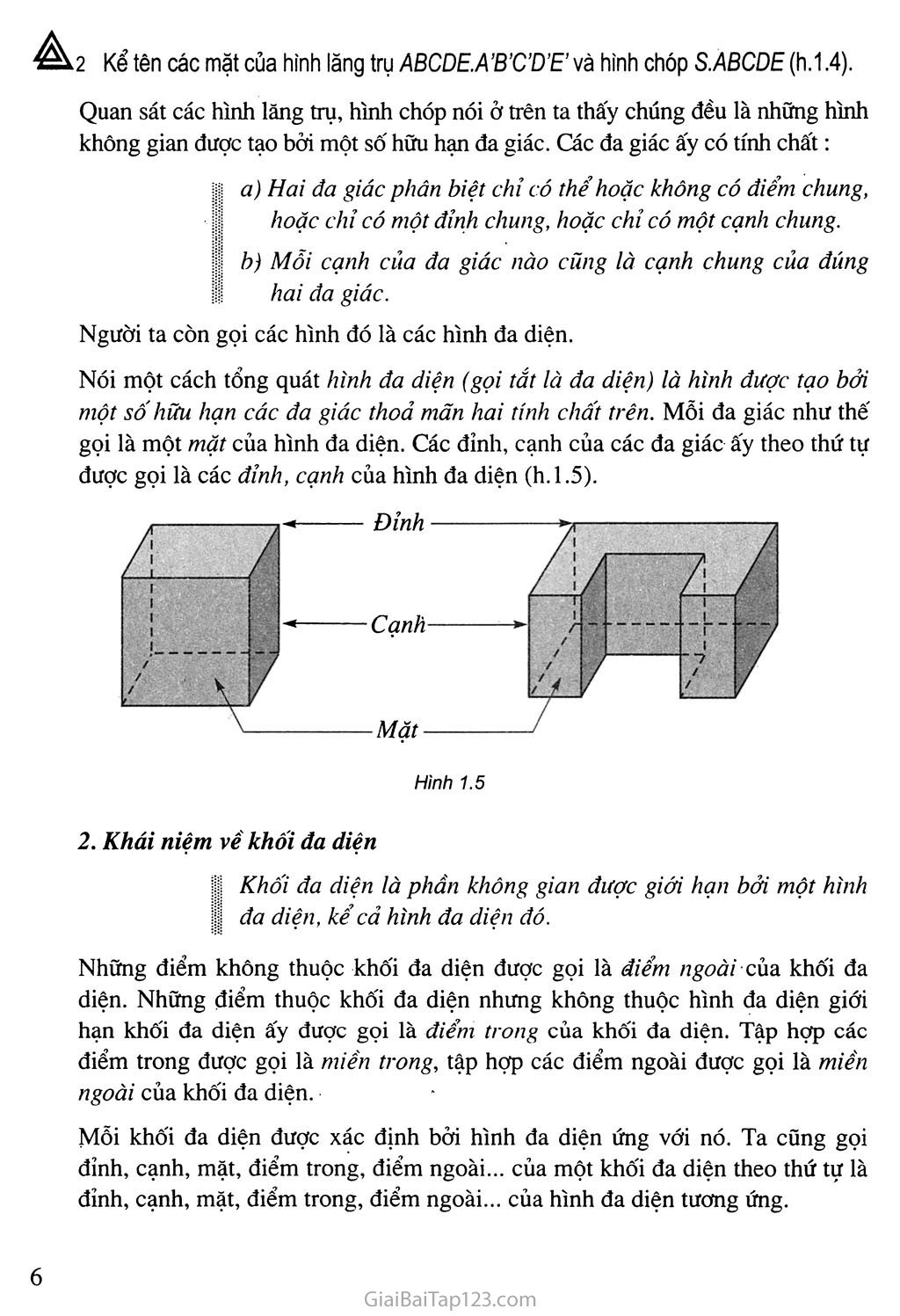
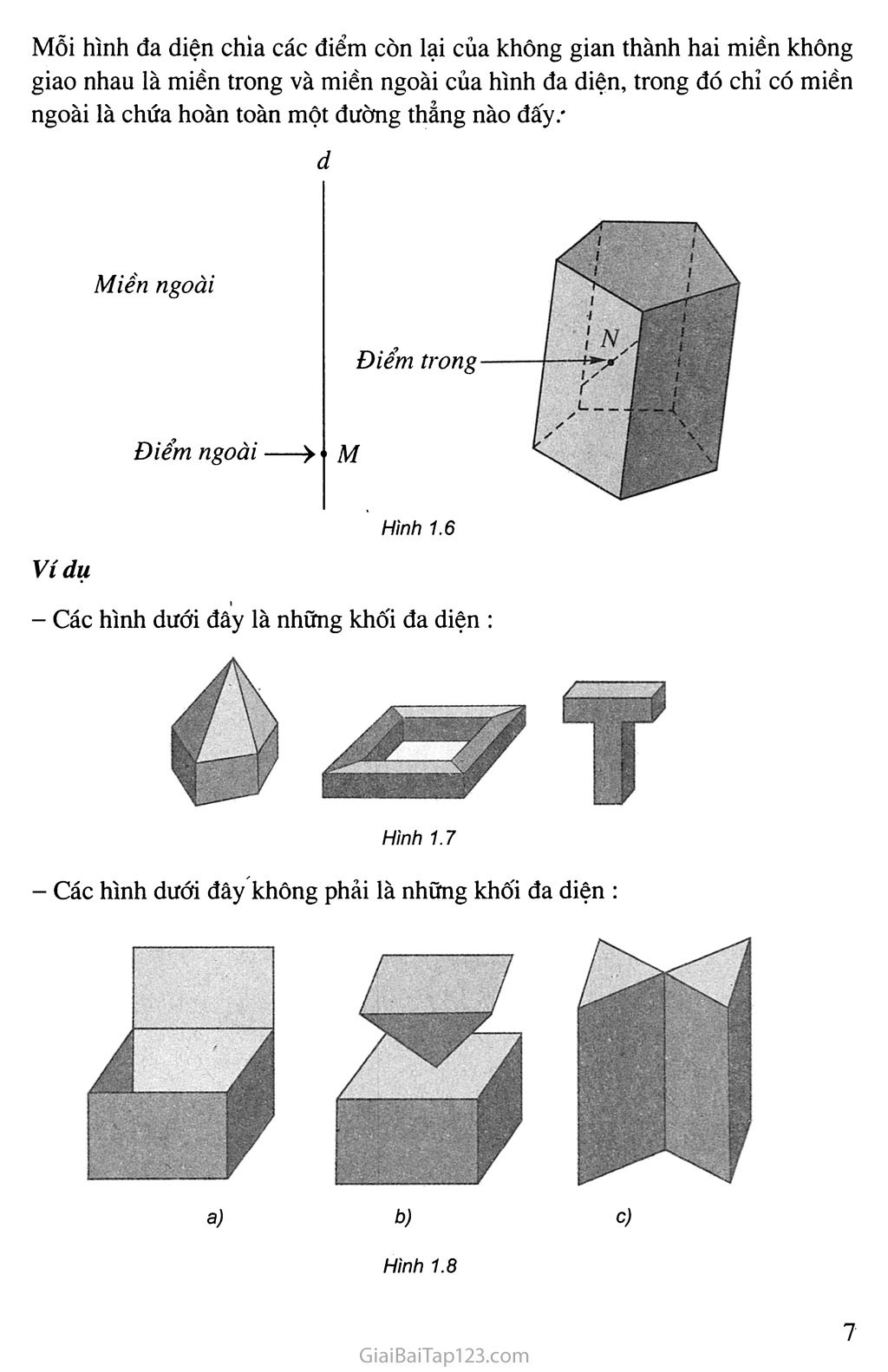
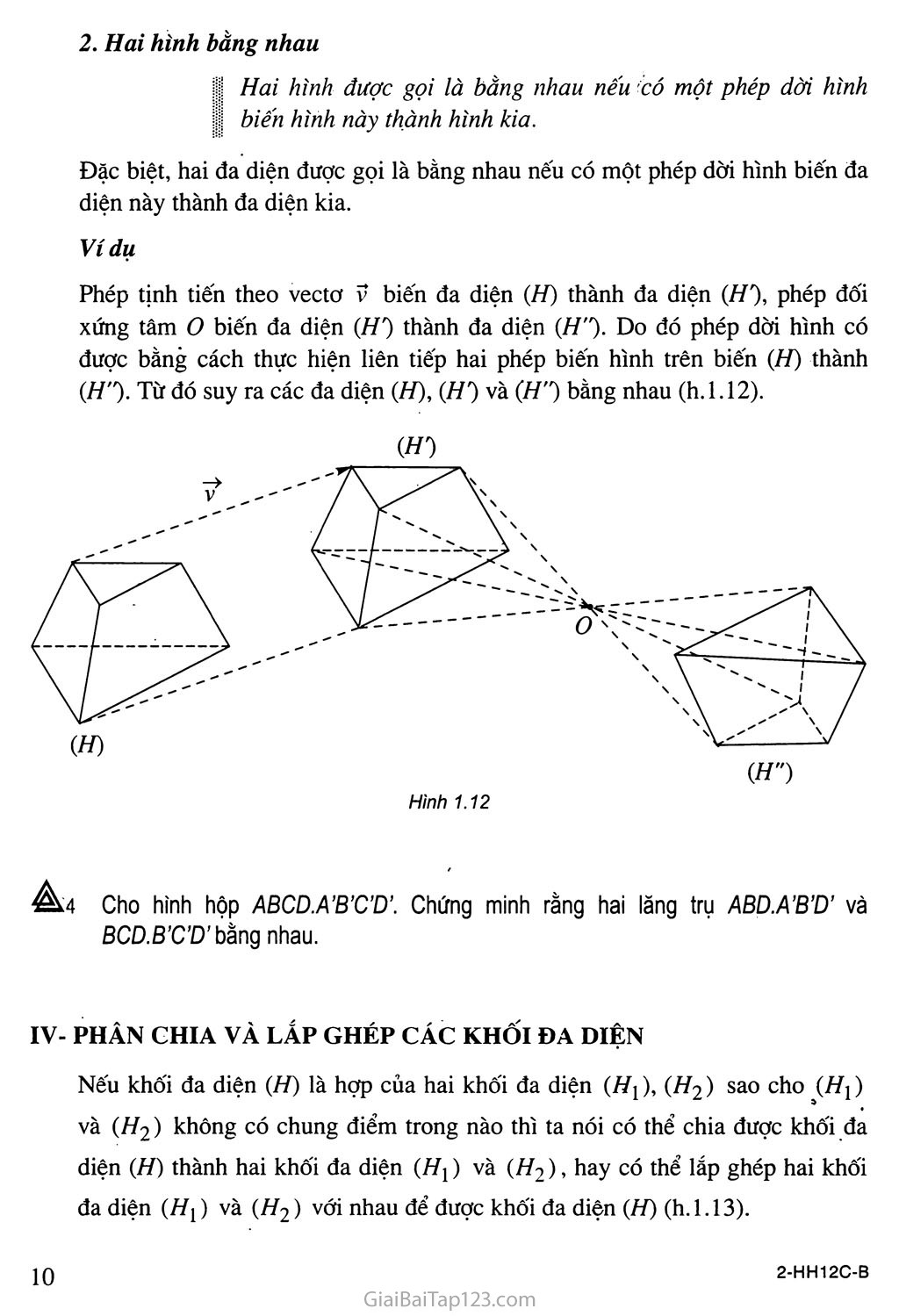
KHỐI ĐA DIỆN
Khái niệm về khôi đa diện ♦♦♦ Khối đa diện đều ♦í’ Thể tích khối đa diện
Một khối muối ăn
Trong thực tế chúng ta thường gặp những vật thể không gian được giới hạn bởi các đa giác như viên gạch, khối lập phương, kim tự tháp Ai Cập, tinh thể của một số hợp chất hoá học như muối ăn, phèn chua .... Những vật thể đó được gọi là những khối đa diện, về mặt toán học, việc định nghĩa chính xác khối đa diện không đơn giản. Trong chương này ta chỉ giới thiệu khái niệm về khối đa diện, khối đa diện đều và đưa ra công thức tính thể tích của một số khối đa diện quen thuộc.
Hình 1.1
§ĩ. KHÁI NIỆM VÊ KHÔI ĐA DIỆN
Áki Nhắc lại định nghĩa hình lăng trụ và hình chóp.
KHỐI LẢNG TRỤ VÀ KHỐI CHÓP
Quan sát khối rubic trong hình 1.1, ta thấy các mặt ngoài của nó tạo thành một hình lập phương. Khi đó ta nói khối rubic có hình dáng là một khối lập phương. Như vậy có thể xem khối lập phương là phần không gian được giới hạn bởi một hình lập phương, kể cả hình lập phương ấy.
Tương tự, khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy, khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy, khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.
Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó. Chẳng hạn ứng với hình lăng trụ lục giác ABCDEF.A'B'C'D'E'F' ta có khối lăng trụ lục giác ABCDEF .AB'C'DE'F', ứng với hình chóp tứ giác đều S.ABCD ta có khối chóp tứ giác đều S.ABCD (h.1.2)...
Ta cũng gọi đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh bên, cạnh đáy... của một hình lăng trụ (hình chóp, hay hình chóp cụt) theo thứ tự là đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh bên, cạnh đáy... của khối lăng trụ (khối chóp, hay khối chóp cụt) tương ứng.
Điểm không thuộc khối lăng tru được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ ứng với khối lãng trụ đó được gọi là điểm trong của khối lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương tự.
Ví du
Hình 1.3
Kim tự tháp ở Ai Cập là kì quan duy nhất trong bảy kì quan của thế giới cổ đại còn lại đến ngày nay, chúng có hình dáng là những khối chóp tứ giác đều.
KHÁI NIỆM VỂ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
Khái niệm về hình đa diện
Kể tên các mặt của hình lăng trụ ABCDE.A’B'C’D’E’ và hình chóp S.ABCDE (h.1.4).
Quan sát các hình lăng trụ, hình chóp nói ở trên ta thấy chúng đều là những hình không gian được tạo bởi một số hữu hạn đa giác. Các đa giác ấy có tính chất:
ịiịỊ a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
I b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 1 hai đa giác.
Người ta còn gọi các hình đó là các hình đa diện.
Nói một cách tổng quát hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thoả mãn hai tính chất trên. Mỗi đa giác như thế gọi là một mặt của hình đa diện. Các đỉnh, cạnh của các đa giác ấy theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện (h. 1.5).
Khái niệm về khối đa diện
I Khối đa diện là phần không gian được giới hạn bởi một hình I đa diện, kể cả hình đa diện đó.
Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Nhũng điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện. Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
Mỗi khối đa diện được xác định bởi hình đa diện ứng với nó. Ta cũng gọi đỉnh, cạnh, mặt, điểm trong, điểm ngoài... của một khối đa diện theo thứ tự là đỉnh, cạnh, mặt, điểm trong, điểm ngoài... của hình đa diện tương ứng.
Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy/
d
- Các hình dưới đây là những khối đa diện :
Hình 1.7
- Các hình dưới đây không phải là những khối đa diện :
- Những viên, kim cương có hình dạng là những khối đa diện :
Hình 1.9
4=^3 Giải thích tại saơ hình 1,8c không phải là một khối đa diện ?
HAI ĐA DIỆN BẰNG NHAU
Phép dời hình trong không gian
Phép biến hình và phép dời hình trong không gian được định nghĩa tương tự như trong mặt phẳng.
Trong không gian, quy tắc đặt tương ứng mỗi điểm M với I điểm M' xác định duy nhất được gọi là một phép biến hình
trong không gian.
I Phép biêh hình trong không gian được gọi là phép dời hình 1 nếu nó bảo toàn khoảng cách giữa hai điểm tuỹ ý.
Ví dụ
Trong không gian, các phép biến hình sau đây là những phép dời hình :
a) Phép tịnh tiên theo vectơ V, là phép biến hình biến mỗi điểm M thành điểm M' sao cho MM' = V (h.l.lOa).
M
M'
Hình 1.10b)
Phép đối xứng qua mặt phẳng (P), là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M' sao cho (P) là mặt phẳng trung trực của MM' (h.l.lOb).
Nếu phép đối xứng qua mặt phẳng (F) biến 'hình (//) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).
Phép đối xứng tâm o, là phép biến hình biến điểm o thành chính nó, biến mỗi điểm M khác o thành điểm M' sao cho 0 là trung điểm của MM' (h. 1.1 la).
Nếu phép đối xứng tâm o biến hình (77) thành chính nó thì 0 được gọi là tâm đối xứng của (77).
d) Phép đối xứng qua đường thẳng A (hay phép đối xứng qua trục À), là phép biến hình biến mọi điểm thuộc đường thẳng A thành chính nó, biến mỗi điểm M không thuộc A thành điểm M' sao cho A là đường trung trực của MM' (h.l.llb).
Nếu phép đối xúng qua đường thẳng A biến hình (77) thành chính nó thì A gọi là trục đối xứng của (77).
Nhận xét
Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
Phcp dời hình bicn da diện (11) thành da diẹn Ự7 j, biên dinh, cạnh, mặt của (77) thành đỉnh, cạnh, mật tương ứng cua (H').
Hai hình bằng nhau
I Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Đặc biệt, hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
Ví dụ
Phép tịnh tiến theo vectơ V biến đa diện (H) thành đa diện (//'), phép đối xứng tâm o biến đa diện (//') thành đa diện (//"). Do đó phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình trên biến (//) thành (//"). Từ đó suy ra các đa diện (/7), (//') và (//") bằng nhau (h. 1.12).
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.
IV- PHÂN CHIA VÀ LẮP GHÉP CÁC KHỐI ĐA DIỆN
Nếu khối đa diện (H) là hợp của hai khối đa diện (//ị ), (//2) sao cho (//ị ) và (//2) không có chung điểm trong nào thì ta nói có thể chia được khối đa diện (//) thành hai khối đa diện (Hỵ) và (//2), hay có thể lắp ghép hai khối đa diện (//)) và (//2) với nhau để được khối đa diện (//) (h.1.13).
Hình 1.13
(H)	(Hj)	(tf2)
Ví dụ. Xét khối lập phương ABCDA'B'C'D'. Mặt phẳng (/’) đi qua BDD'B' cắt khối lập phương đó theo một thiết diện là hình chữ nhật BDDB'. Thiết diện này chia các điểm còn lại của khối lập phương ra làm hai phần. Mỗi phần cùng với hình chữ nhật BDD'B' tạo thành một khối lăng trụ, như vậy ta có hai khối lăng trụ : ABD.AB'D' và BCD.B'C'D'. Khi đó ta nói mặt phẳng (P) chia khối lập phương ABCD.A'B'C'D' thành hai khối lãng trụ ABD.AB'D' và BCD.B'C'D’.
Tương tự như trên ta có thể chia tiếp khối lăng trụ ABD.A'B'D' thành ba khối tứ diện : ADBB', ADB'D' vaAA'B’D' (h.l.14).
Hình 1.14
Làm theo quá trình ngược lại ta có thể ghép khối lăng trụ BCD.B'C'D' và các khối tứ diện ADBB', ADB'D', AA'B'D' với nhau để được khối lập phương ABCD.A’B'C'D'.
Nhận xét
Một khối đa diện bất kì luồn có thể phân chia được thành những khối tứ diện.
BÀI TẬP
Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn. Cho ví dụ.
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của một số lẻ mặt thì tổng số các đỉnh của nó phải là một sô' chẵn. Cho ví dụ.
Chia một khối lập phương thành năm khối tứ diện.
Chia một khối lập phương thành sáu khối tứ diện bằng nhau.
Định nghĩa đa diện và hhối đa diện
ơ đầu chương, chúng ta mới chỉ trình bày sơ lược về các khái niệm đa diện và khối đa diện. Bây giờ ta sẽ trình bày một cách chính xác hơn những khái niệm đó.
Khái niệm đa diện và khối đa diện có thê’ được hiểu theo nhiều cách khác nhau. Đa diện và khối đa diện vừa dược trình bày trong chưong I dưa vào đinh nghĩa sau đây.
Định nghĩa
Hình da diện (gọi lãi la da dan) là hìnli dưực tạo bưi mọt so hữu hạn cúc da giác, gọi là các mật cùa hình da diện, thoá mãn các tính chất sau :
Hai mặt phẩn biệt chỉ có thể hoặc không giao nhau hoặc có một đinh chung, hoặc có một cạnh chung.
Mỗi cạnh thuộc một mặt là cạnh chung của đúng hai mặt.
Cho hai mặt s và S', luôn tồn tại một dãy các mặt so, Sị, ..., s„ sao cho so trùng với s, S,J trùng với S' và bất kì hai mặt Sị, Sị+ỵ nào (0 < i < n -1) cũng đều có một cạnh chung.
Các đình, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.
Ví dụ
Hình (//) trong hình 1.15 là hình tạo bởi hai hình lập phương chỉ chung nhau một đỉnh. Khi đó (//) không thoả mãn tính chất c) nên nó không phải là một hình đa diện.
Từ định nghĩa trên, người ta chứng minh được định lí sau gọi là định lí Gioóc-đan (Jordan) trong không gian.
Định lí
Môi đa diện chia các điếm còn lại của không gian thành hai miên sao cho :
Hai điểm thuộc cùng một miền luôn có thể nối với nhau bằng mọt đường gấp khúc nằm hoàn toàn trong miền đó.
Mọi đường gấp khúc nối hai điểm thuộc hai miền khác nhau đều có điểm chung với đa diện.
(H)
Hình 1.16
Có một và chỉ một miền chứa hoàn toàn một đường thẳng nào đấy.
Miền chứa hoàn toàn một đường thẳng nào đấy được gọi là »ỉz'é>7 ngoài của đa diện, miền còn lại được gọi là miền trong của đa diện. Điểm thuộc'miền ngoài gọi là điểm ngoài, điểm thuộc miền trong gọi là điểm trong của đa diện.
Trong hình 1.16, A là điểm trong, B, c, D là điểm ngoài của hình đa diện (//). Miền ngoài của (//) chứa đường thẳng d.
Định nghĩa
Đa cliện cùng với miền trong của nó được gọi là một khối đa diện.
Trong thực tế, chúng ta thường gặp những vật thể có hình dáng là những khối đa diện. Từ những công trình vĩ đại như kim tự tháp Ai Cập, những toà nhà cao tầng hiện đại đến những vật thể nhỏ như tinh thể của các hợp chất : đường, muối, thạch anh... đều là những khối đa diện. Do đó, việc nghiên cứu các khối đa diện không những làm phong phú thêm các kiến thức về hình học mà còn góp phần giải quyết nhiều bài toán thực tiễn, phục vụ cuộc sống con người.