SGK Hình Học 12 - Bài 2. Phương trình mặt phẳng

§2. PHƯƠNG TRÌNH MẶT PHANG
Trong hình học không gian ở lớp 11 ta đã biết một số cách xác định mặt phẳng, chẳng hạn như xác định mặt phẳng bằng ba điểm không thẳng hàng, bằng hai đường thẳng cắt nhau, ... . Bây giờ ta sẽ xác định mặt phẳng bằng phương pháp toạ độ.
Các bức tường của toà nhà cao tầng hiện đại cho ta hinh'anh của mặt phẳng trong không gian
I- VECTƠ PHÁP TUYẾN CƯA MẶT PHANG
Định nghĩa
Cho mặt phalli’ (a). Nếu vectơ ri khác 0 và có giá vuông góc VƠI mật pliấng.((X) thi ri dược gọt la vectơ pháp tuyến cùa (a).
E§= Chú ý. Nếu « là vectơ pháp tuyến của một mặt phẳng thì kh với k0, cũng là vectơ pháp tuyến của mặt phẳng đó.
(Bài toán
Trong không gian Oxyz cho mặt phẳng (cộ và hai vectơ không cùng phương à = (ữỊ; ữ2; ỡ3), b = (bỵ; /?2 ; ^3) c° giá song song hoặc nằm trong mặt phẳng (cộ. Chứng minh rằng mặt phảng (cr) nhận vectơ
n - («2^3 -ơ3^2 ’ ứ3^1 - ứ1^3 ’ a\^1 - a2^\) làm vectơ pháp tuyến.
Tacó: a.n - c/ị (c/2^53-d3Z?2) + #2(^1 - Ơ1^3) +
= (aỵa^by -a^aỵbý) + (a^aỵb^ -ữ|ữ3/?2) + (a^aybỵ -ữ3ữ2Z?i)
= 0.
Tương tự b.n - 0.
Vậy vectơ n vuông góc với cả hai vectơ ã và b, có nghĩa là giá của nó vuông góc với hai đường thẳng cắt nhau của mặt phảng (cộ (h.3.4). Suy ra giá của n vuông góc với mặt phẳng (cc). Vì a, b không cùng phương nên các toạ độ của ĩĩ không đồng thời bằng 0,
suy ra «	0. Do đó vectơ n là
một vectơ pháp tuyến của mặt phẳng (à).
Vectơ h xác định như trên được gọi là tích có hướng (hay tích vectơ) của hai vectơ ã và b, kí hiệu là n = ả /\b hoặc n - [ứ, b].
Trong không gian Oxyz cho ba điểm 4(2 ; -ì ; 3), 6(4 ; 0 ; 1), C(—10 ; 5 ; 3). Hãy tìm toạ độ một vectơ pháp tuyến của mặt phẳng [ABC).
II- PHƯƠNG TRÌNH TổNG QUÁT CỦA MẶT PHANG
(Bải toán ỉ
Trong không gian Oxyz cho mặt phẳng (cộ đi qua điểm Mồ (.v0 ; y0 ; z0) và nhận n (Ẩ ; B ; C) làm vectơ pháp tuyến. Chứng minh rằng điều kiện cần và đủ để điểm M(x thuộc mặt phẳng (cộ.là :
Â(x - x0) + B(y - y0) + C(z - z0) = 0.
ỹiải
Ta có MqM = (x - Xq y - yG ■, z - z0) (h.3.5)
M e (cc) MqM c (a) ĩĩ 1 MqM
 Ĩi.MqM - 0
 A(x - x0) + B(y- y0) + C(z - z0) = 0.
(Bài toán 2
Trong không gian Oxyz, chứng minh rằng tập hợp các điểm M(x ; y ; z) thoả mãn phương trình Ax + By + Cz + D = 0 (trong đó các hệ số A, B, c không đồng thời bằng 0) là một mặt phẳng nhận vectơ ĩĩ = (A ; B ; C) làm vectơ pháp tuyến.
Ta lấy điểm Mq(xq ; y0 ; Zo) sao cho A,v0 + By$ + Cz0 + D = 0 (chẳng hạn nếu A * 0 thì ta lấy A'o = —; y0 = z0 = 0).
Gọi (a) là mặt phẳng đi qua điểm Mữ và nhận « = (Â ; B ; C) làm vectơ pháp tuyến. Ta có :
Me(a) a A(x - x0) + B(y- y0) + C(z - z0) = 0 Ax + By + Cz — (Ar0 + Byữ + Cz0) = 0 Ax + By + Cz + D = 0 vì D - - (Ax0 + By0 + Cz0).
Từ hai bài toán trên ta có định nghĩa sau.
Định nghĩa
I Phương trình có dạng Ax + By + Cz + D = 0, trong đó A, B, c I không đồng thời bằng 0, được gọi là phương trình tổng quát I của mặt phẳng.
Nhận xét
Nếu mặt phẳng (a) có phương trình tổng quát là Ax + By + Cz + D = 0 thì nó có một vectơ pháp tuyến là h (A ; B ; C).
Phương trình mặt phẳng đi qua điểm M0(x0 ; y0 ; z0) nhận vectơ h (A ; B ; C) • khác 0 làm vectơ pháp tuyến là A(x - Xq) + B(y — y0) + C(z - z0) = 0.
Hãy tìm một vectơ pháp tuyến của mặt phẳng (ữ): 4x- 2y- 6z + 7 = 0.
Lập phương trình tổng quát của mặt phẳng (MNP) với A4(1 ; 1 ; 1), /V(4 ; 3 ; 2),
P(5;2;1).
Hình 3.6
Các trường hợp riêng
Trong không gian Oxy: cho mặt phẳng (ạ):
/t.v + By + Cz + D — 0.	(1)
a) Nêu /9 = 0 thì gốc toạ độ o có loạ độ thoá mãn phương trình của mặt phang (Ýr). Vây (à) đi qua gốc toạ đọ o (h.3.6).
b) Nếu một trong ba hệ số A, B. c bằng 0, chẳng hạn A -0 thì mặt phẳng (cr)
có vectơ pháp tuyến là n = (0 ; B ; C). Ta có n.i = 0. Do i ià vectơ chỉ phương của Ox nên ta suy ra (cr) song song hoặc chứa trục Ox (h.3.7a).
Hình 3.7
Nếu 8 = 0 hoặc c = 0 thì mặt phẳng (ữ) có đặc điểm gì ?
Nếu hai trong ba hệ số A, B, c bằng 0, ví dụ A = B = 0 và c 0 thì từ trường hợp b) ta suy ra mặt phẳng (cộ song song với Ox và Oy hoặc (cộ chứa Ox và Oy. Vậy (cộ song song hoặc trùng với mặt phẳng (ơxy) (h.3.8a).
Cz + D = 0 a)
b)
Hình 3.8
c)
Nếu A = c - 0 và B * 0 hoặc nếu B = c = 0 và >4 * 0 thì mặt phẳng (à) có đặc điểm gì ?
Nhận xét
Nếu cả bốn hệ sô A, B, c, D đêu
khác 0 thì bằng cách đặt a - -—■>
A
b = ——’ c = —ta có thế đưa
B c
phương trình (1) về dạng sau đây :
(2)
X' y Z , - + 2- + -=l . a b c
Khi đó mặt phẳng {à) cắt các trục Ox, Oy, Oz lần lượt tại các điểm có toạ độ là {a ; 0 ; 0), (0 ; ồ ; 0), (0 ; 0 ; c). Người ta còn gọi phương trình (2) là phương trình của mặt phẳng theo đoạn chắn (h.3.9).
Hình 3.9
Ví dụ. Trong không gian Oxyz cho ba điểm M( 1 ; 0 ; 0), N(0 ; 2 ; 0), P{0 ; 0 ; 3). Hãy viết phương trình mặt phảng {MNP).
giải
Áp dụng phương trình của mặt phẳng theo đoạn chắn, ta có phương trình của mặt phẳng {MNP) là :
— + 37 + -7 = 1 hay 6x + 3y + 2z -6 = 0.
12 3
III- ĐIỂU KIỆN ĐỂ HAI MẶT PHANG song song, vuông góc
6 Cho hai mặt phẳng (ỡ) và (/3) có phương trình (ỡộ :x-2y + 3z + 1 =0,
{/3): 2x - 4y + 62 + 1 =0.
Có nhận xét gì về vectơ pháp tuyến của chúng ?
Trong không gian Oxyz cho hai mặt phẳng (ƠỊ) và («2) có phương trình : A Ị.X' + BịV + cJZ + Dị — 0,
(<9^2) : A2X + B-)Ỵ + C2Z + z?2 =
Khi đó («|) và (a2) có hai vectơ pháp tuyến lần lượt là
= 0^1 ỉ Bị; Cj),
«2 = (A2 ỉ ^21 ^2)-
Ta xét điều kiện để hai mặt phẳng (ttj) và (cr2) song song hoặc vuông góc với nhau.
Điều kiện để hai mặt phẳng song song
Ta nhận thấy haì mặt phẳng (ớq) và (ư2) song song hoặc trùng nhau khi và chỉ khi chúng cùng vuông góc với một đường thẳng, nghĩa là khi và chỉ khi hai vectơ pháp tuyến «1 và «2 của chúng cùng phương (h.3.10).
Khi đó ta có :	= £«2 •
Nếu Dỵ = kD2 thì ta có (ữj) trùng với (ơ2).
Nếu Dị *kũ2 thì («1) song song với (a2).
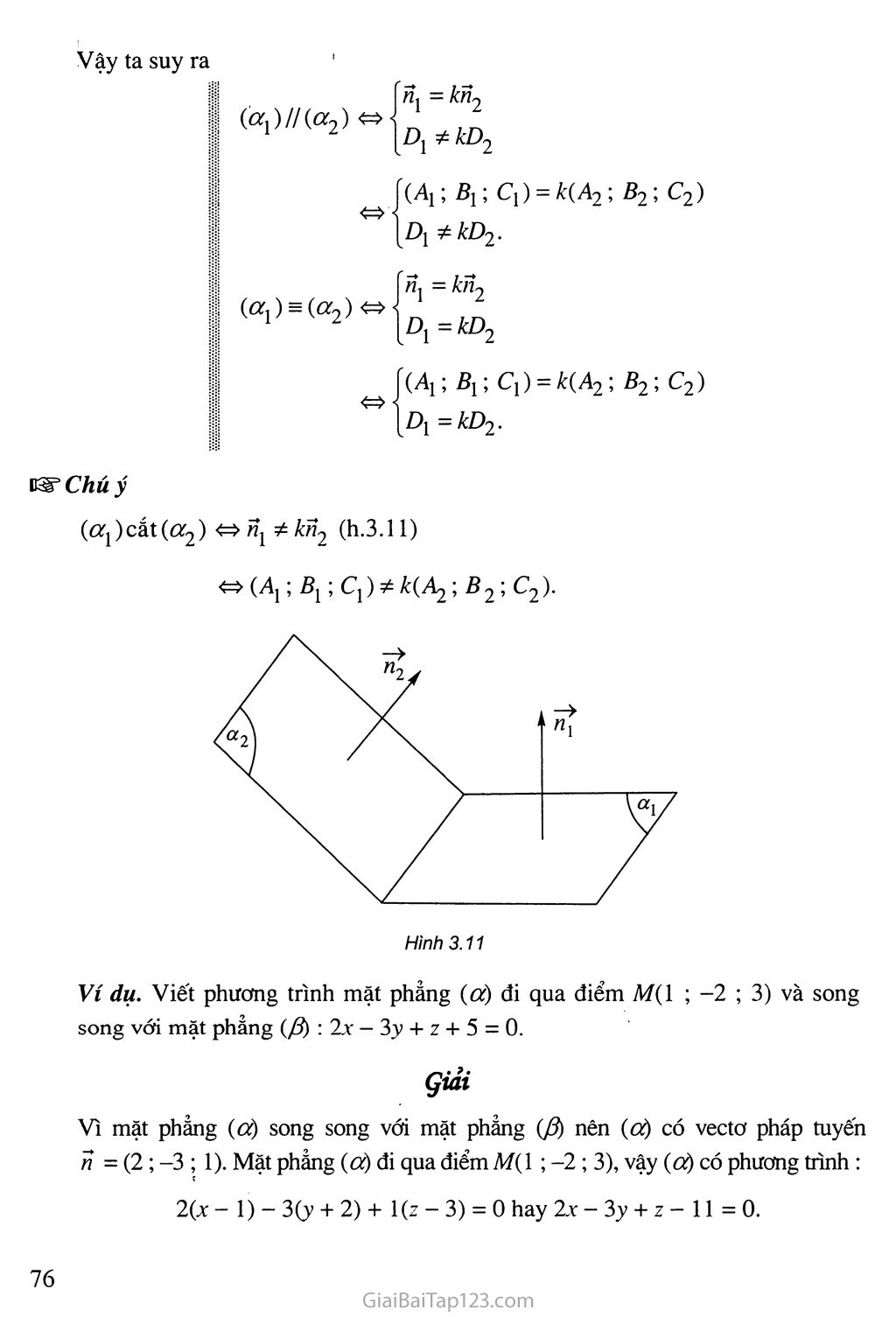
Vậy ta suy ra
Ã?1 - kĩĩ-1 Dị kD~>
(Aị ; Bị ; Cị) - Ẩ.'(Â2; Bọ ’ ^2) Dị kD% ■
(ữỌ^Cớ^)
«1 = *«2 Dỵ = kD^
(Âị ; Bị ; C|) - £(^2; ^2’ O’)
Dỵ - kŨ2 ■
vSsChúý
(ơj) cắt («2) /7j	£«2 (h.3.11)
(Âj; Bỵ;	B2; C2).
Hình 3.11
Ví dụ. Viết phương trình mặt phẳng (ộ) đi qua điểm A7(l ; -2 ; 3) và song song với mặt phẳng (/J) :2x — 3y + z + 5 = 0.
Vì mặt phẳng (6Ộ song song với mặt phảng (J3) nên (6Ộ có vectơ pháp tuyến
ĩì = (2 ; -3 ; 1). Mặt phẳng (ữ) đi qua điểm 37(1 ; -2 ; 3), vậy (ữộ có phương trình :
2(x - 1) - 3(y + 2) + 1 (z - 3) = 0 hay 2x - 3y + z - 11 =0.
Điều kiện để hai mặt phẳng vuông góc
Hình 3.12
Ta nhận thấy hai mặt phẳng (ƠỊ) và (cz2) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến /ì] và «2 tương ứng của chúng vuồng góc với nhau (h.3.12). Vậy ta có điều kiện :
I (cq)±(a2) n\.n-> =0
4jÂ2 + B \B~) + c ỊỨO = 0.
Ví dụ. Viết phương tình mặt phẳng (cộ đi qua hai điểm A(3 ; 1 ; -1), 5(2 ; -1; 4) và vuông góc với mặt phẳng (j3) có phương trình :
2x - y + 3z - 1 = 0.
ỹiđí
Gọi rip là vectơ pháp tuyến của mặt phẳng (J3). Hai vectơ không cùng phương có giá song song hoặc nằm trên (a) là :
Ã5 = <-l;-2;5)và^=(2;-l;3).
Do đó mặt phẳng (cộ có vectơ pháp tuyến :
na = AB /\hp - (-1 ; 13 ; 5).
Vậy phương trình của (cr) là :
-l(.v-3)+ 13(y- l) + 5(z + l) = 0 X- 13y-5z + 5 = 0.
IV- KHOẢNG CÁCH TỪ MỘT ĐlỂM đến một mặt phang
Định lí
Trong không gian Oxyz, cho mặt phẳng (a) có phương trình Ax + By + Cz + D = 0 và điểm M0(x0;y0; z0). Khoảng cách từ điểm Mq đến mặt phẳng (a), kí hiệu là d( Mq, (a)), được tính theo công thức :
d(M0, (a)) =
ÂA'o + ỔVq + Cz0 + D
+ B-+C-
chứng minh
Gọi Mị(Xị ; Vj ; Zị) là hình chiếu vuông góc của A/q trên (ạ) (h.3.13). Xét hai vectơ
= (x0 -	; y0 - }’i ; z0 - Zi)
và h = (Â ; B ; C), ta thấy Mị Mq và h cùng phương vì giá của chúng cùng vuông góc với (ỡộ. Suy ra :
|Mị Mq I .1/71 = |a/ị M0./ĩ|
Hình 3.13
= |A(x0 -*1) + B&o - ) + c(z0 - )|
- |Av0 + 5v0 +Czq + (-Aa'i - ỔVị -Czị)| .	(1)
Mặt khác vì Mị thuộc (ợ) nên ta có :
Avị + By ỵ + Czị + D — 0
hay D = -Ayị - By\ -Czỵ.	(2)
Thay (2) vào (1) ta được	= |Av0 + Byữ + Czq + D\.
Gọi khoảng cách từ điểm Mq đến mặt phẳng (ạ) là <7( Mq , (à)).
Vậy<7(M0, (ộ)) - IMịMqI
I Axq + ByQ + Cz0 + dị
l«l
I Axq + ByQ + Czq + D|
Vâ2+B2+C2
Ví dụ 1. Tính khoảng cách từ gốc toạ độ và từ điểm M(1 ; -2 ; 13) đến mặt phẳng (a): 2x - 2y - z + 3 = 0.
Áp dụng công thức tính khoảng cách ở trên ta có :
d(M, (cộ) = 1 ,	;	; = Ị.
V22 +(-2)2 +(-l)2 3
Ví dụ 2. Tính khoảng cách giữa hai mặt phẳng song song (à) và (/?) cho bởi các phương trình sau đây :
(a): X + 2y + 2z + 11 =0,
(yổ) : X + 2y + 2z + 2 = 0.
Ta biết khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì của mặt phẳng này tới mặt phẳng kia.
Ta lấy điểm M(0 ; 0 ; -1) thuộc (/?), kí hiệu ú?((cc), (/?)) là khoảng cách giữa hai mặt phảng (ậ) và (J3), ta có :
</((«), Cổ)) = rf(M, (o» =1	=—I = 4 = 3.
.;2	3
Tính khoảng cách giữa hai mặt phẳng (ữ) và ($ cho bởi các.phương trình sau đây: (ữ): X- 2 = 0,
CỔ):x-8 = 0.
BÀI TẬP
Các bài tập sau đây đều xét trong không gian Oxyz.
Viết phương trình của mặt phẳng :
Đi qua điểm A7(l ; -2 ; 4) và nhận « - (2 ; 3 ; 5) làm vectơ pháp tuyến ;
Đi qua điểm /4(0 ; -1 ; 2) và song song với giá của mỗi vectơ ỉ7 = (3 ; 2 ; 1) và v-(-3;0;l);
Đi qua ba điểm Â(-3 ; 0 ; 0), 5(0 ; -2 ; 0) và C(0 ; 0 ; -1).
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2 ; 3 ; 7), 5(4; 1-3).
a) Lập phương trình của các mặt phẳng toạ độ (ớ.vy), (ơyz), (ơxz).
b) Lập phương trình của các mặt phẳng đi qua điểm M{2 ; 6 ; -3) và lần lượt song song với các mặt phẳng toạ độ.
Lập phương trình của mặt phảng :
Chứa trục Ox và điểm 5(4 ; -1 ; 2);
Chứa trục Oy và điểm <2(1 ; 4 ; -3);
Chứa trục ơz và điểm 5(3 ; -4 ; 7).
Cho tứ diện có các đỉnh là Â(5 ; 1 ; 3), 5(1; 6 ; 2), C(5 ; 0; 4), 5>(4; 0 ; 6).
Hãy viết phương trình của các mặt phẳng (ÂC5>) và {BCD).
Hãy viết phương trình mặt phẳng (cộ đi qua cạnh AB và song song với cạnh CD.
Hãy viết phương trình mặt phẳng (cộ đi qua điểm M(2 ; -1 ; 2) và song song với mặt phẳng {/3) : 2x - y + 3z + 4 = 0.
Lập phương trình mặt phảng (cộ đi qua hai điểm A( 1 ; 0 ; 1), 5(5 ; 2 ; 3) vằ vuông góc với mặt phảng {/3) : 2x - y + z - 7 = 0.
Xác định các giá trị của m và n để mỗi cặp mặt phẳng sau đây là một cặp mặt phẳng song song với nhau :
2.V + my + 3z - 5 = 0 và	ỈỈX - 8y - 6z + 2 = 0 ;
3x - 5y + mz -3 = 0 và	2.Y + ny - 3z + 1 = 0.
Tính khoảng cách từ điểm Ẩ(2 ; 4 ; -3) lần lượt đến các mặt phẳng sau :
2x - y + 2z - 9 = 0 ;
12.r-5z + 5 = 0;
X = 0.
Giải bài toán sau đây bằng phương pháp toạ độ :
Cho hình lập phương ABCDA'B'C'D' cạnh bằng 1.
Chứng minh rằng hai mặt phẳng (ẨỔ'Z)') và {BCD} song song với nhau.
Tính khoảng cách giữa hai mặt phẳng nói trên.