SGK Hình Học 12 - Bài 2. Khối đa diện lồi và khối đa diện đều

§2. KHỐI ĐA DIỆN LÓI VÀ
KHÔI ĐA DIỆN ĐỀU
KHỐI ĐA DIỆN LỔI
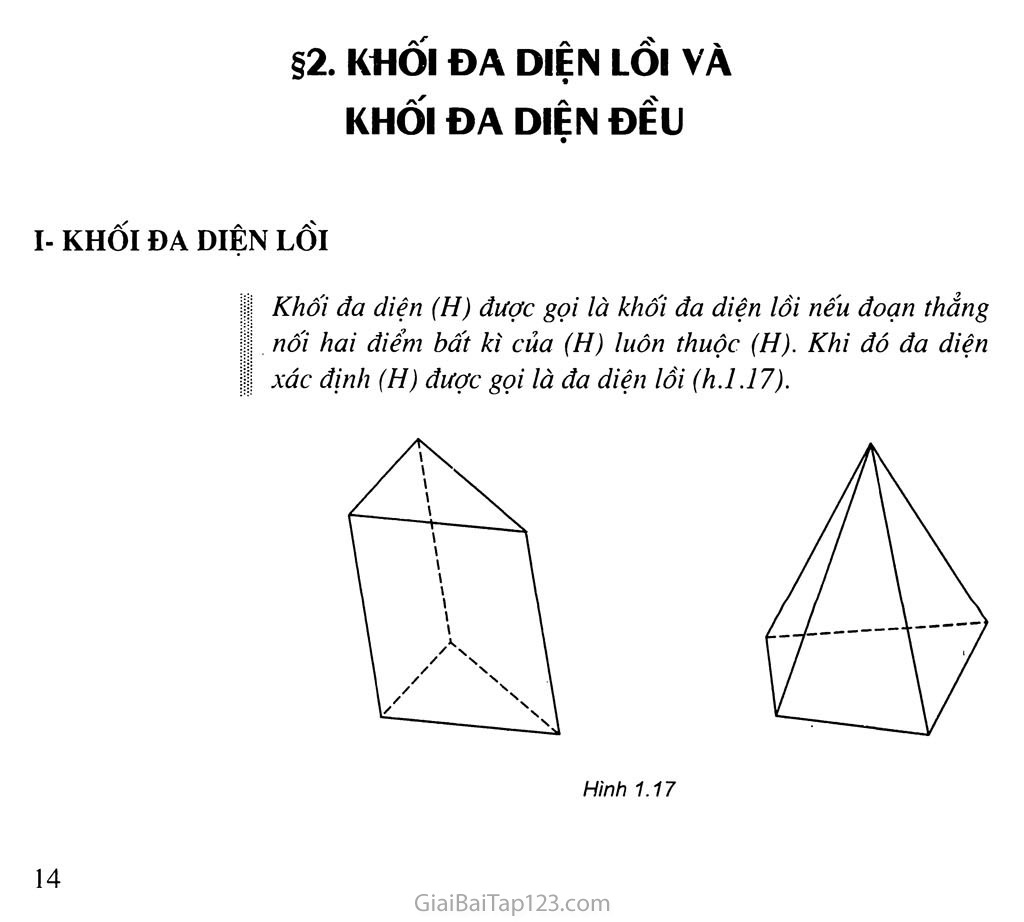
I Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi (h.1.17).
Ví dụ. Các khối lăng trụ tam giác, khối hộp, khối tứ diện là những khối đa diện lồi.
Người ta chứng minh được rằng một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó (h.1.18).
Ai
Tìm ví dụ vế khối đa diện lồi và khối đa diện không lồi trong thực tế.
KHỐI ĐA DIỆN ĐỂU
Quan sát khối tứ diện đều (h.l.l9a), ta thấy các mặt của nó là những tam giác đều, mỗi đỉnh của nó là đỉnh chung của đúng ba mặt. Đối với khối lập phương (h.l.l9b), ta thấy các
. mặt của nó là những hình vuông, mỗi đỉnh của nó là đỉnh chung của đúng ba mặt. Những khối đa diện nói trên được gọi là những khối đa diện đều.
Định nghĩa
I Khối đa diện đều là khối đa diện lồi có tính chất sau đây :
I a) Mỗi mặt của nó là một đa giác đều p cạnh.
I b) Mồi đỉnh của nó là dinh chung của dáng q mặt.
I Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p ; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
Người ta chứng minh được định lí sau :
II Định lí
I Chỉ có năm loại khối đa diện đều. Đó là loại Ị 3 ; 3}, loại {4 ; 3 Ị, 1 loại {3 ; 4}, loại Ị 5 ; 3} và loại {3 ; 5}.
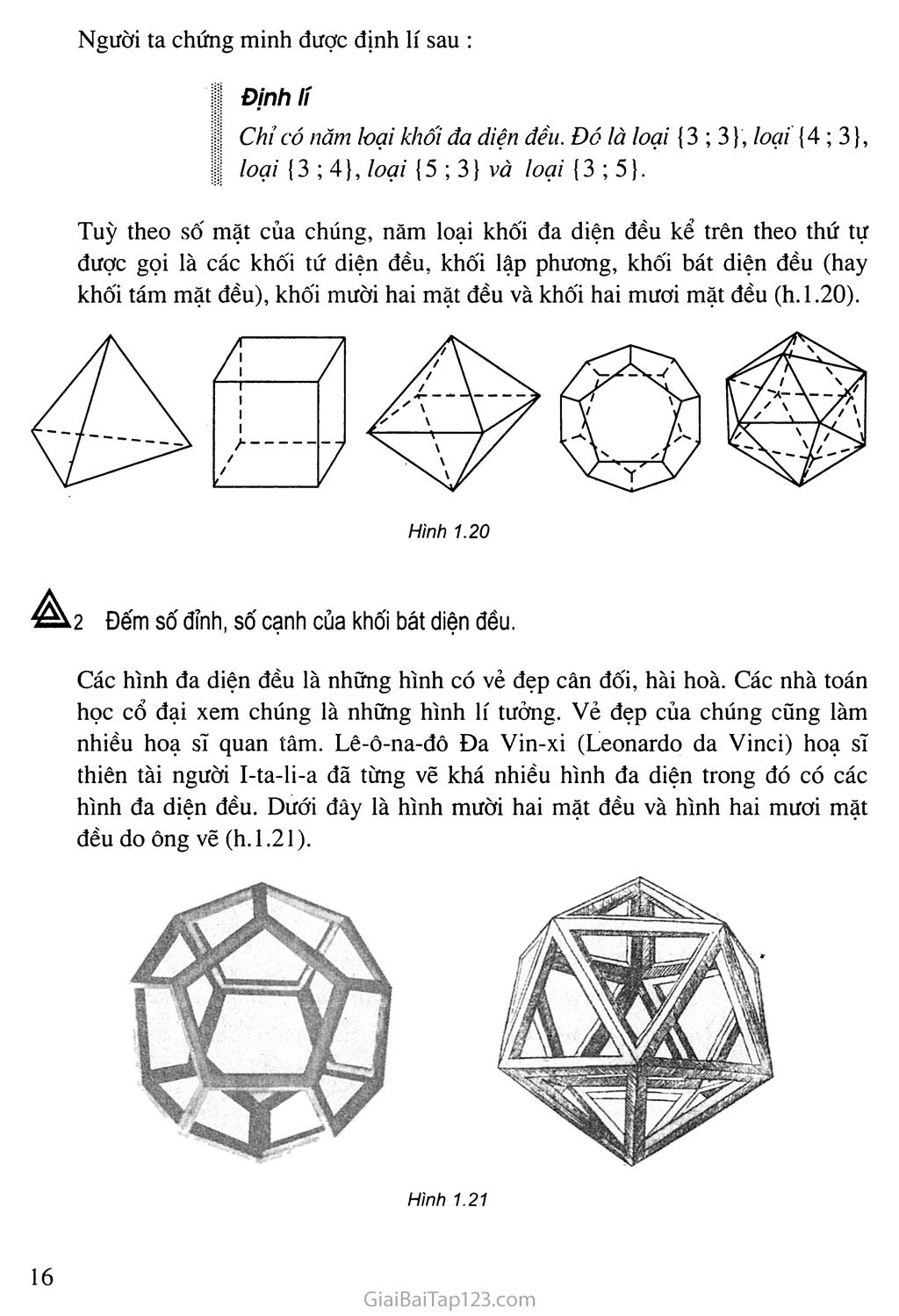
Tuỳ theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự được gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều (h. 1.20).
2 Đếm số đỉnh, số cạnh của khối bát diện đều.
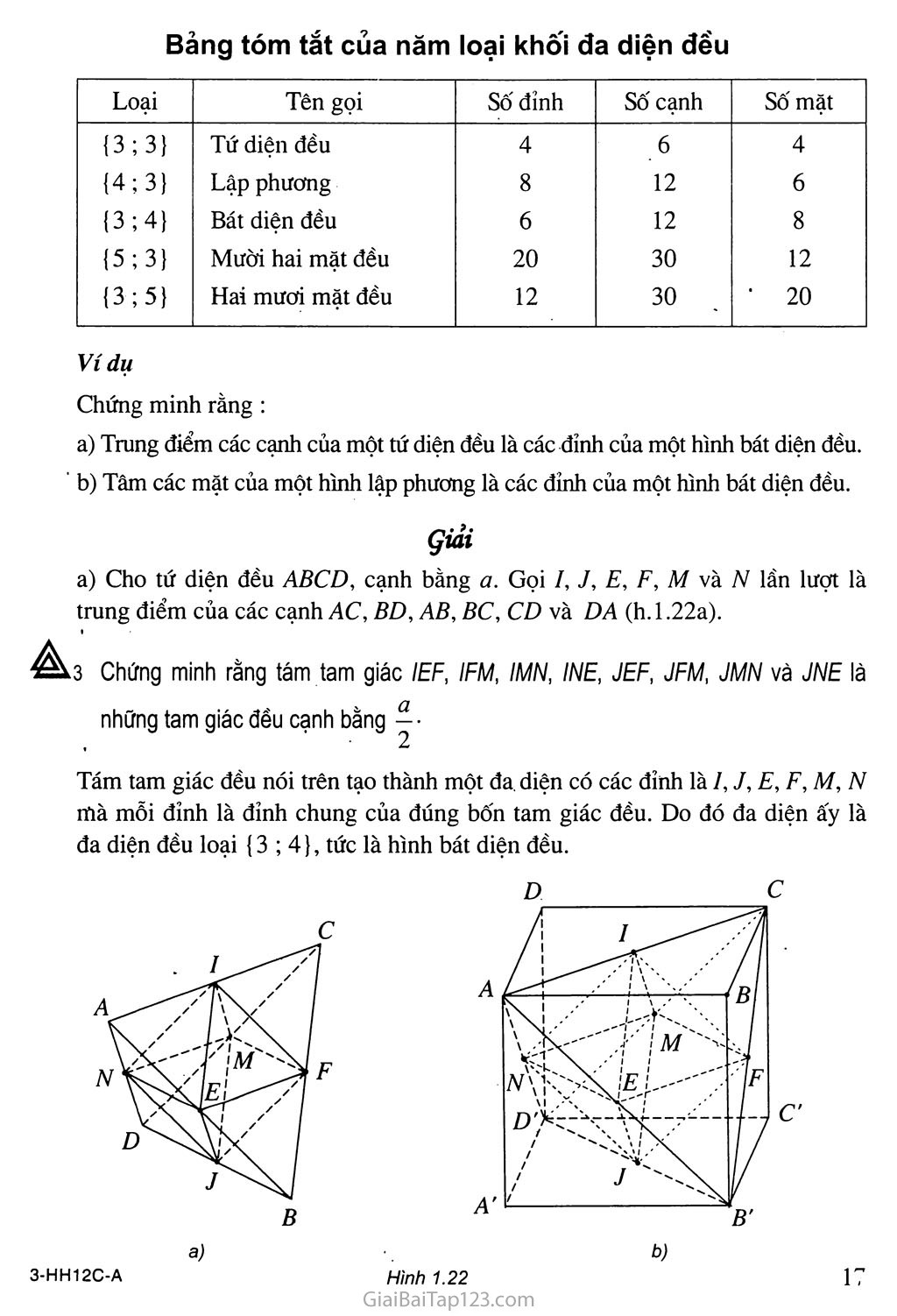
Các hình đa diện đều là những hình có vẻ đẹp cân đối, hài hoà. Các nhà toán học cổ đại xem chúng là những hình lí tưởng, vẻ đẹp của chúng cũng làm nhiều hoạ sĩ quan tâm. Lê-ô-na-đô Đa Vin-xi (Leonardo da Vinci) hoạ sĩ thiên tài người I-ta-li-a đã từng vẽ khá nhiều hình đa diện trong đó có các hình đa diện đều. Dưới đây là hình mười hai mặt đều và hình hai mươi mặt đều do ông vẽ (h. 1.21).
Hình 1.21
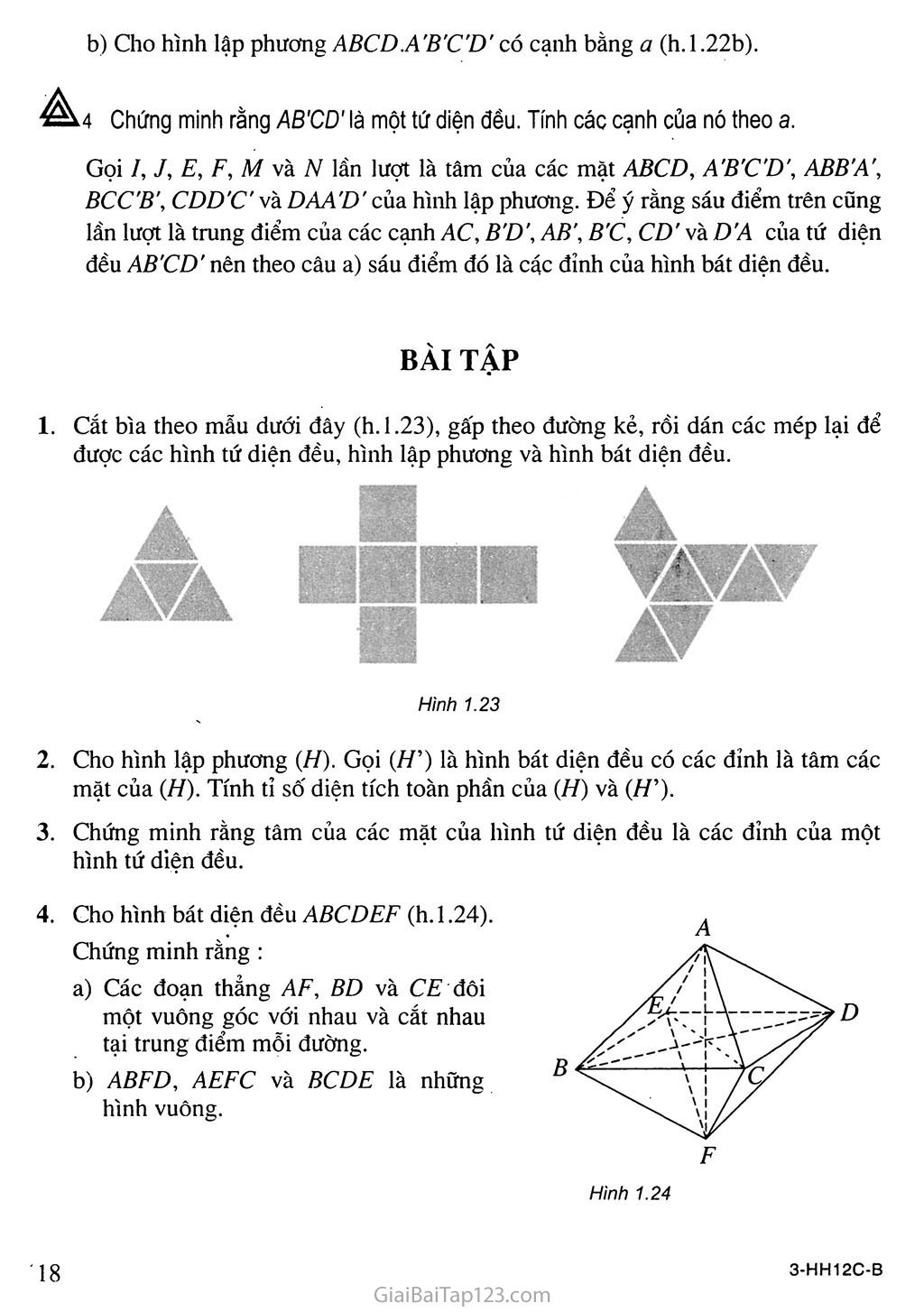
Bảng tóm tắt của năm loại khối đa diện đều
Loại
Tên gọi
Số đỉnh
Số cạnh
Số mặt
{3 ; 3}
Tứ diện đều
4
6
4
{4; 3}
Lập phương
8
12
6
{3; 4}
Bát diện đều
6
12
8
{5 ; 3}
Mười hai mặt đều
20
30
12
{3 ; 5}
Hai mươi mặt đều
12
30
• 20
Ví dụ
Chứng minh rằng :
Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình bát diện đều.
Tâm các mặt của một hình lập phương là các đỉnh của một hình bát diện đều.
ỹiảt'
a) Cho tứ diện đều ABCD, cạnh bằng a. Gọi /, E, F, M và N lần lượt là trung điểm của các cạnh AC, BD, AB, BC, CD và DA (h. 1.22a).
a
2'
^3 Chứng minh rằng tám tam giác IEF, IFM, IMN, INE, JEF, JFM, JMN và JNE là những tam giác đều cạnh bằng
Tám tam giác đều nói trên tạo thành một đa diện có các đỉnh là ỉ, J, E, F, M, N mà mỗi đỉnh là đỉnh chung của đúng bốn tam giác đều. Do đó đa diện ấy là đa diện đều loại {3 ; 4}, tức là hình bát diện đều.
b) Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a (h. 1,22b).
Chứng minh rằng AB'CD' là một tứ diện đều. Tính các cạnh của nó theo a.
Gọi ỉ, J, E, F, M và N lần lượt là tâm của các mặt ABCD, A'B'C'D', ABB'A', BCC'B', CDD'C' và DAA'D' của hình lập phương. Để ý rằng sáu điểm trên cũng lần lượt là trung điểm của các cạnh AC, B'D', AB', B'C, CD' và D'A của tứ diện đều AB'CD' nên theo câu a) sáu điểm đó là cạc đỉnh của hình bát diện đều.
BÀI TẬP
Cắt bìa theo mẫu dưới đây (h. 1.23), gấp theo đường kẻ, rồi dán các mép lại để
được các hình tứ diện đều, hình lập phương và hình bát diện đều.
Hình 1.23
Cho hình lập phương (//). Gọi (//’) là hình bát diện đều có các đỉnh là tâm các mặt của (//). Tính tỉ số diện tích toàn phần của (//) và (//’).
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
Hình 1.24
Cho hình bát diện đều ABCDEF (h. 1.24).
Chứng minh rằng :
Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
ABFD, AEFC và BCDE là những hình vuông.
Tjinh đa diện đều
Câu chuyện về các hình đa diện đều mang nhiều tính huyền thoại. Người ta không biết được ai là người đầu tiên đã tìm ra chúng. Trong một cuộc khai quật, người ta đã tìm thấy một thứ đồ chơi của trẻ em có hình hai mươi mặt đều với niên đại cách chúng ta khoảng 2500 năm. Các nhà toán học cổ đại Hi Lạp thuộc trường phái Pla-tông và trước đó nữa là trường phái Py-ta-go (thế kỉ IV trước Công nguyên) đã từng nghiên cứu về các hình đa diện nói chung và các hình đa diện đều nói riêng. Các nhà toán học thời bấy giờ coi năm loại hình đa diện đều là những hình lí tưởng. Người ta coỉ bốn loại đa diện đều dễ dựng là tứ diện, hình lập phương, hình bát diện đều và hình hai mươi mặt đều, theo thứ tự tượng trưng cho lửa, đất, không khí và nước, đó là bốn yếu tố cơ bản (theo quan niệm của thời bấy giờ) tạo nên mọi vật. Còn hình mười hai mặt đều tượng trung cho toàn thể vũ trụ.
Không khí	Nước
Sau này người ta còn tìm thấy các hình đa diện đều xuất hiện trong tự nhiên dưới dạng tinh thể của nhiều hợp chất. Chẳng hạn tinh thể của các chất sodium sulphantimoniate, muối ăn, chrome alum có dạng tương ứng là khối tứ diện, khối lập phương, khối bát diện đều. Còn hai loại hình đa diện đều phức tạp hơn là hình mười hai mặt đều và hĩnh hai mươi mặt đều, xuất hiện
trong khung xương của một số vi sinh vật biển ví dụ : circogonia icosahedra và circorrhegma dodecahedra. *	•
Các hình đa diện đều là những hình có tâm, trục hoặc mặt phẳng đối xứng. Việc nghiên cứu các phép biến hình biến mỗi hình đa diện đều thành chính nó đã đặt nền móng cho lí thuyết về các nhóm hữu hạn, một hướng nghiên cứu quan trọng của đại số. Lí thuyết này có nhiều ứng dụng trong việc nghiên cứu các dạng tinh thể của các hợp chất hoá học.