Giải bài tập Toán 10 Bài 2. Tổng và hiệu của hai vectơ

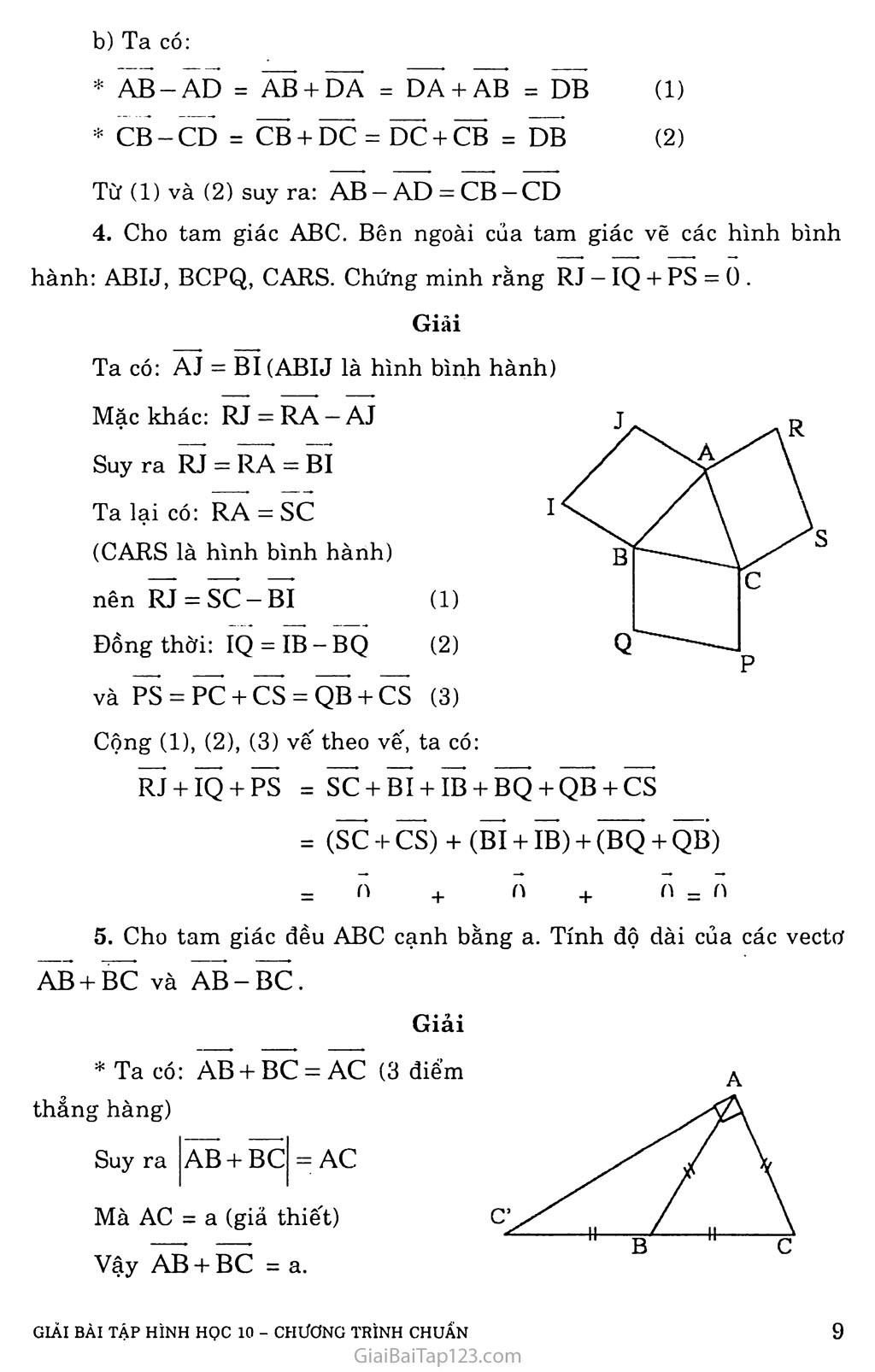
BÀI 2. TỔNG VÀ HIỆU CỦA HAI VECTƠ
A. KIẾN THỨC CẨN NAM vững
Tống của hai vectơ
Cho hai vecto’ ã, b và điểm A tùy ý. Vẽ AB = a và BC = b.
Ta có AC là tổng của hai vectơ ạ và b, kí hiệu: AC = a + b
Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì ÃB + Ã15 = Ãc.
Tính chất
Cho ba vectơ a, b, c tùy ý, ta có:
- a + b = b + a (tính chất giao hoán)
— a+0-0+a-a
tính chất của 0
a+b+c = a+b + c (tính chất kết hợp)
Hiệu của hai vectơ
Cho vectơ a. Vectơ có cùng độ dài và ngược hướng với a được gọi là vectơ đối của a. Kí hiệu: —a
Cho hai vectơ a và b. Hiệu của a và b là a + (- b).
Ký hiệu: a - b
Mở rộng
Nếu I là trung điểm của đoạn thẳng AB thì IA + IB = 0
Nếu G là trọng tâm của AABC thì GA + GB + GC = Õ
B. GIẢI BÀI TẬP
Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vectơ MA + MB và MA — MB.
Giải
* Vectơ MA + MB
~Ã C
Trên đoạn MA, lấy điểm c sao cho AC = MB.
Khi đó MÃ + MB = MÃ + Ãc.
Theo quy tắc ba điểm, ta có: MA + MB = MC.
(vì MA > MB nên c thuộc đoạn AM).
Vectơ MA —MB
Ta có MA —MB = MA + (—MB)
= MA + BM = BM + MA (tính giao hoán)
- BA (quy tắc ba điểm)
Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh
(1)
rằng MA + MC = MB + MD .
Giải
Gọi o là tâm của hình bình hành đã cho. Ta có OA = oc và OB = OD
Gọi M’ là điểm đôi xứng của M qua 0. Ta có:
- AMCM’ là hình bình hành. Theo quy tắc hình bình hành thì: '
MA + MC = MM'
- BMDM’ là hình bình hành. Theo quy tắc hình bình hành thì:
MB + MD = MM'	(2)
Từ (1) và (2) suy ra: MA + MC = MB + MD
Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
a) AB + BC + CD + DA = õ b) AB - AD = CB - CD .
Giải
a) Ta có: AB+ BC + CD + DA = (AB + BC) + (CB + DA)
= AC + CA = AA = 0
b) Ta có:
AB-AD = AB + DA = DA + AB = DB	(1)
CB-CD = CB + DC = DC + CB = DB	(2)
Từ (1) và (2) suy ra: AB-AD = CB-CD
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành: ABIJ, BCPQ, CARS. Chứng minh rằng RJ — IQ + PS = 0 .
Giải
Ta có: AJ = BI (ABIJ là hình bình hành)
Mặc khác: RJ = RA —AJ
Suy ra RJ = RA = BI
Ta lại có: RA = sc
(CARS là hình bình hành) nên RJ = SC —BI	(1)
Đồng thời: IQ = IB-BQ (2) và PS = PC + CS = QB + CS (3) Cộng (1), (2), (3) vế theo vế, ta có:
RJ + IQ + PS = SC + BI + IB + BQ + QB + CS
= (SC + CS) + (BI + IB) + (BQ + QB)
n + n + n = n
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ AB + BC và AB — BC.
Giải
Suy ra AB + BC = AC
* Ta có: AB + BC = AC (3 điểm thẳng hàng)
Mà AC = a (giả thiết)
Vậy AB + BC = a.
* Ta có: AB - BC = AB + (-BC) (*)
Gọi C’ là điểm đối xứng của 0 qua B, ta có: BC' = -BC
Khi đó (*) o AB- BC = AB + Bơ
=> AB-BC
Xét A ACC’, ta có trung tuyến AB bằng nửa cạnh tương ứng CC’ nên vuông tại A. Suy ra AC’ = Vcc2 — AC2 = aVs
Vậy AB - BC = Vã
AB-BC = DB ; DA - DB + DC = õ .
Cho hình bình hành ABCD có tâm o. Chứng minh rằng:
a) CO - OB = BA ;	b)
DA - DB = OA - OB :	d)
A	B
D	c
Giải
Ta có: CD = BA (ABCD là hình
bình hành) (1)
Mặc khác: BO-OD (0 là trung điểm của BD)
Khi đó co - OB = co + ÕĨ5 = CD (2)
Từ (1) và (2) suy ra co - OB = BA
Ta có: DA = -BC (ABCD là hình bình hành)
Mà AB-BC = AB + (-BC) = AB + DA = DA + AB = DB
Vậy AB-BC=DB
c) Ta có:
DA - DB = BA (quy tắc ba điểm)
Mà
BA = OA - OB (quy tắc ba điểm)
Vậy
DÃ - DB = ÕẨ - OB
d) Ta có: DA - DB = BA (quy tắc ba điểm)
Mà
BA = -DC nên BA + DC = 0
Suy ra
DA - DB + DC = DA - BD + CD = BA + CD = 0
Vậy
DA - DB + DC = õ.
Cho a, b là hai vectơ khác 0. Khi nào có đẳng thức:
a) a + b = a + b ;
b) a + b = a - b
Giải
a) Đặt a = AB và b = BC
Giả sử a và b cùng hướng thì A, B, c thẳng hàng, ta có:
a+b=AB+BC=AC
a + b = AB + AC = AC
Từ (1) và (2) suy ra a + b = a + b
Vậy a + b = a + b khi a và b là hai vectơ cùng hướng
b) Đặt a = AB và b = BC
Giả sử A ABC vuông tại B, ta có:
của hình chữ nhật
* a + b = AB + BC = BD (D là đỉnh thứ tư
ABCD)
A
a-b = AB-BC = AB + (-BC)
Gọi C’ là điểm đối xứng của c qua B, ta có:
a - b = AB + Bố' = Bly (D là
đỉnh thứ tư của hình chữ nhật ABC’D’)	/
\ a + b
* Do đó:
a - b /
•
a + b
= BD	/
a \
•
a - b
= BU'	C’ 't
-b
-b
Mà BD = BD’ nên a 4- b = a - b
Vậy a + b = a — b khi a vuông góc với b .
Cho a + b = 0 . So sánh độ dài, phương và hướng của hai vectơ
Giải
Vì
a + b = 0 nên a 4- b = 0,
suy ra a = - b
Vậy a và b là hai vecto' cùng phương, có cùng độ lớn và ngược chiều nhau.
Chứng minh rằng AB = CD khi và chỉ khi khi trung điểm của hai đoạn thắng AD và BC trùng nhau.
Giai
Nêu AB = CD thì ABCD là hình bình hành. Khi đó AD và BC có trung điếm trùng nhau.
Nêu AD và BC có trung điểm trùng nhau thì ABCD là hình bình hành. Khi đó AB - CD .
Cho ba lực F| = MA, F? = MB, và Fl = BC cùng tác động vào một vật tại điếm M và vật đứng yên. Cho biết cường độ của F|,F? đều là 100N và AMB = 60°. Tìm cường độ và hướng của lực F.I.
Giải
* Xét AAMC ta có: MA = MB = 100N A	c
Vì F1 là lực tống hợp của F| và F?
nên: F3 = MC với MC = MA 4- MB
Suy ra F3 có cường độ bằng MC và F3 có hướng là tia phân giác trong của AMB.
Vì AMBC là hình thoi nên MC = 2MH.
Do đó MC = lOOx/ã (N)
Vậy F3 — I00V3 (N) và có hướng là tia phân giác trong của AMB .