Giải bài tập Toán 10 Bài 3. Hệ thức lượng trong tam giác và giải tam giác
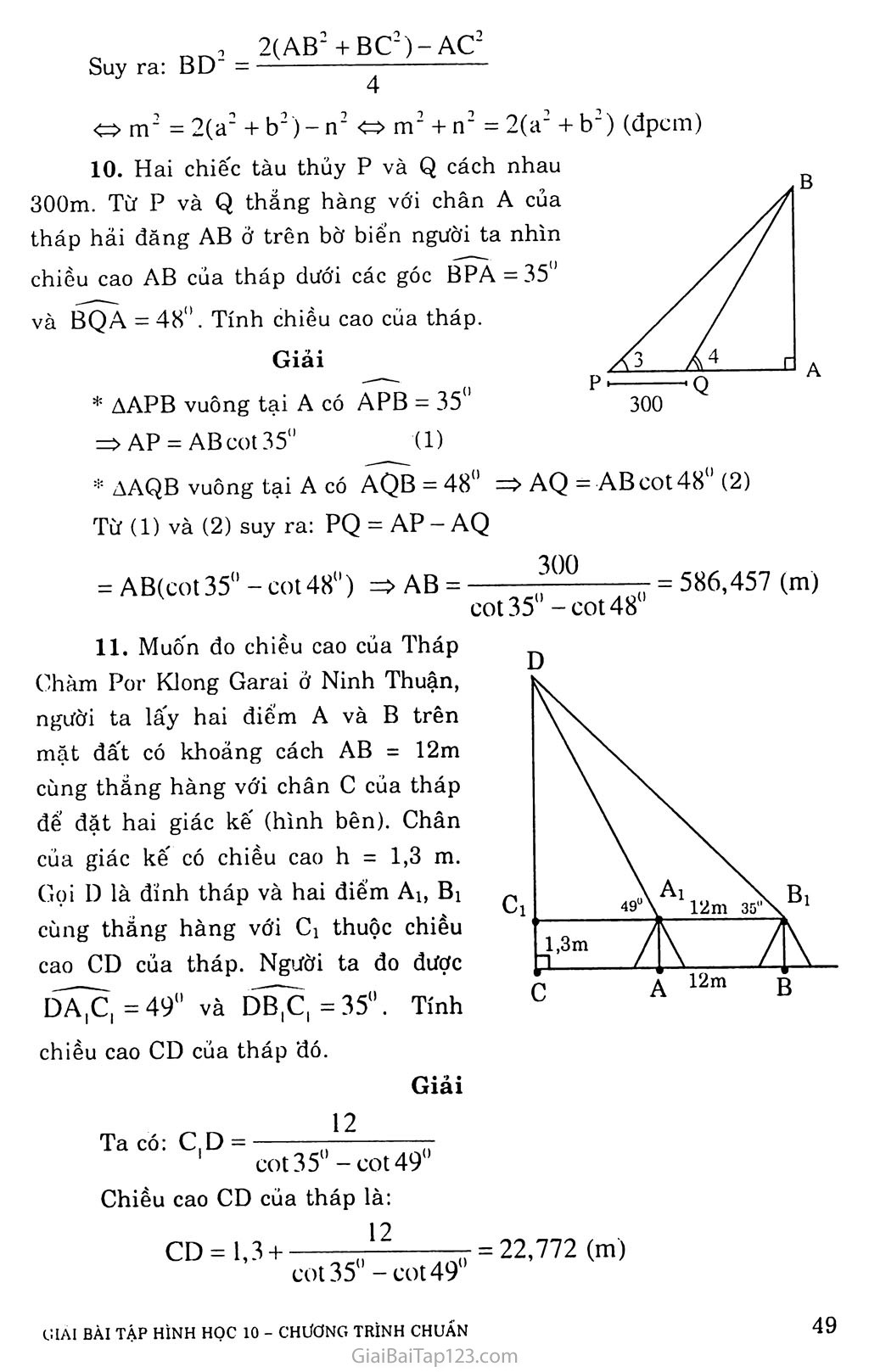
BÀI 3. HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GlẢl TAM GIÁC A. KIẾN THỨC CẦN NAM vững Định lí cosin Cho AABC có BC = a, CA = b, AB = c, khi đó: a2 = b2 + c2 - 2bc cosA b2 = a2 + c2 - 2ca cosB c2 - a2 + b2 - 2ab cosC Hộ thức giữa cạnh và trung tuyến của tam giác: 2 2(b2+c2)-a2 c 4 Định lí sin Cho AABC có BC = a, CA = b, AB = c, khi đó: -A- = ^- = ^- = 2R sinA sinB sinC (R là bán kính đường tròn ngoại tiếp AABC). Diện tích tam giác r là bán kính đường Giải * Ta có: C = 90° - B = 90"-58° = 32° Vậy c = 32° Ta có: b = BCsin58" Tính ra ta được b = 61,06(cm) Ta có: c = BCcos58" Tính ra ta được c = 38,15(cm) AB.AC 38,15.61,06 , * Ta có: ha = — = 32,35(cm) BC 72 2. Cho tam giác ABC biết các cạnh a = 52,lcm, b - 85cm, c - 54cm. Tính các góc A, B và c. Giải , + b + c - a Ta có: cosA = A —_ 2bc Vậy A - 36" Ta có: cosB = + d — 2ac 2.85.54 542 + 52, l2 -852 2.52,1.54 Vậy B = 106"28 , - _a2 + b2-c2 * Ta có: cosC = — 2ab 2.52,1.85 Vậy C = 37°32 3. Cho tam giác ABC có A - 120°, cạnh b = 8 cm và c = 5 cm. Tính cạnh a, và các góc B , c của tam giác đó. Giải * Ta có: a2 = b2 + c2 - 2bc cos A = 82 + 52 -2.8.5COS 120" = 64 + 25 +8oị = 129 2 Vậy a = V129 = 11,36 (em) * Ta có: si nA => sinB Tính ra ta được sinB bsinA _ k’ 2 _ 4^3 a = 11,36 = 11.36 B = 37°34 * Ta CÓ: c = 1801’-(A + B) = 180°-(120°+37°34) = 22°26 Tính diện tích s của tam giác có số đo các cạnh lần lượt là 7, 9 và 12. Giải a+ b + c 7 + 9+12 Ta CÓ: p = —— = — 14 2 2 p - a = 7; p - b = 5; p - C = 2. Vậy s = ựp(p-a)(p-b)(p-c) = 714.7.5.2 = 7.2.V5 = 14^/5 =31,3 (đơn vị diện tích) Tam giác ABC có A = 120” . Tính cạnh BC, cho biết cạnh AC = m và AB = n. Giải Ta có: BC2 = m2 + n2 -2m.n.cosl20(l = m2 + n2 + mn => BC = 7m3 4- n’ + m.n Tam giác ABC có các cạnh a = 8cm, b - 10 cm và c = 13 cm. Tam giác đó có góc tù không? Tính độ dài trung tuyến MA của tam giác ABC đó. Giải A a2 + b2-c2 82 + 102 - 132 164-169.m a) 1 a có: cosC = — = = —:——— < 0 2ab 2.8.10 160 Vậy trong tam giác có c là góc tù. ,.Tq nA" m2 _ 2(b2+ c2)-a2 2(102 + 132)- 82 . b) Ta có: m — = — = 118,5 a 4 4 Vậy ma =10,9 (em) Tính góc lớn nhất của ABC biết: Các cạnh a = 3 cm, b = 4 cm và c = 6 cm; Các cạnh a = 40cm, b = 13 cm và c = 37 cm Giải Cạnh c - 6 (cm) lớn nhất suy ra c là góc lớn nhất. 2, a2 + b2-c2 9 + 16-36 -11 cos c = — = ———— = —— 2ab 2.3.4 24 Vậy c = 117° 16 b) Cạnh a = 40 (cm) lớn nhất suy ra A là góc lớn nhất 7 b2 + c2-a2 cos A = — = 2bc 132 +372 -402 t\í\íZAA = — = -0,0644 2.13.37 Vậy Ẵ = 93°4Í Cho tam giác ABC biết cạnh a = 137,5cm, B - 83" và c = 57° . Tính A , bán kính R của đường tròn ngoại tiếp, cạnh b và c của tạm giác. Giải * Ta có: Ấ = 180" -(83" + 57") = 40" , b a asinB 137.5.sin83" * Ta có: = —— b = - = —— và BD. Khi đó o là trung điểm của sinB sin A sin A sin 40" Vậy b = 212,3 (cm) * Ta có: —=> c = sinC sin A Vậy c = 179,4 (em) Cho hình bình hành ABCD có AB = a, BC = b, BD = m và AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2). Giải Gọi o là giao điểm của AC AC và BD, đồng thời BO là trung tuyến của AABC. Q..., rQ. Rn2 2(AB2 + BC2)-AC2 Suy ra: BD =— 4 m2 = 2(a2 + b2) - n2 m2 + n2 = 2(a2 + b2) (đpcm) Hai chiếc tàu thủy p và Q cách nhau 300m. Từ p và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc BPA = 35" và BQA = 48". Tính chiều cao của tháp. Giải AAPB vuông tại A có APB = 35" =>AP = ABcot35" (1) = AB(cot35"-cot48") => AB = 300 _= 586,457 (m) CO135 -CO148 Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12m cùng thẳng hàng với chân c của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3 m. Gọi I) là đinh tháp và hai điếm Al, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được DA^C, = 49° và DB^C, = 35". Tính chiều cao CD của tháp đó. Giải Ta có: C,D = 12 C0t35" - C0t49" AAQB vuông tại A có AQB = 48" => AQ = AB cot 48" (2) Từ (1) và (2) suy ra: PQ = AP - AQ Chiều cao CD của tháp là: 12 CD = 1,3+ CO135 -cot49 = 22,772 (m)