SGK Toán 9 - Bài 4. Công thức nghiệm của phương trình bậc hai
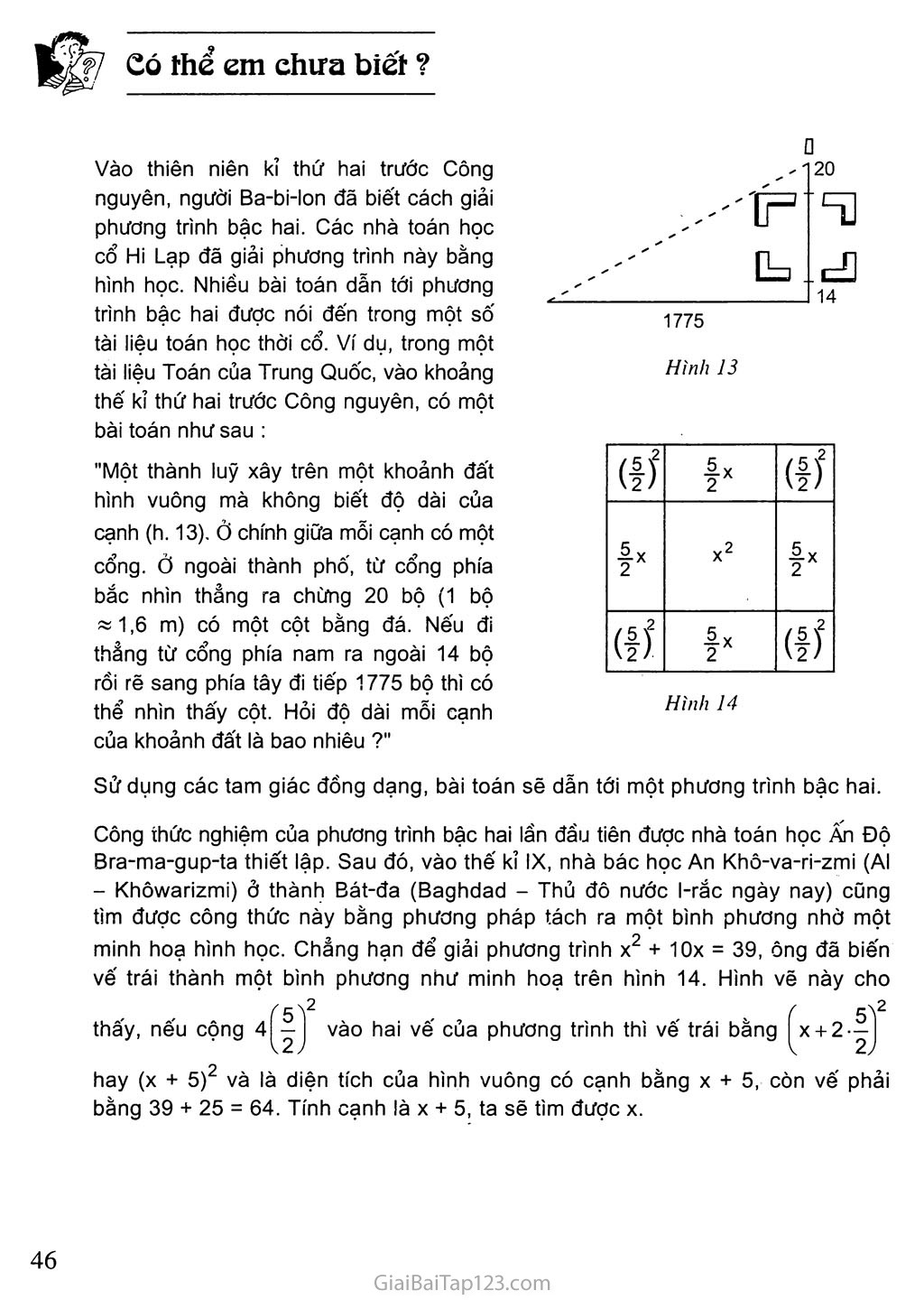
§4. Công ỉhức nghiệm của phương ỉrình bậc hai Trong mục này, ta sẽ xét xem khi nào phương trình bậc hai có nghiệm và tìm công thức nghiệm khi phương trình có nghiệm. Công thức nghiệm Biến đổi phương trình tổng quát ax2 + bx + c = 0 (a 0) (1) theo các bước như khi giải phương trình 2x2 - 8x + 1 = 0 ở ví dụ 3 (§3). - Chuyển hạng tử tự do sang vế phải : ax2 + bx = -c. c - Tách hạng tử — X thành 2.x.^— và thêm vào hai vế cùng một biểu thức a 2a để vế trái thành bình phương của một biểu thức : ta được c a b Áp dụng Ví dụ. Giải phương trình 3x + 5x - 1 = 0. - 4ac 4a2 hay ' . \2 è] (2) Người ta kí hiệu A = b - 4ac và gọi nó là biệt thức của phương trình (A là một chữ cái Hi Lạp, đọc là "đenta"). Bây giờ dùng phương trình (2), ta xét mọi trường hợp có thể xảy ra đối với A để suy ra khi nào thì phương trình có nghiệm và viết nghiệm nếu có. UI Hãy điền những biểu thức thích hợp vào các chỗ trống (...) dưới đây : X + ^L = ± ... 2a Xo = Nếu A > 0 í/ừ từ phương trình (2) suy ra Do đó, phương trình (1) có hai nghiệm : 2a Nếu A = 0 thì từ phương trình (2) suy ra Do đó, phương trình (1) cớ nghiệm kép X = m Hãy giải thích vì sao khi A < 0 thì phương trình vô nghiệm. Tóm lại, ta có kết luận chung sau đây. Đối với phương trình ax2 + bx + c = 0 (a 0) và biệt thức A = b2 - 4ac : Nếu A > 0 thì phương trình có hai nghiêm phân biệt: -b + VÃ -b - VÃ Xl= 2T^’X2= 2T^; Nếu A = 0 thì phương trình có nghiệm kép Xị = x2 = “V— ; Za Nếu A < 0 thì phương trình vô nghiệm. Giải Tính A = b2 - 4ac. Phương trình có các hệ số là a = 3, b = 5, c = -1. A = 52 - 4.3 . (-1) = 25 + 12 = 37. Do A > 0, áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt: -5 + 737 -5-737 x' X2= —6 • Áp dụng công thức nghiêm để giải các phương trình : a) 5x2 - X + 2 = 0 ; b) 4x2 - 4x + 1 = 0 ; -3x2 + X + 5 = 0. Chú ý. Nếu phương trình ax2 + bx + c = 0 (a 0) có a và c trái dấu, tức là ac 0. Khi đó, phương trình có hai nghiệm phân biệt. Bài tập Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức A và xác định số nghiệm của mỗi phương trình sau : a) 7x2 - 2x + 3 = 0 ; b) 5x2 + 2Vĩõx + 2 = 0 ; c) | x2 + 7x + I = 0; d) l,7x2- l,2x-2,l =0. Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau : a) 2xz - 7x + 3 = 0 ; 6x“ + X + 5 = 0 ; 6xz + X - 5 = 0 ; 3x“ + 5x + 2 = 0 ; y - 8y + 16 = 0 ; 16z2 + 24z + 9 = 0. Có thể em ehưa biết ? Vào thiên niên kỉ thứ hai trước Công nguyên, người Ba-bi-lon đã biết cách giải phương trình bậc hai. Các nhà toán học cổ Hi Lạp đã giải phương trình này bằng hình học. Nhiều bài toán dẫn tới phương trình bậc hai được nói đến trong một số tài liệu toán học thời cổ. Ví dụ, trong một tài liệu Toán của Trung Quốc, vào khoảng thế kỉ thứ hai trước Công nguyên, có một bài toán như sau : "Một thành luỹ xây trên một khoảnh đất hình vuông mà không biết độ dài của cạnh (h. 13). Ở chính giữa mỗi cạnh có một cổng. Ở ngoài thành phố, từ cổng phía bắc nhìn thẳng ra chừng 20 bộ (1 bộ «1,6 m) có một cột bằng đá. Nếu đi thẳng từ cổng phía nam ra ngoài 14 bộ rồi rẽ sang phía tây đi tiếp 1775 bộ thì có thể nhìn thấy cột. Hỏi độ dài mỗi cạnh của khoảnh đất là bao nhiêu ?" (I)2 ỉx (ỉí X2 K5|Ư1 X <iỉ í’ (ị)2 ũ Hình 13 Hình 14 Sử dụng các tam giác đồng dạng, bài toán sẽ dẫn tới một phương trình bậc hai. Công thức nghiệm của phương trình bậc hai lần đầu tiên được nhà toán học Ấn Độ Bra-ma-gup-ta thiết lập. Sau đó, vào thế kỉ IX, nhà bác học An Khô-va-ri-zmi (AI - Khowarizmi) ở thành Bát-đa (Baghdad - Thủ đô nước l-rắc ngày nay) cũng tìm được công thức này bằng phương pháp tách ra một bình phương nhờ một minh hoạ hình học. Chẳng hạn để giải phương trình X2 + 10x = 39, ông đã biến vế trái thành một bình phương như minh hoạ trên hình 14. Hình vẽ này cho thấy, nếu cộng 4^-| j vào hai vế của phương trình thì vế trái bằng ^x + 2-|^ hay (x + 5)2 và là diện tích của hình vuông có cạnh bằng X + 5, còn vế phải bằng 39 + 25 = 64. Tính cạnh là X + 5, ta sẽ tìm được X. Bài đọc thêm GIẢI PHƯƠNG TRÌNH BẬC HAI BẰNG MÁY TÍNH BỎ TÚI CASIO fx-220 Tính A = b2 - 4ac. Nếu A < 0 thì phương trình vô nghiệm. Nếu A > 0, ta tìm nghiệm. Vì VÃ được dùng hai lần nên ta dùng phím nhớ Min lưu nó lại trong máy rồi tìm các nghiệm. Ví dụ. Giải phương trình 3x2 - 4x - 7 = 0. • Tính A 4 + /- SHIFT X2 — 4 X 3 X 7 +/- = (Máy cho kết quả là 100, vì 100 > 0 nên ta thực hiện tiếp việc tìm nghiệm). ° Tìm nghiệm Min + 4 = 4- 2 4- 3 — Kết quả Xj « 2,333333333. Để tính x2 = 4 Q-’g— ’ta dùng phím I MR 1 để gọi VÃ. Cụ thể : — MR = 4- 6 = Kết quả x2 = -1.