Giải bài tập Toán 12 Bài 1. Khái niệm về khối đa diện

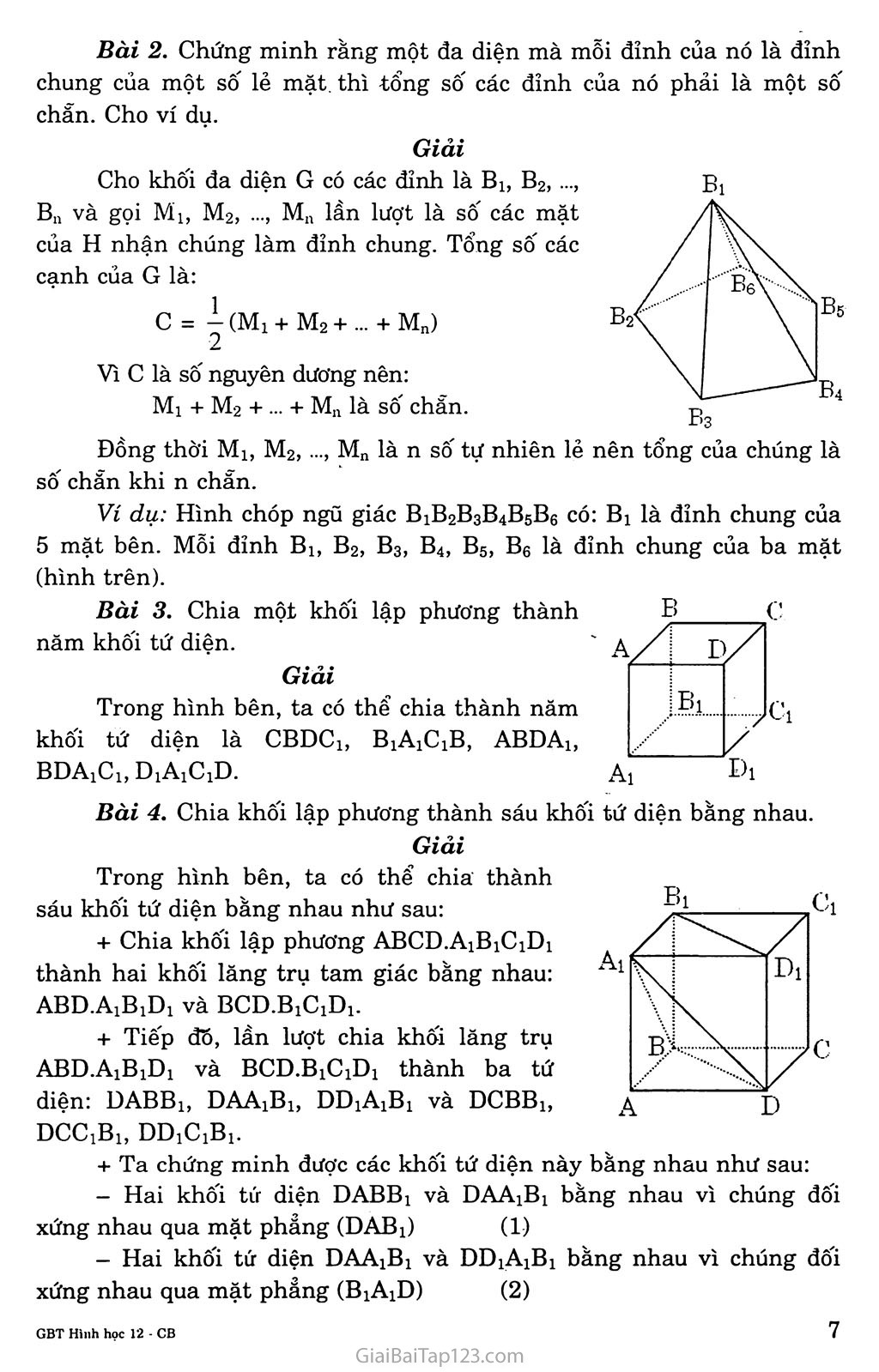
Chương I. KHÔÌ ĐA DIỆN
Bài 1. KHÁI NIỆM VỀ KHÔÌ ĐA DIỆN
A. KIẾN THỨC CẦN NAM vững
HÌNH ĐA DIỆN VÀ KHÔÌ ĐA DIỆN
Hình đa diện
Hình đa diện là một hình trong không gian thỏa mãn:
Gồm một số hữu hạn các đa giác
Hai đa giác khác nhau chỉ có thế hoặc không có điểm chung, hoặc chỉ có duy nhất một đỉnh chung, hoặc chỉ có đúng một cạnh chung.
Mỗi cạnh của một đa giác bất kì đều là cạnh chung của đúng hai đa giác.
Khôi đa diện
Phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó gọi là khối đa diện.
Khối đa diện được gọi là khối chóp (khối lăng trụ, khối hộp,...) nếu khối đa diện đó được giới hạn bởi một hình chóp (hình lăng trụ, hình hộp,...).
Mọi khối đa diện có thể phân chia thành các khối tứ diện và ngược lại, ta có thể ghép hai hoặc nhiều khối tứ diện thành một khối đa diện.
II. HAI KHỐI ĐA DIỆN BANG NHAU
Phép đối xứng qua mặt phẳng và mặt phẳng đối xứng của một hình
* Phép đối xứng qua mặt phảng là phép biến hình biến mỗi điểm thuộc mặt phảng thành chính nó và biến mỗi điểm không thuộc mặt phẳng thành điểm đối xứng với nó qua mặt phẳng.
Định lí: Nếu phép đối xứng qua mp(a) biến hai điểm A, B thành hai điểm A’, B’ thì A’B’ = AB.
Nếu phép đối xứng qua mp(a) biến hình H thành chính nó thì mp(a) gọi là mặt phẳng đôi xứng của hình H.
Phép dời hình
Phép dời hình là phép biến hình trong không gian không làm thay đổi khoảng cách giữa hai điểm bất kì (nghĩa là nếu phép biến hình biến hai điểm bất kì A, B lần lượt thành hai điểm A’, B’ thì A’B’ = AB).
Tính chất
Phép dời hình biến đường thẳng thành đường thẳng, mặt phảng thành mặt phẳng.
Thực hiện liên tiếp các phép dời hình ta sẽ được một phép dời hình.
Các phép dời hỉnh
Phép đối xứng qua mặt phẳng (phần 1)
Phép tịnh tiến: Phép tịnh tiến theo vectơ u là phép biến hình biến mỗi điểm A thành điểm B sao cho AB = u
Phép đối xứng qua đường thẳng: Phép đối xứng qua đường thẳng A là phép biến hình biến mỗi điểm thuộc A thành chính nó và biến mỗi điểm A không thuộc A thành điểm A’ sao cho A là đường trung trực của đoạn thẳng AA’.
Phép đối xứng qua một điểm: Phép đối xứng qua điểm I là phép biến hình biến điểm I thành chính nó và biến mỗi điểm A *1 thành điểm A’ sao cho I là trung điểm của đoạn thẳng AA’.
Hai hình bằng nhau
Nếu có một phép dời hình biến hình này thành hình kia thì hai hình đó bằng nhau.
Định lí: Hai hình tứ diện bằng nhau nếu chúng có các cạnh tương ứng bằng nhau.
B. GIẢI BÀI TẬP
Bài 1. Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn. Cho ví dụ.
Giải
Gọi a là số cạnh, b là số mặt của khối đa diện.
Nếu khối đa diện có các mặt là tam giác thì mỗi mặt có ba cạnh. Trong ba cạnh đó mỗi cạnh lần lượt là cạnh chung của hai mặt.
Ta có 3b = 2a. Nghĩa là b chẵn.
A
Hình 1
Hình 1: 6 cạnh và 4 mặt;
* Ví dụ: hình 1, 2.
Hình 2
2: 9 cạnh và 6 mặt.
Bài 2. Chứng minh rằng một đa diện mà mỗi đỉnh của nó là đỉnh chung của một số lẻ mặt. thì tổng số các đỉnh của nó phải là một số chẵn. Cho ví dụ.
Giải
Cho khối đa diện G có các đỉnh là Bb B2, Bn và gọi Ml, M2, Mn lần lượt là số các mặt của H nhận chúng làm đỉnh chung. Tổng số các cạnh của G là:
c = ị (Ml + M2 + ... + Mn)
2
Vì c là số nguyên dương nên:
Ml + M2 + ... + Mn là số chẵn.
Đồng thời Ml, M2, ..., Mn là n số tự nhiên lẻ nên tổng của chúng là số chẵn khi n chẵn.
Ví dụ: Hình chóp ngũ giác B1B2B3B4B5B6 có: B1 là đỉnh chung của
5 mặt bên. Mỗi đỉnh B1, B2, B3, B4, B5, B6 là đỉnh chung của ba mặt
(hình trên).
Bài 3. Chia một khối lập phương thành năm khối tứ diện.
Giải
Trong hình bên, ta có thể chia thành năm khôi tứ diện là CBDC1, BiAiCiB, ABDA1, BDA1C1, DpÃiCiD.
Bài 4. Chia khối lập phương thành sáu khôi tứ diện bằng nhau.
Giải
Trong hình bên, ta có thể chia thành sáu khối tứ diện bằng nhau như sau:
+ Chia khối lập phương ABCD.A1B1C1D1 thành hai khối lăng trụ tam giác bằng nhau: ABĐ.A1B1D1 và BCD.B1C1D1.
+ Tiếp đồ, lần lượt chia khối lăng trụ ABD.A1B1D1 và BCD.B1C1D1 thành ba tứ diện: DABB1, DAA1B1, DD1A1B1 và DCBB1, DCC1B1, DDiCiBl
+ Ta chứng minh được các khôi tứ diện này bằng nhau như sau:
Hai khối tử diện DABB1 và DAA1B1 bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB1) (1)
Hai khối tứ diện DAA1B1 và DDlAjBi bằng nhau vì chúng đốì
xứng nhau qua mặt phẳng (B1A1D)	(2)
Từ (1) và (2) suy ra ba khối tứ diện DABB1; DAAjBi và DDiAiBj bằng nhau.
- Tương tự, ba khôi tứ diện DCBB1, DCCiB!, DDiCjtBi cũng bằng nhau.
Vậy khối lập phương ABCD.A1B1C1D1 được chia thành sáu khối tứ diện bằng nhau.