Giải bài tập Toán 12 Bài 2: Mặt cầu

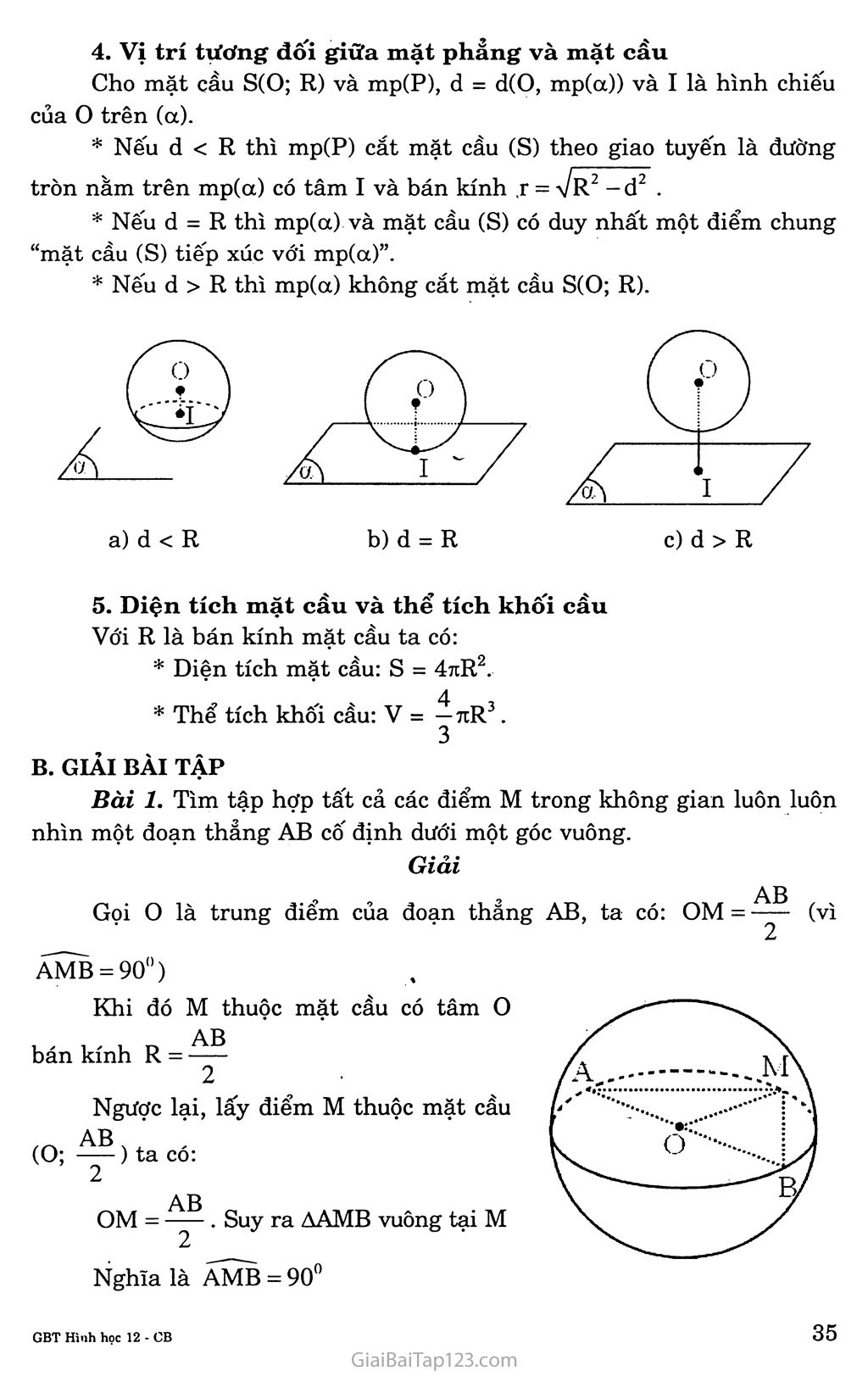
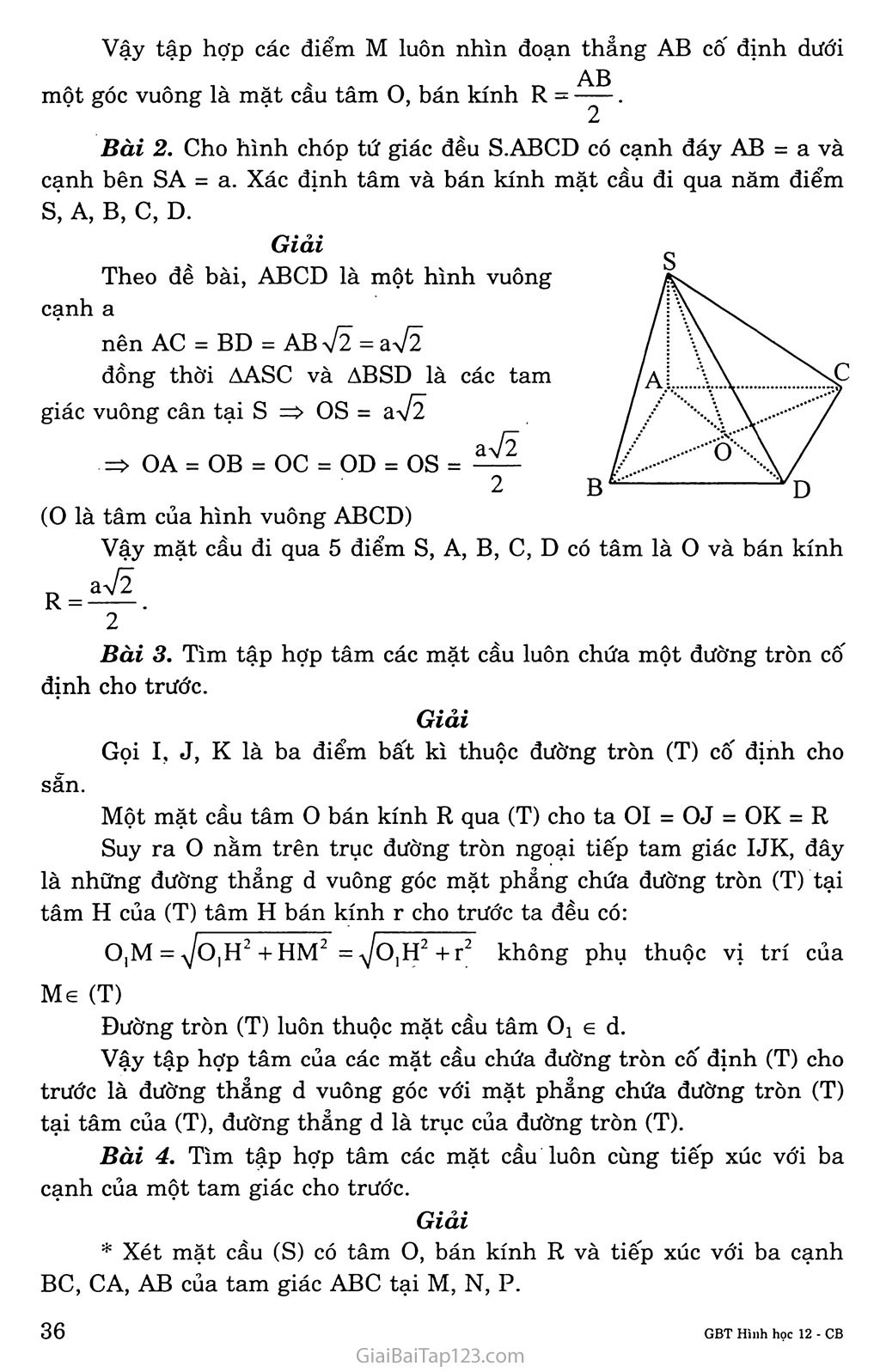
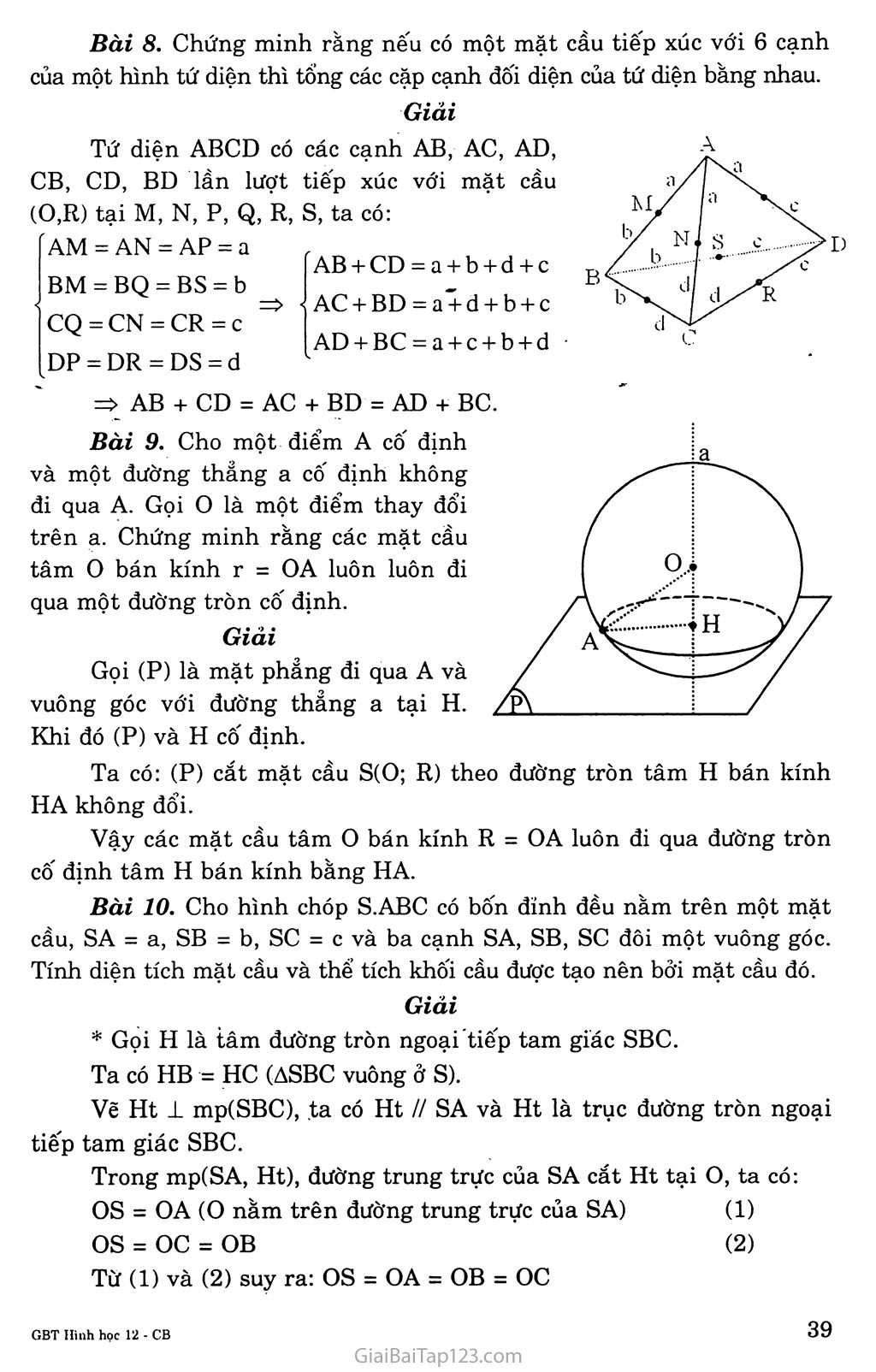
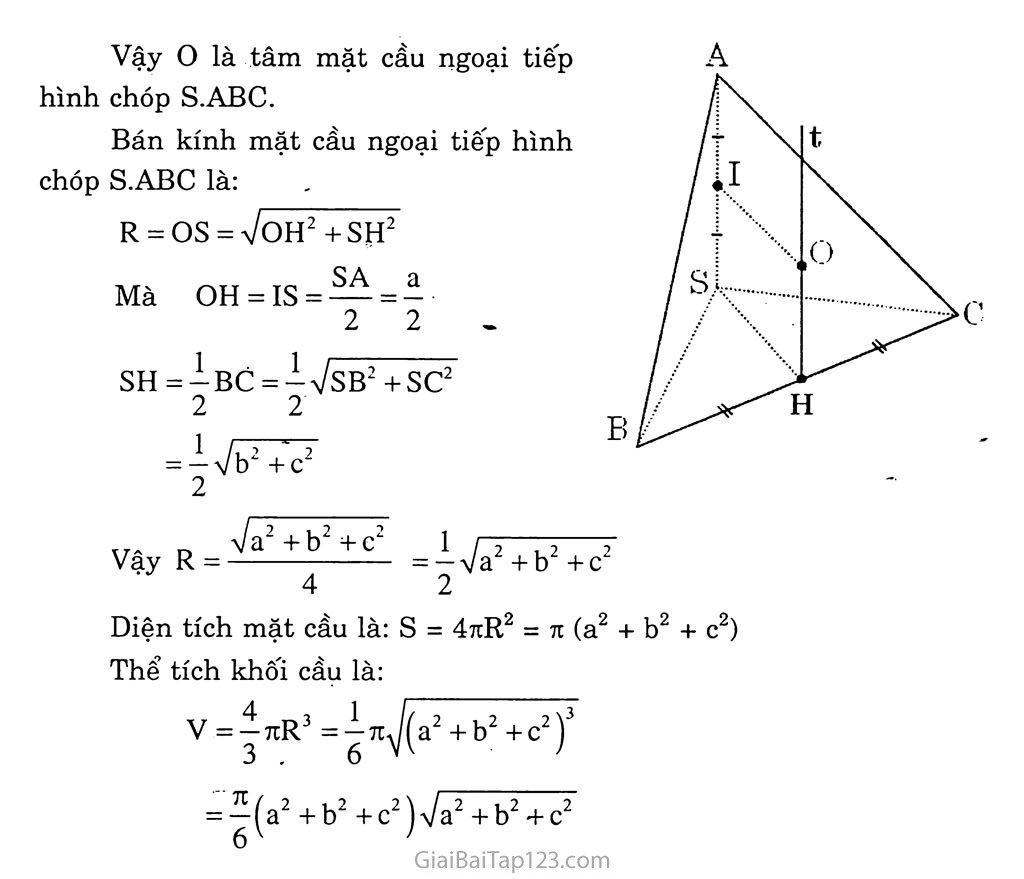
Bài 2. MẶT CẨU
A. KIẾN THỨC CẦN NAM vững
Định nghĩa
Tập hợp các điểm M trong không gian cách điểm o cố định một khoảng R cho trước gọi là mặt cầu tâm 0, bán kính R. Kí hiệu S(0; R).
VỊ trí của một điểm đôi với một mặt cầu
Cho mặt cầu S(0; R) và điểm A.
Nếu OA =	R	thì	A thuộc mặt cầu. OA là bán	kính mặt cầu.
Nếu OA <	R	thì	điểm A nằm trong mặt cầu
Nếu OA >	R	thì	điểm A nằm ngoài mặt cầu.
Khối cầu S(0; R) là tập hợp các điểm M sao cho OM^ R.
Vị trí tương đối giữa đường thẳng và mặt cầu
Cho mặt cầu S(0; R) và đường thẳng A. Gọi I là hình chiếu của o trên A và d = 01.
A
Nếu d = R thì A và mặt cầu (S) có duy nhất một điểm chung Nếu d R thì A không cắt mặt cầu (S).
d = R
Định lí:
Nếu điểm M nằm ngoài mặt cầu (S) thì:
Qua M có vô số tiếp tuyến với mặt cầu (S).
Các đoạn thẳng nối M với các tiếp điểm đều bằng nhau.
Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu (S).
VỊ trí tương đôi giữa mặt phẳng và mặt cầu
Cho mặt cầu S(O; R) và mp(P), d = d(O, mp(a)) và I là hình chiếu của o trên (a).
Nếu d < R thì mp(P) cắt mặt cầu (S) theo giao tuyến là đường tròn nằm trên mp(a) có tâm I và bán kính ,r = \R2 -d2 .
Nếu d = R thì mp(a) và mặt cầu (S) có duy nhất một điểm chung “mặt cầu (S) tiếp xúc với mp(a)”.
Nếu d > R thì mp(a) không cắt mặt cầu S(O; R).
Diện tích mặt cầu và thể tích khôi cầu
Với R là bán kính mặt cầu ta có:
Diện tích mặt cầu: s = 4tiR2.
4
Thể tích khối cầu: V = — 7iR3.
3
B. GIẢI BÀI TẬP
Bài 1. Tìm tập hợp tất cả các điểm M trong không gian luôn luôn nhìn một đoạn thẳng AB cố định dưới một góc vuông.
Giải
„	„ AB
Gọi o là trung điểm của đoạn thẳng AB, ta có: OM = (vì
ẤMB = 90°)
Khi đó M thuộc mặt cầu có tâm o bán kính R =
2
Ngược lại, lấy điểm M thuộc mặt cầu
AB , ’	'
(O; ——) ta có:
2
AB
OM - —- . Suy ra AAMB vuông tại M
Nghĩa là AMB = 90°
Vậy tập hợp các điểm M luôn nhìn đoạn thẳng AB cố định dưới AB
một góc vuông là mặt cầu tâm o, bán kính R =	.
Bài 2. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = a và cạnh bên SA = a. Xác định tâm và bán kính mặt cầu đi qua năm điểm
s, A, B, c, D.
Giải
Theo đề bài, ABCD là một hình vuông cạnh a
nên AC = BD = AB Vĩ = aVz
đồng thời AASC và ABSD là các tam giác vuông cân tại s => OS = aV2
=> OA = OB = oc = OD = OS =
2
(O là tâm của hình vuông ABCD)
Vậy mặt cầu đi qua 5 điểm s, A, B, c, D có tâm là o và bán kính aV2
2
Bài 3. Tìm tập hợp tâm các mặt cầu luôn chứa một đường tròn cố định cho trước.
Giải
Gọi I, J, K là ba điểm bất kì thuộc đường tròn (T) cố định cho sẵn.
Một mặt cầu tâm o bán kính R qua (T) cho ta OI = OJ = OK = R
Suy ra 0 nằm trên trục đường tròn ngoại tiếp tam giác IJK, đây là những đường thẳng d vuông góc mặt phảng chứa đường tròn (T) tại tâm H của (T) tâm H bán kính r cho trước ta đều có:
O,M = ^OjH2 + HM2 = ạ/o,H2 +r2 không phụ thuộc vị trí của
Me (T)
Đường tròn (T) luôn thuộc mặt cầu tâm Ũ! e d.
Vậy tập hợp tâm của các mặt cầu chứa đường tròn cố định (T) cho trước là đường thẳng d vuông góc với mặt phẳng chứa đường tròn (T) tại tâm của (T), đường thẳng d là trục của đường tròn (T).
Bài 4. Tìm tập hợp tâm các mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.
Giải
* Xét mặt cầu (S) có tâm o, bán kính R và tiếp xúc với ba cạnh BC, CA, AB của tam giác ABC tại M, N, p.
H là hình chiếu vuông góc của o trên mp(ABC), ta có: OM ± AB => BM ± AB (theo định lí ba đường vuông góc) Tương tự: HN 1 BC, HP 1 AC
Ta có: OM = ON = OP = R
Khi đó AOHM = AOHN = AOHP
Suy ra HM = HN = HP
Chứng tỏ H là tâm đường tròn nội tiếp tam giác ABC.
Vậy tâm o của mặt cầu thuộc đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm H của đường tròn nội tiếp tam giác ABC.
* Lấy điểm o thuộc trục đường tròn nội tiếp tam giác ABC.
Đường tròn nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại N, p, M, ta có: HM ± AB, HN 1 BC, HP 1 CA
=> OM 1 AB, ON 1 BC, OP 1 CA	(1)
Mặc khác: HM = HN = HP => AOHM = AOHN= AOHP
=> OM = ON = OP	(2)
Từ (1) và (2) suy ra mặt cầu (S) tiếp xúc với ba cạnh của tam giác ABC.
Vậy tập hợp tâm của các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là trục của đường tròn nội tiếp tam giác ABC.
Bài 5. Từ một điểm M nằm ngoài mặt cầu (O; R), vẽ hai đường thẳng cắt mặt cầu lần lượt tại A, B và c, D.
Chứng minh rằng MA.MB = MC.MD
Gọi MO = d. Tính MA.MB theo R và d.
Giải
a) Vì AB và CD cắt nhau nên chúng cùng nằm trong một mặt
phảng.
Mặt phẳng chứa AB và CD cắt mặt cầu (O;R) theo đường tròn đi qua bốn điểm A, B, c, D.
Trong mặt phẳng đó ta có:
MÃ.MB = (mĨ + ĨÃ)(mỉ + Ĩb) (I là trung điểm của AB)
= (mĩ+ĩã)(mĩ-ĩấ) vì ĨỖ = -ĨÃ
■ = MĨ2-ĨÃ2 = (mo2-oi2)-ia2
= MO2-(OI2+IA2) = MO2-OA2 =MO2-R2 (1)
Tương tự, ta có MC.MB = MO2 -R2	(2)
Từ (1) và (2) suy ra MA.MB = MC.MD
Vậy MA.MB = MC.MD.
Ta có: MA.MB = OM2-R2 = d2-R2	(3)
Vì MA và MB cùng hướng nên MA.MB = MA.MB (4)
Từ (3) và (4) suy ra MA.MB = d2 -R2.
Bài 6. Cho mặt cầu (O;R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phai là điểm đối xứng với I qua tâm o. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng AMB = AIB.
Giải
Mặt cầu S(O; R) tiếp xúc với mp(P) tại I và IA c mp(P)
=> AI là tiếp tuyến tại I của mặt cầu (O)
=> AM và AI là hai tiếp tuyến của mặt cầu (S)
Khi đó AM = AI
AC
Tương tự, BM = BI suy ra AAMB = AAIB Vậy AMB = ẤĨB.
Bài 7. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA’ = a, AB = b, AD = c.
Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.
a) Gọi o là tâm của hình hộp chữ nhật, ta có:
OA = OB = oc = OD = OA’ = OB’ = OC’ = OD’ =
2
Giải
Vì AC’ =
+ b2 +c2
+ b2 +c2 nên OA = ... = OD’= Ạ
2
Vậy mặt cầu đi qua tám đỉnh của hình hộp chữ nhật
ABCD.A’B’C’D’ có tâm là o và bán kính R = 	y	
2
b) Mặt cầu (O; R) cắt mp(ABCD) theo giao tuyến là đường tròn (C) ngoại tiếp hình chữ nhật ABCD, bán kính của đường tròn (C) là:
AC r = —
2
= ^-Vb2 + c2
2
Bài 8. Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng các cặp cạnh đối diện của tứ diện bằng nhau.
Giải
Tứ diện ABCD có các cạnh AB, AC, AD, CB, CD, BD lần lượt tiếp xúc với mặt cầu (O,R) tại M, N, p, Q, R, s, ta có:
AM = AN = AP = a
BM = BQ = BS = b ' CQ = CN = CR = c
AB + CD — a + b + d + c
AC + BD = a + d + b + c
AD + BC = a + c + b + d
DP = DR = DS = d
=> AB + CD = AC + BD = AD + BC.
Bài 9. Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi o là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm 0 bán kính r = OA luôn luôn đi qua một đường tròn cố định.
Giải
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H bán kính HA không đổi.
Vậy các mặt cầu tâm o bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.
Bài 10. Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, sc = c và ba cạnh SA, SB, sc đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Giải
* Gọi H là tâm đường tròn ngoại tiếp tam giác SBC.
Ta có HB = HC (ASBC vuông ở S).
Vẽ Ht 1 mp(SBC), .ta có Ht // SA và Ht là trục đường tròn ngoại tiếp tam giác SBC.
Trong mp(SA, Ht), đường trung trực của SA cắt Ht tại o, ta có:
OS = OA (O nằm trên đường trung trực của SA) (1)
OS = oc = OB	(2)
Từ (1) và (2) suy ra: OS = OA = OB = oc
Vậy o là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
R = OS = Voh2+sh2
Mà OH = IS = -^ = Ặ
2	2
SH = ẬbÓ = ịựsB2 +SC2
2	2
= ^7b2 + c2
2
2+c2
_ Va2+b2+e2 _ 1 [J—
Vậy R =	—	 = -t Va +