Giải bài tập Toán 12 ÔN TẬP CUỐI NĂM

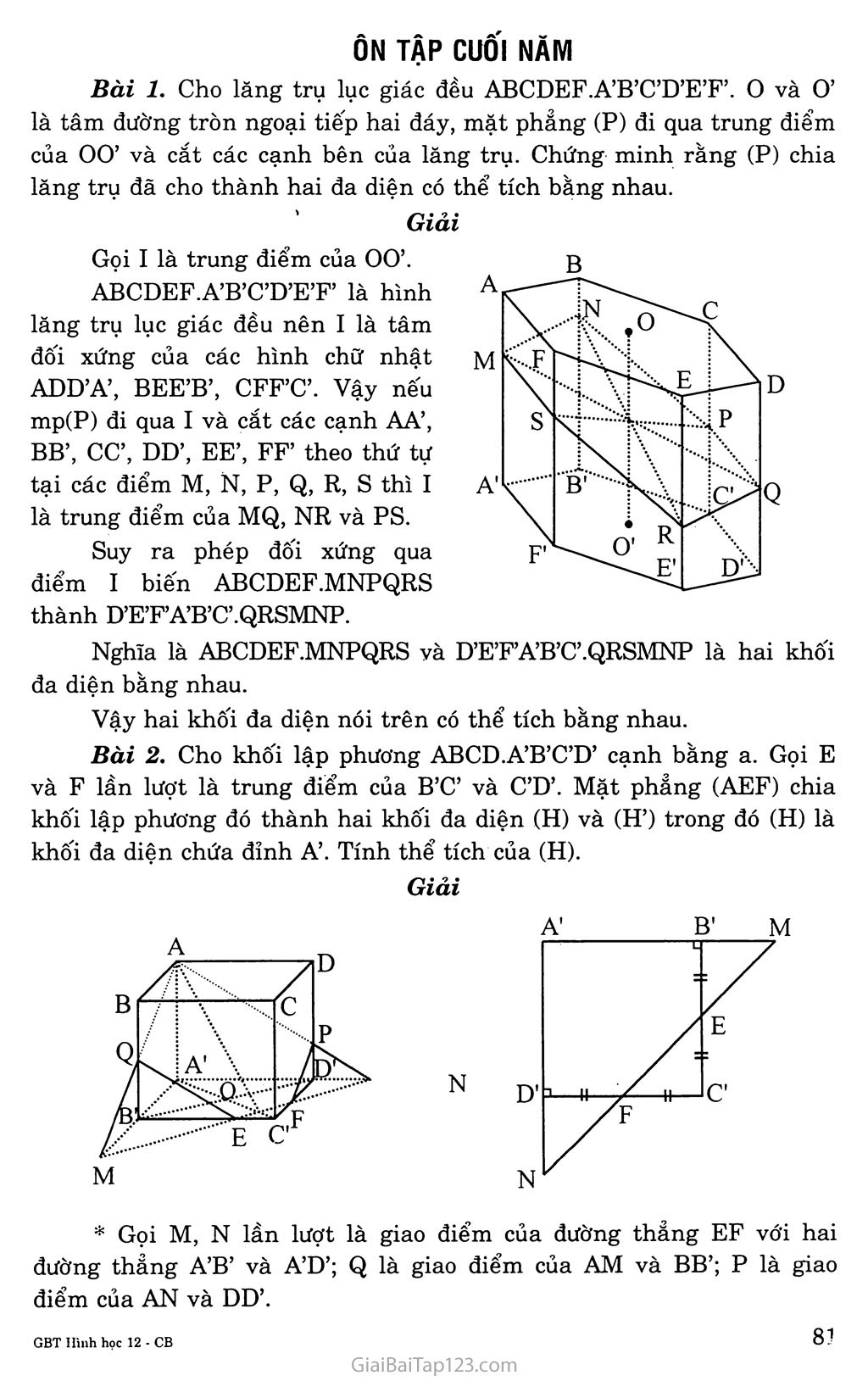
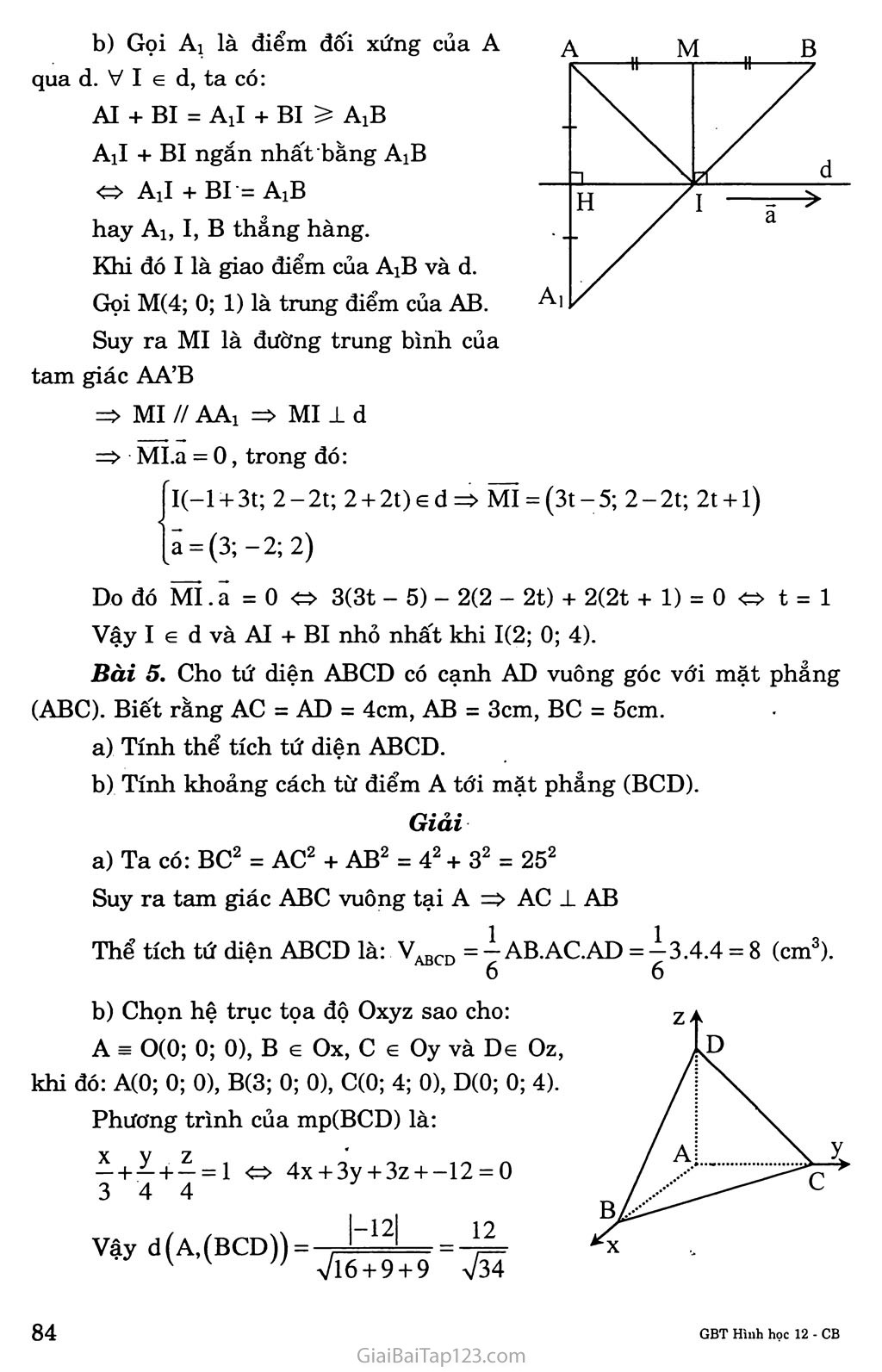
ÔN TẬP cuôì NĂM
Bài 1. Cho lăng trụ lục giác đều ABCDEF.A’B’C’D’E’F’. o và 0’ là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của 00’ và cắt các cạnh bên của làng trụ. Chứng minh rằng (P) chia lăng trụ đã cho thành hai đa diện có thể tích bằng nhau.
Giải
Gọi I là trung điểm của 00’.
ABCDEF.A’B’C’D’E’F’ là hình lăng trụ lục giác đều nên I là tâm đối xứng của các hình chữ nhật ADD’A’, BEE’B’, CFF’C’. Vậy neu mp(P) đi qua I và cắt các cạnh AA’, BB’, CC’, DD’, EE’, FF’ theo thứ tự tại các điểm M, N, p, Q, R, s thì I là trung điểm của MQ, NR và PS.
Suy ra phép đối xứng qua điểm I biến ABCDEF.MNPQRS thành D’E’F’A’B’C’.QRSMNP.
B
Nghĩa là ABCDEF.MNPQRS và D’E’FA’B’C’.QRSMNP là hai khối đa diện bằng nhau.
Vậy hai khối đa diện nói trên có thể tích bằng nhau.
Bài 2. Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Gọi E và F lần lượt là trung điểm của B’C’ và C’D’. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H’) trong đó (H) là khối đa diện chứa đỉnh A’. Tính thể tích của (H).
M
Giải
* Gọi M, N lần lượt là giao điểm của đường thẳng EF với hai đường thẳng A’B’ và A’D’; Q là giao điểm của AM và BB’; p là giao điểm của AN và DD’.
Ta có mp(AEF) cắt hình lập phương ABCD.A’B’C’D’ theo thiêt diện là ngũ giác AQEFP.
* Tam giác D’FN vuông cân ở D’ và D’F = -y
A 'AT 3a
nên ta có D N = — => A N = -7-
ABCD.A'B'C'D' a
Gọi ■
ABCD.QECFP’ v2
AQEFP.B'A'D’
A.MA'N
V. = v_	Va
v4 v PFD'N ’ v5
QMB'E
Ta có V4 = v5
V, =-AA'.A'M.A'N = -.a.^.^ 3a
■	2 2
v4 = |pD'.D'F.D’N = 1 a
6
a a a3
2 2 72
V2 = V3 - (V4 + V,) = V, - 2 V4 =	- A- =
25a3
72
Vậy mp(AEF) chia khối lập phương ABCD.A’B’C’D’ thành hai khôi đa diện và thể tích của khối đa diện chứa đỉnh A’ là:
V, = v.„„	
v2 v AQEFP.B'A'D'
25a3
72
Bài 3. Cho mặt cầu (S) tâm o bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó.
Thể tích của khối nón theo r và h.
Xác định h để thể tích của hình nón là lớn nhất.
Giải
Gọi H là tâm mặt đáy của hình nón, o là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.
Khi đó IK là đường kính của mặt cầu (S) và IK = 2r.
Gọi M là một điểm thuộc (C).
Tam giác IMK vuông ở M và có đường cao MH nên:
MH2 = IH.HK = h(2r - h).
Thể tích khôi nón là:
V = 17C.MH2 .IH = I ,h (2r - h) .h = h2 (2r - h)
V đạt giá trị lớn nhất khi hàm số f(h) = h2(2r - h) = -h3 + 2rh2 đạt giá trị lớn nhất.
f(h) = -3h2 + 4rh = h(-3h + 4r), 0 < h < 2r
/1 T»
f(h) = 0 h = 0 Ể (ũ; 2r), h = y e (0; 2r)
lì
0
41-
2r
f'(h)
0
+
0
-
f'(h)
4r
Vậy V đạt giá trị lớn nhất khi h = -y
Bàì 4. Trong không gian Oxyz cho hai điểm A(l; 2; -1), B(7; -2; 3) fx = -l + 3t
và đường thẳng d có phương trình < y = 2 - 2t .
z = 2 + 2t
Chứng minh rằng hai đường thẳng d và AB cùng nằm trong một mặt phẳng.
Tìm điểm I trên d sao cho AI + BI nhỏ nhất.
Giải
Đường thẳng d có vectơ chỉ phương là a = (3; -1; 2).
Ta có: ÃB = (6; -4; 4)
Ta thấy AB = 2a và A e đường thẳng AB nhưng A Ể d => AD // d.
Vậy hai đường thẳng AB và d cùng nằm trong một mặt phẳng.
Gọi Aị là điểm đốì xứng của A qua d. V I e d, ta có:
AI + BI = Ail + BI A1B
All + BI ngắn nhất'bằng A1B
« All + BI = A1B hay Al, I, B thẳng hàng.
Khi đó I là giao điểm của A1B và d. Gọi M(4; 0; 1) là trung điểm của AB. Suy ra MI là đường trung bình của tam giác AA’B
=> MI // AA1 => MI ± d
=> MLa = 0, trong đó:
ì(-l + 3t; 2-2t; 2 + 2t)ed=> MI = (3t-5; 2-2t; 2t + 1) ã = (3;-2; 2)
Do đó MI .ã =0 o 3(3t - 5) - 2(2 - 2t) + 2(2t + l) = ot=l Vậy I e d và AI + BI nhỏ nhất khi 1(2; 0; 4).
Bài 5. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC). Biết rằng AC = AD = 4cm, AB = 3cm, BC = 5cm.
Tính thể tích tứ diện ABCD.
Tính khoảng cách từ điểm A tới mặt phẳng (BCD).
Giải
Ta có: BC2 = AC2 + AB2 = 42 + 32 = 252
Suy ra tam giác ABC vuông tại A => AC ± AB
Thể tích tứ diện ABCD là: V^CD = y AB.AC.AD = y 3.4.4 = 8 (cm3). 6	6
Chọn hệ trục tọa độ Oxyz sao cho:
A = 0(0; 0; 0), B e Ox, c e Oy và De Oz, khi đó: A(0; 0; 0), B(3; 0; 0), C(0; 4; 0), D(0; 0; 4).
Phương trình của mp(BCD) là: 4+4+4-1 4x + 3y + 3z + -12 = 0
4 4
Vậy d(A,(BCD)) = -	=-^=
v k ” V16 + 9 + 9 V34
Bài 6. Trong không gian Oxyz, cho mặt cầu (S) có phương trình: X2 + y2 + z2 = 4a2 (a > 0).
Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.
Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Xác định tâm và bán kính của (C).
Tính diện tích xung quanh của hình trụ nhận (C) làm đáy và có chiều cao bằng ã-\Í3 . Tính thể tích của khôi trụ tương ứng.
Giải
a) Ta có: 0(0; 0; 0) là tâm mặt cầu (S), bán kính của (S) là 2a.
Diện tích của mặt cầu (S) là: Sc = 4x R2 = 16x a2
4	3	32	3
Thể tích của khôi cầu là: Vr = — 7iR3 = ^-—7ta3
c 3	3
Mp(Oxy) đi qua tâm o của mặt cầu (S) nên mp(Oxy) cắt (S) theo đường tròn lớn (C)
Khi đó (C) có tâm 0(0; 0; 0) và bán kính r = R - 2a
Diện tích xung quanh của hình trụ là:
SXq = 2x rh = 2x.2a.aV3 = 4x a2 V3
Thể tích của khối trụ là: V = lĩ r2h = 4x a3 y/3
Bài 7. Trong không gian Oxyz cho hai đường thẳng:
x = l-t
y = t
z = -t
d2:<
x = 2t'
y = -l + t'
z = t'
Chứng minh rằng hai đường thẳng di và d2 chéo nhau.
Viết phương trình mp(a) chứa di và song song với d2
Giải
Ta có: Vectơ chỉ phương của đường thẳng di là a, = (-1; 1; -1) Vectơ chỉ phương của đường thẳng d2 là a2 = (2; 1; 1)
Ta có:	ai và ãĩ không cùng phương	(1)
Hệ phương trình di và d2 vô nghiệm	(2)
Từ (1) và (2) suy ra di và d2 là hai đường thẳng chéo nhau.
Mặt phẳng(a) đi qua điểm Mj (1; 0; o) e dị và có vectơ pháp tuyến n vuông góc với hai vectơ a, và a, , n = I A a21 = (2; -1; 3)
Khi đó phương trình của mp(a) là: 2(x — 1) - y - 3z = 0 2x-y-3z — 2 = 0
Bài 8. Trong không gian Oxyz cho các điểm A(l; 0; -1), B(3; 4; -2), C(4; -1; 1), D(3; 0; 3).
Chứng minh rằng A, B, c, D không đồng phẳng.
Viết phương trình mặt phẳng (ABC) và tính khoảng cách từ D đến (ABC).
Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD.
Tính thể tích tứ diện ABCD.
Giải
a) Mp(ABC) có vectơ chỉ phương n vuông góc với hai vectơ AB = (2;4;-1) và Ãc = (3;-1; 2), n = [ÃBaÃc) = (7;-7;-14)
Phượng trình của mp(ABC) là:
7(x - 1) - 7(y - 0) - 14(z + 1) = 0 X — y — 2z — 3 = 0 XD - yD - 2zd -3 = 3-0- 2(3) -3^0
Suy ra D Ể mp(ABC)
Vậy Bôn điểm A, B, c, D không đồng phẳng.
, ' x	|3-0-2(3)-3|	6. rr
b) Ta có: d(D, mp(ABC)) = J	; v 7 1 = ~ = Vó
v 77 Vl + 1 + 4 Vó
Ta có:
Ãẽ = (2;4;-1), ÃD = (2;0;4), CB = (-l;5;-3), CD = (-1;1;2)
=>ÃB.ÃD = 0 và CB.CD = 0
=>ABJ_AĐ và CB1CD
Nghĩa là hai tam giác ABD và CBD lần lượt vuông ở A và c.
=> MA = MC =	= MB = MD (M ià trung điểm của cạnh BD).
Vậy mặt cầu ngoại tiếp tứ diện ABCD có tâm MI 3; 2; 4 I và bán l 2;
lz v „ BD VO + 16 + 25 Vĩĩ
kính R = — =	—	 ——
2	2	2
Phương trình mặt cầu ngoại tiếp tứ diện ABCD là: ox2 . /.. nx2 .	1?	41
(x-3)2+(y~2) +ự--|j = y
Ta có: VABCD = |.SAABC.DH
Mặc khác: ÃB = (2; 4; -1) và Ãc = (3; -1; 2)
=> AB.AC = 0 => AB ± AC . Nghĩa là tam giác ABC vuông ở A.
Khi đó SAABC =|.AB.AC = |.V2Ĩ.VĨ4 =-|ự6
và DH = d(D, mp(ABC)) = Vó
Vậy Vabcd = “••“■Vố.x/ó = 7 (đơn vị thể tích).
Bài 9. Trong không gian Oxyz cho bốn điểm A(2; 4; -1), B(l; 4; —1), C(2; 4; 3), D(2; 2; -1)
Chứng minh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một. Tính thể tích khôi tứ diện ABCD.
Viết phương trình mặt cầu (S) đi qua bôn điểm A, B, c, D
Viết phương trình mặt phẳng (a) tiếp xúc với mặt cầu (S) và song song với mp(ABD).
Giải
a) * Ta có: ÃB = (-1;O;O),
ÃC = (0;0;4), ÃD = (0;-2;0)
=> ÃB.ÃC = ÃC.ÃD = ÃĐ.ÃB = 0 =>AB±AC, AC1AD, AD1AB.
Thể tích khối tứ diện ABCD là:
VABCD =yAB.AC.AD = Ỵ (đơn vị thể tích).b) Phương trình mặt cầu (S) ngoại tiếp ABCD có dạng: X2 + y2 + z2 + 2ax + 2by + 2cz + d = 0 (*)
Lần lượt thay tọa độ của A, B, c, D vào (*) ta được:
4a + 8b-2c + d =-21 (1) 2a + 8b-2c + d =-18 (2) 4a+ 8b + 6c + d =-20 (3) 4a + 4b-2c + d = -9 (4)
+ 16 + 1 +4a + 8b-2c + d = 0
1 +16 +1 + 2a + 8b — 2c + d =0
4 + 16 + l + 2a + 8b + 6c + d = 0
4 + 4 + 1 +4a + 4b-2c + d =0
	 3
Từ (1) và (2) suy ra a = -4-
	 31
Từ (2) và (4) suy ra 2a - 4b = 9 => 2	- 4b = 9 => b = _ 3
V 2;
Từ (3) và (4) suy ra 4b +8c = -20 => 4(-3) + 8c = -2Ó => c = -1
Thay kết quả a, b, c vào (1) ta được:
4Í-|j + 8(-3)-2(-l) + d = -21d=7
Vậy mặt cầu (S) có phương trình là:
X2 + y2 + z2 - 3x - 6y - 2z + 7 = 0 (	3 Ỵ /	/	'2 21
« ^x-jj + (y-3) +(z-l) =^-
Mặt phẳng (a) song song với mp(ABD) nên vectơ chỉ phương của mp(a) vuông góc với hai vectơ AB = (-1; 0; o) và AD = (0; —2; o).
Ta có n = (aB a ad) = (0; 0; 2) hay n = (0; 0; 1).
Khi đó phương trình của mp(a) có dạng z + D = 0 Mp(a) tiếp xúc với mặt cầu (S) nên:
Vậy có hai mặt phẳng (a): z -1 +
V2Ĩ
2
= 0 và z — 1 —
V2Ĩ
X = 1 - 2t
Bài 10. Trong không gian Oxyz cho đường thẳng d:
z = 3-t
và mặt phẳng (a): 2x + y + z - 0.
Tìm tọa độ giao điểm A của d và (cc).
Viết phương trình mặt phẳng (p ) qua A và vuông góc với d.
Giải
Phương trình tham số’ của đường thẳng d là a = (-2; 1; — 1).
mì .	,	,	z	7
Thay vào phương trình mp(ct) ta tính được t = — 4
Vậy giao điểm của đường thẳng d và mp(a) là a[ - —; -ỉ-^; — I < 4 4 4;
Vì Mp(0) vuông góc với đường thẳng d nên mp(P) có vectơ pháp tuyến n cùng phương với vectơ chỉ phương a của đường thẳng d. Khi đó lĩ = ã = (-2; 1; -1).
15
J , 10 ì , iL 15 ì J ■ 5 La
I 4 J I 4 J Ả 4/
Vậy phương trình của mp( p ) là: J 10^ .í
l 4 ) l'
30
 -2x + y - z - — = 0 4x - 2y + 2z +15 = 0
4
Bài 11. Trong không gian Oxyz cho các điểm A(-l; 2; 0), B(-3; 0; 2), C(l; 2; 3), D(0; 3; -2).
Viết phương trình mặt phẳng (ABC) và phương trình tham số' của đường thẳng AD.
Viết phương trình mặt phẳng (a) chứa AD và song song với BC.
Giải
a) Vì mp(ABC) có vectơ pháp tuyến n vuông góc vói hai vectơ ÃB = (-2;-2;2) và ÃC = (2;0;3) nên n = (ÃBaÃc) = (-6;10;4)
Khi đó phương trình của mp(ABC) là:
-6(x + 1) + 10(y - 2) - 4(z - 0) = 0 « 3x - 5y - 2z + 13 = 0
Đường thẳng AD đi qua điểm A nên có vectơ chỉ phương là ĂD = (1; 1; -2)
Vậy phương trình tham số của đường thẳng AD là <
x = -l + t y = 2 +1
z = -2t
b) Mp(a) chứa AD và song song với BC nên có vectơ pháp tuyến n vuông góc với hai vectơ AD = (1; 1; -2) và BC = (4; 2; 1) .
Khi đó n = (ÃDAẼc) = (5;-9;-2).
Vậy phương trình của mp(a) là:
5(x + 1) - 9(y - 2) - 2(z - 0) = ọ 5x - 9y - 2z + 23 = 0
Bài 12. Trong không gian Oxyz cho bốn điểm A(3; -2; -2), B(3; 2; 0), C(0; 2; 1) và D(-l; 1; 2)
Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (BCD).
Tìm tọa độ tiếp điểm của (S) và mặt phẳng (BCD).
Giải
a) Mp(BCD) có vectơ pháp tuyêh n vuông góc với hai vectơ BC = (-3;0; 1) và BD = (-4; -1; 2), n = (ẼCABD) = (l; 2; 3)
Phương trình của mp(BCD) là: l(x - 3) + 2(y - 2) + 3(z - 0) = 0
(1)
 x + 2y + 3z-7 = 0
Thay tọa độ của A vào (1) ta có:
XA + 2yA + 3zA - 7 = (3) + 2(-2) + 3(-2) - 7 = -14 * 0
Suy ra A Ễ (BCD)
Vậy ABCD là một tứ diện.
b) Mặt cầu (S) có tâm A và tiếp xúc với mp(BCD) nên có bán kính:
R = d(A, (BCD)) = VĨ4
Gọi H là tiếp điểm của (S) và mp(BCD), IH ± (BCD)
Khi đó phương trình tham số của đường thẳng IH là:
X = 3 + t y = -2 + 2t z = -2 + 3t
Thay X, y, z trong phương trình tham số của đường thẳng IH vào phương trình của mp(a), ta có t = 1.
Vậy tiếp điểm của (S) và mp(BCD) là H(4; 0; 1).
Bài 13. Trong không gian Oxyz cho hai đường thẳng:
d,:
X =-1 + 3t
y = l + 2t
và d2:
z = 3-2t
X = t
< y = l + t
z = -3 + 2t
Chứng minh di và d2 cùng thuộc một mặt phẳng.
Viết phương trình mặt phẳng đó.
.	Giải
-l + 3t = t'
a) Giải hệ phương trình:
■ 1 + 2t = 1 +1' ta được ■
3-2t = -3 + 2t'
Nghĩa là hai đường thẳng di và d2 cắt nhau tại A(2; 1; 3).
Vậy hai đường thẳng di và d2 cùng thuộc mặt phẳng.
b) Mặt phẳng (Q) đĩ qua điểm A(2; 3; 1) và có vectơ pháp tuyến vuông góc với hai vectơ a, và a2, n = ( a, A a2) = (6; - 8; 1).
Vậy phương trình' của mặt phẳng (Q) chứa di và d2 là:
6(x - 2) - 8(y - 3) + (z - 1) = 0 6x - 8y + z + 11 = 0.
Bài 14. Trong không gian cho ba điểm A, B, c.
Xác định điểm G sao cho: GA + 2GB - 2GC = õ
Tìm tập hợp các điểm M sao cho: MA2 +2MB2 -2MC2 = k2, với K là hằng số.
Giải
Ta có: GÃ + 2GB - 2GC = õ
« GÃ + 2(ÕẤ + Ãb)-2(ÕÃ + Ãc) = õ
 GÃ + 2(ÃB - Ãc) = õ AG = 2(ÃB - Ãẽ)
Vậy AG = 2CB. Đây chính là hệ thức để xác định vị trí điểm G khi biết vị trí ba điểm A, B, c.
Ta có MA2 + 2MB2 - 2MC2 = k2
«(gÃ-Õm)2 +2(gB-Gm)2-2(gC-Gm)2 = k2
« (ga2 + 2GB2 - 2GC2)-2GM (ga + 2GB - 2GC) + GM2 = k2
õ
« GM2 = k2 - (ga2 + 2GB2 - 2GC2)
Vì G cố định nên GA2 +2GB2 -2GC2 không đổi.
Vậy GM2 không đổi.
Nếu k2 < GA2 +2GB2 -2GC2 thì tập hợp M là tập rỗng (0).
Nếu k2 = GA2 + 2GB2 -2GC2 thì M = G
Nếu k2 > GA2 +2GB2 -2GC2 thì tập hợp của M là mặt cầu tâm G,
bán kính R =
k2 -(ga2 +2GB2 -2GC2).
Bài 15. Cho hai đường thẳng chéo nhau:
X = 2 + 2t
X = 2-t
dJ
y = -1 + t và d’: <
z = l-t
Viết phương trình các mặt phẳng (a) va (p) song song với nhau và lần lượt chứa d và d’.
Lấy hai điểm M(2; -1; 1) và M’(2; 0; 1) lần lượt trên d và d’. Tính khoảng cách từ M đến'mặt phẳng (P) và khoảng cách từ M’ đến mặt phẳng (a). So sánh hai khoảng cách đó.
Giải
a) Vectơ chỉ phương của hai đường thẳng d và d’ lần lượt là: ũ = (-1; 1; -1) và V = (2; 1; 1).
Ta có: M(2; -1; 1) G d và M’(2; 0; 1) e d’.
Vì mp(a) chứa d và song song với d’, mp( p) chứa d’ và song song với d nên (cc) // (P). Hai mặt phảng có cùng vectơ chỉ phương n vuông góc với hai vectơ u và V . Vậy n = u A V = (2;-l;-3)
Phương trình của mp(a) là:
2(x - 2) -l(y + 1) - 3(z - 1) = 0
2x - y — 3z - 2 = 0
Phương trình của mp( p )là:
2(x - 2) - Ky - 0) - 3(z - 1) = 0
 2x — y — 3z—1 = 0
b) Ta có: d(M,mp(P)) = L^-/====—- = -X=
v v 77	V4+1+9 Vũ
,	/XX l2(2)-°"3(1)l 1
và d(M',mp(q)) = V7 =M = -d=
1
v	v 77	V4+1+9	Vũ
Vậy d(M',mp(a)) = d(M,mp(P)) =
Bài 16. Trong không gian Oxyz cho mặt phẳng (a) có phương trình 4x + y + 2z + 1 - 0 và mặt phẳng (p) có phương trình 2x - 2y + z + 3 = 0.
■ a) Chứng minh rằng (a) cắt (p )
Viết phương trình tham số của đường thẳng d là giao của (a) và (p )
Tìm điểm M’ là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (cc).
Tìm điếm N’ là ảnh của N(0; 2; 4) quá phép đô'i xứng qua đường thẳng d.
Giải
Hai đường thẳng (a) và (p) có vectơ pháp tuyến của lần lượt là:
n, =(4; 1; 2) và n2 = (2; -2; 1)
Suy ra n, và n2 không cùng phương.
Vậy hai mặt phẳng (a) và (p ) cắt nhau.
Gọi d là giao tuyến của hai mặt phẳng (a) và (P )
Suy ra d có vectơ pháp tuyến u vuông góc với hai vectơ và n2
Khi đó: U = [n/An^ = (5; 0; -io) = (l; 0; -2)
Vậy.fu0=|uì
Ta có: A(0; 1; -1) e (a) n (P )
=> A(0; 1; -1) e d
x = t
Phương trình tham sô' của d là: ■
y = l
z -—1 — 2t
Gọi M’ là ảnh của M(4; 2; 1) qua phép đôì xứng qua mp(a)
'x = 4 + 4t
Phương trình tham số của đường thẳng MM’ là:
z = l + 2t
Thay X, y, z trong phương trình tham số của đường thẳng MM’ vào phương trình mp(a), ta có:
4(4 + 4t) + (2 + t) + 2(1 + 2t) + 1 = 0 t = -1
Giao điểm của đường thẳng MM’ và mp(a) là H(0; 1; -1).
M’ và M đối xứng với nhau qua mp(a) nên H là trung điểm của MM’.
xm.=2xh-xm=-4
' yM'=2yH-yM =0
zM=2zH-zM = -3
Vậy M’(-4; 0; -3)
Đường thẳng d có vectơ chỉ phương u = (1; 0; -2)
Điểm K(t; 1; -1 - 2t) e d
Ta có NK = (t;-l;-2t-5)
K là hình chiếu vuông góc của N trên đường thẳng d.
aNK 1 d o NK.U = 0
 t + 0 + 4t + 10 = 0 t =-2
Vậy K(-2; 1; 3)
N’ đối xứng với N qua đường thẳng d nên K là trung điểm của NN’ X = 2xK -XN = -4
Vậy N’ có tọa độ ■
y = 2yK-yN=0 => N’(-4; 0; 2).
z = 2xk-zn =2