Giải bài tập Toán 12 Bài 3. Khái niệm về thể tích của khối đa diện

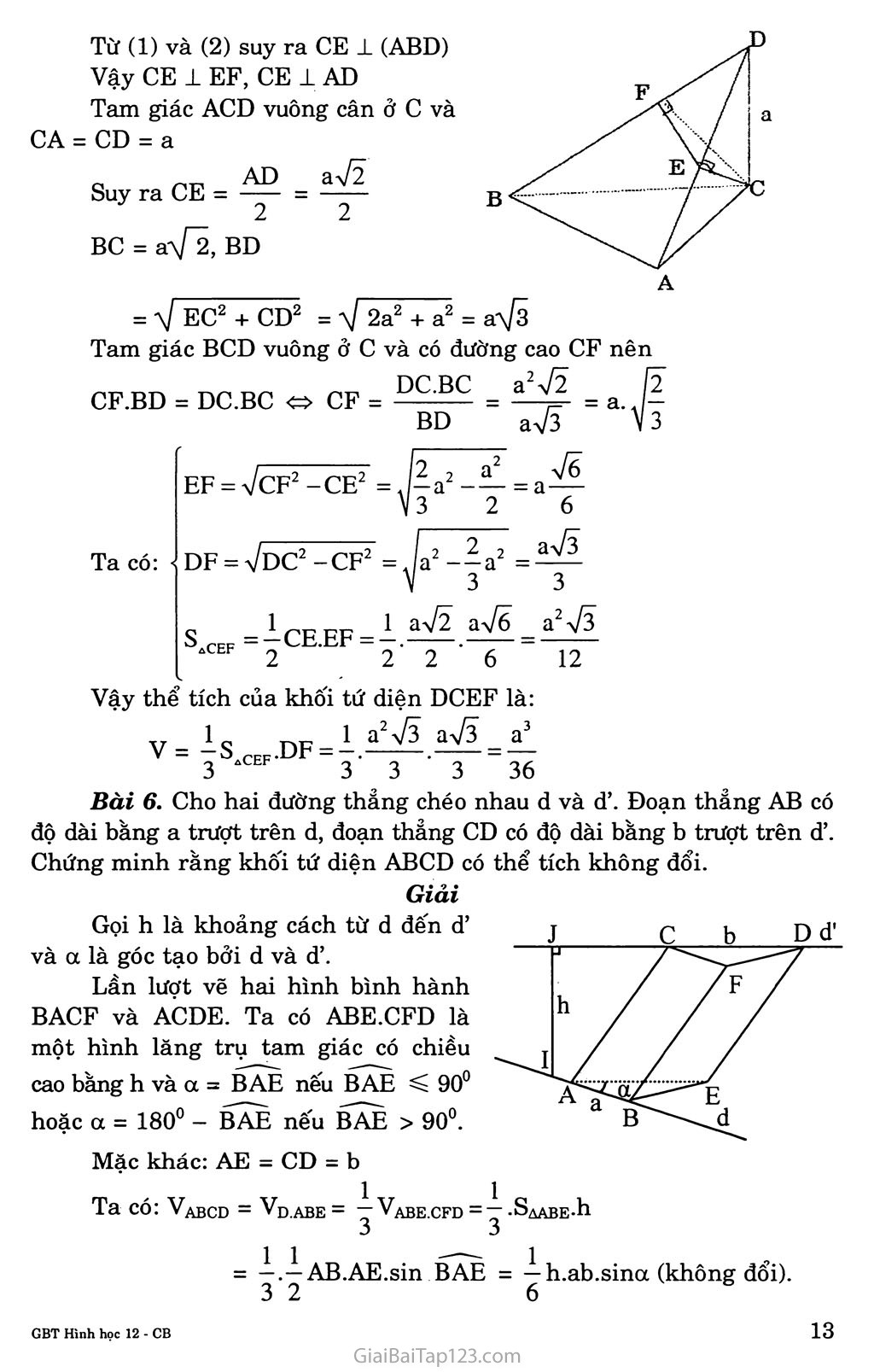
Bài 3. KHÁI NIỆM VỀ THỂ TÍCH CỦA KHÔÌ ĐA DIỆN
A. KIẾN THỨC CẦN NAM vững
Hai khối đa diện bằng nhau thì có thể tích bằng nhau.
Nếu một khối đa diện được phân chia thành nhiều khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ đó.
Khôi lập phương có cạnh bằng 1 thì có thể tích bằng 1.
* Công thức tính thể tích các khối đa diện:
Khối lăng trụ: V = s.h trong đó s là diện tích đáy, h là chiều cao.
Khối chóp: V = ^- s.h trong đó s là diện tích đáy, h là chiều cao.
Khối hộp chữ nhật: V = abc trong đó a, b, c là ba kích thước.
Khối lập phương: V = a3 trong đó a là độ dài cạnh.
B. GIẢI BÀI TẬP
Bài 1. Tính thể tích khối tứ diện đều cạnh a.
Giải
Gọi tứ diện có cạnh a là ABCD.
Từ A vẽ đường cao AH. Ta có: H e (BCD)
Vì ABCD là tứ diện đều nên:
AABH = AACH = AADH
=> HB = HC = HD
Suy ra H là trọng tâm cũng đồng thời là tâm của tam giác đều BCD.
Khi đó BH = ị.ệ.a = và AH = y/a2 - BH2 = a.ỈỊ
3 2	3	V3
Vậy thể tích tứ diện đều ABCD cạnh bằng a là:
v4.SẠBCD.AH=l^.a^
Bài 2. Tính thể tích khối bát diện đều cạnh a.
Giải
Khối bát diện đều gồm hai khối chóp tứ giác đều bằng nhau. Trong hình bên, SO là chiều cao của khối chóp S.ABCD.
Khi đó SO = VsA2-OA2
Vì bát diện đều có cạnh a nên: so
Vậy thể tích của khối tám mặt đều cạnh a là:
1	 2 o aV2
V = 2. Vs.abcd =
2.^.Sabcd-SO = -^.a2.—
3
Bài 3. Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số giữa thể tích của khôi hộp đó và thể tích của khối tứ diện ACB’D’.
Giải
Gọi s là diện tích đáy và h là chiều cao của khối hộp.
A’	B’
Chia khối hộp thành tứ diện ACB’D’ và bôn khôi chóp A.A’B’D’, C.C’B’D’, B’.BAC, D’.DAC.
v. |sh
3
Bài 4. Cho khôi chóp S.ABC. Trên các đoạn thẳng SA, SB, sc lần lượt lấy ba điểm A’, B’, C’ khác với s. Chứng minh rằng:
Vsabv _ SA' SB' SC'
VS.ABC SA’SB’SC
Giải
Gọi H và K lần lượt là hình chiếu vuông góc của A và A’ trên mp(SBC), đặt AH = hi và A’K = h2, S1 và s2 lần lượt là diện tích của hai tam giác SBC và SB’C’, ta có:
h2 A’K SA'
h| AH " SA
x s, ỊsinB'SC .SB .se SB, sc,
S2 I sinBSC.SB.SC SB sc
2
U h
Vây VS.A'BC'- 3 2 2 _ h2 S2 _ SA'.SB'.SC'
VS.ABC ls,.h, hĩ’s> SA.SB.SC
3 '■ 1
Bài 5. Cho tam giác ABC, vuông cân ở A và AB = a. Trên đường thẳng qua c, vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua c vuông góc với BD cắt BD tại F và cắt AD tại E. Tính thể tích khôi tứ diện CDEF theo a.
Ta có:
BAI CD
BAI ca/
Giải
BA±(ADC)=>BA_LCE
(1)
Mặc khác: BD 1 (CEF) (giả thiết) => BD ± CE (2)
Từ (1) và (2) suy ra CE 1 (ABD)
Vậy CE 1 EF, CE 1 AD
Tam giác ACD vuông cân ở c và
CA = CD = a
Suy ra CE =
BC = ay/2, BD
= ặ/ EC2 + CD2 = aJ 2a2 + a2 = a^ã
Tam giác BCD vuông ở c và có đường cao CF nên
CF.BD = DC.BC CF =	= a. lị
BD aV3 V3
Ta có:
ef = Vcf2-ce2
DF = 7dC2-CF2
s _1CE.EF=-.-^.^	a2^
12
iCEF 2	2’ 2 ■ 6
Vậy thể tích của khối tứ diện DCEF là:
v = ■|SACEF-DF =	= ^7
3	3	3	3	36
Bài 6. Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Giải
C b Dd-
Gọi h là khoảng cách từ d đến d’ và a là góc tạo bởi d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE. Ta có ABE.CFD là một hình lăng trụ tam giác có chiều cao bằng h và a = BAE nếu BAE c 90° hoặc a = 180° - BAE nếu BAE > 90°.
Mặc khác: AE = CD = b
Ta có: Vabcd = Vdabe = “Vabe.cfd =— -S^ABE-h
= —AB.AE.sin BAE = -^-h.ab.since (không đổi).
3 2	6