Giải bài tập Toán 12 ÔN TẬP CHƯƠNG 1

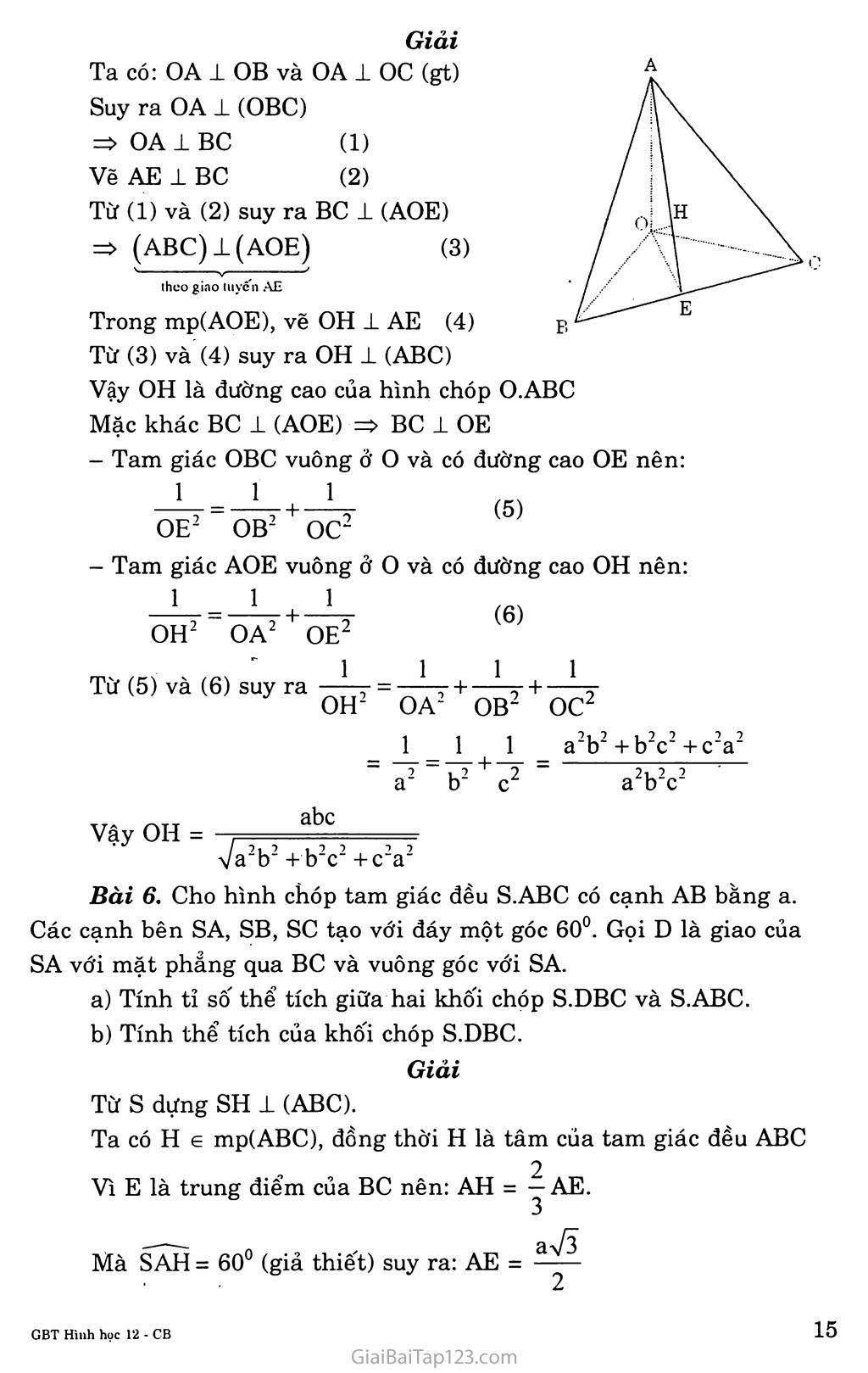
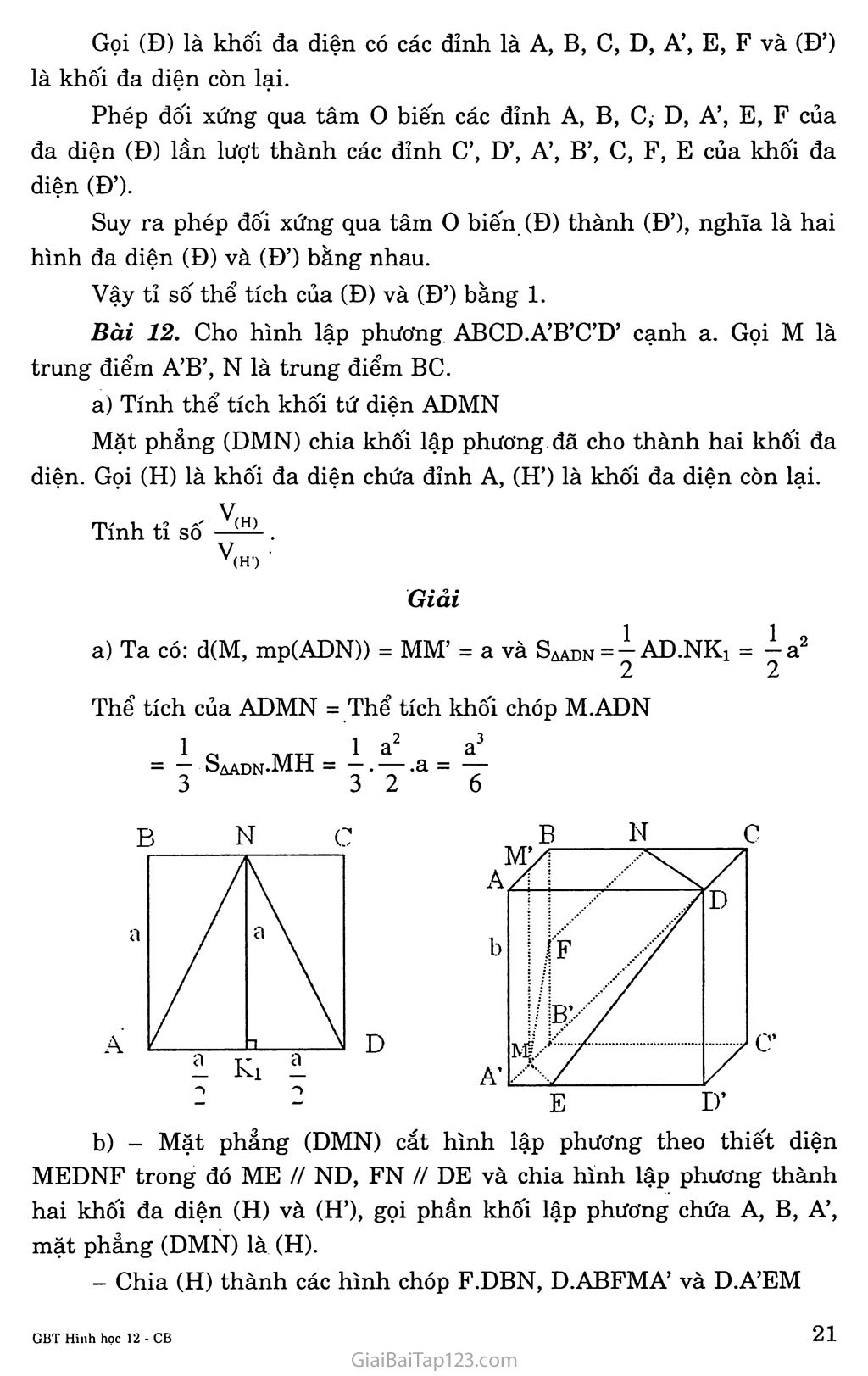
ÔN TẬP CHƯƠNG I
Bài 1. Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất nào ?
Giải
Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất:
Mỗi đỉnh là đĩnh chung của ít nhất ba cạnh, ba mặt;
Mỗi cạnh là cạnh chung của đúng hai mặt;
Hai mặt bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có đúng một cạnh chung.
Bài 3. Thế nào là một khối đa diện lồi. Tìm ví dụ trong thực tế mô tả một khối đa diện lồi, một khối đa diện không lồi.
Giải
Khôi đa diện lồi (khối chóp)
Với hai điểm M và N thuộc khối đa diện thì mọi điểm của đoạn thẳng MN cũng thuộc khối đa diện đó. Ta gọi đó là khối đa diện lồi.
Khối đa diện không lồi
Bài 4: Cho hình lăng trụ và hình chóp có diện tích đáy và chiều cao bằng nhau. Tính tĩ số thể tích của chúng.
Giải
Gọi s là diện tích đáy và h là chiều cao của hình lăng trụ và của hình chóp, ta có:
Thể tích khối lăng trụ là: V1 = Sh
Thể tích khôi chóp là: v2 = Ậsh
3
vậy “L = ~“ = 3
v2 Sh
Bài 5. Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, oc đôi một vuông góc với nhau và OA = a, OB = b, oc = c. Hãy tính đường cao OH của hình chóp.
Giải
Ta có: OA ± OB và OA 1 oc (gt) Suy ra OA ± (OBC)
theo giao tuyến AE
Trong mp(AOE), vẽ OH ± AE (4)
Từ (3) và (4) suy ra OH ± (ABC)
Vậy OH là đường cao của hình chóp O.ABC
Mặc khác BC ± (AOE) => BC 1 OE
Tam giác OBC vuông ở o và có đường cao OE nên:
111
OE2 OB2 + oc2
Tam giác AOE vuông ở o và có đường cao OH nên:
(6)
OH2 OA2 OE2
Từ (5) và (6) suy ra 1 =--■■■ + A _ \
OH2 OA2 OB2 oc2
_Ị_ = J_ 1 _ a2b2+b2c2+c2a2 a2 b2 c2 " a2b2c2
Vậy OH = abc
ựa2b2 + b2c2 +c2a2
Bài 6. Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, sc tạo với đáy một góc 60°. Gọi D là giao của SA với mặt phảng qua BC và vuông góc với SA.
Tính tỉ số thể tích giữa hai khối chóp S.DBC và S.ABC.
Tính thể tích của khối chóp S.DBC.
Giải
Từ s dựng SH 1 (ABC).
Ta có H 6 mp(ABC), đồng thời H là tâm của tam giác đều ABC ~	— 2
Vì E là trung điểm của BC nên: AH = Ỷ AE. Mà SAH = 60° (giả thiết) suy ra: AE = -ệ-
TTA A T T *" A D 2 a \ J a
Vậy AH - — AE = — . —— = —— 3	3	2	3
Mặc khác:
SH = AH.tanSAH = AH.tan60°
3
DE = AE.sin DAE = AE.sin60°
_ aV3 V| _ 3a
Ta CÓ ■
SA = 2AH = 2—7
3
SD = SA-AD = aV3
---i
3 4J
 aVj
5a\ố
12
2 ■ 2 " 4
a) Vậy tỉ số thể tích giữa hai khối chóp S.DBC và S.ABC là:
VS.DBC _ SD.SB.SC _ SD _ 5aV3 2aự3 _ 5
VSABC SA.SB.se" SA - 12 ' 3 _8
b) Thể tích của khôi chóp S.DBC là:
Thể tích của khối chóp S.ABC:
V.- 1	1 1 a^QQ_a’^
V1 = — Saabc-SH =	— .a.a - ■■
3	322	12
5
Thể tích S.DBC là v2 = ^.y =
8 1	96
Bài 7. Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA = 7a. Các mặt bên SAB, SBC, SCA tạo với đáy một góc 60°. Tính thể tích của khối chóp đó.
Giải
Từ s dựng SH 1 (ABC), H e mp(ABC), đồng thời dựng HE 1 AB,
HF 1 BC, HI 1 AC.
Ta có: SE 1 AB; SF 1 BC; SI 1 AC
Theo đề bài, góc hợp bởi (SAB), (SBC), (BAC), (SAC) và đáy (ABC) lần lượt là SEH = SFH = siH = 60°
=> ASHE = ASHF = ASHI
=> HE = HF = HI = r (vởi r là bán kính đường tròn nội tiếp tam giác ABC).
Chu vi tam giác ABC là 2p = 18a.
Theo công thức Hê-rông, diện tích tam giác ABC là:
s = ự9.4.3.2.a4 =6a2Vó
_ '	, __ s 2aVó
a CÓ công thức s = p.r, ta có r = — = —— p 3
=> SH = EH.tanSEH = r.tan60° = ^7^-73 = 2a7ĩ 3
Vậy thể tích S.ABC là:
v = ISaabc-SHzz |6.a2VÃ2aV2=8a3V3
3	3
Giải
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy và AB = a, AD = b, SA = c. Lấy các điểm B’, D’ theo thứ tự thuộc SB, SD sao cho AB’ vuông góc với SB, AD’ vuóng góc với SD. Mặt phẳng (AB’D’) cắt sc tại C’. Tính thể tích khối chop S.AB’C’D’.
* Ta có:
BC1SA
BC1AB
AB’l (SBC) => AB’ 1 sc AD’ 1 (SCD) => AD’ 1 sc
Mặc khác:
và
Từ (1) và (2) suy ra sc 1 (AB’Ơ)
* Ta lại có:
SB =7aB2+AS2 -7a2+c2;
SD = 7sA2+AC2 = 7c2 + AB2+AD2 - 7a2+b2+c2;
sc = 7a2+b2+c2.
Sasab = ị s A.AB = 1 AB' .SB AB' = -S^— = -T-Ca—; 2	2	SB 7777
c
ộ+b2+c2
1 2 c2a2
c	V—
Tương tự AD' = , b 5 AC' =
7b2+c2
+ b2
c2
Tương tự SD' = ,	—-,SC' =
Vb2+c2
B'C'
c2
^a2 +b2 +c2
SC' SB
bc2
BC.SC'
SB
Tương tự D'C' =
+b2+c2.7b2
ac2
+ b2 + c2 .Vb2 +c2 AB’ ± B’C’ và AD’ ± D’C’ nên: s =1 —1 c oaab'C’ 2
a2 +c:
1	abc3
) /„2
ca
7
Vì ASC’B’ ASBC nên
Tương tự: SAAƠC. -
Vậy thể tích hình chóp S.AB’C’D’ là:
abc3
1 abc5	a2+b2+2c2	_	abc5 (a2 +b2 +2c2)
6 a2+b2+c2 (a2+c2)(b2+c2) ó(a2 +c2)(b2 +c2)(a2 +b2 +c2)
c2
’n'^ + bW
V = —- Sab’C’d’-SC’ = —- (Saab’c’+Saad’C’I-SC 3	3
_ _1 J_ 	
Bài 9. Cho hình chóp tứ giác đều S.ABCD. Đáy hình vuông cạnh a, cạnh bên tạo với đáy một góc 60°. Gọi M là trung điểm sc. Mặt phẳng đi qua AM và song sohg với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khôi chóp S.AEMF.
Giải
Ta có <
ÍBD1AC nên BD 1 (SAC) => EF 1 (SAC)
BD1SO
Mà AM G (SAC) nên EF 1 AM
„	.2	2 a-x/2 aVĨ
Ta lại có: El = FI =	=
3	3 2	3
Và SCO là góc tạo bởi cạnh bên sc và đáy (ABC): SCO = 60°.
Vì SA = AC và SCO = 60° nên SAC là tam giác đều cạnh bằng a^2
2
Vì EF 1 AM nên S^p = I AM.EF = AM.EI =
6
3
SM thuộc (SAC) và EF 1 (SAC)
(1)
(2)
=> SM ỉ EF
SAC ]à tam giác đều nên SM ± AM
Từ (1) và (2) suy ra SM ± (AEMF). Điều này chứng tỏ SM là đường cao của hình chóp S.AEMF.
Vậy thể tích của khôi chóp S.AEMF là:
18
Bài 10. Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a.
Tính thể tích khối tứ diện A’BB’C’.
Giải
a) Thể tích khối tứ diện A’BB’C’ là:
Mặt phẳng đi qua A’B’ và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Tính thể tích hình chóp C.A’B’FE.
3’ 4 ■	12
b) Gọi I, K lần lượt là trung điểm của AB và A’B’, G là trọng tâm của tam giác ABC.
Đường thẳng qua G, song song với AB cắt AC và BC lần lượt tại E và F, đường thẳng EF chính là giao tuyến của hai mặt phẳng (GA’B’) và (ABC).
(1)
(2)
Ta có: <
Mặc khác EF // AB
Từ (1) và (2) suy ra EF 1 (CIKƠ) => (A’B’FE) 1 (CIKƠ).
Vậy khoảng cách từ c đến mp(A’B’FE) bằng khoảng cách từ c đến KG.
Ta có:
CI = -^, IG = ịci = ^
3	6
Suy ra KG = VlK2 + IG2
Sagkc= I IK.GC = ị .IK. Ị .CI = ị. ị .IK.CI = ị a.a^3
2	2	3	3 2	3
Khoảng cách từ c đến KG là d = 2SAGKC:
KG =
6 V 12	13
Đây cũng là khoảng cách từ c đến mp(A’B’FE)
Diện tích khối chóp C.A’B’FE là:
 	 1 6	2 'í	[13
S = 4(A'B + EF).KG) = 4 a + ịa .a.J^- =
2(	3 J V12
Thể tích khối chóp C.A’B’FE là:
v 1. d=l^ĩ
3’ A’B'FE- 3'12
3
5a3
18 Vã
Bài 11. Cho khôi hộp ABCD.A’B’C’D’. Gọi E và F theo thứ tự là trung điểm của các cạnh BB’ và DD’. Mặt phẳng (CEF) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khôi đa diện đó.
Giải
Gọi o là tâm hình hộp và tâm của hình bình hành BB’D’D. Khi đó o là trung điểm của EF.
Ta có: A’ G co
CO c mp(CEF)
(1)
(2)
Từ (1) và (2) suy ra A’ 6 mp(CEF).
Mặc khác A’E // CF, A’F // CE
Nên mp(CEF) cắt hình hộp theo thiết diện là hình bình hành A’ECF.
Mp(CEF) chia hình hộp ABCD.A’B’C’D’ thành hai khôi đa diện (Đ) và (Đ’).
Gọi (Đ) là khối đa diện có các đỉnh là A, B, c, D, A’, E, F và (Đ’) là khối đa diện còn lại.
Phép đối xứng qua tâm o biến các đỉnh A, B, c, D, A’, E, F của đa diện (Đ) lần lượt thành các đỉnh C’, D’, A’, B’, c, F, E của khối đa diện (Đ’).
Suy ra phép đôi xứng qua tâm o biến (Đ) thành (Đ’), nghĩa là hai hình đa diện (Đ) và (Đ’) bằng nhau.
Vậy tỉ số thể tích của (Đ) và (Đ’) bằng 1.
Bài 12. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm A’B’, N là trung điểm BC.
a) Tính thể tích khối tứ diện ADMN
Mặt phảng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A, (H’) là khối đa diện còn lại.
V
Tính tỉ sô' <H) .
	■
V(H')
Giải
a) Ta có: d(M, mp(ADN)) = MM’ = a và Saadn = ị AD.NK1 = ị a2
2	2
Thể tích của ADMN = Thể tích khôi chóp M.ADN
= 1 Saadn,MH = ị .ị
3	3 2
hình lập phương theo thiết diện
b) - Mặt phẳng (DMN) cắt
MEDNF trong đó ME // ND, FN // DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H).
- Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM
Ta CÓ: FN // ED => AFBN ^ADD’E
BF _DD’_4 _DC_4DXT_2~ =>	2 => BF = -7-BN = 2a
BN ED' 3	3	3
a2
Ta CÓ: Sadbn =
4
Thể tích của F.DBN là:
V 1C	_ 2 a2 2a _a3
a a a2 Bafmb’ =
2 3 12
2 |a3 Diện tích ngũ giác ABFMẠ’ = a2 - SAFMB' = -77-
36
111a2	1 la3
Thể tích của D.ABFMA’ là Vdabfma’ = T-^.a = ~
12	36
a a a2 Ba’me =
2 4 16
Thể tích của A.A’ME là:
1	- 1 a2 a2
Vd.a’me = — -Saa’me-DD’ = —.a = —
3	2 16	48
Thể tích của (H) là: Vj =	1 la a 55a
18
Thể tích của (H’) là: v2 = a3
Vậy tỉ số thể tích là k = ——
V...
36 48 144
55a3 _ 89a3
144 " 144
55
89