Giải toán 12 Bài 1. Khái niệm về khối đa diện

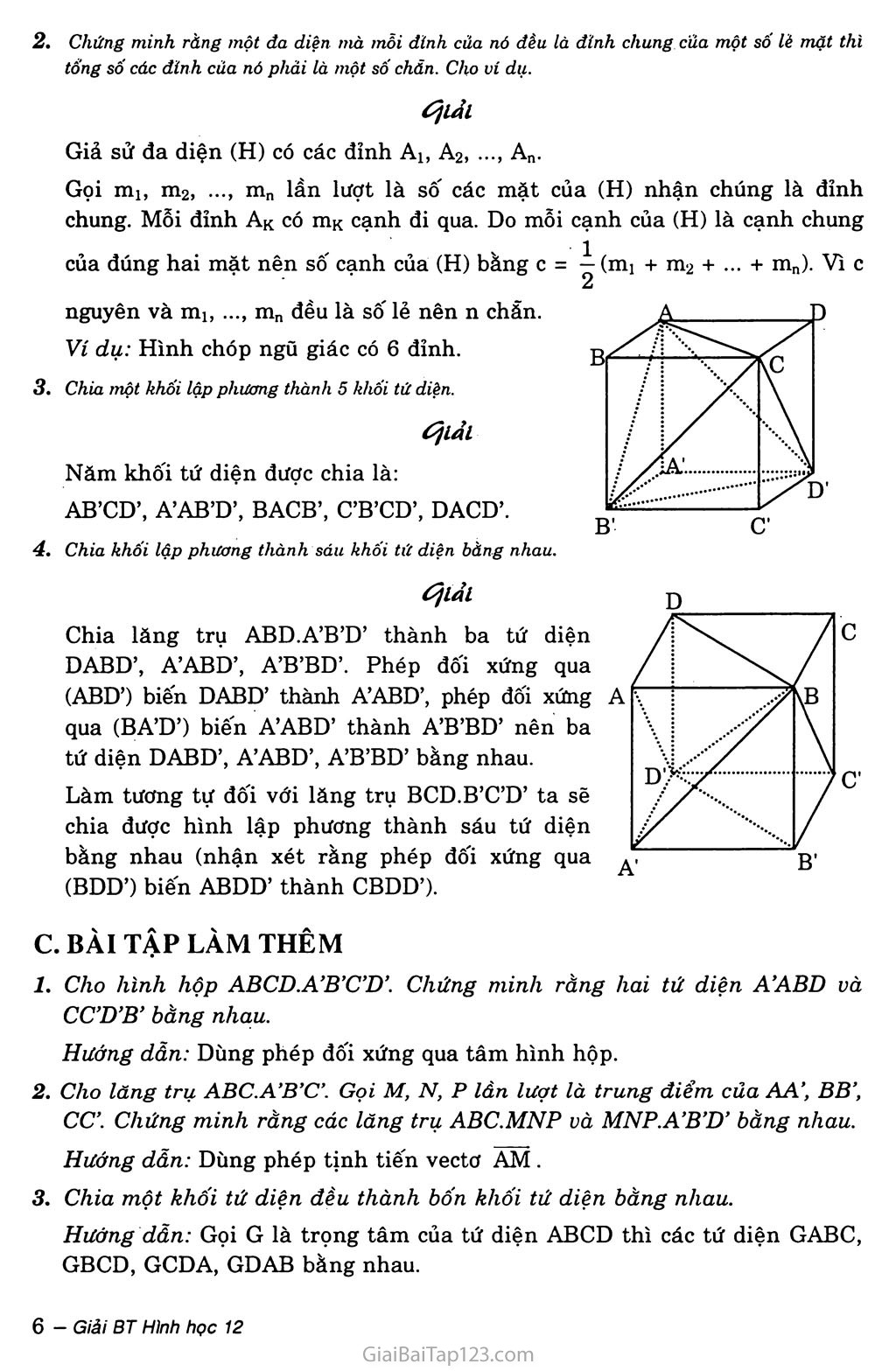
§1. KHÁI NỆM VỀ KHỐI ĐA DIỆN
A. KIẾN THỨC CĂN BẢN
KHỐI LĂNG TRỤ VÀ KHỐI CHÓP
Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy. Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHÔÌ ĐA DIỆN
Khái niệm về hình đa diện
Hai đa giác phân biệt chỉ có thể hoặc không có một điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Khái niệm vể khối đa diện
Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
HAI ĐA DIỆN BẰNG NHAU
Phép dời hình trong không gian
Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M' xác định duy nhất được gọi là một phép biến hình trong không gian. Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
Các phép dời hình trong không gian: Phép tịnh tiến theo vectơ V, phép đối xứng qua mặt phẳng (P), phép đối xứng qua đường thẳng A, phép đối xủng tâm o.
Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Chứng minh ràng một đa diện có các mặt là những tam giác thì tổng sô các mặt của nó phải là một sô chẵn. Cho vi dụ.
Ốịiải
Giả sử đa diện (H) có n mặt. Mỗi mặt của (H) có 3 cạnh nên n mặt có 3n cạnh. Vì mỗi cạnh của (H) là cạnh chung của đúng hai mặt nên sô" cạnh
của (H) bằng do đó n là sô" chẵn. Ví dụ: Tứ diện có 6 cạnh.
2
Chứng minh ràng một đa diện mà mỗi dính của nó đều là đính chung của một sô' lẻ mặt thì tổng số các đỉnh của nó phăi là một số chẵn. Cho ví dụ.
6jlải
Giả sử đa diện (H) có các đỉnh Ai, A2, An.
Gọi mb m2, mn lần lượt là số các mặt của (H) nhận chúng là đỉnh chung. Mỗi đỉnh AK có mK cạnh đi qua. Do mỗi cạnh của (H) là cạnh chung
của đúng hai mặt nên số cạnh của (H) bằng c =	(m, + m2 + ... + mn). Vì c
2
nguyên và mb ..., m„ đều là sô' lẻ nên n chẵn.
Ví dụ: Hình chóp ngũ giác có 6 đỉnh.
Chia một khối lập phương thành 5 khối tứ diện.
Năm khôi tứ diện được chia là:
AB’CD’, A’AB’D’, BACB’, C’B’CD’, DACD’.
Chia khối lập phương thành sáu khối tứ diện bàng nhau.
Ốjlảt
Chia lăng trụ ABD.A’B’D’ thành ba tứ diện DABD’, A’ABD’, A’B’BD’. Phép đối xứng qua (ABD’) biến DABD’ thành A’ABD’, phép đối xứng A qua (BA’D’) biến A’ABD’ thành A’B’BD’ nên ba tứ diện DABD’, A’ABD’, A’B’BD’ bằng nhau.
Làm tương tự đối với lăng trụ BCD.B’C’D’ ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau (nhận xét răng phép đô'i xứng qua (BDD’) biến ABDD’ thành CBDD ).
c. BÀI TẬP LÀM THÊM
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai tứ diện AABD và CC’D’B’ bằng nhau.
Hướng dẫn: Dùng phép đốì xứng qua tâm hình hộp.
Cho lăng trụ ABC.A’B’C’. Gọi M, N, p lần lượt là trung điểm của AA’, BB’, CC’. Chứng minh rằng các lăng trụ ABC.MNP và MNP.A’B’D’ bằng nhau. Hướng dẫn: Dùng phép tịnh tiến vectơ AM .
Chia một khối tứ diện đều thành bốn khối tứ diện bằng nhau.
Hưởng dẫn: Gọi G là trọng tâm của tứ diện ABCD thì các tứ diện GABC, GBCD, GCDA, GDAB bằng nhau.