Giải toán 12 Bài 2. Khối đa diện lồi và khối đa diện đều

§2. KHỐI ĐA DIỆN Lồi VÀ KHốI ĐA DIỆN ĐÊU
A. KIẾN THỨC CĂN BẢN
Khối đa diện lồi
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
Khối đa diện đều
Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
Mỗi mặt là một đa giác đều có p cạnh
Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}
Định lí: Chỉ có 5 loại khối đa diện đều. Đó là loại {3; 3}, loại {4; 3}, loại {3; 4}, loại {5; 3} và loại {3; 5}.
Bảng tóm tắt của năm loại khối đa diện đều:
Loại
Tên gọi
Số đỉnh
Số cạnh
Số mặt
{3; 3}
Tứ diện đều
4
6
4
{4; 3}
Lập phương
8
12
6
{3; 4}
Bát diện đều
6
12
8
{5:3}
Mười hai mặt đều
20
30
12
{3:5}
Hai mươi mặt đều
12
30
20
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
1. cắt bìa theo mầu dưới đây (hình vẽ), gâ'p theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều, hình lập phương và hình bát diện đều.
Hướng dẫn: Khi cắt theo hình đã cho cần chừa các mép để có thể dán lại với nhau.
Cho hình lập phương (H). Gọi (H') là hình bát diện đều có các đính là tâm của các mặt cứa (H). Tínli ti số diện-tích toàn phần của (H) và (H').
ỐỊlảl
Gọi a là độ dài cạnh hình lập phương (H) thì độ dài cạnh hình bát diện đều (H’) là
. Diện tích toàn phần của (H) là 6a2. 9
Diện tích mỗi mặt của (H’) là: s = f a^ì 7ỊE - a yã l 2 J 4	8
	 _	.	 „2/5
Diện tích toàn phần của (H’) là: 8. —= a27Õ
B
D
D
Vậy tỉ số diện tích toàn phần của (H) và (H’) là: 6a2: a273 = -^ = 273.
73
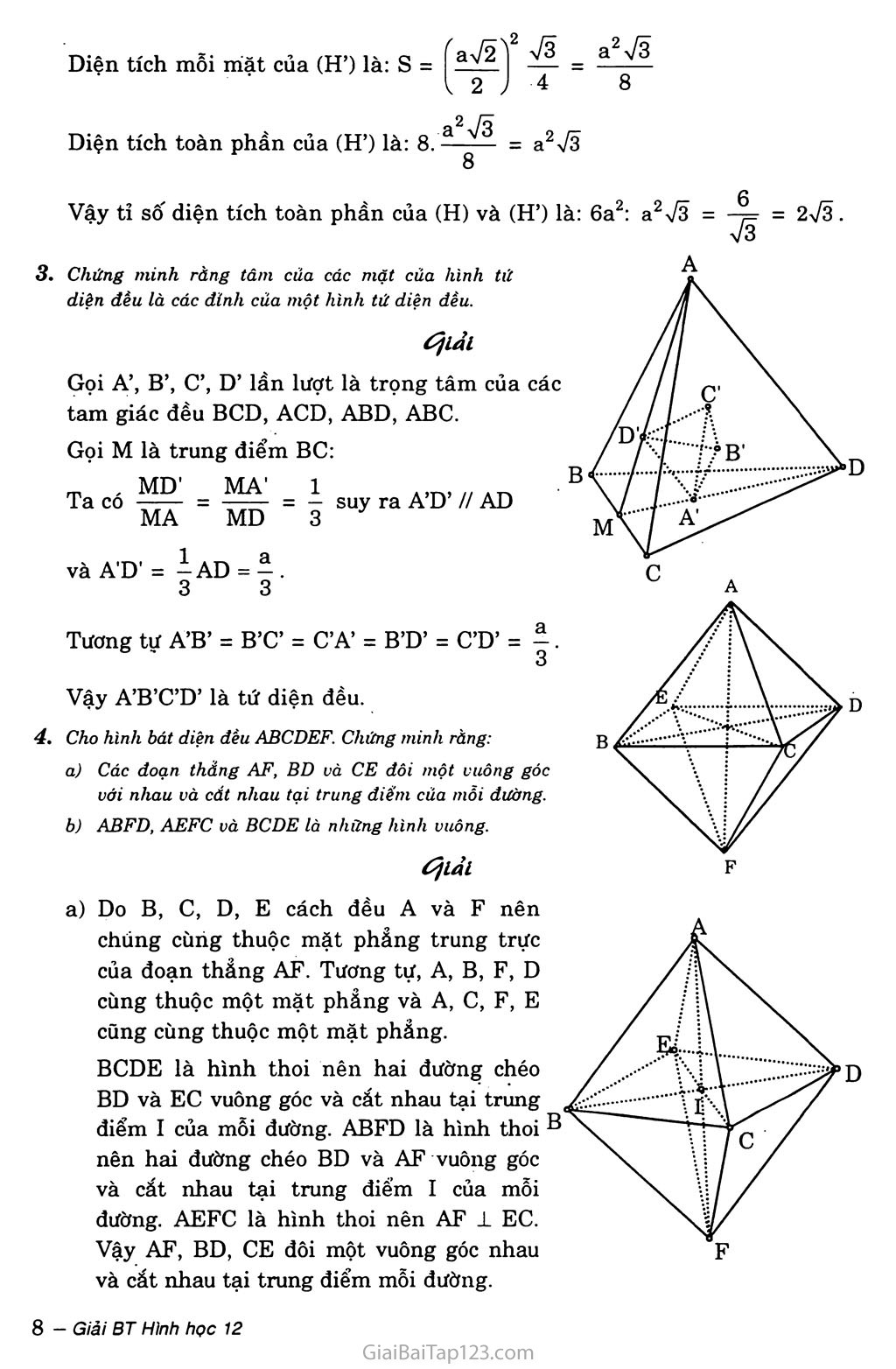
Chứng minh ràng tâm của các mặt của hỉnh tứ diện đều là các dinh của một hình tứ diện đều.
éjiải
Gọi A’, B’, C’, D’ lần lượt là trọng tâm của các tam giác đều BCD, ACD, ABD, ABC.
Gọi M là trung điểm BC:
, MD’ _ MA' _ 1 _ _	„ AT^
Ta có -7-T— = -7777 = 77 suy ra A D’ // AD MA MD 3
và AD' = ỈAD = ^.
3	3
Tương tự A’B’ = B’C’ = C’A’ = B’D’ = C’D’ = ị.
3
Vậy A’B’C’D’ là tứ diện đều.
Cho hình bát diện đều ABCDEF. Chứng minh rằng:
Các doạn thẳng AF, BD và CE dôi một vuông góc với nhau và cắt nhau tại trung điểm của mồi đường.
ABFD, AEFC và BCDE là những hình vuông.
ố^iải
a) Do B, c, D, E cách đều A và F nên chúng cùng thuộc mặt phẳng trung trực của đoạn thẳng AF. Tương tự, A, B, F, D cùng thuộc một mặt phẳng và A, c, F, E cũng cùng thuộc một mặt phẳng.
BCDE là hình thoi nên hai đường chéo BD và EC vuông góc và cắt nhau tại trung điểm I của mỗi đường. ABFD là hình thoi B nên hai đường chéo BD và AF vuông góc và cắt nhau tại trung điểm I của mỗi đường. AEFC là hình thoi nên AF 1 EC.
Vậy AF, BD, CE đôi một vuông góc nhau và cắt nhau tại trung điểm mỗi đường.
b) Do AI 1 (BCDE), AB = AC = AD = AE nên IB = IC = ID - IE. Từ đó suy ra BCDE là hình vuông. Tương tự ABFD, AEFC là những hình vuông.
c. BÀI TẬP LÀM THÊM
Chứng minh rằng tăm các mặt cúa hình bát diện đều là các đỉnh của một hình lập phương.
Cho khối bát diện đều ABCDEF cạnh a. gọi o là giao điểm của AC và BD, I và J lần lượt là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát diện với mp (OIJ)
r)' on.	„2
iJap so:	a .