Giải toán 12 Ôn tập chương I
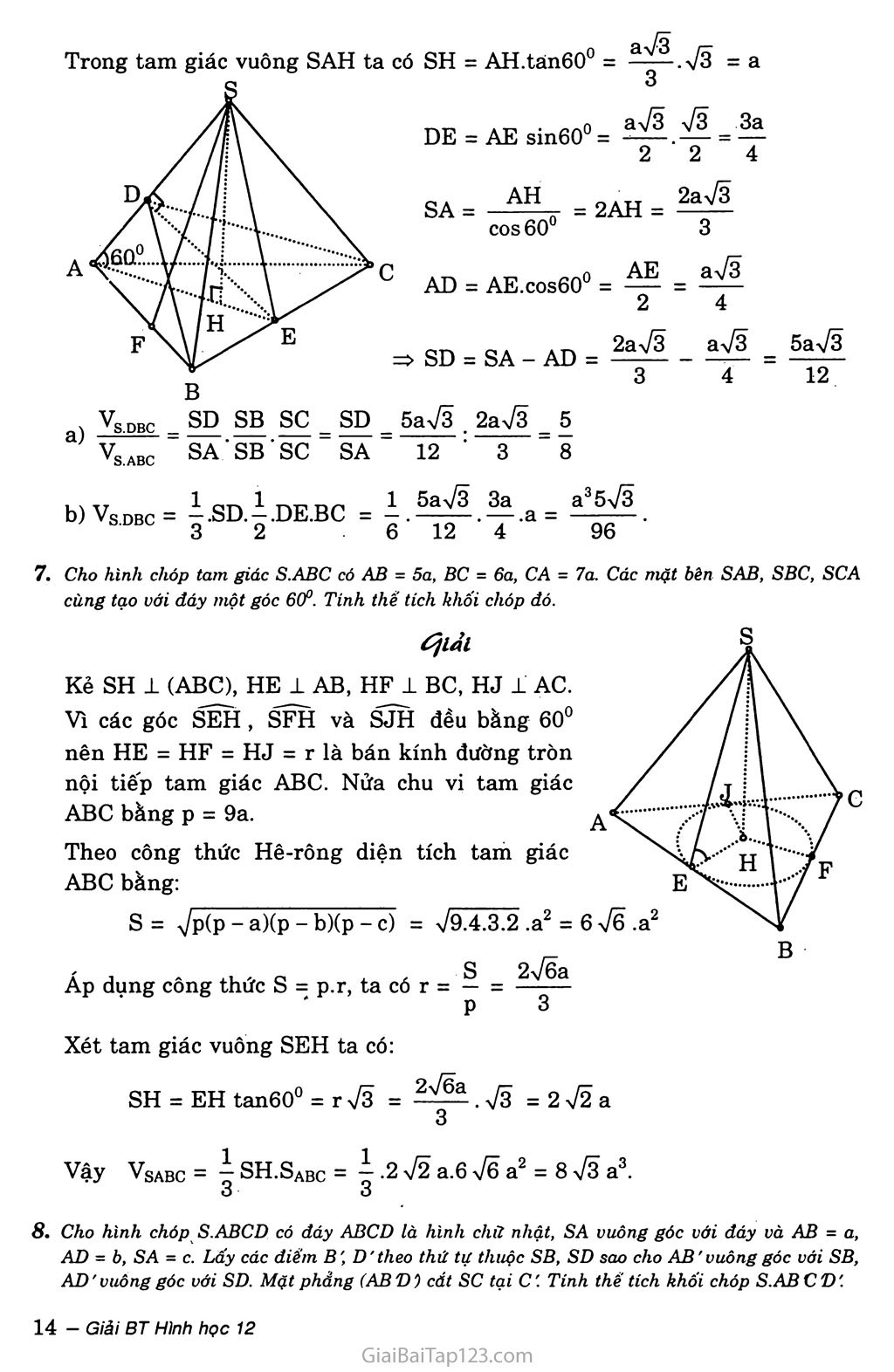
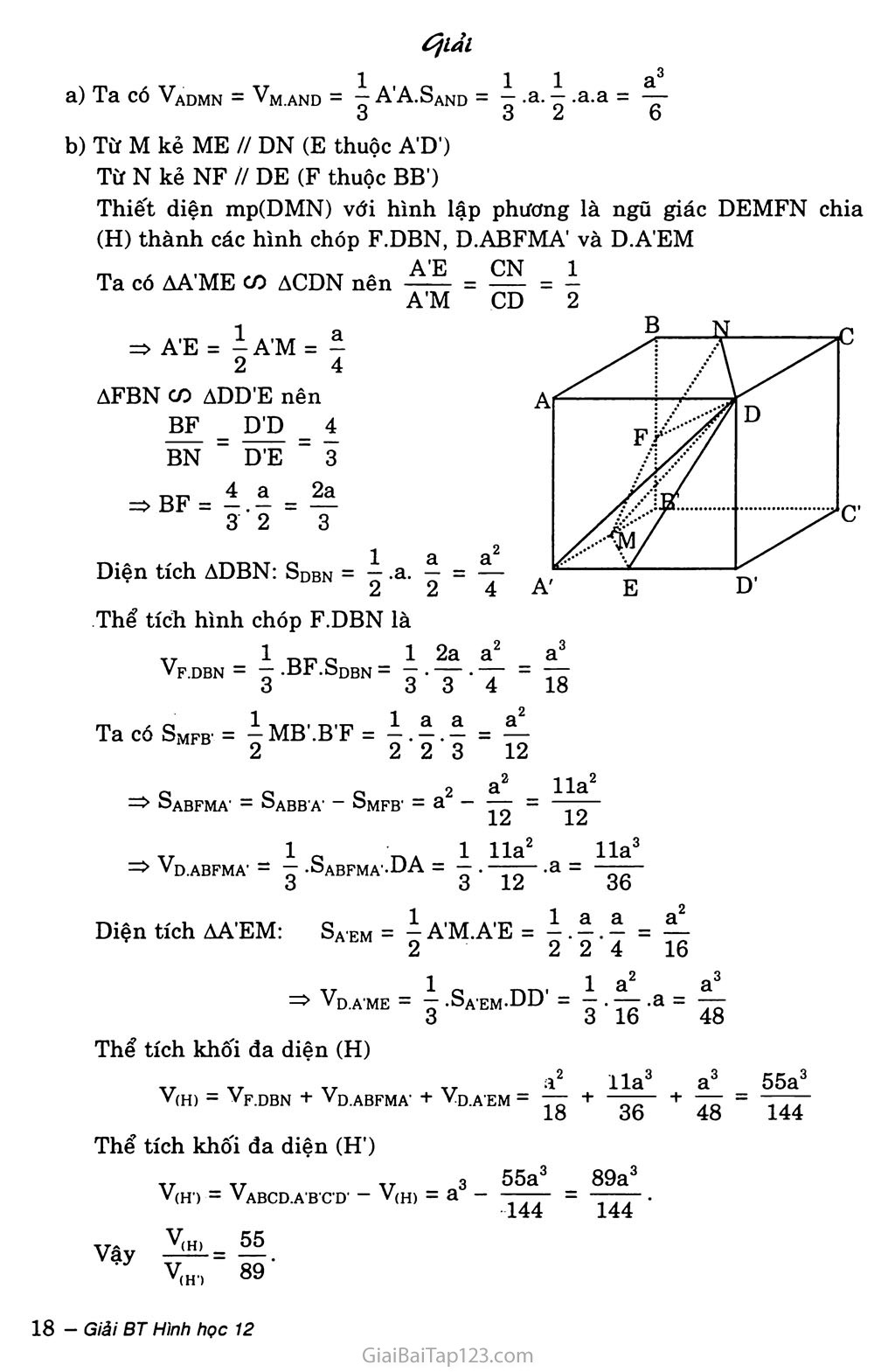
ÔN TẬP CHƯƠNG I Cho hình lăng trụ và hỉnh chóp có diện tích đáy và chiều cao bằng nhau. Tính tt sô thế tích cúa chúng. Ốịiảl Giả sử hình lãng trụ và hình chóp lần lượt có thể tích là V! và v2. Có diện tích đáy s và chiều cao h. Ta có V! = s.h; v2 = I s.h. 3 Suy ra = 3. Cho hỉnh chóp tam giác O.ABC có ba cạnh OA, OB, oc đôi một vuông góc nhau và OA = a, OB = b, oc = c. Hãy tính độ dài đường cao OH của hình chóp. OE2 OA2 + OB2 a2 + b2 OH là đường cao tam giác vuông OCE nên: 1 - 1 4- 1 - 1 + 1 + 1 OH2 " OE2 + oc2 " a2 + b2 + c2 1 _ - a'h2 +h'a2 + c2*2 m - abc OH2 a2b2c2 7a2b2 + b2c2 + c2a2 ' Cho hình chóp tam giác đểu S.ABC có cạnh AB bàng a. Các cạnh bên SA, SB, sc tạo với đáy một góc 6ũP. Gọi D là giao điếm của SA với mặt phăng qua BC và vuông góc với SA. Tính tỉ số thể tích của hai khối chóp S.DBC và S.ABC. Tính thề tích của khối chóp S.DBC. ốỊiải Gọi E là trung điểm BC. H là tâm tam giác đều ABC thì SH ± mp(ABC) ATT 2 , _ 2 a 73 aự3 Ta có AH = 77 AE = 77 = -77- 3 3 2 3 SAH = 60° là góc giữa cạnh bên SA với mp(ABC). ) VS.DBC _ SD SB SC _ SD 5aV3 . 2 a Tã 5 a vIabc ” SA ■ SB ' sc - SA “ 12 : 3 " 8 s B u\ AZ — 1 cn 1 TAT? Df _ 1 5 a 73 3a a3573 b) Vs.DBC = — .SD. —.DE.BC = — ■ ' . — .a = ——7—. 3 2 6 12 4 96 Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA - 7a. Các mặt bên SAB, SBC, SCA cùng tạo với đáy một góc 6ũP. Tinh thể tích khối chóp đó. Ốịiảl Kẻ SH 1 (ABC), HE 1 AB, HF 1 BC, HJ i AC. Vì các góc SEH , SFH và SJH đều bằng 60° nên HE = HF = HJ = r là bán kính đường tròn nội tiếp tam giác ABC. Nửa chu vi tam giác ABC bằng p = 9a. A Theo công thức Hê-rông diện tích tam giác ABC bằng: s = 7p(p - a)(p - b)(p - c) = 79.4.3.2 .a2 = 6 Tẽ ,a2 Áp dụng công thức s = p.r, ta có r = — = p 3 Xét tam giác vuông SEH ta có: SH = EH tan60° = r 73 = ^^.73 = 272a 3 Vậy VgABC = — SH.Sabc = — .2 72 a.6 7Õ a2 = 8 73 a3. o O Cho hình chóp S.ABCD có đáy ABCD là hỉnh chữ nhật, SA vuông góc với đáy và AB = a, AD = b, SA = c. Lấy các điểm B', D'theo thứ tự thuộc SB, SD sao cho AB'vuông góc với SB, AD'vuông góc với SD. Mặt phẳng (AB'D') cát sc tại c. Tinh thể tích khối chóp S.ABCD'. ỐỊiảl Gọi o là tâm hình chữ nhật ABCD, I là giao điểm của SO và B’D’ thì C’ là giao điểm của đường thẳng AI với sc. Ta CÓ IbC í AB = BC 1 O1 2-/Õ „3 /Õ Ta có: Va.bbc = Va.b'C'c = Vc.AB'C' = “■ Vabc.ab'C’ = „ -a mp(SAB) => BC 1 AB'. Mà AB' 1 SB nên AB’ 1 (SBC) => AB’ 1 sc. Tương tự AD' 1 sc Vậy SC 1 (ABTV). Ta có: SB = Va2 + c2 , SD = Vb2 + c2 , sc = Va2 + b2 + c2 Trong tam giác SAB, ta có SA.AB = AB'.SB => AB' = cb . cựa2 + b2 SA.AB SB ca a2 + c2 Tương tự Suy ra Tương tự AD' = . ; ; AC = - ... Va2 + c2 Va2 + b2 + c2 SB' = VSA2-AB'2 = ic2--^^ = V a2 + c2 c2 c2 SD' = ; sơ = -7-—-—- Vb2 + c2 Va2 + b2 + c2 Va2 + c2 Ta có ASCB' co ASBC nên ; SC' = B'C' BC B'C' = BC.SC' sc 7a2+b2+c2 SC' SB bc2 Va2 + b2 + c2 .Va2 + c2 Tương tự: D'C' = ac Va2 + b2 + c2 .Vb2 + c2 Vì AB' 1 B'C' và AD' 1 D'C', nên ta có: Sabc = ị B'C'AB' = ị -rỉ— b. ^=== 2 2 77+c2 Va2 +b2 +c2 Va2 +c2 abc3 ca abc3 2 (a2 + c2)Va2 +b2 +c2 Tương tự: Sađc = 1 „ /——— - 2 (b2 + c2)ựa2 + b2 + c2 Từ đó suy ra thể tích khối chóp phải tìm bằng: abc3 3 2 7a2 + b2 + c2 la2+c2 b2+c2J Va2 + b2 + c2 1 abc5 a2 + b2 + 2c2 abc6(a2 + b2 + 2c2) ■ 6 a2 + b2 + c2 (a2 + c2)(b2 + c2) " 6(a2 + c2)(b2 + c2)(a2 + b2 + c2) 9. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60°. Gọi M là trung điếm của sc. Mặt phảng đi qua AM và song song với BD, cắt SB tại E và cắt SD tại F. Tính thề tích của khối chóp S.AEMF. úịiắl Gọi o là tâm hình vuông ABCD, I là giao điểm của AM và so thì EF qua I và song song với BD. ĨbdĨac BD 1 (SAC) Ta có [BD 1 SO EF 1 (SAC) EF 1 AM SI I là trọng tâm tam giác SAC nên - SO Trong ASBD EF // BD nên = BD SO Vì SAO = SCO = 60° nên ASAC là tam giác đều cạnh a Vỗ do đó: AM = aV2.^ = 2 2 Diện tích tứ giác có hai đường chéo vuông góc AEMF là Saemf= |aM.EF= i.^.|aV2 = Zl Zl Ổ !Vã Ta có SC 1 EF (vì EF 1 (SAC)) SC 1 AM (vì ASAC đều) SC 1 (AEMF) Vậy SM = I sc = 2 2 V _ _ — Q1\4 <3 _ 1 aV2 a V3 a3 Vẽ Vs.AEMF = - .BM.SaEMF = - ■ —• —ỹ- = Cho lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh bằng a. Tinh thề tích của khối tứ diện A'BB'C. Mặt phẳng (P) đi qua AB' và trọng tâm tam giác ABC, cát AC và BC lần lượt tại E và F. Tính thể tích của hình chóp C.AB'FE. rp , T J 1 Z1T 1 a7"3 ãy/s Ta có IJ = •£- CI = -T —7— = —r- Cho hình hộp ABCD.AB'C’D’. Gọi E và F theo thứ tự là trung điểm của các cạnh BB', DD'. Mặt phẳng (CEF) chia khối hộp thành hai khối đa diện. Tính ti sô' thể tích của hai khôi đa diện đó. Ốịlảl Gọi o là tâm hình hộp. Khi đó o cũng là tâm của hình bình hành BB'DD'. Do đó 0 là trung điểm của EF. Do A' thuộc đường thẳng CO nên A' thuộc mặt phẳng (CEF). Ta có A'E H CF, AF // CE. Vậy mặt phăng (CEF) cắt hình hộp theo thiết diện là hình bình hành AECF. Mặt phẳng (CEF) chia hình hộp ABCD.A'B’C'D' thành hai hình đa diện (H) và (H'). Gọi (H) là đa diện có các đỉnh là A, B, c, D, A', E, F, (H') là đa diện còn lại. Phép đổì xứng qua tâm 0 biến các đỉnh A, B, c, D, A', E, F của đa diện (H) theo thứ tự thành các đỉnh c, D', Ạ', B1, c, F, E của đa diện (H1). Từ đó suy ra phép đốì xứng qua tâm 0 biến (H) thành (H'). Do đó hai hình đa diện (H) và (H') bằng r.hau. Suy ra tỉ số thể tích của chúng bằng 1. 72. Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M là trung điểm A'B', N là trung điểm BC. Tinh thể tích khối tứ diện ADMN. Mặt phẳng (DMN) chia khối lập phương dã cho thành hai khối da diện. Gọi (H) là V khối đa diện chứa đính A và (H') là khối da diện còn lại. Tinh tí số . tfiai 11a 3 12 36 Ta CÓ Vadmn = Vm.and = 7? A’A.Sand = o a o aa = 3 3 2 6 Từ M kẻ ME // DN (E thuộc A'D') Từ N kẻ NF // DE (F thuộc BB') Thiết diện mp(DMN) với hình lập phương là ngũ giác DEMFN chia (H) thành các hình chóp F.DBN, D.ABFMA' và DA’EM Ta có AA'ME co ACDN nên —— : A'M => A'E = ị A'M = Ị 2 4 AFBN CO ADD'E nên BF _ D'D 4 BN “ D'E " 3 => BF = = ậ 3 2 3 Diện tích ADBN: SDBN = .a. = 2 Thể tích hình chóp F.DBN là CN 1 V, F.DBN _ I = i 2a íỉ = — — .SnRW — — • ~7" - “7 3 3 4 18 Ta có SMFB' = ị MB'.B'F = 4 . = ị- JABFMA' ABBA' Smfb' = a2 - 12 lla 12 2 2 2 3 12 Thể tích khôi đa diện (H) a2 lla3 V(H) = Vp.DBN + VD.ABFMA' + VD.A'EM - 77 + 18 36 Thể tích khôi đa diện (H') 55a3 144 3 55a3 _ 89a3 Diện tích AA’EM: o 1 A'H< AtTC laa a Sa'em = „ A M.A E = — 2 2 2 4 16 V 1 Q nn' - 1 ậL Q - Vđ.ame = —-Saem-Uư = — . — a = — 3 16 48 48 Vậy V<H', = V, V, V, (H) (H) ABCD.ABCD' 55 89' V(H) = a: 144 144 w _ 1 c TA A _ 1 lla „ _ lla VD.ABFMA' = — .OABFMA-UA = — ■ .a = ——-