Giải Toán 10: Bài tập tổng hợp bổ sung

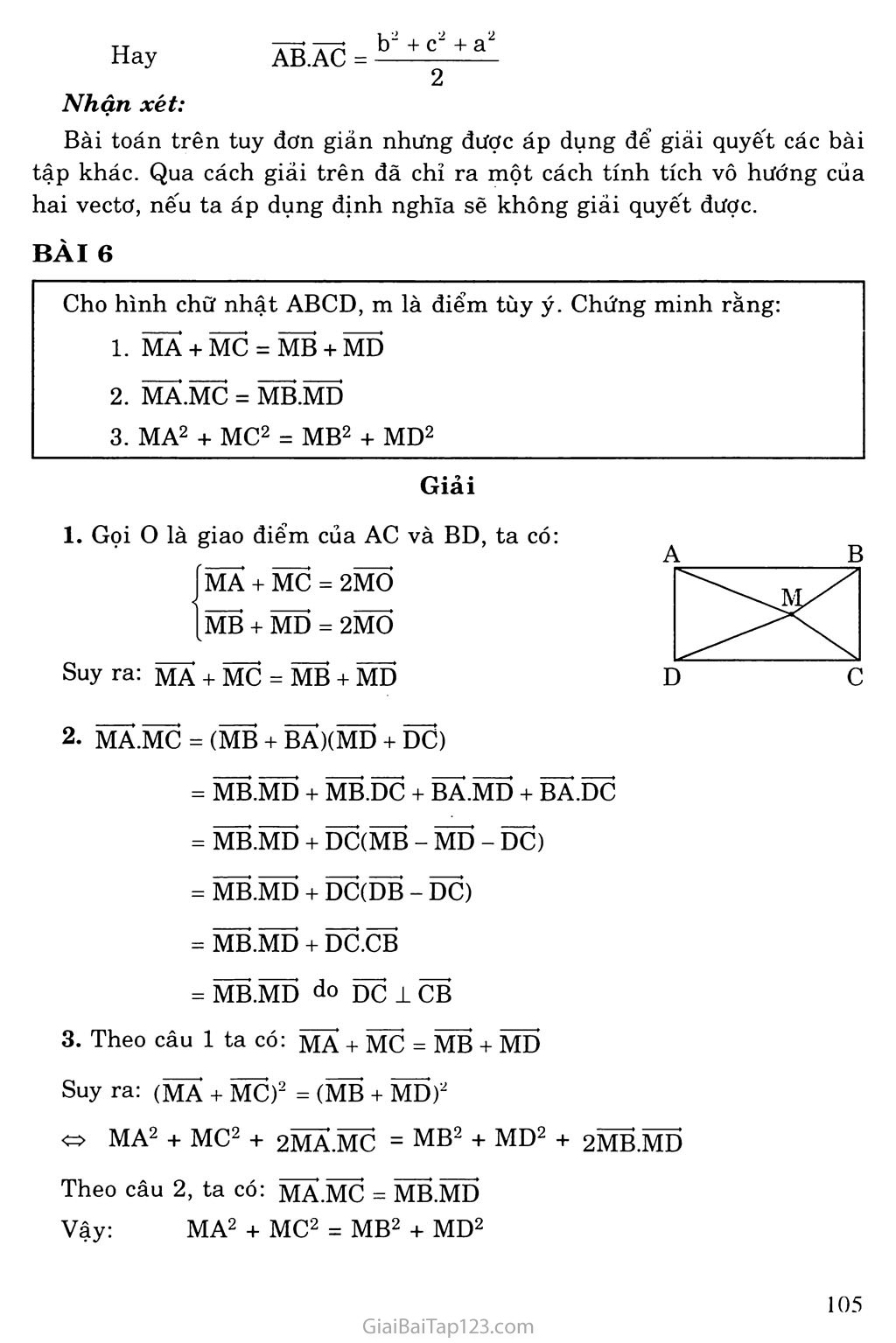
BÀI TẬP TỔNG HỢP Bổ SUNG
BÀI 1
Cho tam giác ABC và A’B’C’ có trọng tâm lần lượt là G và G’.
Chứng minh rằng: GG' = ■|(AA' + BB' + CC)
1	Oi-i	1
Ta có:	ÃÃT' = ÃG + GG*' + cTT'
BẼf = BG + Gcf’ + G’B'
ccf’ = CG + GG' + (Tc'
Cộng từng vế ba đẳng thức trên ta được:
ÃÃT' + BĨT + CCT' = -(GA + GB + GC) + 3GCC + (G^'' + Gt'' + G'c'') Do G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’ nên ta có:
GA + GB + GC = õ G'A' + G'B'' + G'C; = õ
Suy ra: ÃÃT' + BẼT' + cep = 30cf (đpcm)
Chú ý:
Từ bài tập trên ta suy ra kết quả sau đây: hai tam giác ABC và A’B’C’ có cùng trọng tâm khi và chỉ khi:
ÂT' + BẼT' + ecT' = õ
BÀI 2
Cho lục giác ABCDEF. Gọi M, N, p, Q, R, s lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng tam giác MPR, NQS có cùng trọng tâm.
Giải
Cách 1:
Giả sử G là trọng tâm tam giác MPR, khi đó ta có:
GN + GQ + GS =
= 4(GB + GC) + i(GD + GE) + i(GF + GA)
.	2	2	2	E Q D
= 4 (AC + CE + EA) = Õ 2
Vậy MN + PQ + RS = Õ • Do đó theo kết quả bài tập trên suy ra (đpcm).
BÀI 3
Cho tam giác ABC, gọi o, G, H theo thứ tự là tâm đường tròn ngoại tiếp, trọng tâm, trực tâm của tam giác ABC.
Chứng minh rằng:
ÕA + ÕB + ÕC = ÕH = 3ÕG
HA + HB + HC = 2HO = 3HG
Giải
Gọi A’ là điểm đối xứng của A qua o. Ta có BHCA’ là hình bình hành. Gọi D là trung điểm của BC (D là giao điểm của BC và HA’).
Ta có:	ÕB + ÕC = 2ÕD
Mặt khác OD là đường trung bình của AHAA’ nên OD = — AH 2
Suy ra:	ÕB + Õc = ÃH
=> ÕB + ÕC = ÕH-ÕÃ => ÕẨ + ÕB + ÕC = ÕH
Mặt khác theo tính chất trọng tâm, ta có:
ÕẨ + ÕB + Õc = 3ÕG
Theo tính chất trọng tâm, ta có:
HA + HB + HC = 3HG
Mà 3HG = 3HO + 3ÕG = 3HO + Õĩỉ = 2HO Vậy HA + HB + HC = 2HO = 3HG
BÀI 4
Chứng minh với bốn điểm A, B, c, D bất kì, ta có:
DA.BC + DB.CA + DC.AB = 0	(*)
Giải
Biến đổi các vectơ có mặt trong (*) thành các vectơ có cùng điểm đầu là D.
VT (*) = da.(DC - DB) + DB.(DA - DC) + DC.(DB - DA)
= DA.DC - DA.DB + DB.DA - DB.DC + DC.DB - DC.DA = 0
Nhận xét:
Xét AABC với D là giao điểm của hai đường cao AA’, BB’. Dựa vào (*) ta suy ra ba đường cao của AABC đồng qui.
BÀI 5
Cho tam giác ABC. Biết AB = c, BC = a, CA = b. Hãy tính AB.AC theo a, b, c.
Giải
Ta có:	BC = AC-AB
Vậy:	BC2 = (Ãc - ÃB)2
. BC2 = AC2 + AB2 - 2 ÃB.ÃC
TZi AB2 + AC2 - BC2 AB.AC =	—7”	
Hay	ÃB.ÃC = b" + c2 + a2
2
Nhận xét:
Bài toán trên tuy đơn giản nhưng được áp dụng đế giải quyết các bài tập khác. Qua cách giải trên đã chỉ ra một cách tính tích vô hướng của hai vectơ, nếu ta áp dụng định nghĩa sẽ không giải quyết được.
BÀI 6
Cho hình chữ nhật ABCD, m là điểm tùy ý. Chứng minh rằng:
MA + MC = MB + MD
MA.MC = MB.MD
MA2 + MC2 = MB2 + MD2
Giải
Gọi o là giao điểm của AC và BD, ta có: MA + MC = 2MO MB + MD = 2MO
Suy ra: MA + MC = MB + MD
MA.MC = (MB + BAXMD + DC)
= MB.MD + MB.DC + BA.MD + BA.DC = MB.MD + DC(MB - MD - DC)
= MB.MD + DC(DB - DC)
= MB.MD + DC.CB = MB.MD do DC 1 CB
Theo câu 1 ta CÓ: MA + MC = MB + MD
Suy ra: (MA + MC)2 = (MB + MD)2
 MA2 + MC2 + 2MA.MC = MB2 + MD2 + 2MB.MD
Theo câu 2, ta CÓ: MA.MC = MB.MD
Vậy:	MA2 + MC2 = MB2 + MD2
BÀI 7
Cho tam giác ABC có trọng tâm G. Chứng minh:
G A2 + GB2 + GC2 = — (a2 + b2 + c2)
MA2 + MB2 + MC2 = GA2 + GB2 + GC2 + 3MG2
Giải
Gọi G là trọng tâm của AABC nên ta có:
GA + GC + GC = õ (GA + GC + GC)2 = 0
=> GA2 + GB2 + GC2 + 2(GA.GB + GB.GC + GC.GA) =0 (1)
(GÃ - GB)2 = GA2 + GB2 - 2GA.GB
=> 2GA.GB = GA2 + GB2 - AB2 Tương tự: 2GB.GC = GB2 + GC2 - BC2
2GC.GA = GC2 + GA2 - AC2
Thay vào (1) ta được:
GA2 + GB2 + GC2 = |(a2 + b2 + c2)
O
Chú ý: Gọi ma, mb, mc là độ dài các đường trung tuyến của AABC thì:
GA = |ma; GB = |mb; GC = |mc
Vậy ta có kết quả:
m2 + m2 + m2 = -|(a2 + b2 + c2)
MA2 + MB2 + MC2 = MA2 + MB2 + MC2 = (MG + GA)2 + (MG + GB)2 + (MG + GC)2 = 3MG2 + GA2 + GB2 + GC2 + 2MG(GA + GB + GC)
= 3MG2 + GA2 + GB2 + GC2
Cliú ý:
Công thức: MA2 + MB2 + MC2 = 3MG2 + GA2 + GB2 + GC2 được gọi là công thức Lepnit.
BÀI 8
Tính góc A của tam giác ABC biết các cạnh a, b, c thỏa hệ thức: b(b2 - a2) = c(c2 - a2)	(b * c)
Giải
Ta có:
b (b2 — a2) = c(c2 - a2) b3 - ơ
o
(b - c)(b2 + c2 + bc) = a2(b - c)
b2 + c2 + bc - a2 (b * c)
b2 + c2 - a2 = -be	(1)
Mà
A	b2+c2-a2
cosA -	~	(2)
2bc
Từ (1) và (2) suy ra: COS A =	= -A
Á DC	Zi
Vậy: A = 120°.
BÀI 9
Cho tam giác ABC thỏa điều kiện: ffl3 + p3-h3
'	= b2	(1)
5 a + c - b
a = 2bcosC	(2)
Chứng minh tam giác ABC đều.
Giải
(1) 
a3 + c3 - b3 = b2(a
+ c) - b3
a3 + c3 = b2(a + c)
 a2 - ac + c2
= b2
a2 + c2 - b2 = ac
a2 + c2 - b2
1
2ac
2
cosB = —
 B = 60°
Theo giả thiết ta có: a = 2b cosC Mặt khác theo định lí hàm cosin ta có:
c2 = a2 + b2 - 2ab cosC	(3)
Thay (2) vào (3) ta được:
c2 = a2 + b2 - a2 b2 = c2 b = c Vậy tam giác ABC cân có góc B = 60°, nên nó là tam giác đều.
BÀI 10
Cho P(3, 0) và hai đường thẳng	(d1): 2x - y - 2 = 0
(d2): X + y + 3 = 0
Gọi (d) là đường thẳng qua p và cắt dp d2 tại A, B sao cho PA = PB. Viết phương trình đường thẳng (d).
B e (d9) nên XB + yB + 3 =
X. + XB
Do p là trung diêm AB nên <
ỉ\	15
yA + yB
Vậy ta có hệ phương trình:
2xA -yA =2
(1)
< XB + yB = -3
(2)
XA + XB = 6
(3)
yA + yB = 0
(4)
Từ (2), (3') và (4), ta được:
(6 - XA) + (-yA) = -3
«	XA + yA = 9
Afll 16
(5)
Từ (1) và (5), ta có: A
•
Giải
Ta có:	A 6 (dj) nên 2xA - yB - 2 = 0
(1)
(2)
(3)
(4)
(d) nhận AP =	j>-^] = -f(1’8) là VTCP.
X - 3 y - 0
Vậy phương trình (d) là: ——— = ——-.
BÀI 11
Lập phương trình các cạnh của AABC biết B(-4; -5) và hai đường cao hạ từ hai đỉnh còn lại có phương trình: 5x + 3y - 4 = 0 và 3x + 8y + 13 = 0.
Giải
Gọi (AH): 5x + 3y - 4 = 0 và (CH): 3x + 8y + 13 = 0
(BC) qua B và vuông góc (AH) nên có PVT n = (3, -5) Phương trình (BC) là:
3(x + 4) - 5(y + 5) = 0 3x - 5y - 13 = 0
(AB) qua B và vuông góc (CH) nên có PVT n' = (8, -3) Phương trình (BA) là:
8(x + 4) - 3(y + 5) = 0 « 8x - 3y + 17 = 0
Tọa độ A là nghiệm cúa hệ phương trình:
Vậy A(-l, 3)
J8x-3y = -17 (5x + 3y = 4
Tọa độ c là nghiệm của hệ phương trình:
Í3x - 5y = 13
(3x + 8y = -13 Vậy C( 1,-2)
(AC) qua A và có VTCP AC = (2, -5)
, x + 1 y - 3
Phương trình chính tắc (AC):	— =
2	—5
BÀI 12
Cho đường tròn (C): X2 + y2 + 2x - 4y - 20 = 0 và A(3, 0).
Viết phương trình đường thẳng chứa dây cung của đường tròn qua A khi:
Dây cung có độ dài lớn nhất.
Dây cung có độ dài nhỏ nhất.
Giải
(C) có tâm I(-l, 2), bán kính R = 71 + 4 + 20 = 5
Ta có: rpjyQ = 9+ 6-20A nằm trong đường tròn (C).
Dây cung dài nhất đó là đường kính.
Phương trình đường thẳng AI là:
x - 3 y - 0
x + 2y-3 = 0
Ta có: Ô(I, d) = IH < IA = 720
Độ dài dây cung nhỏ nhất IH dài nhất H = A.
Vậy dây cung ngắn nhất qua A là dây ± AI tại A, lúc đó AI = (-4, 2) là
VTPT. Vậy phương trình (d):
-4(x - 3) + 2(y - 0) - 0	2x-y-6 = 0
BÀI 13
Cho đường tròn (C) có phương trình: X2 + y2 + 4x + 4y - 17 = 0. Viết phương trình tiếp tuyến A với (C) trong mỗi trường hợp sau:
A tiếp xúc với (C) tại M(2; 1).
A vuông góc với đường thẳng (D): 3x - 4y + 1 - 0.
A đi qua A(2; 6).
Giải
A: 4x + 3y - 11 - 0.
Có hai tiếp tuyến: Ap
Có hai tiếp tuyến:
4x + 3y + 39 = 0; A2: 4x + 3y -11 -32 + 5755
A,: y =
-(x-2) + 6
0.
_ -32-5755	c
y =	(.X - 2) + 6
BÀI 14
Lập phương trình chính tắc của elip (E) biết:
A(0; -2) là một đỉnh và F(l; 0) là nột tiêu điểm của (E);
F1(-7; 0) là tiêu điểm và (E) đi qua M (-2; 12).
Giải
Elip (E) có phương trình chính tắc: —7 + 7-7 = 1 (a > b > 0).
a b
A(0; -2) là một đỉnh => b = 2; F(l; 0) là một tiêu điểm => c = 1.
a2 = b2 + c2 = 5. Phương trình của (E) là: — +	= 1.
5	4
Fx(-7; 0) là một tiêu điểm => tiêu điểm thứ hai là: F2(7; 0).
M e (E) => 2a = MFX + MF2 = 7(-7 + 2)2 + 12" + 7(7 + 2)2 + 122 = 28 =>a = 14
F(-7; 0) là tiêu điểm => c = 7 => b2 = a2 - c2 = 196 - 49 = 147
Phương trình của (E) là: -7— +	- 1.
196	147
BÀI 15
Cho elip (E) có phương trình 7- +	= 1
9	4
Tìm tọa độ các tiêu điểm, các đỉnh, tính tâm sai và vẽ (E).
Xác định m để đường thẳng (D): y = X + m và (E) có điểm chung.
Giải
a) a2 = 9 => a = 3 b2 = 4 b = 2 c2 = a2 - b2 = 5 => c = 75 -
Các tiêu điểm: Fx(~75 ; 0), F2( 75 ; 0).
Các đỉnh: (±3; 0), (0; ±2).
Tamsai:e=~.
3
b) Hoành độ giao điểm của (D) và (E) là nghiệm phương trình:
1 13x2 + 18mx + 9m2 - 36 = 0	(1)
X2 (x + m)2
—	1	
9	4
(D) và (E) có điểm chung (1) có nghiệm A’ > 0 81m2 - 13(9m2 - 36) > 0 m2 -7Ĩ3 < m < 7Ĩ3 •
Vậy với -7Ĩ3 < m < 7Ĩ3 thì (D) và (E) có điểm chung.
BÀI 16
Tìm phương trình chính tắc (hoặc thường gặp) của elip (E) biết:
(E) qua hai điểm	N
f375 475	„
M ■	, V nằm trên (E) vìMn
5	5
-2,-
'	575A nằm trên (E) vì M nhìn hai tiêu điểm dưới một
góc vuông và hai tiêu điếm nằm trên Ox.
Giải
Vì tiêu điểm trên Ox nên (E) có dạng:
„2 2
X y
—7 + 7-7 = 1 (với a > b) a b
375 475
9 . 16	,
e (E) nên được: 7—7 + 777 = 1 03	0 D
(1)
V.	7
M nhìn Fp F2 dưới một góc vuông nên M thuộc đường tròn:
,	__9	.9	. 9	16	2
X2 + y2 = c2 => 7 + — = c
5	5
=> c2 = 5 => a2 - b2 = 5
Từ (1) và (2) được hệ:
a2 - b2 = 5 9	16
5a2	5b2
a2 = b2 + 5
9	16
5(b2 + 5) + 5b2
(2)
(3)
(3) cho: 9b2 + 16(b2 + 5) = 5b2(b2 + 5) 80
 5b4 = 80 b4 = -7- = 16 b2 = 4 a2 = 9 5