Giải Toán 12: Bài 1. Hệ tọa độ trong không gian

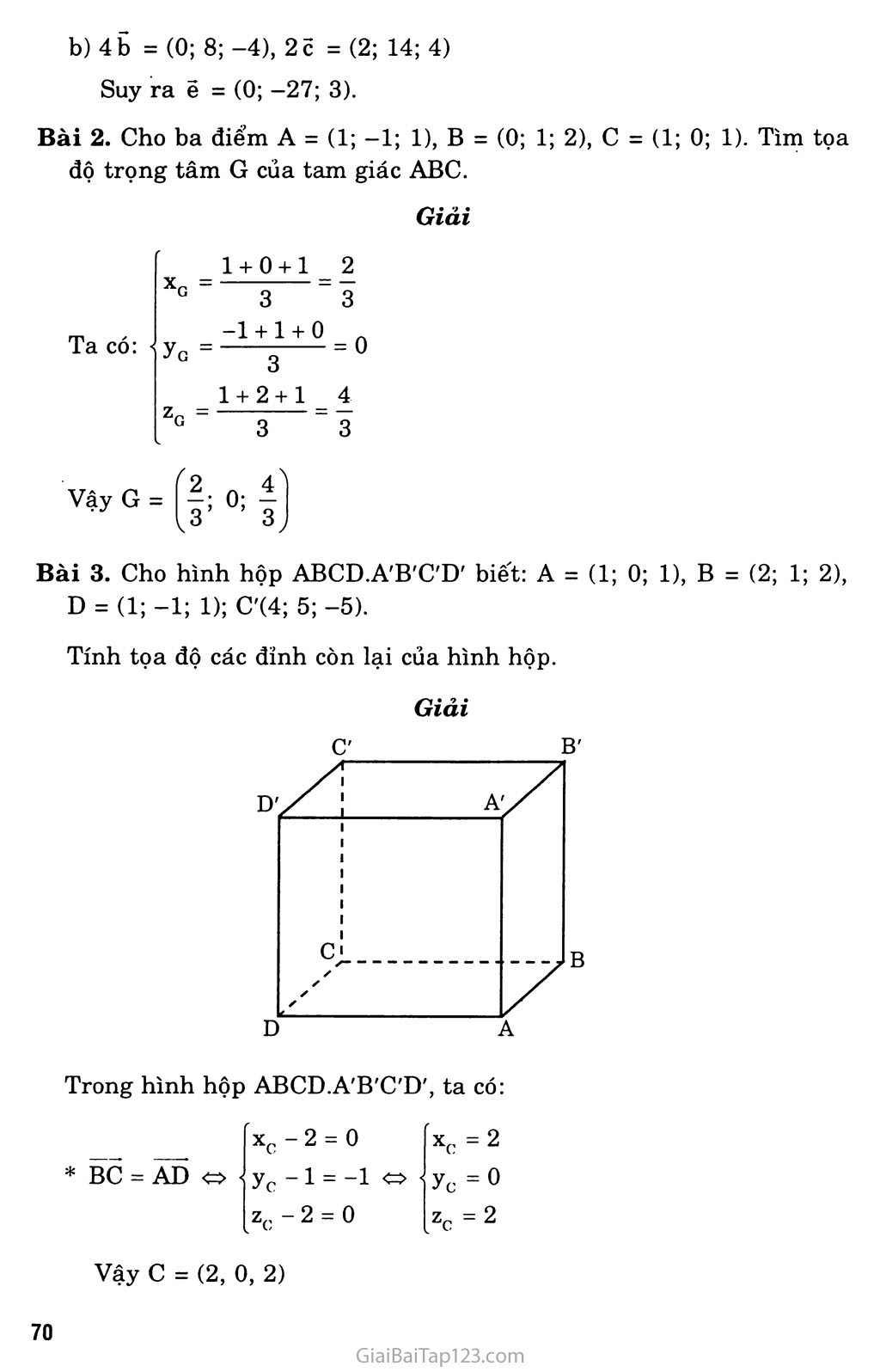
Chương III
PHƯƠNG PHÁP TỌd ĐỘ
TRONG KHÔNG GIRN
§1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A. KIẾN THỨC CẦN NHỚ
Hệ tọa độ trong không gian
Hệ tọa độ trong không gian là hệ gồm ba trục x'Ox, y'Oy, z'Oz vuông góc với nhau từng đôi một. Trên mỗi trục nói trên lần lượt có các vectơ đơn vị i, j, k .
Kí hiệu: Oxyz hay (O: I, J, k)
Điểm o được gọi là gốc tọa độ.
Các trục x'Ox, y'Oy, z'Oz lần lượt gọi là trục hoành, trục tung và trục cao.
Các mặt phẳng (Oxy), (Oyz), (Ozx) gọi là các mặt phẳng tọa độ.
Tọa độ của một điểm
Trong không gian tọa độ Oxyz, với mỗi điểm M tồn tại bộ ba số (x; y; z) duy nhất sao cho OM = XI + yj + zk
x: gọi là hoành độ của điểm M
y: gọi là tung độ của điểm M
z: gọi là cao độ của điểm M
Bộ ba số (x; y; z) được gọi là tọa độ củá điểm M.
Kí hiệu M(x; y; z) hay M = (x; y; z).
Vậy: M(x; y; z) OM = xĩ + yj + zk
II. Tọa độ của một vectơ
Trong không gian tọa độ Oxyz, cho một vecto' ũ. Khi đó tồn tại bộ ba số (x; y; z) duy nhất sao cho ũ = xi + yj + zk Bộ ba số (x; y z) hay ũ = (x; y; z)
Vậy ũ (x; y; z) ũ = xi + yj + zk
Suy ra: ĩ = (1; 0; 0), J = (0; 1; 0), k = (0; 0; 1).
Biểu thức tọa độ của các phép toán vectơ
Cho các vecto’ ũ = (Xi; yi; Zi), V = (x2, y2, z2) và số k tuỳ ý, ta có:
ũ = õ « Xi = 0, yi = 0, Zi = 0
ũ = V Xi = x2, yi = y2, Zi = z2.
• ũ + V = (xi + x2; y! + y2; Zi + z2)
ũ - V = (Xi - x2; yi - y2; Zi - z2)
kũ = (kxi; kyi; kzx)
ũ. V = Xjx2 + yiy2 + ZiZ2
|ũ| = ựxf+ỹf7zf
cos(ũ,v) =
7x-; + yf+z^xỉ + yỉ + z“
Ũ 1 V ũ. V = 0 XiX2 + yiy2 + ZiZ2 = 0
Cho A(xa; yA; ZA) và B(xb; yB; ZB). Ta có:
AB = (xB - xa; yB - yA; ZB - ZA)
AB = ự(xB - XA)2 + (yB - yA)2 + (zB- ZA)2
Chia một đoạn thẳng theo một tỉ số cho trước
Nếu MA = kMB (k * 1) ta nói M là điểm chia đoạn thẳng AB theo tỉ số k.
Với A(xa; yA; ZA) và B(xb; yB; ZB). Ta có:
MA = kMB (k * 1) •
XA - kxB
1-k yA - kyB 1-k
ZA - kzB
l-k
Với k = -1 ta được tọa độ trung điểm I của đoạn thẳng AB là:
<XA+XB. yA+yB; za+zb"
; 2 ’ 2 ’ 2 ,
Phương trình của một mặt cầu
Trong không gian tọa độ Oxyz, phương trình của mặt cầu (S) tâm I (a; b; c) bán kính R có dạng:
(x - a)2 + (y - b)2 + (z - c)2 = R2
Trường hợp đặc biệt: Phương trình mặt cầu có tâm là gốc tọa độ o bán kính R là:
__2	. __2 .	_2	r>2
X + y + z = R
Trong không gian tọa độ Oxyz, phương trình:
X2 + y2 + z2 + 2ax + by + 2xz + d = 0 với điều kiện a2 + b2 + c2 - d > 0 là phương trình của mặt cầu tâm I(—a; —b; —c) bán kính R = Va2 + b2 + c2 — d .
B. BÀI TẬP
Các bài tập sau đây đều xét trong kliông gian Oxyz.
Bài 1. Cho ba vectơ ã = (2; -5; 3), b = (0; 2; -1), C = (1; 7; 2).
Tính tọa độ của vectơ d = 4ã - Ậb + 3c.
■	3
Tính tọa độ của vectơ ẽ = ã - 4b - 2c.
Giải
0; -I
3	3
, 3c = (3; 21; 6)
Suy ra d =
t 1	55a
11; ị; 42 3	3
4ã = (8; -20; 12), jb = 3
4b = (0; 8; -4), 2 c = (2; 14; 4)
Suy ra ẽ = (0; —27; 3).
Bài 2. Cho ba điểm A = (1; -1; 1), B = (0; 1; 2), c = (1; 0; 1). Tìm tọa độ trọng tâm G của tam giác ABC.
Giải
Ta có:
1+0+12 ” 3
G 3
-1 + 1 + 0 yG = -
G 3
1+2+14 3	- 3
ZG =
Vậy G =
<2	_ 4^
I; °; I
,3’ 3y
Bài 3. Cho hình hộp ABCD.A'B'C'D' biết: A = (1; 0; 1), B = (2; 1; 2), D = (1; -1; 1); C'(4; 5; -5).
Tính tọa độ các đỉnh còn lại của hình hộp.
Giải
Trong hình hộp ABCD.A'B'C'D', ta có:
xc-2 = 0 • yc -1 = -1 
zc - 2 = 0
xc = 2 •yc = 0 zc = 2
Vậy c = (2, 0, 2)
AA' = CỜ •
XA, =3 yA' = 5
XA. - 1 = 2 yA. - 0 = 5 o < ZA, -1 = -7
A
Vậy A' = (3; 5; -6)
BB' = CC' «
XB. =4
yB- = 6
ZB. = -5
XD, = 3
yD' = 4
ZD. = -6
x,-2 = 2 yB.-l = 5 o zb.-2 = -7
XD. -1 = 2
* DÌ)' = CC' <
B' = (4; 6; -5)
yu. + 1 = 5 » z0.-l = -7
=> D' = (3; 4; -6)
Bài 4. Tính
ã.b với ã = (3, 0, 2), b = (2, -4, 0)
c . d với C = (1, -5, 2), d = (0, 3, -3).
Giải
ã.b = 3.2 + O.(-4) + 2.0 = 6
c.d = 1.0 + (-5).3 + 2(-3) = -21
Bài 5. Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:
X2 + y2 + z2 - 8x - 2y + 1 = 0.
3x2 + 3y2 + 3z2 - 6x + 8y + 15z -3 = 0
Giải
X2 + y2 - 8x - 2y + 1 = 0 (x - 4)2 + (y - l)2 + z2 = 16 Vậy mặt cầu có tâm 1(4; 1; 0), bán kính R = 4.
3x2 + 3y2 + 3z2 - 6x + 8y + 15z -3 = 0
 X2 + y2 + z2 - 2x + -|- y + 5z - 1 = 0 3
 (x - l)2 +
+
361
36
Vậy mặt cầu có tâm I
, bán kính R =
6
k °	)
Bài 6. Lập phương trình mặt cầu trong hai trường hợp sau đây:
Có đường kính AB với A(4; -3; 7), B(2; 1; 3)
Đi qua điểm A(5; -2; 1) và có tâm C(3; -3; 1).
Giải
Mặt cầu (S) đường kính AB có tâm là trung điểm I của đoạn
thẳng AB và bán kính R =	.
2
+ A(4; -3; 7), B(2; 1; 3) => 1(3; -1; 5).
+ R = |ự(-2)2 +42 + (-4)2 = 3 2
Vậy phương trình của mặt cầu là: (x - 3)2 + (y + l)2 + (z - 5)2 = 9
Mặt cầu có tâm C(3; -3; 1) và đi qua điểm A(5; -2; 1) có bán kính là:
R = CA = V22 + l2 + o2 = Võ Vậy phương trình của mặt cầu là:
(X - 3)2 + (y + 3)2 + (z - l)2 = 5