Giải Toán 12: Bài 1. Khái niệm về mặt tròn xoay

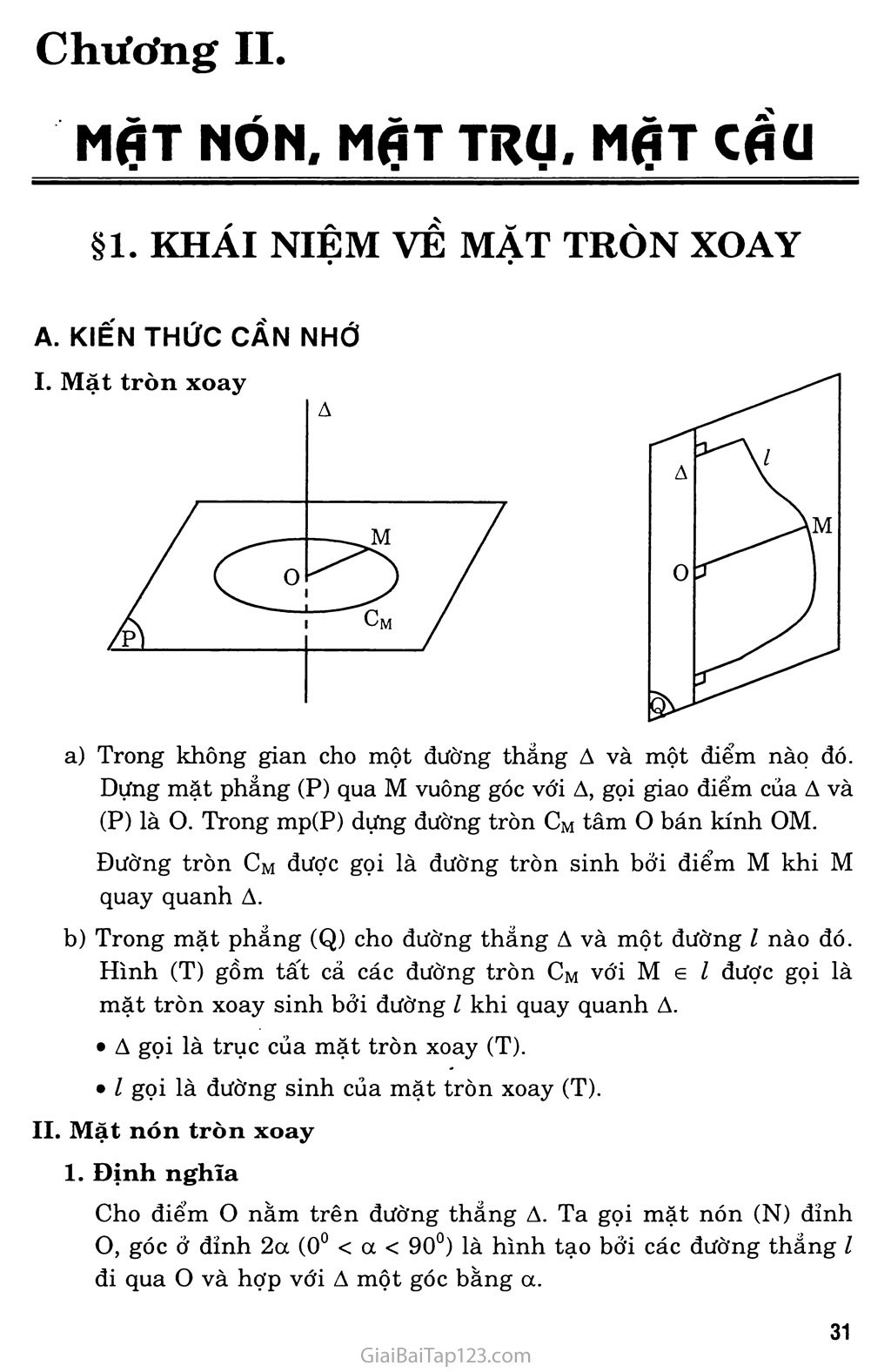
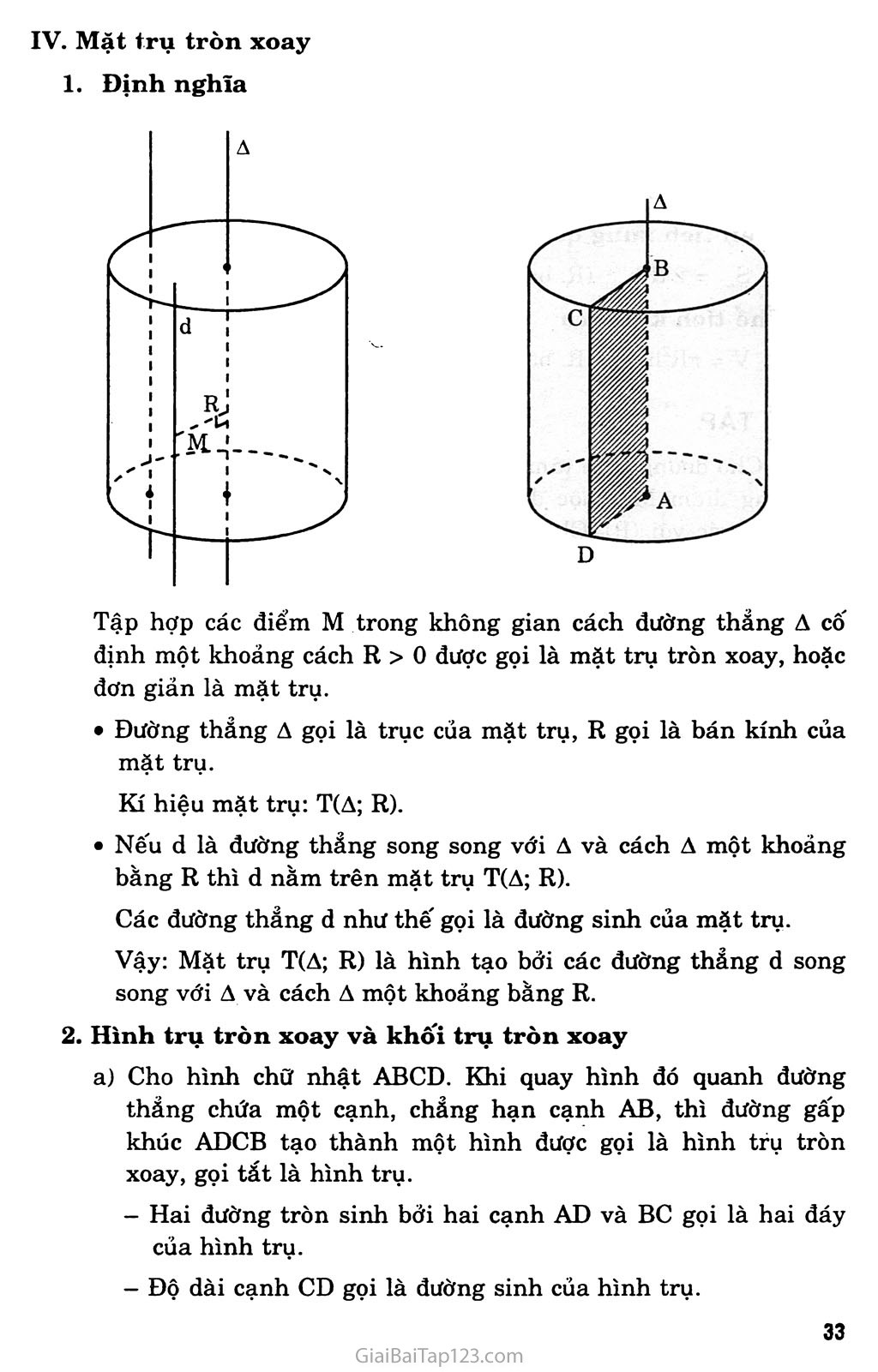
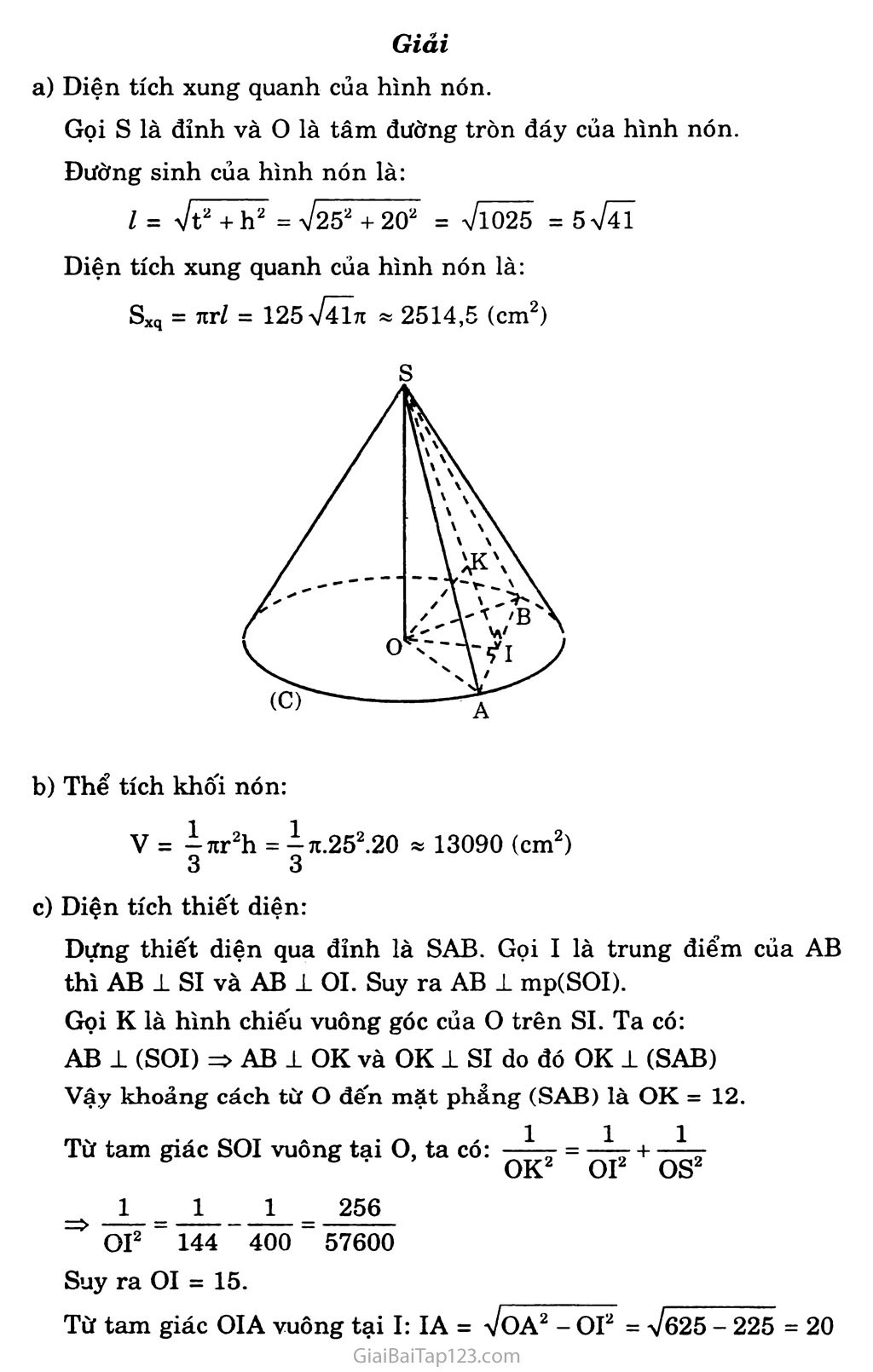
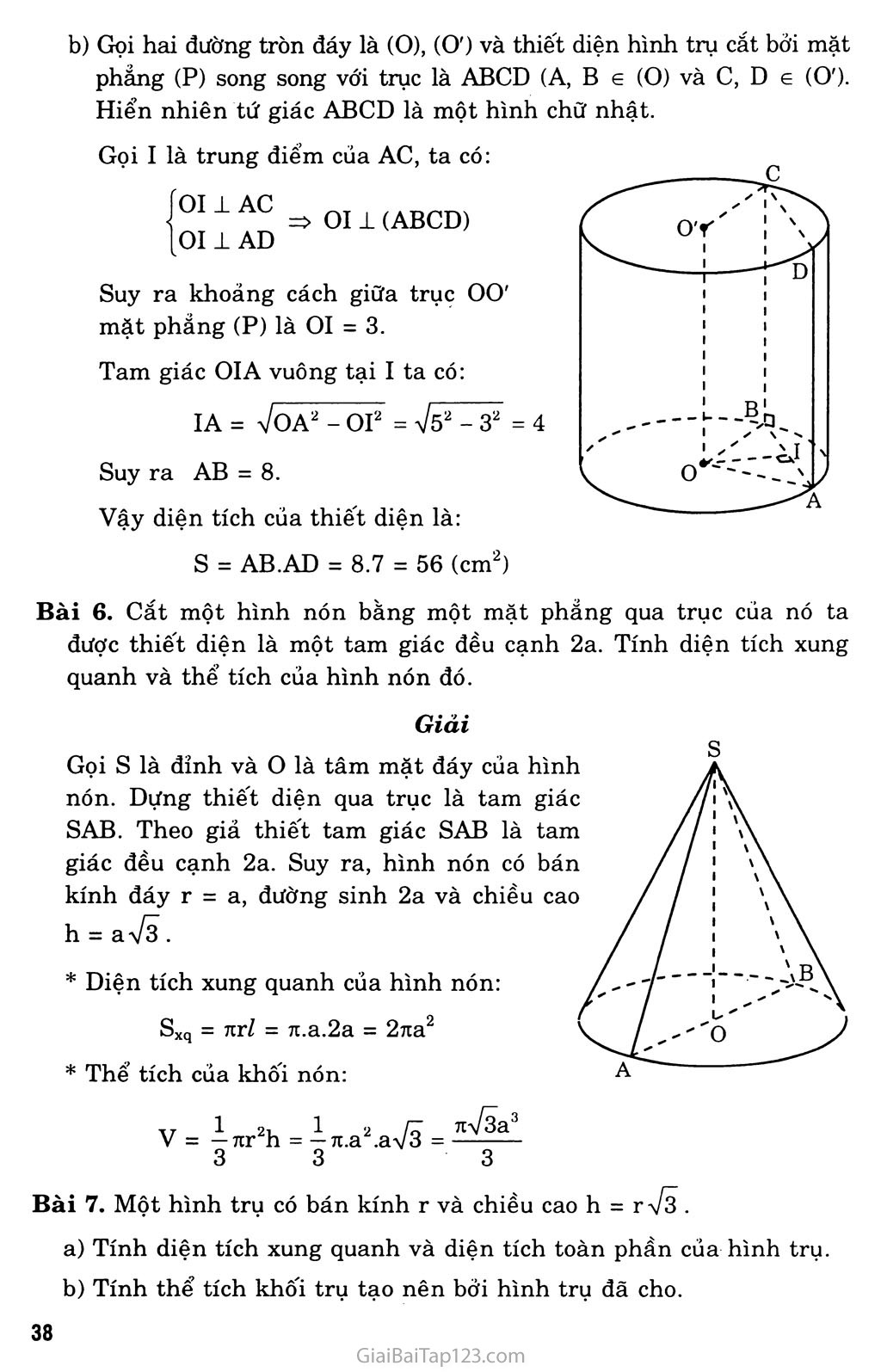
Chương II.
MỘT NÓN, MỘT TRỌ, MỘT cầu
§1. KHÁI NIỆM VỀ MẶT TRÒN XOAY
A. KIẾN THỨC CẦN NHỚ
Trong không gian cho một đường thẳng A và một điểm nàọ đó. Dựng mặt phẳng (P) qua M vuông góc với A, gọi giao điểm của A và (P) là o. Trong mp(P) dựng đường tròn CM tâm o bán kính OM.
Đường tròn Cm được gọi là đường tròn sinh bởi điểm M khi M quay quanh A.
Trong mặt phẳng (Q) cho đường thẳng A và một đường l nào đó. Hình (T) gồm tất cả các đường tròn Cm với M 6 l được gọi là mặt tròn xoay sinh bởi đường l khi quay quanh A.
A gọi là trục của mặt tròn xoay (T).
l gọi là đường sinh của mặt tròn xoay (T).
Mặt nón tròn xoay
Định nghĩa
Cho điểm o nằm trên đường thẳng A. Ta gọi mặt nón (N) đỉnh o, góc ở đỉnh 2a (0° < a < 90°) là hình tạo bởi các đường thẳng l đi qua o và hợp với A một góc bằng oc.
Đường thẳng A gọi là trục của mặt tròn.
Các đường thẳng l gọi là đường sinh của mặt nón.
Tính chất
Cắt mặt nón (N) bằng mặt phẳng (P) vuông góc với trục A và không qua o, ta được giao tuyến là một đường tròn có tâm trên A.
Cắt mặt (N) bằng mặt phẳng (P) qua trục A, ta được giao tuyến là đường sinh đôĩ xứng với nhau qua A.
Hình nón tròn xoay và khối nón tròn xoay Q
Hình nón tròn xoay
Cho tam giác OIA vuông tại I_ Khi quay tam giác đó quanh cạnh góc vuông OI thì đường gấp khúc OAI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.
Điếm o gọi là đỉnh của hình nón.
Đoạn thẳng OI gọi là trục của hình nón, độ dài OI gọi là chiều cao của hình nón.
Hình tròn (C) sinh bởi cạnh IA gọi là đáy của hình nón. Trên đường tròn (C) lấy điểm M bất kì, đoạn thẳng OM gọi là đường sinh của hình nón. Tất cả các đường sinh đều bằng nhau.
Nếu cắt hình nón bằng một mặt phẳng qua hai đường sinh, ta được thiết diện là một tam giác cân.
Nếu cắt hình nón bằng một mặt phẳng vuông góc với trục 10 (không qua O) ta được giao tuyến là một đường tròn có tâm nằm trên 01.
Khôi nón tròn xoay
Hình nón cùng với phần bên trong của nó được gọi là khôi nón xác định bởi hình nón đó.
Diện tích xung quanh của hình nón
Sxq = tiRZ (R: là bán kính đáy, /: độ dài đường sinh)
Thể tích khôi nón
(R: bán kính đáy, h: chiều cao)
V = ịnR2h
3
IV. Mặt trụ tròn xoay 1. Định nghĩa
B
X
✓
Tập hợp các điểm M trong không gian cách đường thẳng A cố định một khoảng cách R > 0 được gọi là mặt trụ tròn xoay, hoặc đơn giản là mặt trụ.
Đường thẳng A gọi là trục của mặt trụ, R gọi là bán kính của mặt trụ.
Kí hiệu mặt trụ: T(A; R).
Nếu d là đường thẳng song song với A và cách A một khoảng bằng R thì d nằm trên mặt trụ T(A; R).
Các đường thẳng d như thế gọi là đường sinh của mặt trụ.
Vậy: Mặt trụ T(A; R) là hình tạo bởi các đường thảng d song song với A và cách A một khoảng bằng R.
Hình trụ tròn xoay và khối trụ tròn xoay
Cho hình chữ nhật ABCD. Khi quay hình đó quanh đường thẳng chứa một cạnh, chẳng hạn cạnh AB, thì đường gấp khúc ADCB tạo thành một hình được gọi là hình trụ tròn xoay, gọi tắt là hình trụ.
Hai đường tròn sinh bởi hai cạnh AD và BC gọi là hai đáy của hình trụ.
Độ dài cạnh CD gọi là đường sinh của hình trụ.
Mặt sinh bởi cạnh CD gọi là mặt xung quanh của hình trụ.
Khoảng cách giữa hai mặt chứa hai đáy gọi là chiều cao của hình trụ.
Phần không gian được giới hạn bởi một hình trụ tròn xoay kế’ cả hình trụ đó được gọi là khối trụ tròn xoay.
Diện tích xung quanh của hình trụ
SXq = 2ĩụRh (R: bán kính đáy, h: chiều cao)
Thể tích khôi trụ
V = 7iR2h (R: bán kính đáy, h: chiều cao)
B. BÀI TẬP
Bài 1. Cho đường tròn tâm o bán kính r nằm trên mặt phẳng (P). Từ những điểm M thuộc đường tròn này ta kẻ những đường thẳng vuông góc với (P). Chứng minh rằng những đường thẳng như vậy nằm trên một mặt trụ tròn xoay. Hãy xác định trục và bán kính của mặt trụ đó.
Gọi đường tròn tâm o bán kính r nằm trong mặt phẳng (P) là (C). Dựng đường thẳng a qua M vuông góc với (P), và đường thẳng A vuông góc với (P) tại o. Nôi đoạn thẳng OM. Ta có ai mp(P) nên a 1 OM và OM = r vì M nằm trên đường tròn (C), r chính là khoảng cách giữa a và A.
Suy ra a là đường thẳng thay đổi luôn song song với đường thẳng có đỉnh A và cách A một khoảng không đổi bằng r.
Vậy đường thẳng a luôn nằm trên mặt trụ tròn xoay, trục A, bán kính r.
Bài 2. Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khôi tròn xoay sinh ra bởi:
Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.
Ba cạnh của một tam giác cân khi quay quanh trục đối xứng của nó.
Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông.
Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh.
Giải
Gọi hình chữ nhật ABCD với AB = a, AD = b. Giả sử ta cho ba cạnh AB, BC, CD quay xung quanh đường thẳng AD, khi đó hình tròn xoay sinh ra là hình trụ tròn xoay có bán kính đáy R = a và chiều cao h = b.
Xét tam giác ABC cân tại A, kẻ đường cao AH. Khi chơ các cạnh của tam giác này quay xung quanh đường thẳng AH, ta được
BC
. hình tròn xoay sinh ra là hình nón có bán kính đáy R = và có trục là đoạn thẳng AH.
Xét miền tam giác vuông ABC vuông tại A. Khi cho miền tam giác này quay xung quanh đường thẳng AB, ta được một khối nón tròn xoay có bán kính đáy R = AC và chiều cao h = AB. Tương tự nếu cho miền tam giác này quay xung quanh đường thẳng AC, ta được một khối nón tròn xoay có bán kính đáy R = AB và chiều cao h = AC.
Xét miền hình chữ nhật là ABCD với AB = a, AD = b. Giả sử ta cho miền hình chữ nhật này quay xung quanh đường thẳng AD thì ta được một khối trụ tròn xoay có bán kính đáy R = a và chiều cao h = b.
Bài 3. Cho hình tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.
Tính diện tích xung quanh của hình nón đã cho.
Thể tích của khôi nón được tạo thành bởi hình nón đó.
Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.
Giải
a) Diện tích xung quanh của hình nón.
Gọi s là đỉnh và o là tâm đường tròn đáy của hình nón. Đường sinh của hình nón là:
l = 7t2 + h2 = V252 + 202 = 7l025 = 5 7ĨĨ Diện tích xung quanh của hình nón là:
Sxq = Ttr/ = 125 74171 « 2514,5 (cm2)
Thể tích khối nón:
V = ịĩtr2h = ịĩt.252.20 « 13090 (cm2)
3	3
Diện tích thiết diện:
Dựng thiết diện qua đỉnh là SAB. Gọi I là trung điểm của AB thì AB ± SI và AB _L OI. Suy ra AB ± mp(SOI).
Gọi K là hình chiếu vuông góc của o trên SI. Ta có:
AB 1 (SOI) => AB 1 OK và OK 1 SI do đó OK 1 (SAB)
Vậy khoảng cách từ o đến mặt phẳng (SAB) là OK = 12.
Từ tam giác SOI vuông tại o, ta có: 777-7 = —77 + 7777 OK2 OI2 OS2
1 _ _Ị	1_ _ 256
OI2 - 144	400 “ 57600
Suy ra OI = 15.
Từ tam giác OIA vuông tại I: IA = 7oA2 - OI2 = 7625 - 225 = 20
Ta có: SI.OK = OS.OI => SI =	= 25
OK 12
Diện tích của thiết diện:
stđ = I AB.SI = IA.SI = 20.25 = 500 (cm2)
2
Bài 4. Trong không gian cho hai điểm A, B cố định và có độ dài AB = 20 cm. Gọi d là một đường thẳng thay đổi luôn luôn đi qua A và cách B một khoảng cách bằng 10 cm. Chứng tỏ rằng đường thắng d luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.
Giải
Gọi A là đường thẳng qua A, B và H là hình chiếu vuông góc của B trên d, theo giả thiết BH = 10. Đặt a = (A,d).
Từ tam giác AHB vuông tại H:
BH 10	1
AB 20	2
=> a = 30°
Như thế là đường thẳng đi qua điếm A và hợp với đường thẳng A cố định một góc a = 30°.
Vậy tập hợp các đường thẳng d là mặt nón đỉnh A, trục A, gốc đỉnh 2a = 60°.
Bài 5. Một hình trụ có bán kính đáy r = 5 cm và có khoảng cách giữa hai đáy bằng 7 cm.
Tính diện tích xung quanh của hình trụ và thể tích của khôi trụ được tạo nên.
Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3 cm. Hãy tính diện tích của thiết diện được tạo nên.
Giải
a) * Diện xích xung quanh của hình trụ:
sxq = 2xrh = 2rt.5.7 = 70n a 220 (cm2)
* Thể tích nr2h = x.25.7 = 175n a 549,78 (cm3)
b) Gọi hai đường tròn đáy là (O), (O') và thiết diện hình trụ cắt bởi mặt phẳng (P) song song với trục là ABCD (A, B G (O) và c, D G (O'). Hiển nhiên tứ giác ABCD là một hình chữ nhật.
Gọi I là trung điểm của AC, ta có:
. Ỷ AC => OI 1 (ABCD)
[011 AD
Suy ra khoảng cách giữa trục 00' mặt phẳng (P) là 01 = 3.
Tam giác OIA vuông tại I ta có:
IA = VoA2 - OI2 = Võ2 - 32 Suy ra AB - 8.
Vậy diện tích của thiết diện là:
s = AB.AD = 8.7 = 56 (cm2)
Bài 6. Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh và thể tích của hình nón đó.
Giải
Gọi s là đỉnh và o là tâm mặt đáy của hình nón. Dựng thiết diện qua trục là tam giác SAB. Theo giả thiết tam giác SAB là tam giác đều cạnh 2a. Suy ra, hình nón có bán kính đáy r = a, đường sinh 2a và chiều cao h = a Vã.
Diện tích xung quanh của hình nón:
Sxq = 7irZ = 7i.a.2a = 27ia2
Bài 7. Một hình trụ có bán kính r và chiều cao h = r V3 .
Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 30°. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.
Giải
a) * Diện tích xung quanh của hình trụ:
Sxq = 2nrh = 2nrrV3 = 2ĩt V3 r2
* Diện tích toàn phần của hình trụ:
Thê’ tích khôi trụ:
V = 7ir2h = 7ir2.r V3 = V3 7ir3
Khoảng cách giữa đường thẳng AB và trục hình trụ:
Gọi (O) là đường tròn đáy chứa điểm A và (O') là đường tròn đáy chứa điếm B.
Kẻ đường sinh BC, suy ra oc // OB và BC // 00'.
Từ giả thiết suy ra ABC = 30°.
Gọi I là trung điểm của AC thì 011 AC, ngoài ra ta cũng có 011 BC. Do đó 01 1 mp(ABC).
Vì 00' // BC nên 00' // mp(ABC).
Suy ra 01 là khoảng cách giữa 00' và AB.
Từ tam giác ABC vuông tại c ta có AC = BCtan30° = r.
... rựã
Vậy khoảng cách giữa trục hình trụ và đường thẳng AB là
z
Bài 8. Một hình trụ có hai đáy là hai hình tròn (0; r) và (O'; r). Khoảng cách giữa hai đáy là 00' = rVã. Một hình nón có đỉnh là O' và có đáy là hình tròn (O; r).
a) Gọi Si là diện tích xung quanh của hình trụ và S2 là diện tích g
xung quanh của hình nón, hãy tính tỉ số —
Từ tam giác OAI vuông tại I ta có:
S2
b) Mặt xung quanh của hình nón chia khôi trụ thành hai phần, hãy tính tỉ số thể tích hai phần đó.
Giải
a) * Diện tích xung quanh của hình trụ:
Si = 2rcrh = 2 V3 7tr2 * Diện tích xung quanh của hình nón:
s2 = nrl
Trong đó: z = ựr2 + (rV3)2 = 2r Do đó:	s2 = 7tr.2r = 2nr2
o.... — ■	_ 2V3jtr2 /T
Suyra:
b) Gọi Vi là thể tích của khối nón và v2 là thể tích của phần còn lại.
Vj = ịxr2.r V3 - -ệnr3
3	3
Thể tích khôi trụ: V = nr2.r V3 = V3 7ir3.
Suy ra: v2 = V - Vj = Vi xr3 = ^Ttr3
Vậy:
yL = i v2 2
Bài 9. Cắt hình nón đỉnh s bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng aự2 .
Tính diện tích xung quanh, diện tích đáy và thể tích của khôi nón tương ứng.
Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phảng chứa đáy hình nón góc 60°. Tính diện tích tam giác SBC.
Giải
a) * Gọi s là đỉnh và o là tâm đường tròn đáy của hình nón.
Dựng thiết diện qua trục là tam giác SAB, theo giả thiết ASAB vuông cân tại s và AB = aVã.
b) Diện tích tam giác SBC.
Dựng thiết diện qua đỉnh s thỏa mãn đề bài là SBC. Gọi I là trung điểm của BC thì OI ± BC và SI ± BC.
Suy ra sĩồ = 60°.
Từ tam giác SOI vuông tại o cho:
OI = SOcot60° = ^ệ-.ệ = ^ệ- 2	3	6
Từ tam giác OBI vuông tại I, ta có:
1^2
IB = VoB2 - OI2 =
/ cV (	/—\2	/7
av6	_ ay 3
Từ tam giác SBI vuông tại I, ta có:
SI = VSB2 - IB2 = Ja2-^ =
V 9	3
Diện tích thiết diện SBC: s = ỈBC.SI =
Bài 10. Cho hình trụ có bán kính r và có chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB và CEt lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phắng chứa hình vuông và mặt phẳng đáy.
Giải
* Tính diện tích hình vuông:
Gọi hai đường tròn đáy của hình trụ là (O), (O').
Theo giả thiết ta có A, B e (O) và c, D e (O').
Đặt AB = BC = a.
Kẻ hai đường sinh CE và DF thì dễ thấy tứ giác ABEF là hình chữ nhật; trong các tam giác vuông ABE và BEC ta có:
* Gọi a là góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.
Qua lí luận trên, ta thấy hình chữ nhật ABEF là hình chiếu vuông góc của hình vuông ABCD trên mặt phẳng đáy.
Ta có BE2 = AE2 - AB2 = (2r)2 -
5r2	3r2
Suy ra BE =
Diện tích hình chữ nhật ABEF:
rVĨÕ rựẽ _ r2Vl5
Si = AB.BE = Như vậy:
2 2
r2VĨ5
cosa = —ỳ- =
5r2