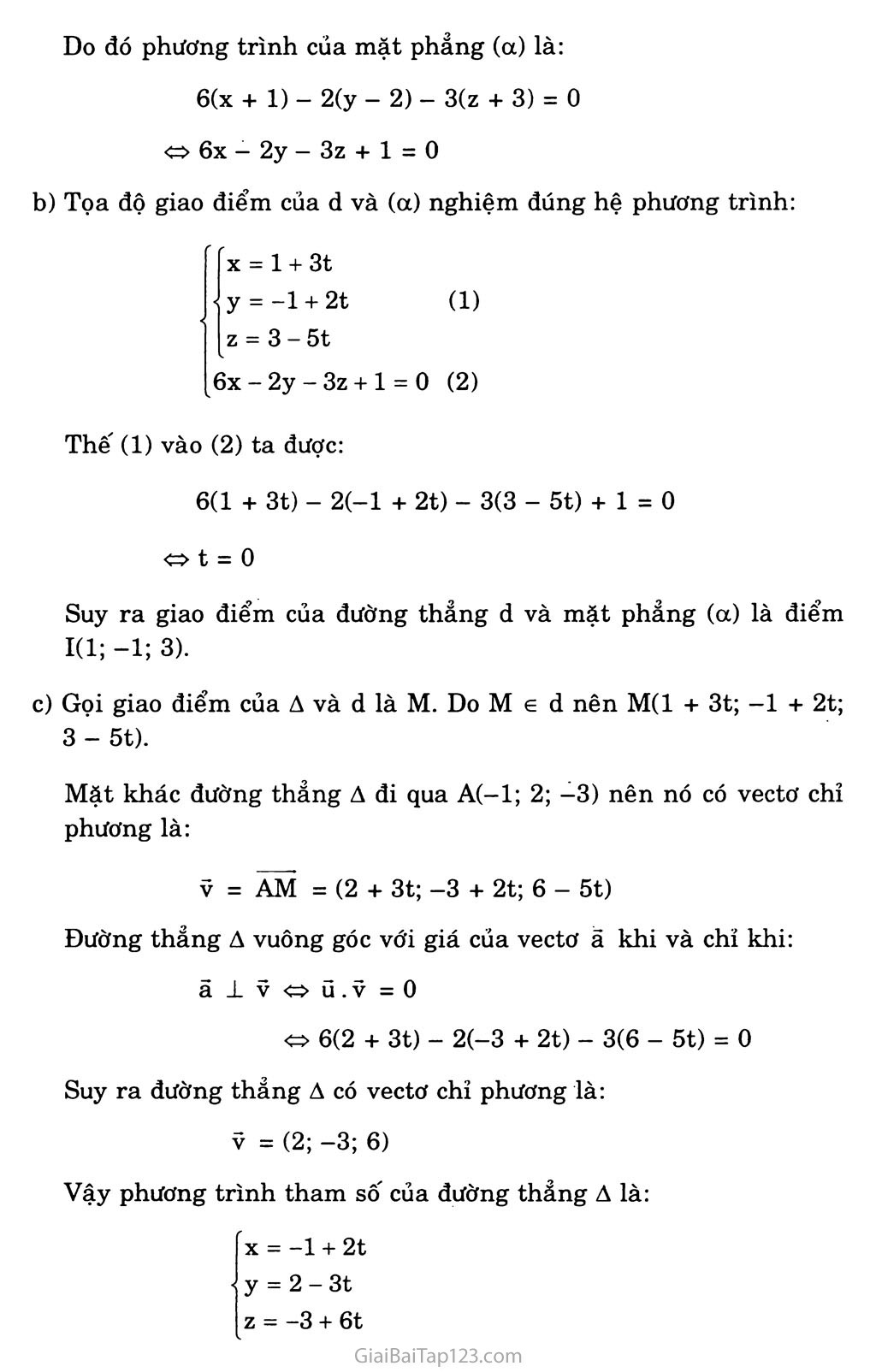Giải Toán 12: Ôn tập chương III

ÔN TẬP CHƯƠNG III
Các bài toán sau dây đều cho trong hệ tọa độ Oxyz.
Bài 1. Cho bốn điểm A(l; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1).
Chứng minh A, B, c, D là bốn đỉnh của một tứ diện.
Tìm góc giữa hai đường thẳng AB và CD.
Tính độ dài đường cao của hình chóp và A.BCD.
Giải
Để chứng minh bốn điểm A, B, c, D là bốn đỉnh của một tứ diện ta sẽ chứng minh điểm A không nằm trên mặt phẳng (BCD).
Ta có: BC = (0; -1; 1), BD = (-2; 0; -1).
Mặt phẳng (BCD) có vectơ pháp tuyến n = BC A BD = (1; -2; 2). Phương trình của mặt phẳng (BCD):
l.(x - 0) - 2(y - 1) - 2.(z - 0) = 0 x-2y-2z + 2 = 0
Ta thấy tọa độ điểm A không nghiệm đúng phương trình mật phẳng (BCD) nên A Ế mp(BCD).
Vậy A, B, c, D là bốn đỉnh của một tứ diện.
AB = (-1; 1; 0), CD = (-2; 1; -2).
Gọi (p là góc tạo bởi hai đường thẳng AB và CD.
m ,	|(-2)(-2) +1.1 + o.(-2)|	3	72
Ta có: coscp = ,	1	■ •	-	. • = r- -
7(-l)2 + l2 + o2 ạ/(-2)2 + l2 + (-2)2	V2.3	2
Suy ra <p = 45°.
Gọi h là độ dài đường cao của hình chóp A.BCD thì h là khoảng cách từ A đến mặt phẳng (BCD), do đó:
|l-2.0-2.0 + 21
h = d(A, (BCD)) =	1 = 1
Vl2 + (-2)2 + (-2)2
Bài 2. Cho mặt cầu (S) có đường kính là AB biết rằng: A(6; 2; -5),
B(-4; 0; 7)
Tìm tọa độ tâm I và tính bán kính r của mặt cầu (S).
Lập phương trình của mặt cầu (S).
Lập phương trình của mặt phẳng (ot) tiếp xúc với mặt cầu (S) tại điếm A.
Giải
Tâm I của (S) là trung điểm của AB, do đó 1(1; 1; 1).
Bán kính của (S) là:
r =	- ịự(-lO)2+ (-2)2 +.122 = 762
2 2
Mặt cầu (S) có phương trình là:
(x - l)2 + (y - l)2 + (z l)2 = 62
Mặt phẳng (a) tiếp xúc với (S) tại A nên có vectơ pháp tuyến là n = LA = (5; 1; -6).
Phương trình của (a) là:
(x - 6) + l.(y - 2) - 6(z + 5) = 0
 5x + y — 6z - 62 = 0
Bài 3. Cho bốn điểm A(-2; 6; 3), B(l; 0; 6), C(0; 2; -1), D(l; 4; 0).
Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
Tính chiều cao AH của tứ diện ABCD.
Viết phương trình mặt phẳng (a) chứa AB và song song với CD.
Giải
a) Ta có: BC = (-1; 2; -7), BD = (0; 4; -6).
Mặt phẳng (BCD) có vectơ pháp tuyến n - BC A BD = (8; —3; -2). Phương trình của mặt phẳng (BCD):
8(x - 1) - 3.(y - 0) - 2.(z - 6) = 0 8x - 3y - 2z + 4 = 0
Ta thấy tọa độ điểm A không nghiệm đúng phương trình mặt phẳng (BCD) nên A Ế mp(BCD).
Vậy A, B, c, D là bôn đỉnh của một tứ diện.
Chiều cao AH của tứ diện ABCD là khoảng cách từ A đến mặt phẳng (BCD).
Do đó:
|8 / (-2) - 3.6 - 2.3 + 4|	36
AH = 1	- 1 = ;
ự82 + (-3)2 + (~2)2	V77
Mặt phẳng (a) chứa AB và song song với CD nên điểm A(-2; 6; 3)
e (a) và có vectơ pháp tuyến là AB A CD.
Mà AB = (3; -6; 3), CD = (1; 2; 1) nên AB A CD = (-12; 0; 12) Phương trình của mặt phẳng (a):
-12(x + 2) + 12(z - 3) = 0
x-z + 5 = 0
Bài 4. Lập phương trình tham số của đường thẳng:
Đi qua hai điểm A(l; 0; -3), B(3; -1; 0).
Đi qua điểm M(2; 3; -5) và song song với đường thẳng A có
phương trình:
X = -2 + 2t y = 3-4t z = -5t
Giải
a) Gọi a là đường thẳng đi qua hai điểm A(l; 0; -3) và B(3; -1; 0) thì a có vectơ chỉ phương ũ = AB = (2; -1; 3). Do đó đường
X = 1 + 2t
thẳng a có phương trình tham số là: y = -t
z = -3 + 3t
b) Từ giả thiết suy ra A có vectơ chỉ phương V = (2; -4; -5). Gọi b là đường thẳng đi qua điểm M(2; 3; -5) và song song với A thì b nhận V làm vectơ chỉ phương.
X = 2 + 2t y = 3-4t z - -5 - 5t
Đo đó đường thẳng b có phương trình tham số là: <
Bài 5. Cho mặt cầu (S) có phương trình: (x - 3)2 + (y + 2)2 + (z - l)2 = 100 và mặt phẳng (a) có phương trình 2x - 2y - z + 9 = 0. Mặt phắng (a) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).
Giải
Từ giả thiết suy ra mặt cầu (S) có tâm 1(3; -2; 1) và có bán kính là R = 10.
Gọi d là khoảng cách từ I đến mặt phẳng (a), ta có:
,	|2.3 - 2.(-2) - 1 + 9]|
d _ J	[ _ 0
# + (-2)2 +(-l)2 Bán kính r của đường tròn (C) là:
r = Ợr2 - d2 - VlO2 - 62 = 8
Gọi J là tâm của đường tròn (C) thì J là hình chiếu vuông góc của I trên mặt phẳng (a).
Nếu gọi A là đường thẳng qua I và vuông go'c với (a) thì J là giao diêm của A và (a). Đường thẳng A có vectơ chí phương ủ là vectơ pháp tuyến của (a), ta được:
ũ = nư = (2; -2; -1)
Phương trình tham số của đường thẳng A:
X = 3 + 2t • y = -2 - 2t (*)
z = 1 - t
Tọa độ của điểm J ứng với t nghiệm đúng phương trình:
2(3 + 2t) - 2(-2 - 2t) - (1 - t) + 9 = 0
 t = -2
Thế t = -2 vào (*) ta được J(-l; 2; 3).
Bài 6. Clio mặt phẳng (a) có phương trình 3x + 5y - z - 2 = 0 và X = 12 + 4t
đường thẳng d có phương trình: -Ị y = 9 + 3t z = 1 + t
Tìm giao điểm M của đường thẳng d và mặt phẳng (a).
Viết phương trình mặt phẳng (P) chứa điểm M và vuông góc với đường thẳng d.
Giải
Mặt phẳng (a) và đường thẳng d cắt nhau, ta có:
3(12 + 4t) + 5(9 + 3t) - (1 + t) - 2 = 0 t = -3
Thế t = -3 vào phương trình của d ta được M(0; 0; -2).
Đường thẳng d có vectơ chỉ phương ũ = (4; 3; 1). Mặt phảng (p) đi qua M(0; 0; -2) và vuông góc với d nên ũ cũng là vectơ pháp tuyến của (p).
Vậy mặt phảng (p) có phương trình là:
4(x - 0) + 3(y - 0) + l.(z + 2) = 0
X = 1 + 3t
• y = -1 + 2t
z = 3 - 5t
4x + 3y + z + 2 = 0
Bài 7. Cho đường thẳng d có phương trình:
Cho điểm A(-l; 2; -3) và vectơ ã = (6; -2; —3).
Viết phương trình mặt phẳng (a) chứa điểm A và vuông góc với giá của ã.
Tìm giao điểm của d và (a).
Viết phương trình đường thẳng -A đi qua điểm A, vuông góc với giá của ã và cắt đường thẳng d.
Giải
a) Mặt phẳng (a) đi qua điểm A(-l; 2; -3) và vuông góc với giá của vectơ ã = (6; —2; -3) nên nhận ã làm vectơ pháp tuyến.
Do đó phương trình của mặt phẳng (a) là:
6(x + 1) - 2(y - 2) - 3(z + 3) = 0
 6x - 2y - 3z + 1 = 0
Tọa độ giao điểm của d và (a) nghiệm đúng hệ phương trình:
X = 1 + 3t
• y = -1 + 2t	(1)
z = 3 - 5t
6x-2y-3z + l = 0 (2)
Thế (1) vào (2) ta được:
6(1 + 3t) - 2(-l + 2t) - 3(3 - 5t) + 1 = 0
 t = 0
Suy ra giao điểm của đường thẳng d và mặt phẳng (ot) là điểm 1(1;-1; 3).
Gọi giao điểm của A và d là M. Do M e d nên M(1 + 3t; -1 + 2t; 3 - 5t).
Mặt khác đường thẳng A đi qua A(-l; 2; -3) nên nó có vectơ chỉ phương là:
V = AM = (2 + 3t; -3 + 2t; 6 - 5t)
Đường thẳng A vuông góc với giá của vectơ ã khi và chỉ khi:
ã±vũ.v=o
 6(2 + 3t) - 2(-3 + 2t) - 3(6 - 5t) = 0 Suy ra đường thẳng A có vectơ chỉ phương là:
V = (2; -3; 6)
Vậy phương trình tham số của đường thẳng A là:
X = -1 + 2t • y = 2 - 3t z = -3 + 6t
Bài 8. Viết phương trình mặt phẳng (a) tiếp xúc với mặt cầu (S): X2 + y2 + z2 - lOx + 2y + 26x + 170 = 0
và song song với hai đường thẳng
d:
X = -7 + 3t y = -1 - 2t z = 8
X = -5 + 2t y = 1 - 3t ; d': z = -13 + 2t
Giải
Mặt cầu (S) có tâm 1(5; -1; -13) và có bán kính là R = 5.
Đường thẳng d và d' có vectơ chỉ phương lần lượt là
ũ = (2; -3; 2), V = (3; -2; 0).
Mặt phẳng (a) song song với d và d' nên có vectơ pháp tuyến là: n = ũ A V = (4; 6; 5)
Suy ra phương trình của mặt phẳng (a) có dạng:
4x + 6y + 5z + D = 0
Mặt phẳng (a) tiếp xúc với mặt cầu (S) khi và chỉ khi:
|4.5 + 6.(-l) + 5.(-13) + D| d(I, (a)) = R J4	ì = 5
V42 + 62 + 52 1-51 + D| = 5777
Do đó: D = 51 + 5777 hoặc D = 51 - 5^77 Vậy phương trình của mặt phẳng (a) là:
4x + 6y + 5z + 51 + 5777 = 0
hoặc 4x + 6y + 5z + 51 — 5 777 = 0
Bài 9. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(l; -1; 2) trên mặt phảng (a): 2x - y + 2z + 11 = 0.
Giải
Mặt phẳng (a) có vectơ pháp tuyến n = (2; -1; 2). Gọi A là đường thẳng đi qua điểm M(l; -1; 2) và vuông góc với (ct), thì H là giao điểm của A và (oc). Vì A ± (a) nên ĩĩ là vectơ chỉ phương của A.
Phương trình tham số của A là:
X = 1 + 2t < y = -1-t (*)
z = 2 + 2t
Tọa độ điểm H ứng với t nghiệm đúng phương trình:
2(1 + 2t) - (-1 - t) + 2(2 + 2t) + 11 = 0
 t = -2
Thế t = -2 vào phương trình (*) ta được H(-3; 1; -2).
Bài 10. Cho điểm M(2; 1; 0) và mặt phẳng (a): X + 3y - z - 27 = 0. Tìm tọa độ điểm M' đối xứng với M qua (a).
Giải
Mặt phẳng (a) có vectơ pháp tuyến n = (1; 3; -1). Gọi A là đường thẳng đi qua điểm M(2; 1; 0) và vuông góc với (a), thì n là vectơ chỉ phương của A.
Phương trình tham sô của A là:
X = 2 + t • y = 1 + 3t (*)
z = -t
Gọi H là hình chiếu vuông góc của M trên mặt phẳng (oc) thì H là giao điểm của A và (a). Tọa độ của điểm H ứng với nghiệm đúng phương trình:
(2 + t) + 3(1 + 3t) - (-t) - 27 = 0 t = 2
Thế t = 2 vào phương trình (*) ta được H(4; 7; —2).
Vì M' là điểm đối xứng của M qua mặt phẳng (a) nên H là trung điểm của đoạn thẳng MM'.
Gọi M'(x0; yo; Zo) thì ta có:
x0 =2xh-xm =2.4-2 = 6
•y0 = 2yH-yM = 2.7-1 = 13
z0 = 2zh - ZM = 2.(-2) - 0 = -4 Vậy M'(6; 13; -4).
11. Viết phương trình đường thẳng A vuông góc với mặt phẵng tọa độ Oxz và cắt hai đường thẳng.
d:
X = 1 - 2t' y = -3 + t' z = 4 - 5t'
X = t
y = -4 + t ; d': z = 3 - t
Giải
Giả sử đường thẳng A cắt đường thẳng d tại điểm M và cắt đường thẳng d' tại điểm M'.
Ta có: M e d => M(t; -4 + t; 3 - t),
M' e d' => M'(l - 2t'; -3 + t'; 4 - 5t')
Như thế đường thẳng A có vectơ chỉ phương là:
ũ = MM' = (1 - t - 2t'; 1 - t + t'; 1 + t - 5t')
Do vậy, đường thẳng A vuông góc với mp(Oxz) khi và chỉ khi:
Từ (1) và (3) suy ra: t = Ệị, t' = ỹ và ta được:
(3
25
18ì
- ín-6-nì
— *
—
—
, u = 0 — 0
7
l 7 J
Vectơ ũ cùng phương với vectơ j = (0; 1; 0).
Vậy phương trình tham số của đường thẳng A là:
Tìm tọa độ điểm A' đối xứng với điểm A(l; -2; -5) qua đường thẳng A có phương trình:
X - 1 + 2t y = -l-t z = 2t
Giải
Đường thẳng A có vectơ chỉ phương ữ = (2; -1; 2). Gọi (a) là mặt phẳng đi qua điểm A(l; -2; -5) và vuông góc với A thì ũ là vecto' pháp tuyến của (a).