Giải Toán 12: Bài 2. Khối đa diện lồi và khối đa diện đều

§2. KHỐI ĐA DIỆN Lồi VÀ KHÔI ĐA DIỆN ĐỂU
A. KIẾN THỨC CẦN NHỚ
Khối đa diện lồi
Khôi đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
Khối đa diện đểu
Một khối đa diện lồi được gọi là khối đa diện đều loại {p, q} nếu:
Mỗi mặt của nó là một miền đa giác p cạnh.
Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Có đúng 5 loại khôi đa diện đều đó là: khối tứ diện đều, khôi lập phương khôi 8 mặt đều, khối 12 mặt đều, khối 20 mặt đều.
B. BÀI TẬP
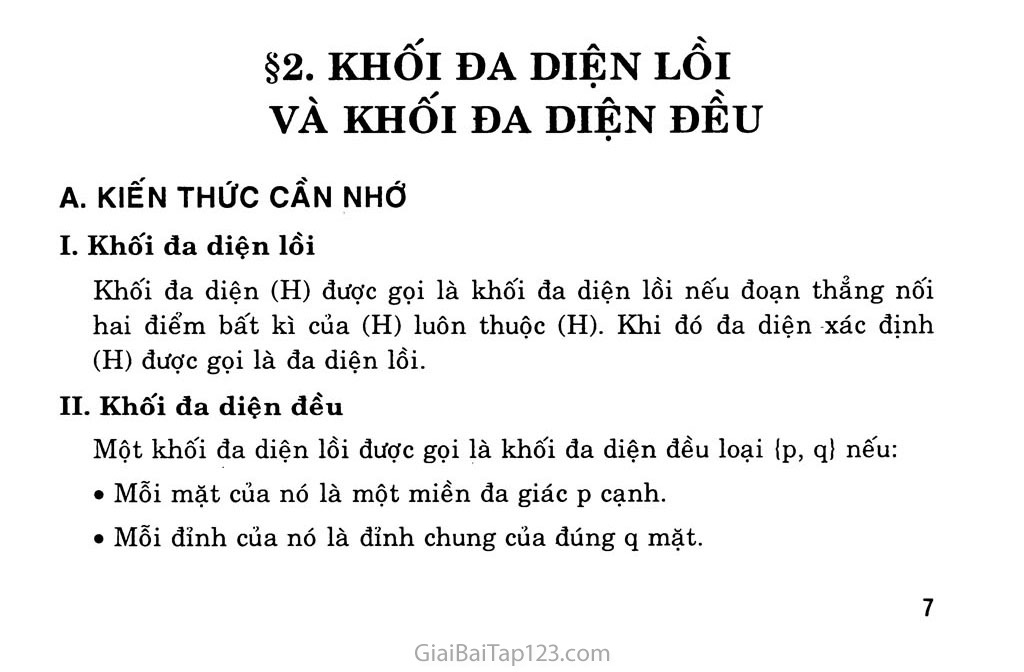
Bài 1. Cắt bìa theo mẫu dưới đây, gấp theo đường kẻ, rồi dán các mép
lại để được một hình tứ diện đều, hình lập phương và bát diện đều.
Bài tập này độc giả tự thực hiện.
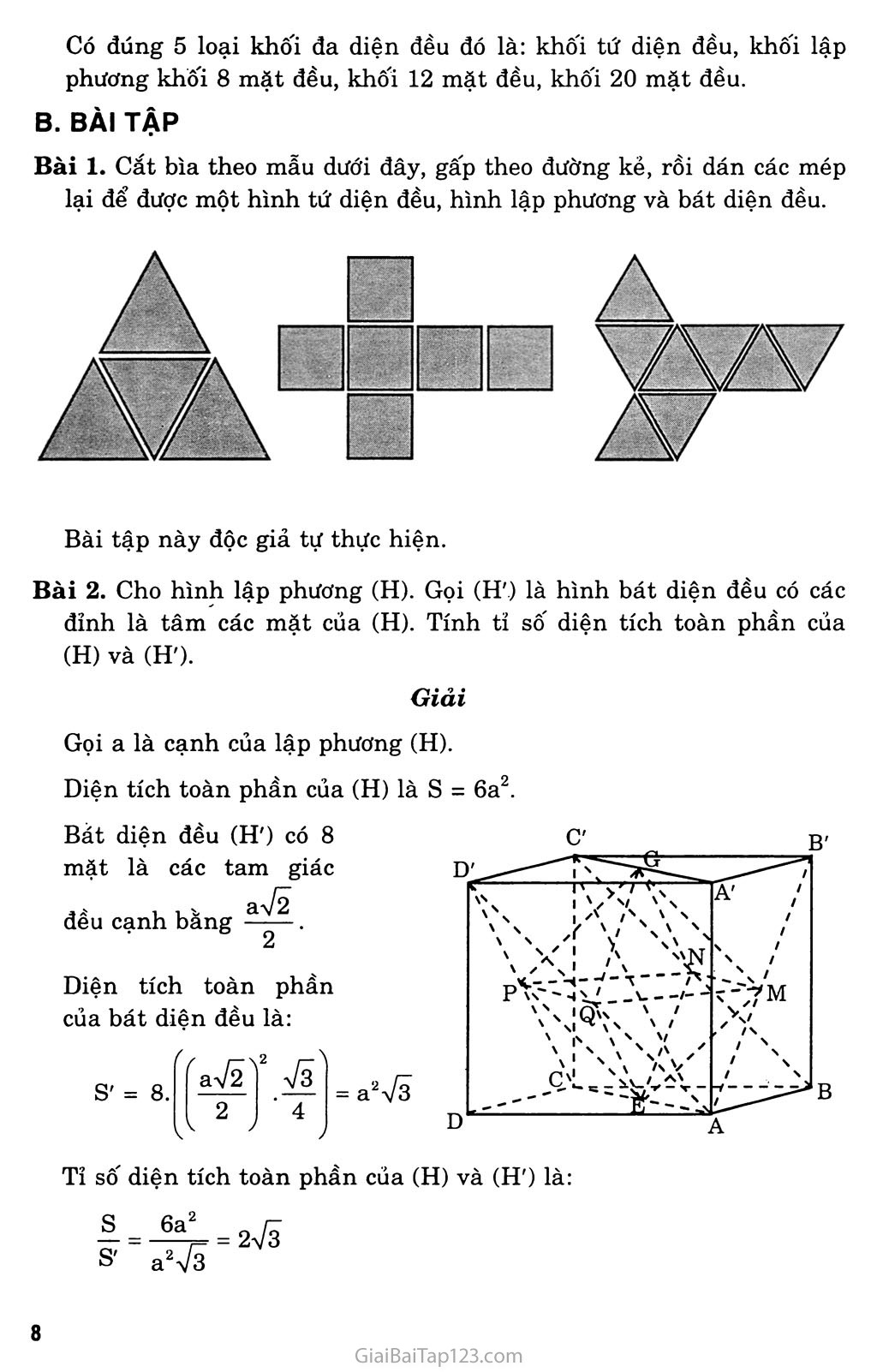
Bài 2. Cho hình lập phương (H). Gọi (H'.) là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H').
Giải
Gọi a là cạnh của lập phương (H).
Diện tích toàn phần của (H) là s = 6a2.
Bằt diện đều (H') có 8 mặt là các tam giác 	UX	a>/2
đêu cạnh băng 2
Diện tích toàn phần của bát diện đều là:
S' = 8.
av2 V3 4
= 2V3
Tỉ số’ diện tích toàn phần của (H) và (H') là:
s 6a2 S' - a2VI
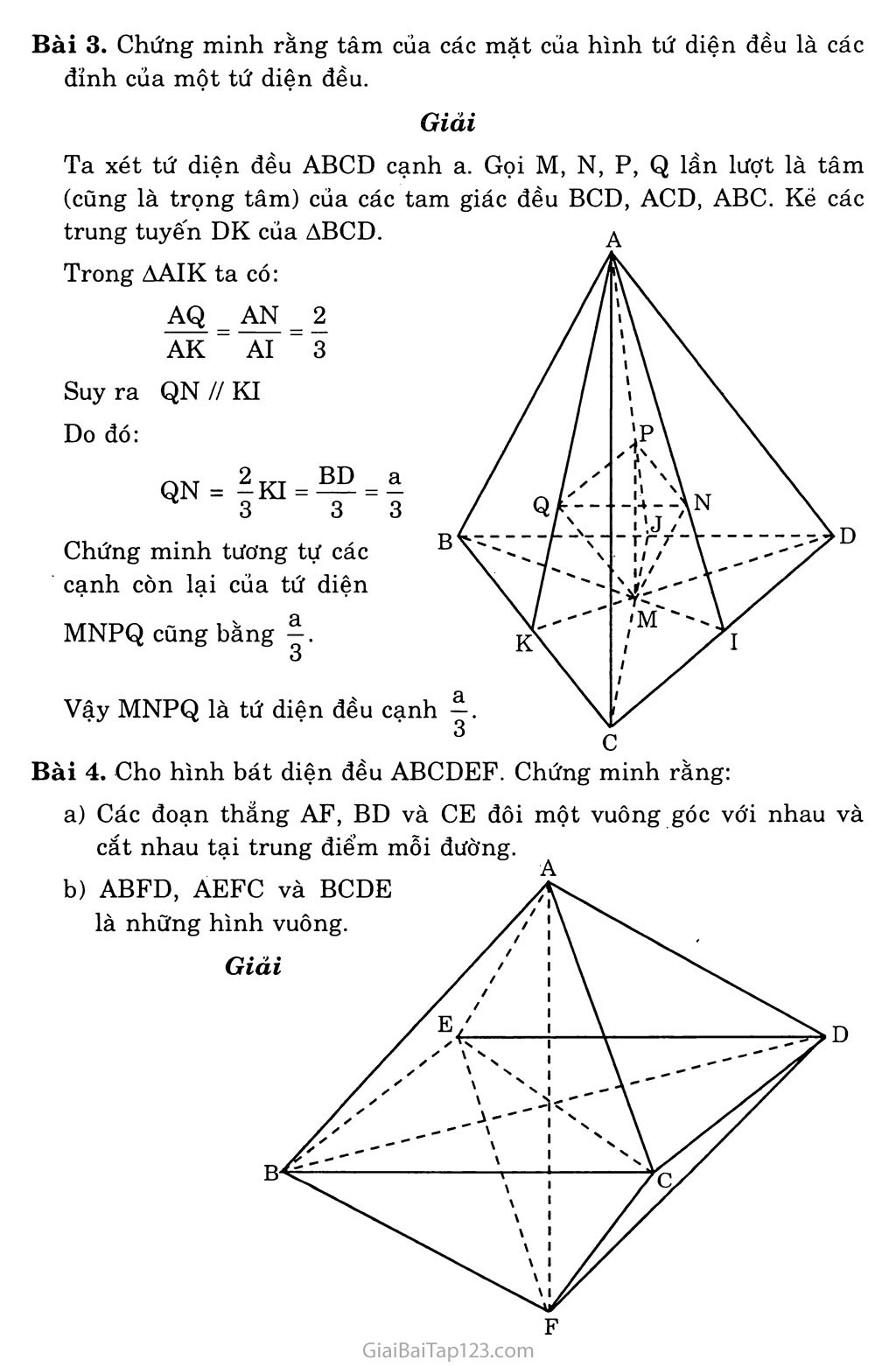
Bài 3. Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một tứ diện đều.
Giải
Ta xét tứ diện đều ABCD cạnh a. Gọi M, N, p, Q lần lượt là tâm (cũng là trọng tâm) của các tam giác đều BCD, ACD, ABC. Kẻ các trung tuyến DK của ABCD.
Trong AAIK ta có:
AQ AN _ 2 AK AI - 3
Suy ra QN//KI
Do đó:
QN = ^KI = ^ = | 3	3	3
Chứng minh tương tự các cạnh còn lại của tứ diện
MNPQ cũng bằng Ệ-.
3
Vậy MNPQ là tứ diện đều cạnh
Bài 4. Cho hình bát diện đều ABCDEF. Chứng minh rằng:
Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
ABFD, AEFC và BCDE là những hình vuông.
Giải
Gọi a là cạnh của bát diện đều ABCDEF, từ giả thiết suy ra:
BA = BF = a, CA = CDD = a, DA = DF = a, EA = EF = a
Do đó các điểm B, c, D, E cùng nằm trên mặt trung trực (P) của đoạn thẳng AF, tức là bốn điểm B, c, d, E đồng phẳng. Gọi o là giao điểm của AF và mặt phẳng (P) thì AF vuông góc với mặt phẳng (P), o là trung điểm của AF.
Ta có: BC = CD = DE = EB = a nên tứ giác BCDE là hình thoi.
Mặt khác AO vuông góc mặt phẳng (P) và AB = AC = AD = AE nên OB = oc = OD = OE.
Suy ra BCDE là hình vuông và o là giao điểm của BD và CE.
Từ các kết quả trên ta dễ dàng suy ra: ba đoạn thẳng AF, BD, CE vuông góc với nhau từng đôi một và chúng cắt nhau tại điểm o là trung điểm của mỗi đường.
Theo chứng minh trên BCDE là một hình vuông. Chứng minh tương tự ta được AEFC, ABFD là các hình vuông.