Giải Toán 12: Ôn tập chương I

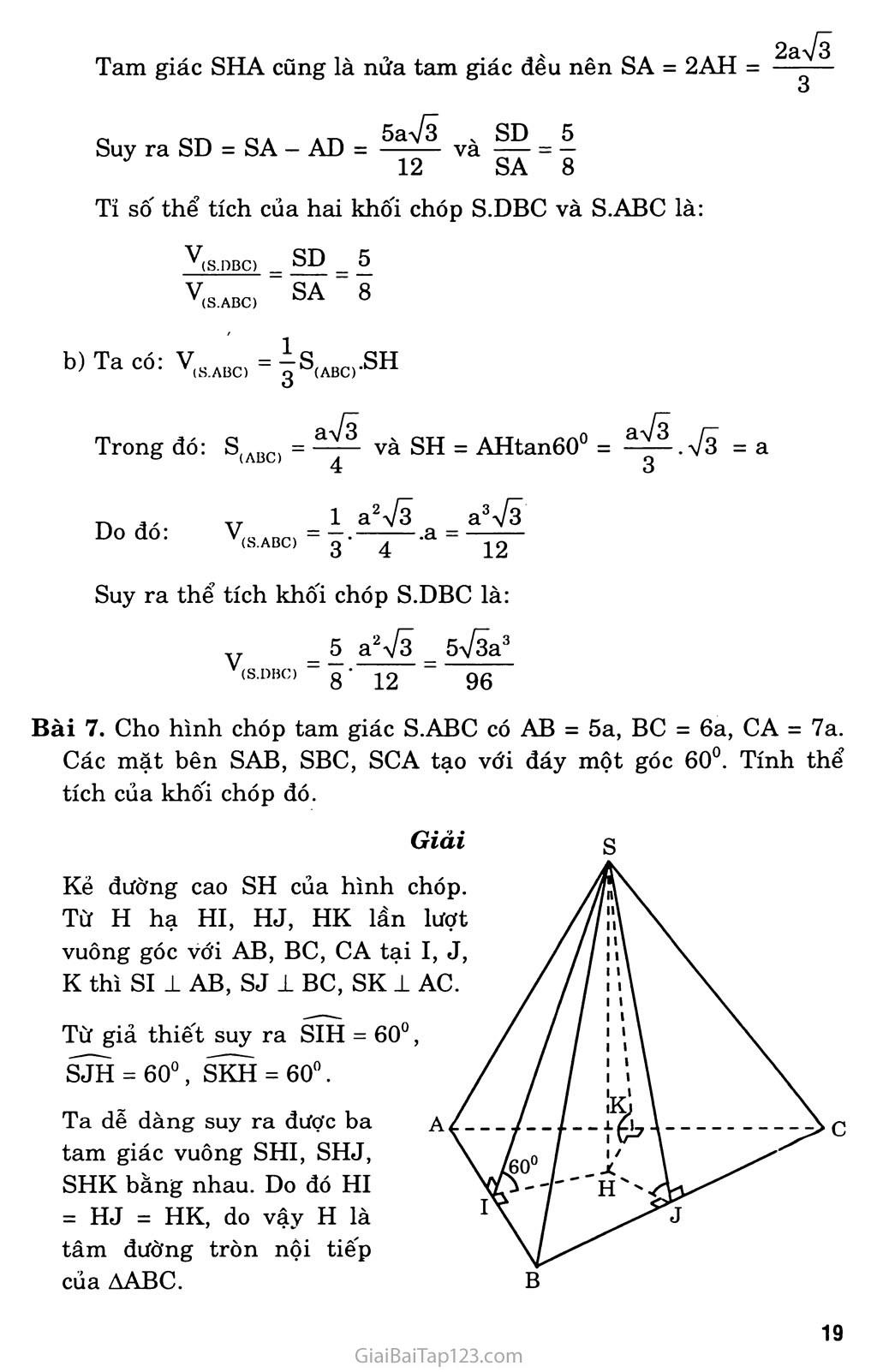
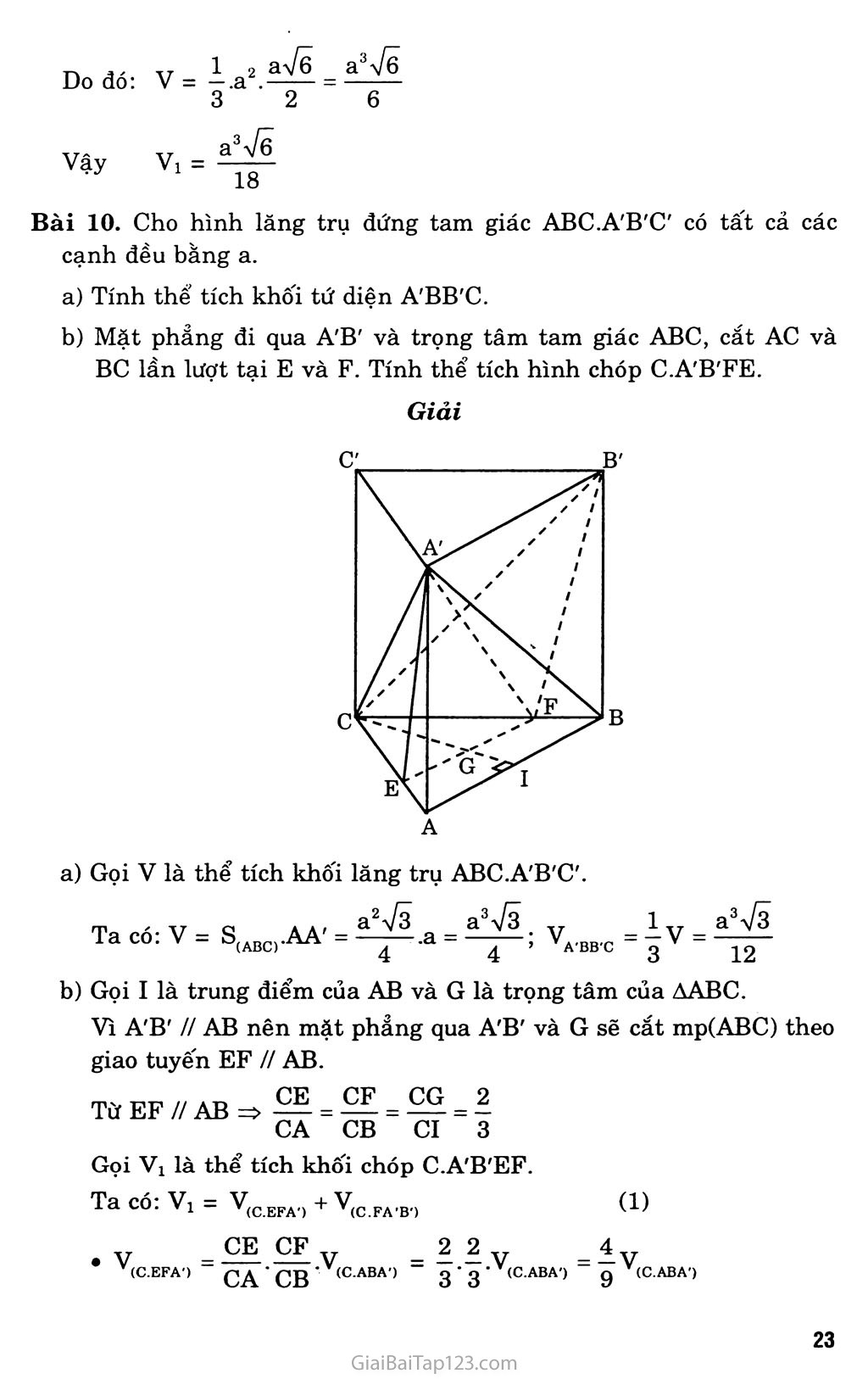
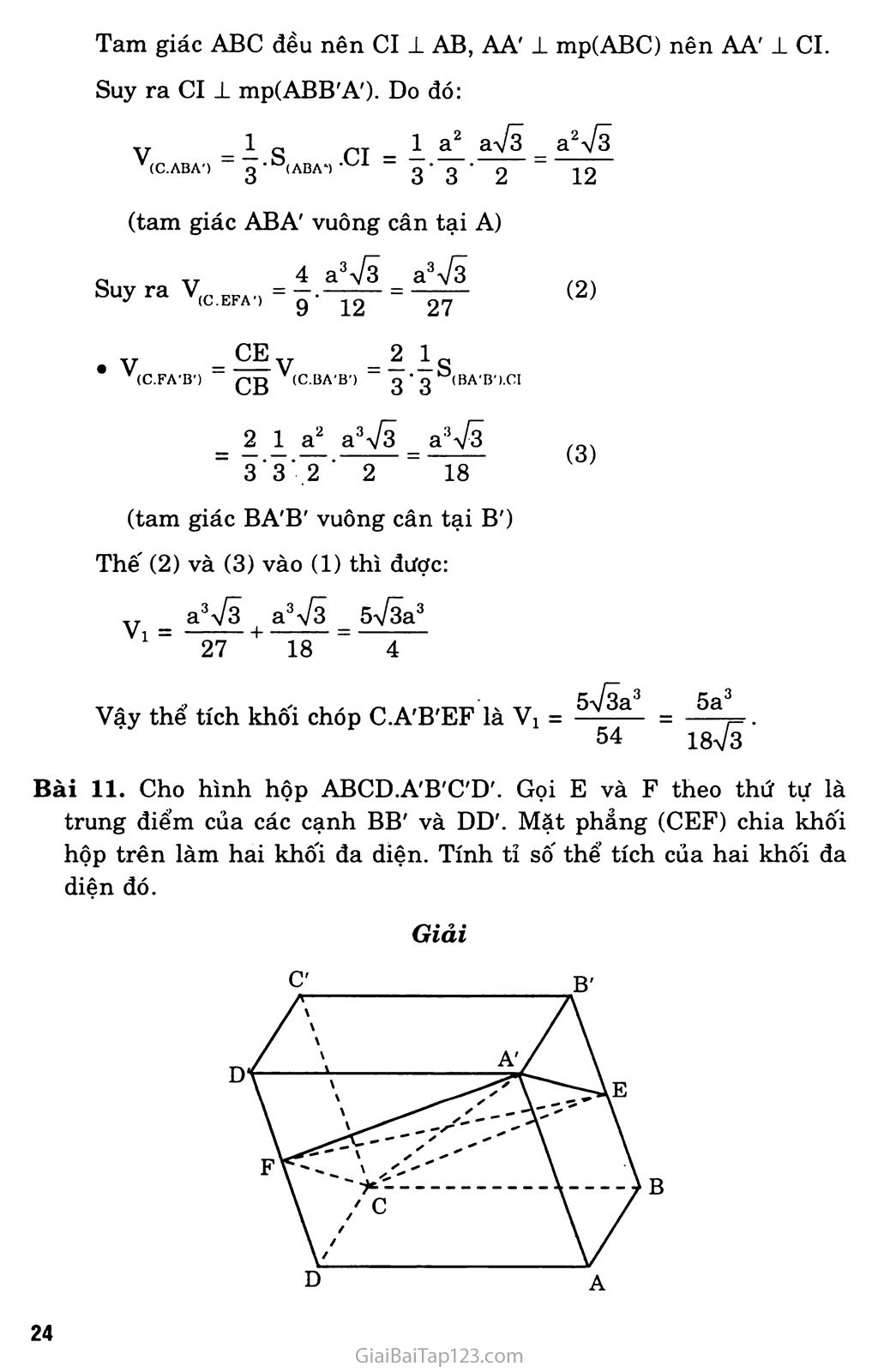
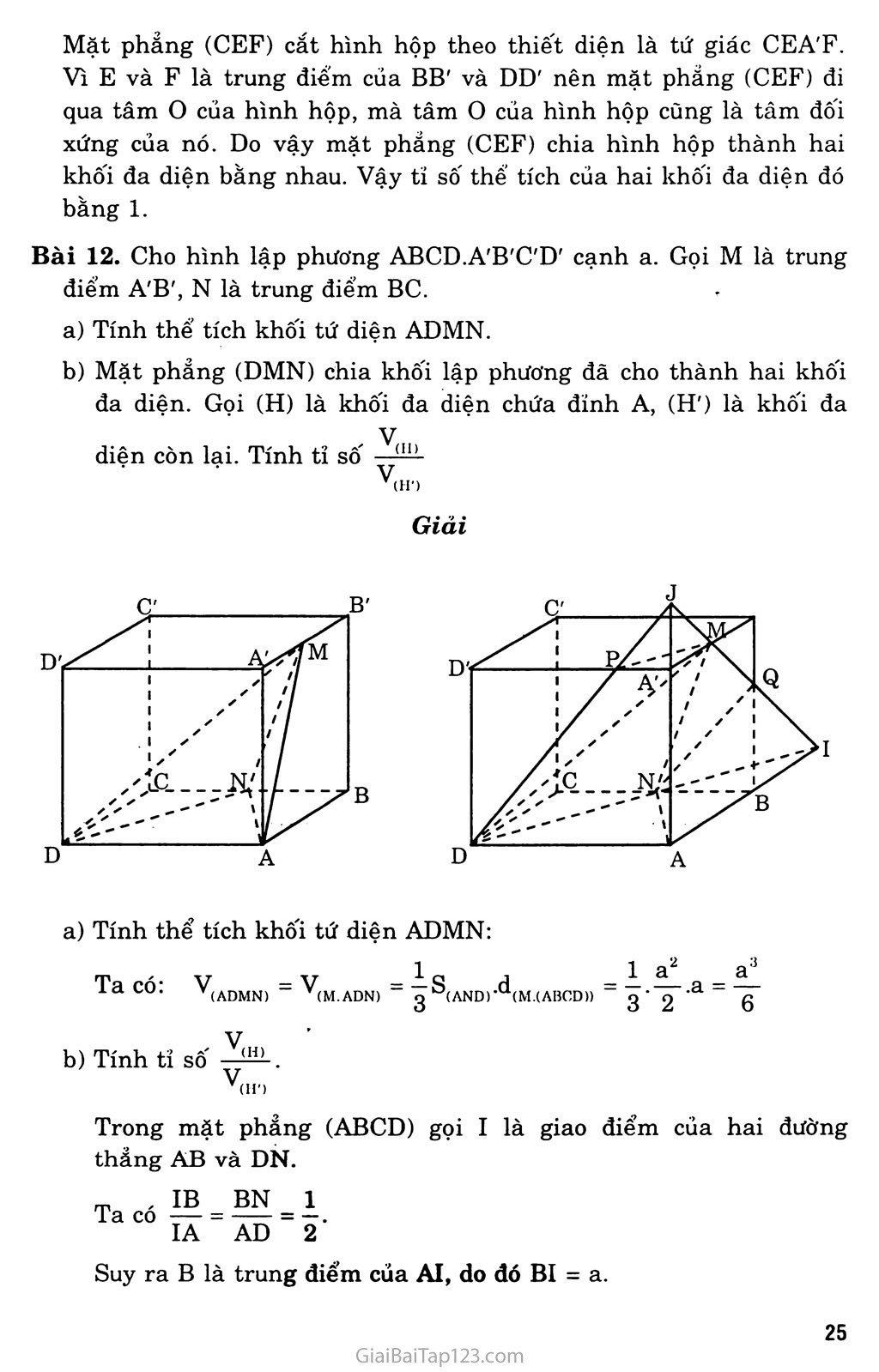
ÔN TẬP CHƯƠNG I
Bài 1. Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất nào?
Giải
Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn tính chất sau:
Hai mặt phân biệt chỉ có thế’ hoặc không giao nhau, hoặc có một đỉnh chung, hoặc có một cạnh chung.
Mỗi cạnh thuộc một mặt là cạnh chung của đúng hai mặt.
Cho hai mặt s và S', luôn tồn tại một dãy các mặt So, Si,..., s„ sao cho So trùng với s, s„ trùng với S' và bất kì hai mặt Si, Si+1 nào (0 < 1 < n - 1) cùng đều có một cạnh chung.
Bài 2. Tìm một hình tạo bởi các đa giác nhưng không phải là một đa diện.
Lây hình (H) như hình bên, hình này gồm có hai hình chóp có chung một đỉnh. Ta thấy hình (H) này có các mặt là các đa giác, nhưng nó không phải là một đa diện.
Bài 3. Thế nào là một khôi đa diện lồi? Tìm ví dụ trong thực tế mô tả một khối đa diện lồi, một khôi đa diện không lồi.
Giải
Một khối đa diện (H) được gọi là một khôi đa diện lồi nếu đoạn thẳng nốì hai điểm bât kì của (H) luôn thuộc (H).
Các hộp đựng bánh, kẹo ngoài thị trường thường có dạng một khôi hộp chữ nhật. Khôi hộp chữ nhật là một khôi đa diện lồi.
Viên gạch lát nền nhà có dạng một khôi lăng trụ tứ giác đều. Khôi lăng trụ tứ giác đều là một khôi đa diện lồi.
Khung cửa sổ bằng gỗ có dạng một khôi đa diện. Khối đa diện này không lồi.
(khung cửa sổ)
Bài 4. Cho hình lăng trụ và hình chóp có diện tích đáy và chiều cao bằng nhau. Tính tỉ số có thể tích của chúng.
Giải
Gọi s là diện tích đáy và h là chiều cao của khối lăng trụ và khối chóp, và gọi Vi, v2 lần lượt là thể tích của chúng.
Ta có: J- =	= 3
Vs jsh 3
Vậy tỉ số thể tích của khối lăng trụ và khối chóp có diện tích đáy và chiều cao bằng nhau là 3.
Bài 5. Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, oc đôi một vuông góc với nhau và OA = a, OB = b, oc = c. Hãy tính đường cao OH của hình chóp.
Giải
Kẻ đường cao OH của hình chóp, kéo dài CH cắt AB tại I.
Từ giả thiết ta có:
■ Ỷ	oc ra AB 1 oc
 mp(OAB)
oc 1 OB
(1)
Mà
OH ± mp(ABC) =>
OH 1 CI OH 1 AB
Từ (1) và (2) ta được AB ± mp(OCI) Do đó AB ± CI và AB 1 OI
Dễ thấy AOCI vuông tại o.
Áp dụng hệ thức lượng trong AOCI.
Ta có:	—=	—^r +	(3)
OH2	oc2 OI2
Từ AOAB vuông tại O:
1 =	1 1	f4)
OI2 OA2 + OB2
Kết hợp (3) và (4) ta được:
1	_	1	1 _JL_
OH2 " OA" + OB2 + oc2
1	1	1 _ b2c2
- a2 + b2 + c2 -
+ c2a2 + a2b2 a2b2c2
Vậy chiều cao của hình chóp là: OH =
abc
Va2b2 + b2c2 + c2a2
c
Bài 6. Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, sc tạo với đáy một góc 60°. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA.
Tính tỉ số thể tích của hai khôi chóp S.DBC và S.ABC.
Tính thể tích của khôi chóp S.DBC.
Giải
a) Kẻ đường cao SH của hình chóp, thì H là tâm của AABC và gọi I là trung điểm của BC.
Từ giả thiết suy ra SAH - 60°
Ta có:
BC 1 AI
‘ BC1SH
=> BC ± mp(SAI).
Do đó từ giả thiết SA 1 mp(BCD) => SA ± DI.
Như vậy ADAI là nửa tam giác
đều, suy ra: AD = 4 AI =
c
2	4
Tam giác SHA cũng là nửa tam giác đều nên SA = 2AH =
Suy ra SD = SA - AD = ^ệ- và = I J	12 SA 8
2aVã
V,
V,
(S.DBC)
(S.ABC)
SD
SA
Tỉ số thể tích của hai khôi chóp S.DBC và S.ABC là:
b) Ta có: V(SABC) = |s(ABC).SH
Trong đó: s
(ABC)
và SH = AHtan60° =	= a
Do đó:
V
(S.ABC)
4
1 a2 Vã
-.a
a3 Vã
3	4	12
Suy ra thể tích khôi chóp S.DBC là:
V _ (S.DBC)
5 a2V3 5V3a3
8 12
96
Bài 7. Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA = 7a. Các mặt bên SAB, SBC, SCA tạo với đáy một góc 60°. Tính thể tích của khôi chóp đó.
Giải
Kẻ đường cao SH của hình chóp. Từ H hạ HI, HJ, HK lần lượt vuông góc với AB, BC, CA tại I, J, K thì SI 1 AB, SJ 1 BC, SK 1 AC.
Từ giả thiết suy ra SIH = 60°,
SJH = 60°, SKH - 60°.
Ta dễ dàng suy ra được ba tam giác vuông SHI, SHJ,
SHK bằng nhau. Do đó HI = HJ = HK, do vậy H là tâm đường tròn nội tiếp của àABC.
Ta có:
V — — s QU
V(S.ABC) _ g°(ABC)’Ori	k 7
Theo công thức Hê-rông
S(ABC) = ựp(p-a)(p-b)(p-c)
m	,,	~ 5a + 6a + 7a _
Irong đó: p =	—	 = 9a
p - a = 4a, p - b = 3a, p - c = 2a Suy ra:	S(ABC) = V9a.4a.3a.2a = ôVẽa2
A/TA	Q 	s c 6\/6a 2yỈ6a
Mà	S.AR„. = pr => r =	;	= - - ■
(ABC)	p 9a 3
(r là bán kính của đường tròn nội tiếp AABC)
Từ tam giác SHI vuông tại H cho:
SH = HI.tan60° = r.tan60° =	= 2^2a
3
Thế vào (*) ta được: V = 4.6ự6a2.2V2a = 8 Via3
Giải
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy và AB = a, AD = b, SA = c. Lấy các điểm B', D' theo thứ tự thuộc SB, SD sao cho AB' vuông góc với SB, AD' vuông góc với SD. Mặt phẳng (AB'D') cắt sc tại C'. Tính thể tích khối chóp S.AB'C'D'.
Từ giả thiết:
BC ± AB BC 1 SA
Gọi o là giao điểm của AC và BD, I là giao điểm của AC' và B'D', dễ thấy ba điểm s, o, I thẳng hàng.
=> BC ± mp(SAB), do đó BC ± AB' Kết hợp với AB' ± SB ta được
AB' 1 mp(SBC)
Suy ra AB' ± sc	(1)
Chứng minh tương tự: AD' 1 mp(SCD) và AD' 1 sc (2)
Từ (1) và (2) cho SC 1 mp(AB'C'D') => sc 1 AC'
Gọi V, V' lần lượt là thể tích của khôi chóp S.ABCD và S.AB'C'D'. Khối chóp S.ABCD có thể tích là:
SB
_	 SB' SA2 c2
Suy ra: —— = ■ = —T-—õ
SB SB2 a + c2
o	 SC' SA2	C
Suy ra: —- =	- ———	-
SC SC2 a2+b +C Thế vào (4) ta được:
V
(S.ABV) a2+c2‘a2 + b2+c2'2 Chứng minh tương tự ta được:
y	 ỉ /ab
V(S.ACD3 6(b2+c2)(a2+b2+c2)
Thế (5) và (6) vào (3):
c5ab
Chứng minh tương tự, từ tam giác SAC vuông tại A ta có:
-ệệ .	,	(5,
6(a2 + c2)(a2 + b2 + c2)
(6)
V' -	+	c5ab
6(a2 + c2)(a2 + b2 + c2)	6(b2 + c2)(a2 + b2 + c2)
' abc5(a2 + b2 + 2c2)
" 6(a2 + c2)(b2 + c2)(a2 + b2 + c2)
Vậy thể tích khôi chóp S.AB'C'D' là:
= abc5(a2 +b2 +2c2)
" 6(a2 + c2)(b2 + c2)(a2 + b2)
Giải
Bài 9. Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60°. Gọi M là trung điểm sc. Mặt phảng đi qua AM và song song với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khôi chóp S.AEMF.	g
Kẻ đường cao SH của khôi chóp S.ABCD thì H là giao điểm của AC và BD.
Từ giả thiết suy ra:
SAH = SBH = SCH = SDH = 60°
Như thế các mặt chéo của hình chóp là tam giác đều. A
Gọi I là giao điểm của AM và EF, dễ thấy I e SH.
Do (a) // BD nên (a) cắt (SBD) theo giao tuyến PQ // BD.
Ta có:	1 AC => BD 1 (SAC)
(BD 1 SH
Mà EF // BD nên EF 1 (SAC), suy ra EF 1 AM.
Vậy tứ giác AEMF có hai đường chéo vuông góc.
Ngoài ra do H là trung điểm của BD nên I cũng là trung điểm của EF, nghĩa là hai điểm E và F đối xứng với nhau qua AM.
Vì M là trung điểm của sc nên SH và AM là các trung tuyến của ASAC, do đó I là trọng tâm của ASAC.
rp	Aũnn.	TPT? // DPI	■	SE	SF	SI	2
Trong	ASBD:	EF // BD	=>	==—	=	77=-	= 7777	= ==
6	SB	SD	SH	3
Gọi Vi là thể tích khôi	chóp	S.AEMF	và là thể tích khôi chóp
S.ABCD ta có:
V, = 2V,O .... = 2 SE SM	= O 2 1 V = 1 v
1 (S.AEM) 2. gB . sc,. (S.ABC) 2- 3 • 2 • 2	3 v
Mặt khác V = ==.S(ABCD).SH, trong đó:
3
(ABCD)
= a\ SH =
Acựi _ aựẽ
T~\ Ji. XT 1 „2 aVô a3V6
Do đó: V = -E-.a r— = —-7— 3	2	6
I3 Vẽ
18
Vậy Vi =
Bài 10. Cho hình lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a.
Tính thể tích khôi tứ diện A'BB'C.
Mặt phảng đi qua A'B' và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Tính thể tích hình chóp C.A'B'FE.
Giải
b) Gọi I là trung điểm của AB và G là trọng tâm của AABC.
Vì A'B' // AB nên mặt phẳng qua A'B' và G sẽ cắt mp(ABC) theo giao tuyến EF // AB.
CA CB CI 3
Gọi Vi là thể tích khối chóp C.A'B'EF.
Ta có: Vi = V(C EFA>) + V(C FA,B1)	(1)
02^ ’ 02 * (C.ABA') 2	2 (C.ABA') 0 (C.ABA')
(C.EFA')
CE CF
Tam giác ABC đều nên CI ± AB, AA' 1 mp(ABC) nên AA' ± CI. Suy ra CI 1 mp(ABB'A'). Do đó:
Y _ 1 Q |-1T _ 1 a a-\Ỉ3 a“V3
V(C.ABA') - q -Ữ(ABA‘) ■Lyi - q- q • ọ - 19
= 4 a3VI _ a3V3 ’(C.EFA’)	9’ 12	27
(tam giác ABA' vuông cân tại A)
(2)
(3)
Suy ra V..
• V,P™ = ^V.r„.,R,. = — . — S,
(C.FA’B') Qg (C.BA B’) g • g‘-’(BA'B').CI
= 2 1 a? a\/| = a\/3 3 3 2 ' 2	18
(tam giác BA'B' vuông cân tại B') Thế (2) và (3) vào (1) thì được:
„ _ a3VI , a3V3 _ õVãa3 27	18	4
Vậy thể tích khối chóp C.A'B'EF là V! =
54	18^3
Bài 11. Cho hình hộp ABCD.A'B'C'D'. Gọi E và F theo thứ tự là trung điểm của các cạnh BB' và DD'. Mặt phẳng (CEF) chia khối hộp trên làm hai khôi đa diện. Tính tỉ số thể tích của hai khối đa diện đó.
Giải
Mặt phẳng (CEF) cắt hình hộp theo thiết diện là tứ giác CEA'F. Vì E và F là trung điểm của BB' và DD' nên mặt phẳng (CEF) đi qua tâm o của hình hộp, mà tâm o của hình hộp cũng là tâm đối xứng của nó. Do vậy mặt phẳng (CEF) chia hình hộp thành hai khôi đa diện bằng nhau. Vậy tỉ số thế tích của hai khôi đa diện đó bằng 1.
Bài 12. Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M là trung điểm A'B', N là trung điểm BC.
Tính thể tích khôi tứ diện ADMN.
Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khôi đa diện. Gọi (H) là khôi đa diện chứa đinh A, (H') là khối đa
V,,,.
diện còn lại. Tính tỉ số -d11’
V,,.,
(H’>
Giải
Ta co: V(ADMN) \m.adn) g S(AND)-d<M (ABCD)) 3 ■ 2 'a 6 v.,„
b) Tính tỉ số
V.
V(H')
Trong mặt phẳng (ABCD) gọi I là giao điểm của hai đường thẳng AB và DN.
, IB _ Ta có £— =
IA
BN
AD
Suy ra B là trung điểm của AI, do đó BI = a.
Trong mặt phẳng (ABA'B'), gọi J và Q lần lượt là giao điểm của đường thẳng MI với hai đường thẳng AA' và BB'. Trong mặt phẳng ADD'A' gọi p là giao điểm của DJ và A'D'. Như vậy ngũ giác DNQMP là thiết diện của lập phương ABCD.A'B'C'D' cắt bởi mặt phẳng (DMN).
BI // MB' =>	= A
QB BI 2
»
Suy ra BQ = —
. AOUT // AT _ JA' A'M 1
A'M // AI =>	= -73- = —.
JA AI 4
Suy ra JA' = A'P =	.
3	4
Tính thể tích của khôi đa diện (H).
Ta có V... - V	 IV	_ + V 1
(H) V(J.ADI) L (Q.BNI) (,J.A’MP)J
+ V(J.ADI) = ~AD.AI.AJ — — ,a.2a.—— = —— 6	6	3	9
TT	1 TÍT DAT TI 1 _ <3- 2â a.
+ Vq.bnd - 5BI.BN.BQ	= 5
a3
144
Do đó V(H) =
4a3
9
89a3
144
a a 18 + 144
55a3
144
Suy ra V(H>)
55 89 ■
+ V.J.A-MP