Giải Toán 12: Ôn tập cuối năm

ÔN TẬP CUỐI NĂM
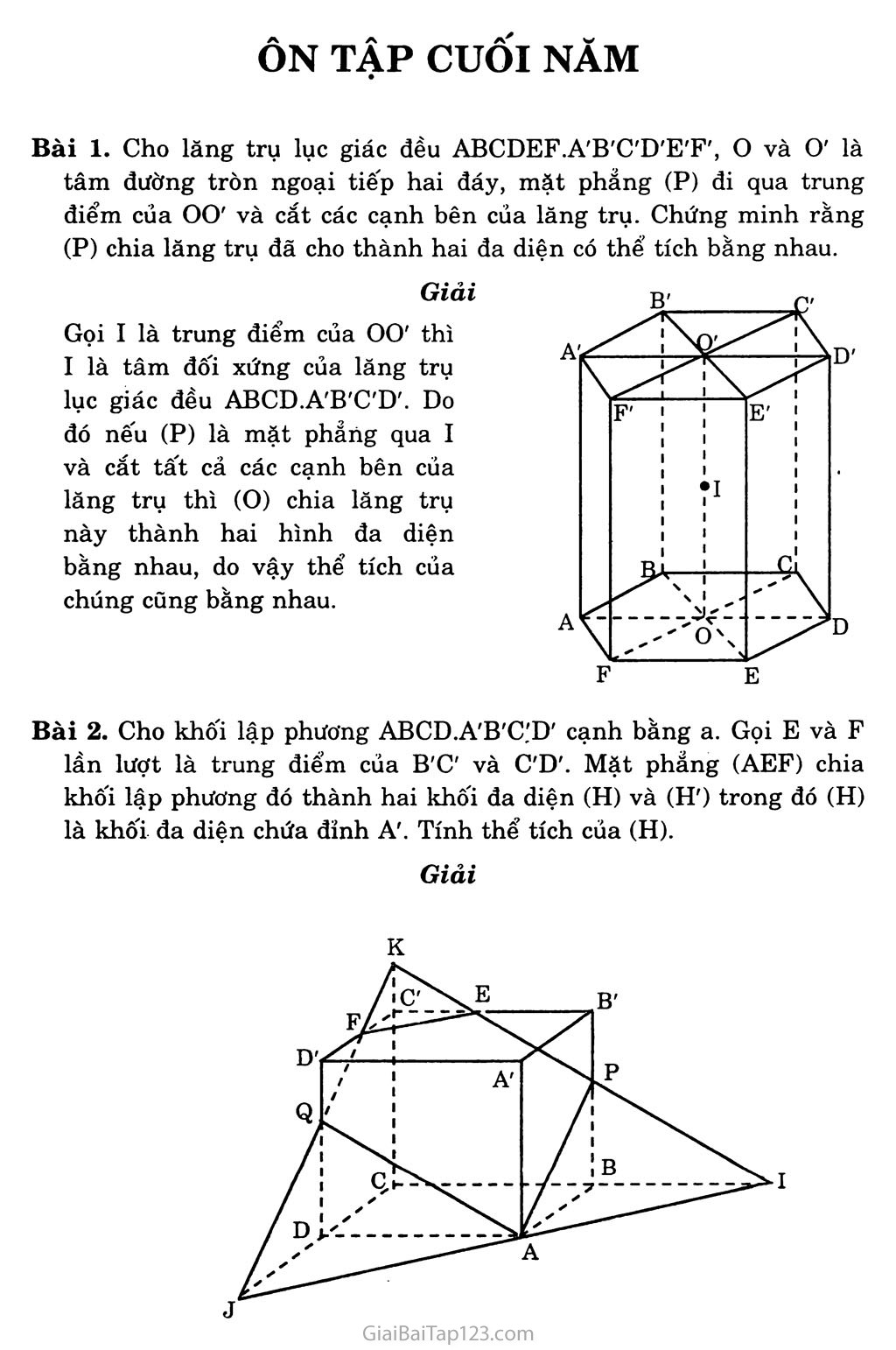
Bài 1. Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F', o và O' là tâm đường tròn ngoại tiếp hai đáy, mặt phẵng (P) đi qua trung điểm của OO' và cắt các cạnh bên của lăng trụ. Chứng minh rằng (P) chia lăng trụ đã cho thành hai đa diện có thể tích bằng nhau.
Gọi I là trung điểm của 00' thì I là tâm đối xứng của lăng trụ lục giác đều ABCD.A'B'C'D'. Do đó nếu (P) là mặt phẳiig qua I và cắt tất cả các cạnh bên của lăng trụ thì (O) chia lăng trụ này thành hai hình đa diện bằng nhau, do vậy thể tích của chúng cũng bằng nhau.
Bài 2. Cho khối lập phương ABCD.A'B'C.'D' cạnh bằng a. Gọi E và F lần lượt là trung điểm của B'C' và C'D'. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A'. Tính thể tích của (H).
Giải
Mặt phẳng (AEF) cắt mp(ABCD) theo giao tuyến là đường thẳng d qua a và song song với EF. Gọi I và J lần lượt là giao điểm của d với các đường thẳng BC và CD. Gọi p và K lần lượt là giao điểm của đường thẳng IE với các đường thẳng BB' và CC' và gọi Q là giao điểm của FJ và DD'. Ngũ giác APEFQ là thiết diện của hình lập phương cắt bởi mặt phảng (AEF).
Ta có:
+ AB // CJ =>	= ị. Suy ra IB = a.
CJ IC 2
+ BI // EB'	= 2. Suy ra PB =
2a
T
PB' B'E	3
Tương tự ta cũng có DJ = a và QD =
+ Hai tam giác vuông B'EP và C'EK bằng nhau, do đó KC' = PB' =
3
Gọi Vi, v2 là thể tích của (H) và (H') và V là thể tích của khôi lập phương. Ta có:
+ V = a3.
+ v2 = V(CIJK) - (V(BAIP) + V(DAJQ) + V(CEFK)
Mà:
V(CUK> = jci.CJ.CK = i.2a.2a.^ = 6	6	3
V(BAIP, = |aB.BI.BP = ị.a.a.^ = ị- 6	6	3	9
V(ƠEFK. = ịc'E.C'F.CK = i J. J a = (CEFK) g	6 2 2 3
8a3
9
, V(ADÓQ) =
a?
72
Suy ra:
Suy ra:
Vi = a3 -
k
47a3
72
47a:!
72
25a3
72
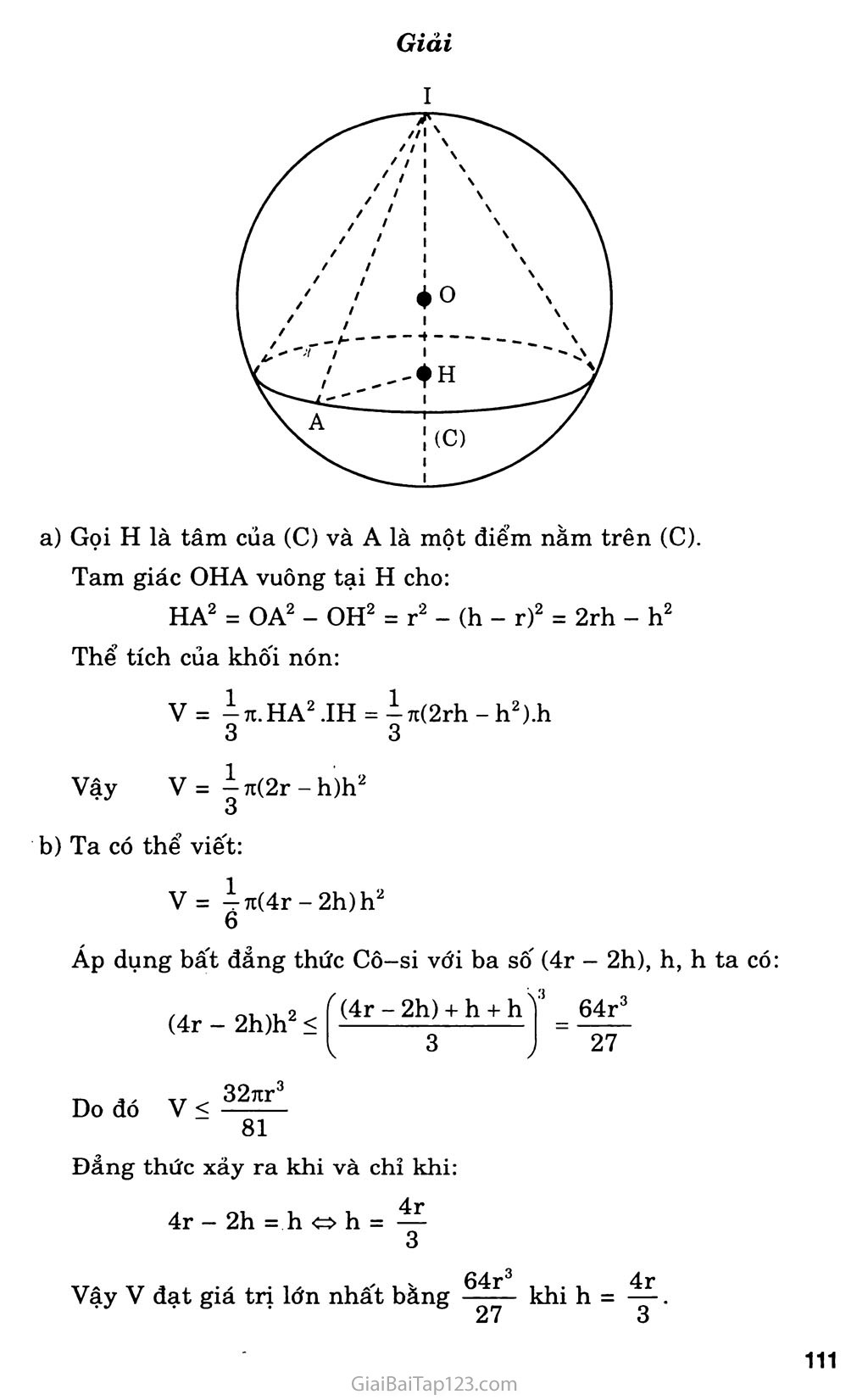
Bài 3. Cho mặt cầu (S) tâm o bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó.
Tính thể tích của hình nó .1 theo r và h.
Xác định h để thể tích của hình nón là lớn nhất.
Giải
a) Gọi H là tâm của (C) và A là một điểm nằm trên (C). Tam giác OHA vuông tại H cho:
HA2 = OA2 - OH2 = r2 - (h - r)2 = 2rh - h2 Thể tích của khối nón:
v = ịn.HA2-IH = 4rc(2rh - h2).h 3	3
Vậy V = ^7t(2r-h)h2 3
b) Ta có thể viết:
V = 4n(4r-2h)h2 6
Áp dụng bất đẳng thức Cô—si với ba sô" (4r — 2h), h, h ta có:
\3 r. _3
Do đó V <
(4r - 2h)h2 <
327tr3
(4r - 2h) + h + h
64r
27
81
Đẳng thức xảy ra khi và chỉ khi:
4r - 2h = h h = 4-r 3
V 64r3 _	4r
Vậy V đạt giá trị lớn nhất bang	khi h =	.
27	3
Bài 4. Trong không gian Oxyz, cho hai điểm A(l; 2; -1), B(7; -2; 3) X = -1 + 3t
y = 2 - 2t z = 2 + 2t
và đường thẳng d có phương trình:
Chứng minh rằng hai đường thẳng d và AB cùng nằm trong một mặt phẳng.
Tìm điểm I trên d sao cho AI + BI nhỏ nhất.
Giải
Đường thẳng d đi qua điểm M(-1; 2; 2) và có vectơ chỉ phương ũ = (3; -2; 2).
Đường thẳng AB có vectơ chỉ phương AB = (6; -4; 4).
Suy ra AB = 2u	(1)
Thế tọa độ của A vào phương trình của d ta được:
ì = -1 + 3t • 2 = 2 - 2t
-1 = 2 + 2t
Ta thấy hệ trên vô nghiệm nên A(l; 2; -1) không thuộc d. (2) Từ (1) và (2) suy ra AB // d.
Vậy hai đường thẳng d và AB cùng nằm trên một mặt phẳng.
Gọi c là điểm đối xứng của A qua đường thẳng d.
Ta có IA = IB, do đó:
AI + BI = CI + BI > BC
Đẳng thức xảy ra khi và chỉ khi I nằm trên đoạn thẳng BC.
Như vậy I trùng với điểm lo là giao điểm của AB và d.
Mặt khác, do AB // d nên nếu gọi J là trung điểm của AB thì lo là hình chiếu vuông góc của J trên đường thẳng d.
Ta có: J(4; 0; 1).
Phương trình của mặt phẳng (a) đi qua J và vuông góc với d là: 2(x - 4) - 2(y - 0) + 2(z - 1) = 0
 3x - 2y + 2z - 14 = 0
Tọa độ của lo ứng với t nghiệm đúng phương trình:
3(-l + 3t) - 2(2 - 2t) + 2(2 + 2t) - 14 = 0
 t = 1
Suy ra I0(2; 0; 4).
Vậy khi I = I0(2; 0; 4) thì AI + BI đạt giá trị nhỏ nhất bằng:
BC = 2BI0 = 730
Bài 5. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC). Biết rằng AC = AD = 4 cm, AB = 3 cm, BC = 5 cm.
Tính thể tích tứ diện ABCD.
Tính khoảng cách từ điểm A tới mặt phảng (BCD).
Giải
Như vậy tam giác BCD cân tại B. Kẻ đường cao BH của ABCD thì H là trung điểm của CD.
Do đó:
BH = VbC2 - CH2 = ựõ2 -(2V2)2 = VĨỸ
Suy ra:
S,AECD, = jcD.BH = Ă.ếVã.VĨỸ = 2 734
Khoảng cách d tù’ A đến mặt phẳng (BCD) là:
3V 12
S(AABC) V34
(cm)
Bài 6. Trong không gian Oxyz cho mặt cầu (S) có phương trình:
X2 + y2 + z2 = 4a2
Tính diện tích mặt cầu (S) và thể tích của khôi cầu tương ứng.
Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Xác định tâm và bán kính của (C).
Tính diện tích xung quanh của hình trụ nhận (C) làm đáy và có chiều cao là a V3 . Tính thể tích của khôi trụ tương ứng.
Giải
Từ giả thiết suy ra mặt cầu (S) có tâm là gốc tọa độ o, bán kính R = 2a (a > 0).
Diện tích của mặt cầu (S):
S(m/c) = 4n.(2a)2 = 167ta2
V = ^-7t(2a)3 = -^7ta3 3	3
Mặt phảng (Oxy) đi qua gốc tọa độ o là tâm của (S) nên cắt (S) theo một đường tròn (C) là đường tròn lớn của (S). Do đó (C) có tâm là 0(0; 0; 0) và có bán kính là r = R = 2a.
Diện tích của khối trụ tương ứng:
Sxq = 27t.2a.aV3 = 4V3 7ta2
Thể tích của khối trụ tương ứng:
Vt = 7t.(2a)2.aV3 =4'/3na3
Bài 7. Trong không gian Oxyz cho hai đường thẳng di và d2 có phương trình:
dx:
X = 2t'
• y = -1 +1'
z = t'
X = 1 - t
• y = t và d2: z = -t
Chứng minh rằng hai đường thẳng di và d2 chéo nhau.
Viết phương trình mặt phẳng (a) chứa di và song song với d2.
Giải
a) Đường thẳng di đi qua điểm M(l; 0; 0) và có vectơ chỉ phương ũ = (-1; 1; -1).
Đường thẳng d2 đi qua điểm N(0; -1; 0) và có vectơ chỉ phương V = (2; 1; 1)7
Suy ra ũ và V không cùng phương.
ì - t = 2t'
Ta xét hệ phương trình:
Dễ thấy hệ phương trình trên là vô nghiệm.
Vậy hai đường thẳng di và d2 chéo nhau.
b)_Mặt phẳng (a) chứa di và song song với d2 nên M(l; 0; 0) e (a) và (a) có vectơ pháp tuyến là n = ũ A V = (2; -1; -3).
Phương trình của mặt phẳng (ct) là:
2.(x - 1) - l.(y - 0) - 3.(z - 0) = 0 2x-y-3z-2 = 0
Bài 8. Trong không gian Oxyz cho các điểm:
A(l; 0; -1), B(3; 4; -2), C(4; -1; 1), D(3; 0; 3).
Chứng minh rằng A, B, c, D không đồng phẳng
Viết phương trình mặt phẳng (ABC) và tính khoảng cách từ D đến (ABC).
Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD.
Tính thể tích tứ diện ABCD.
Giải
Ta có AB = (2; 4; -1), Ãc = (3; -1; 2), ÃD = (2; 0; 4) Giả sử ba vectơ AB, AC, AD đồng phẳng.
Khi đó tồn tại cặp số (m; n) sao cho
AB - mAC + nAD
2 = 2m + 2n • 4 = -m -1 = 2m + 4n
Dễ thấy hệ phương trình trên vô nghiệm, vô lí. Do đó ba vectơ AB, AC, AD không đồng phẳng.
Vậy bốn điểm A, B, c, D không đồng phẳng.
Mặt phẳng (ABC) qua điểm A(l; 0; -1) và có vectơ pháp tuyến là:
AB A AC = (7; —7; —14), vectơ này cùng phương với vectơ ĩi = (1; -1; -2)
Phương trình của mặt phẳng (ABC) l.(x - 1) — l.(y — 0) — 2(z + 1) = 0
x-y-2z-3 = 0
Khoảng cách từ D đến mặt phẳng (ABC):
13-0-2.3-31 r- d(D, (ABC)) =	'	'	= V6
Vl2 + (-1)2 + (-2)2
Nhận thấy rằng AB.AC = 0 và AB.AD = 0 nên AB 1 AC và AB 1 AD
Mặt khác AC = (3; -1; 2), DC = (1; -1; 2) nên AC.DC = 0 => AC 1 DC
Ta dễ dàng chứng minh được CD ± BC.
Từ các kết quả trên ta suy ra được mặt cầu (S) ngoại tiếp tứ diện ABCD có đường kính là BD.
Tâm I của (S) là trung điểm của BD => 1(3; 2; ỉ)
2
Bán kính của (S):
R = ịBD = ịVo2 + (-4)2+52 = ịvĩĩ
2 2 v ' 2
Phương trình của mặt cầu (S):
41
(x - 3)2 + (y - 2)2 +
d) Gọi V là thể tích của khôi tứ diện ABCD, ta có: ,.AB
AC = Vũ, CD = Vẽ
V = ỉs	
T 2 ư(ACD)’
Z--1 =
=• S,4CD)=iVŨ.VĨ6=72Ĩ,AB= 7ỈĨ
Vậy V = Ì.V2Ĩ.V2Ĩ = 7 (đvtt).
3
Bài 9. Trong không gian Oxyz cho bốn điểm:
A(2; 4; -1), B(l; 4; -1), C(2; 4; 3), D(2; 2; -1).
Chứng minh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một. Tính thể tích khối tứ diện ABCD.
Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, c, D.
Viết phương trình mặt phẳng (a) tiếp xúc với mặt cầu (S) và song song với mặt phẳng (ABD).
Giải
Ta có ÃB = (-1; 0; 0), AC = (0; 0; 4), ÃD = (0; -2; 0).
Suy ra ÃB.ÃC = 0, ÃC.ÃD = 0, Ãẽ.ÃD = 0
Vậy AB, AC, AD vuông góc với nhau từng đôi một.
Thể tích khối tứ diện ABCD là:
V = 4aB.AC.AD = ị. 1.4.2 = ị (đvtt)
6	6	3
Phương trình của mặt cầu (S) có dạng:
X2 + y2 + z2 + 2ax + 2by + 2xz + d = 0 Do (S) đi qua bốn điểm A, B, c, D nên ta có hệ phương trình:
21 + 4a + 8b - 2c + d = 0 18 + 2a + 8b - 2c + d = 0 29 + 4a + 8b + 6c + d = 0 9 + 4a + 4b - 2c + d = 0
Giải được: a = - ậ, b = -3, c = -2, d = 7.
2
Vậy phương trình của mặt cầu (S) là:
X2 + y2 + z2 - 3x - 6y - 2z + 7 = 0
Mặt phẳng (ABD) có vectơ pháp tuyến là n = AB A AD = (0; 0; 2), n cùng phương với vectơ k = (0; 0; 1).
Do đó phương trình của mặt phẳng (a) có dạng: z + D = 0.
Mặt cầu (S) có tâm I
; 3; 1 I, bán kính R =	.
2
Mặt phẳng (a) tiếp xúc với (S) khi và chỉ khi: d(I, (a)) = R o 11 + D I =
•t> D = -1 +
hoặc
D =-1 -
Vậy phương trình của mặt phẳng (a) là:
1	.	^21	nt--*-- T <21 _n
X = 1 - 2t y = 2 + t và mặt z = 3 -1
z - 1 +	= 0 hoặc z - 1	— = 0
Bài 10. Trong không gian Oxyz cho đường thẳng d:
phảng (a): 2x + y + z = 0.
Tìm tọa độ giao điểm A của d và (a).
Viết phương trình mặt phẳng (p) qua A và vuông góc với d.
Giải
a) Tọa độ giao điểm của đường thẳng d và mặt phảng (a) ứng với t nghiệm đúng phương trình:
2(1 - 2t) + (2 + t) + (3 - t) = 0 o t = -Ị
Thế t = 4 vào phương trình của d ta được giao điểm của d và 4
(a) là điểm aÍ-^; Ệ
b) Đường thẳng d có vectơ chĩ phương ũ = (-2; 1; -1). Mặt phẳng (p) qua A và vuông góc với d nên (p) nhận ũ làm vectơ pháp tuyến, do đó phương trình của (p) là:
(	5>
(	15>
( 5Ì
X + —
+1.
y —
-1.
z - —
l 2j
4
 4x - 2y + 2z + 15 = 0 Bài 11. Trong không gian Oxyz cho các điểm:
A(—1; 2; 0), B(-3; 0; 2), C(l; 2; 3), D(0; 3; -2).
Viết phương trình mặt phẳng (ABC) và phương trình tham số của đường thẳng AD.
Viết phương trình mặt phẳng (a) chứa AD và song song với BC.
Giải
* AB = (-2; -2; 2), AC = (2; 0; 3). Vectơ pháp tuyến của mặt phẳng (ABC):
AB A AC = (-6; 10; 4), vectơ này cùng phương với vecto' h = (3; -5; -2).
Phương trình của mặt phăng (ABC):
3(x + 1) - 5(y - 2) - 2(z - 0) = 0 3x — 5y - 2z + 13 = 0
X = -1 + t • y = 2 + t
z = -2t
* Đường thẳng AD có vectơ chỉ phương ũ = AD = (1; 1; -2).
Phương trình tham số của đường thẳng AD là:
Mặt phẳng (a) chứa AD và song song với BC nên điểm A(-l; 2; 0) e (a) và (a) có vectơ pháp tuyến là n = AD A BC.
AD = (1; 1; -2), BC = (4; 2; 1) => n = (5; -9; -2)
Phương trình của mặt phẳng (BCD):
5(x + 1) - 9(y - 2) - 2(z - 0) = 0 5x - 9y - 2z + 23 = 0
Bài 12. Trong không gian Oxyz cho bốn điểm:
A(3; -2; -2), B(3; 2; 0), C(0; 2; 1) và D(-l; 1; 2)
Viết phương trình mặt phảng (BCD). Suy ra ABCD là một tứ diện.
Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (BCD).
Tìm tọa độ tiếp điểm của (S) và mặt phẳng (BCD).
Giải
a) Mặt phẳng (BCD) có vectơ pháp tuyến n = BC A BD.
BC = (-3; 0; 1), BD = (-4; -1; 2)
=> n =(1; 2; 3)
Phương trình của mặt phẳng (BCD):
l(x - 3) + 2(y - 2) + 3(z - 0) = 0
x + 2y + 3z-7 = 0 (*)
Thế tọa độ điểm A vào phương trình (*) ta thấy phương trình không nghiệm đúng, nên A g (BCD).
Vậy ABCD là một tứ diện.
b) Gọi (cc) là mặt phẵng (BCD). Mặt cầu (S) tâm A tiếp xúc với (ct) nên có bán kính là:
R = d(A, (a)) =
3 + 2(-2) + 3(-2) - 7
Vl2 + 22 + 32
Phương trình của mặt cầu (S) là:
(x - 3)2 + (y + 2)2 + (z + 2)2 = 14
Gọi H là tiếp điểm của (S) và (a) thì H là hình chiếu vuông góc của A trên (a). Nếu gọi A là đường thẳng đi qua A và vuông góc với (a) thì H là giao điểm của A và (a).
Đường thẳng A có vectơ chỉ phương là ũ = h =(1; 2; 3).
X = 3 + t
Phương trình tham sô’ của A: < y = -2 + 2t z = -2 + 3t
Tọa độ của H ứng với t nghiệm đúng phương trình: (3 + t) + 2(-2 + 2t) + 3(-2 + 3t) - 7 = 0
« t = 1
Suy ra tiếp điểm của (S) và (a) là điểm H(4; 0; 1). Bài 13. Trong không gian Oxyz, cho hai đường thẳng:
X = t y = 1 + t z = -3 + 2t
X = -1 + 3t y - 1 + 2t và d2 z = 3 - 2t
Chứng minh di và d2 cùng thuộc một mặt phẳng.
Viết phương trình mặt phảng đó.
Giải
a) Đường thẳng di đi qua điểm M(-l; 1; 3) và có vectơ chỉ phương ũ = (3; 2; -2).
Đường thẳng d2 đi qua điểm N(0; 1; 3) và có vectơ chỉ phương V = (1; 1; 2)7
Nhận thấy hai vectơ ũ và V không cùng phương. Ta xét hệ phương trình:
3t -1' = 1 2t -1' = 0 t + t' = 3
-1 + 3t = t'
1 + 2t = 1 + t' <i 3 - 2t = -3 + 2t'
Giải hệ ta được: t = 1; t' = 2.
Suy ra hai đường thẳng di và d2 cùng thuộc một mặt phảng.
b) Gọi (ct) là mặt phẳng chứa di và d2 thì điểm M(-l; 1; 3) e (a) có vectơ pháp tuyến là:
n = ũ A V = (6; -8; 1)
Phương trình của mặt phẳng (a) là:
(x + 1) - 8(y - 1) + l.(z - 3) = 0 6x-8y + z + ll
Bài 14. Trong không gian cho ba điểm A, B, c.
Xác định điểm G sao cho GA + 2GB - 2GC = õ
Tìm tập hợp các điểm M sao cho MA2 + 2MB2 - 2MC2 = k2, với k là hằng số.
Giải
GA + 2GB - 2GC = ỗ o GA = -2GB « ÃG = 2CB
Vậy điểm G được xác định bằng hệ thức vectơ AG = 2CB .
Ta có:
MA2 + + 2MB2 - 2MC2 = k2 » (ÕẤ - GM)2 + 2(g§ - GM)2 - 2(GC - Gm)2 = k2
o GM2 + GA2 + 2GB2 - 2GC2 - 2 GM.(GA + 2GB - 2GC) = k2
 GM2 + GA2 + 2GB2 - 2GC2 = k2 (vì GA + 2GB - 2GC = 0 )
» GM2 = k2 - (GA2 + 2GB2 - 2GC2)
Biện luận:
Nếu k2 < GA2 + 2GB2 - 2GC2 thì tập hợp các điểm M là tập 0.
Nếu k2 = GA2 + 2GB2 - 2GC2 thì GM = 0 M = G.
Vậy tập hợp các điểm M là tập {GỊ.
Nếu k2 > GA2 + 2GB2 - 2GC2
thì k2 - (GA2 + 2GB2 - 2GC2) > 0, ta được:
GM = ựk2 - (GA2 + 2GB2 - 2GC2) (hằng số) Vậy tập hợp các điểm M là mặt cầu tâm G bán kính
R = ựk2 - (GA2 + 2GB2 - 2GC2)
X = 2 + 2t < y = t
z = 1 + t
Bài 15. Cho hai đường chéo nhau
d:
X = 2 -1
■ y = -1 + t và d' z = 1 -1
Viết phương trình các mặt phẳng (oc) và (p) song song với nhau và lần lượt chứa d và d'.
Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng (P) và khoảng cách từ M' đến mặt phẳng (a). So sánh hai khoảng cách đó.
Giải
a) Đường thẳng d đi qua điểm M(2; -1; 1) và có vectơ chỉ phương ũ = (-l; 1;-1).
Đường thẳng d' đi qua điểm M'(2; 0; 1) và có vectơ chỉ phương V = (2; 1; 1).
Từ giả thiết suy ra M G (a), M' <= (p) và hai mặt phẳng này cùng có vectơ pháp tuyến.
n = ũ A V = (2; -1; -3)
Phương trình của mặt phắng (a):
2.(x - 2) - l.(y + 1) - 3(z - 1) = 0
 2x - y - 3z - 2 = 0 Phương trình của mặt phẳng (P):
2.(x - 2) - l.(y - 0) - 3(z - 1) = 0
2x-y-3z-l = 0
b) * Khoảng cách từ M(2; -2; 1) đến mặt phẳng (p):
d(M, (P)) =
2.2 -(!-)- 3(1) -1
V22 + (l2) + (-3)2
1
* Khoảng cách từ M'(2; 0; 1) đến mặt phẳng (a):
d(M', (a)) =
|2.2 - 0 - 3.(1) - 2| V22 + (l2) + (-3)2
Vậy d(M, (p)) = d(M', (a)) =
V14
Bài 16. Trong không gian Oxyz cho:
mặt phẳng (a) có phương trình 4x + y + 2z + l = 0
và mặt phẳng (P) có phương trình 2x-2y + z + 3 = 0
Chứng minh rằng (a) cắt (p).
Viết phương trình tham số của đường thẳng d là giao của (a) và (p).
Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (a).
Tìm điểm N' là ảnh của N(0; 2; 4) qua phép đối xứng qua đường thẳng d.
Giải
a) Mặt phẳng (a) có vectơ pháp tuyến na = (4; 1; 2).
Mặt phẳng (P) có vectơ pháp tuyến rip = (2; -2; 1)
Ta có: n .n = 4.2 + l.(-2) + 2.1 = 8^0 Vậy hai mặt phẳng (a) và (p) cắt nhau.
nghiệm đúng hệ phương trình:
2x-2y + z + 3 = 0
Cho X = 0 ta được:
y + 2z + 1 = 0
<_	_	_ o
2y + z + 3 = 0
Suy ra điểm A(0; 1; -1) e d.
Đường thẳng d có vectơ chỉ phương là:
ã = nu A np = (5; 0; -10), ã cùng phương với vectơ b = (1; 0; -2)
Phương trình tham số của d là:
X = t
• y = 1 z = -1 - 2t
c) Qua điểm M(4; 2; 1) ta dựng đường thẳng A vuông góc với mặt phảng (a) tại điểm H. Vì M' là điểm đốì xứng của M qua (a) nên H là trung điểm của đoạn thẳng MM'.
Đường thẳng A nhận fiu = (4; 1; 2) làm vectơ chỉ phương, do đó
A có phương trình tham số là:
X = 4 + 4t - y = 2 + t (*)
z = 1 + 2t
Tọa độ điểm H ứng với t nghiệm đúng phương trình:
4(4 + 4t) + (2 + t) + 2(t + 2t) + 1 = 0 t = -1
Thế t = -1 vào (*) ta được H(0; 1; -1).
Gọi M'(x'; y'; z') ta có:
x' = 2xh - XM = 0 - 4 = -4
•y' = 2y„-y" =2-2 = 0 z' = 2zH - 2zm = -2 - 1 = -3
Vậy M'(-4; 0; -3).
d) Qua điểm N(0; 2; 4) ta dựng mặt phẳng (P) vuông góc với d tại điểm K. Vì N' là điểm đối xứng của N qua d nên K là trung điểm của đoạn thẳng NN'.
b) Vì d là giao tuyến của (a) và (p) nên d là tập hợp các điểm (x; y; z) 4x + y + 2z + l = 0
Mặt phẩng (P) vuông góc với d nên nhận vectơ b = (1; 0; 2) làm vectơ pháp tuyến.
Phương trình của mặt phẳng (P) là:
l.(x - 0) - 2.(z -4) = 0x-2z + 8 = 0
Tọa độ của K nghiệm đúng hệ phương trình:
X = t
• y = 1	(1)
z = —1 — 2t
X - 2z + 8 = 0	(2)
Thế (1) vào (2) ta được:
t - 2(-1 - 2t) + 8 = 0 t = -2
Thế t = -2 vào (1) ta được K(-2; 1; 3).
Gọi N(x0; y0; z0) ta có:
x() =2xK -XN = -4-0 = -4 yo=2yK-yN=2-2 = O z0 - 2zK - ZN = 6 - 4 = 2
Vậy N'(-4; 0; 2).