SGK Hình Học 10 - Bài 1. Phương trình đường thẳng - Câu hỏi và bài tập
vectơ AB. CHƯƠNG
PHƯƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHANG
♦í* Phương trình đường thẳng
♦í* Phương trình đường tròn
Trong chương này chúng ta sử dụng phương pháp toạ độ để tìm hiểu về đường thẳng, đường tròn và đường elip.
Hình 3.1
*í* Phương trình đường elip
§1. PHƯƠNG TRÌNH ĐƯỜNG THANG
Vectơ chỉ phương của đưòng thẳng
Tìm tung độ của hai điểm Mg và M nằm trên A, có hoành độ lần lượt là 2 và 6.
Cho vectơ U = (2; 1). Hãy chứng tỏ MQM cùng phương với U.
A
Hình 3.2
Định nghĩa
Vectơ u được gọi là vectơ chỉ phương của đường thẳng ĩs nếu M õ và giá của U song song hoặc trùng với A.
Nhận xét
Nếu u là một vectơ chỉ phưorng của đường thẳng A thì ku (k* 0) cũng là một vectơ chỉ phương của A. Do đó một đường thẳng có vô số vectơ chỉ phương.
Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương của đường thẳng đó.
Phưong trình tham số của đưòng thảng
Định nghĩa
Trong mặt phảng Oxy cho đường thẳng A đi qua điểm Mữ(xữ ; >’o) và nhận H = («j ; m2) làm vectơ chỉ phương. Với mỗi điểm M(x ; ỳ) bất kì trong mặt phẳng, ta có MQM - (% - x0; y - y0). Khi đó
MqM - tu
5
X - X - tu ì
y-y«=,uĩ
X = XQ + iz/j
y=j0+ÍM2
(1)
Hệ phương, trình (1) được gọi là phương trình tham số của đường thẳng A, trong đó t là tham số.
^.2
Cho t một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng A.
Hãy tìm một điểm có toạ độ xác định và một vectơ chỉ phương của đường thẳng có phương trình tham số
X - 5-6t y = 2 + 8t.
Liên hệ giữa vectơ chỉ phương và hệ sô góc của đường thẳng Cho đường thẳng A có phương trình tham số
X = XQ + y = }'o+%-
Nếu M] 0 thì từ phương trình tham số của A ta có
'í=ỉz3>
< Mj
/-?0=ft<2
suy ra y-y0= ^-(x-x0).
Uị
1 u
Đặt k = — ta .được y-y0 = k(x - x0).
Gọi A là giao điểm của A với trục hoành, Âv là tia thuộc A ở về nửa mặt phẳng toạ độ phía trên (chứa tia Oy). Đặt ữ- xAv, ta thấy k = tana Số k chính là hệ số góc của đường thẳng A mà ta đã biết ở lớp 9.
Như vậy nếu đường thẳng A có vectơ chỉ phương u - (uị ; w2) với Wj 0 thì A có hệ số góc k = —■
Tính hệ số góc của đường thẳng d có vectơ chỉ phương là U - (-1; 73).
Ví dụ. Viết phương trình tham số của đường thẳng d đi qua hai điểm Â(2 ; 3) và 5(3 ; 1). Tính hệ số góc của d.
GIẢI
Vì d đi qua A và B nên d có vectơ chỉ phương AB = (1 ; -2).
X = 2 +1 y = 3-2t.
Hệ số góc của d là k =
U1
1
Phương trình tham số của d là
^4 Cho đường thẳng A có phương trình ■
X = -5 + 2t
và vectơ n = (3 ; -2). Hãy
Vectơ pháp tuyến của đưòng thẳng
[y = 4 + 3f
chứng tỏ n vuông góc với vectơ chỉ phương của A.
Định nghĩa
Vectơ n được gọi là vectơ pháp tuyển của đường thẳng A nếu n 0 và n vuông góc với vectơ chỉ phương của A.
Nhận xét
Nếu n là một vectơ pháp tuyến của đường thẳng A thì kn (k / 0) cũng là một vectơ pháp tuyến của A. Do đó một đường thẳng có vô số vectơ pháp tuyến.
Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ pháp tuyến của nó.
4.
Phương trình tổng quát của đưòng thẳng
Trong mặt phẳng toạ độ Oxy cho đường thẳng A đi qua điểm Mq(Xq ; y0) và nhận «(«;/?) làm vectơ pháp tuyến.
Với mỗi điểm M(x ; y) bất kì thuộc mặt phẳng, ta có : MQM = (% - xữ; y - y0).
a(x - x0) + b(y - y0) = 0 ax + by + (-ứ%0 - ồy0) = 0 ax + by + c = 0
Khi đó : M(x ; y) G A « _L MqM
với c = -axQ - byữ.
Định nghĩa
II Phương trình ax + by + c = 0 với a và h không đồng thời bằng 0, II được gọi là phương trình tổng quát của đường thẳng.
Nhận xét. Nếu đường thẳng A có phương trình là ax + by + c = 0 thì A có vectơ pháp tuyến là n = (ữ ; b) và có vectơ chỉ phương là u = (-b ; a).
^5 Hãy chứng minh nhận xét trên.
Ví dụ. Lập phương trình tổng quát của đường thẳng A đi qua hai điểm A(2 ; 2) và B(4,3).
GIẢI
Đường thẳng A đi qua hai điểm A, B nên có vectơ chỉ phương là AB = (2; 1).
Từ đó suy ra A có vectơ pháp tuyến là n = (-1 ; 2). Vậy đường thẳng A có phương trình tổng quát là :
(-l).(x —2) + 2(y - 2) = 0 hay X - 2y + 2 = 0.
^6 Hãy tìm toạ độ của vectơ chỉ phương của đường thẳng có phương trình :
3x + 4y + 5 = 0.
Các trường hợp đặc biệt
Hình 3.6
Cho đường thẳng A có phương trình tổng quát ax + by + c - 0 (1)
• Nếu a — 0 phương trình (1) trở thành
c
ốy + c = 0hayy = -Ỵ--
Khi đó đường thẳng A vuông góc với
trục Oy tại điểm 0 ; -y (h.3.6).
I b)
XT-- 7 /XI , c
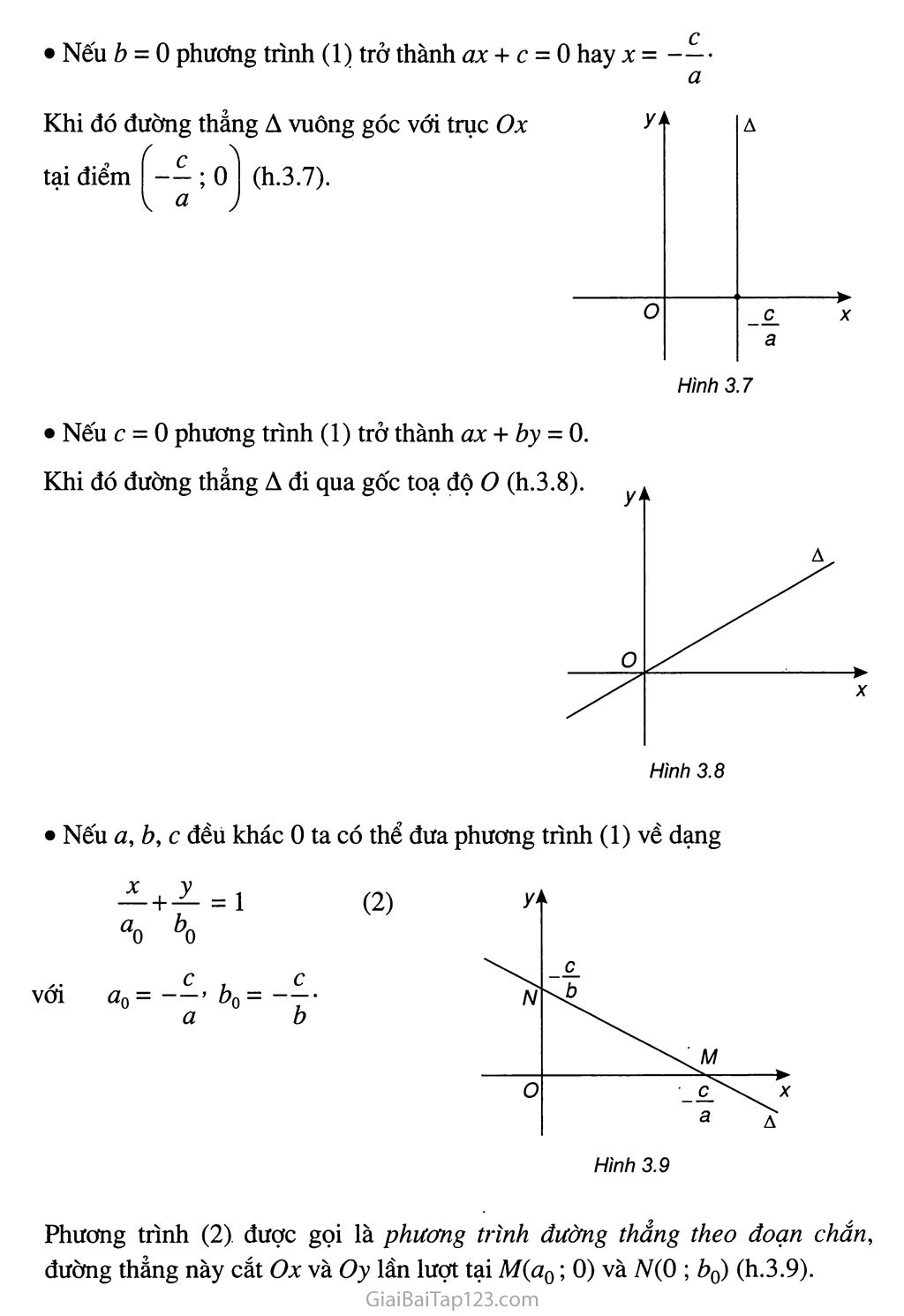
• Neu b = 0 phương trình (1) trở thành ax + c = 0 hay X = •
a
Khi đó đường thẳng A vuông góc với trục Ox tại điểm ; 0^ (h.3.7).
y-
A
o
c
X
a
Hình 3.7
A 7 Trong mặt phẳng Oxy, hãy vẽ các đường thẳng có phương trình sau đây: Ơ1: X - 2y = 0; d2: X = 2; ơ3:y+1 = 0;
Vị trí tương đối của hai đưòng thẳng
Xét hai đường thẳng At và A2 có phương trình tổng quát lần lượt là aỵx + bỵy + Cj = 0 và a^í + b2y + c2 - 0.
Toạ độ giao điểm của At và A, là nghiệm của hệ phương trình : a.x + b.y + c. =0 a^x + b^y + c =0.
Ta có các trường hợp sau :
Hệ (I) có một nghiệm (x0; y0), khi đó Aj cắt A2 tại điểm Mq(x0 ; y0).
Hệ (I) có vô số nghiệm, khi đó Aj trùng với A2.
Hệ (I) vô nghiệm, khi đó Aj và A2 không có điểm chung, hay Aj song song với A7.
Ví dụ. Cho đường thẳng d có phương trình X - y + 1 = 0, xét vị trí tương đối của d với mỗi đường thẳng sau :
Aj : 2x + y - 4 = 0 ; A2 : X - y - 1 = 0 ; A3 : 2x -2y + 2 = 0.
GIAI
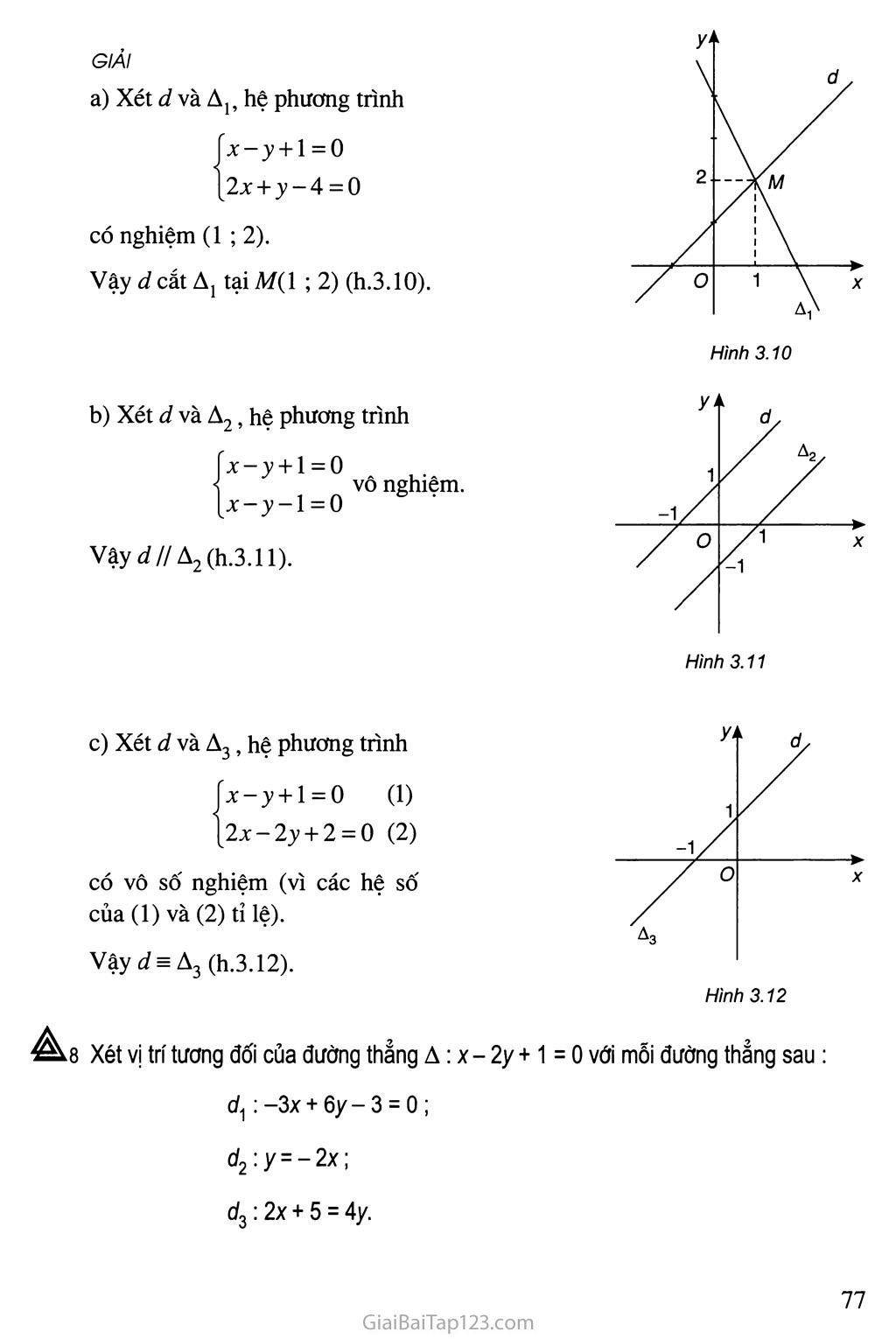
Xét d và A J, hệ phương trình
X - y +1 = 0 2x + y-4 = 0
có nghiệm (1 ; 2).
Vậy d cắt Aị tại A/(l ; 2) (h.3.10).
Xét d và A2, hệ phương trình
%-y+l=0
S vô nghiêm
[x-ỵ-l = o
Xét d và A3, hệ phương trình
%-y+l=0 (1)
2x-2y + 2 = 0 (2)
có vô số nghiệm (vì các hệ số của (1) và (2) tỉ lệ).
Vậyí/ = A3 (h.3.12).
^8 Xét vị trí tương đối của đường thẳng A:
Ơ1 : -3x + 6y - 3 = 0 ; đ2:y=-2x; ở3: 2x + 5 = 4y.
- 2y + 1 = 0 với mỗi đường thẳng sau :
Vậy í///A2 (h.3.11).
Góc giữa hai đưòng thẳng
^9 Cho hình chữ nhật ABCD có tâm I và các cạnh AB = 1, AD = 73. Tính số đo các góc AID và DIC.
Hai đường thẳng Aj và A, cắt nhau tạo thành bốn góc. Nếu Aj không vuông góc với A2 thì góc nhọn trong số bốn góc đó được gọi là góc giữa hai đường thẳng Aj và Aj. Nếu Aj vuông góc vói A2 thì ta nói góc giữa Aj và A2 bằng 90°. Trường hợp Aj và A2 song song hoặc trùng nhau thì ta quy ước góc giữa Aj và A2 bằng 0°. Như vậy góc giữa hai đường thẳng luôn bé hơn họặc bằng 90°.
Góc giữa hai đường thẳng Aj và A2 được kí hiệu là (Aj, A2) hoặc (Ap A^.
Cho hai đường thẳng
Aj : aỵx + bỵy + Cj = 0,
A2 : a^t + byy + = 0.
Đặt cp= (Aj, A7j thì ta thấy ộ? bằng hoặc bù với góc giữa nỵ và «2 trong đó
, «2 lần lượt là vectơ pháp tuyến của Aj và A2. Vì COS ộ? > 0 nên ta suy ra
Vậy
KF Chú ý
Aj 1 À, ± n ứl(32 + bfil = 0.
Nếu Aj và A2 có phương trình y = kpc + mxNa.y = k^x + m2 thì
Aj ± A2 kỵ.k2 = -1.
7.
Công thức tính khoảng cách từ một điểm đến một đưòng thẳng
Trong mặt phẳng Oxy cho đường thẳng A có phương trình ax + by + c = 0 và điểm Mq (xq ; y0)- Khoảng cách từ điểm Mq đến đường thẳng A, kí hiệu là cI(Mq, A), được tính bởi công thức
CHỨNG MINH
Phương trình tham số của đường thẳng m đi qua Mq(xq ; y0) và vuông góc với đường thẳng A là :
x = XQ +ta y = y0+tb
trong đó «(ứ ; ố) là vectơ pháp tuyến của A.
Giao điểm H của đường thẳng m và A ứng với giá trị của tham số là nghiệm tH của phương trình :
a (x0 + tà) + b{yữ + tb) + c = ồ.
Ta có
axữ+byữ+c
2 , k2
a +b
Vậy điểm H = (x0 + tHa ; y0 + tHb).
Từ đó suy ra d( Mữ , A) = MqH = yj(xH - XQ )2 + (yH - y0 )2
|or0 + byo + c|
ựữ2 + ò2
Á 10 Tính khoảng cách từ các điểm M(-2 ; 1) và 0(0 ; 0) đến đường thẳng A có phương trình 3x-2y-1 =0.
Câu hỏi và bài tạp
Lập phương trình tham số của đường thẳng d trong mỗi trường hợp sau :
d đi qua điểm M(2 ; 1) và có vectơ chỉ phương u = (3 ; 4);
d đi qua điểm M(-2 ; 3) và có vectơ pháp tuyến là « = (5 ; 1).
Lập phương trình tổng quát của đường thẳng A trong mỗi trường hợp sau :
A đi qua AỈ(-5 ; -8) và có hệ số góc £ = -3 ;
A đi qua hai điểm Â(2 ; 1) và B(-4 ; 5).
3.
4.
5.
Cho tam giác ABC, biết Â(1 ; 4), 5(3 ; -1) và C(6 ; 2).
Lập phương trình tổng quát của các đường thẳng AB, BC và CA ;
Lập phương trình tổng quát của đường cao AH và trung tuyến AM.
Viết phương trình tổng quát của đường thẳng đi qua điểm M(4 ; 0) và điểm V(0; -1).
Xét vị trí tương đối của các cặp đường thẳng d\ và J2 sau đây
a) dị: Ax - lOy +1=0
và
b) dị: Ỉ2x - 6y + 10 = 0 và
í/2 : X + y + 2 = 0 ;
x = 5 + t
d2
c) dị : 8.r + lOy -12 = 0 và
d2
y -3 + 2t; X = -6 + 5t
y-6-4t.
6.
Cho đường thẳng d có phương trình tham số
X = 2 + 2t y = 3+t.
Tìm điểm M thuộc d và cách điểm Â(0 ; 1) một khoảng bằng 5.
Tim số đo của góc giữa hai đường thẳng và d2 lần lượt có phương trình
: AfX - 2y + 6 = 0 và í/2 : X - 3y + 1 = 0.
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau :
A(3;5), A : 4% + 3y + 1 = 0 ;
5(l;-2), c/: 3x - 4y - 26 = 0 ;
C(1 ; 2), m : 3x + 4y - 11 = 0.
Tim bán kính của đường tròn tâm C(-2 ; -2) tiếp xúc với đường thẳng A : 5x + 12y - 10 = 0.