SGK Hình Học 10 - Bài 3. Các hệ thức lượng trong tam giác và giải tam giác - Câu hỏi và bài tập

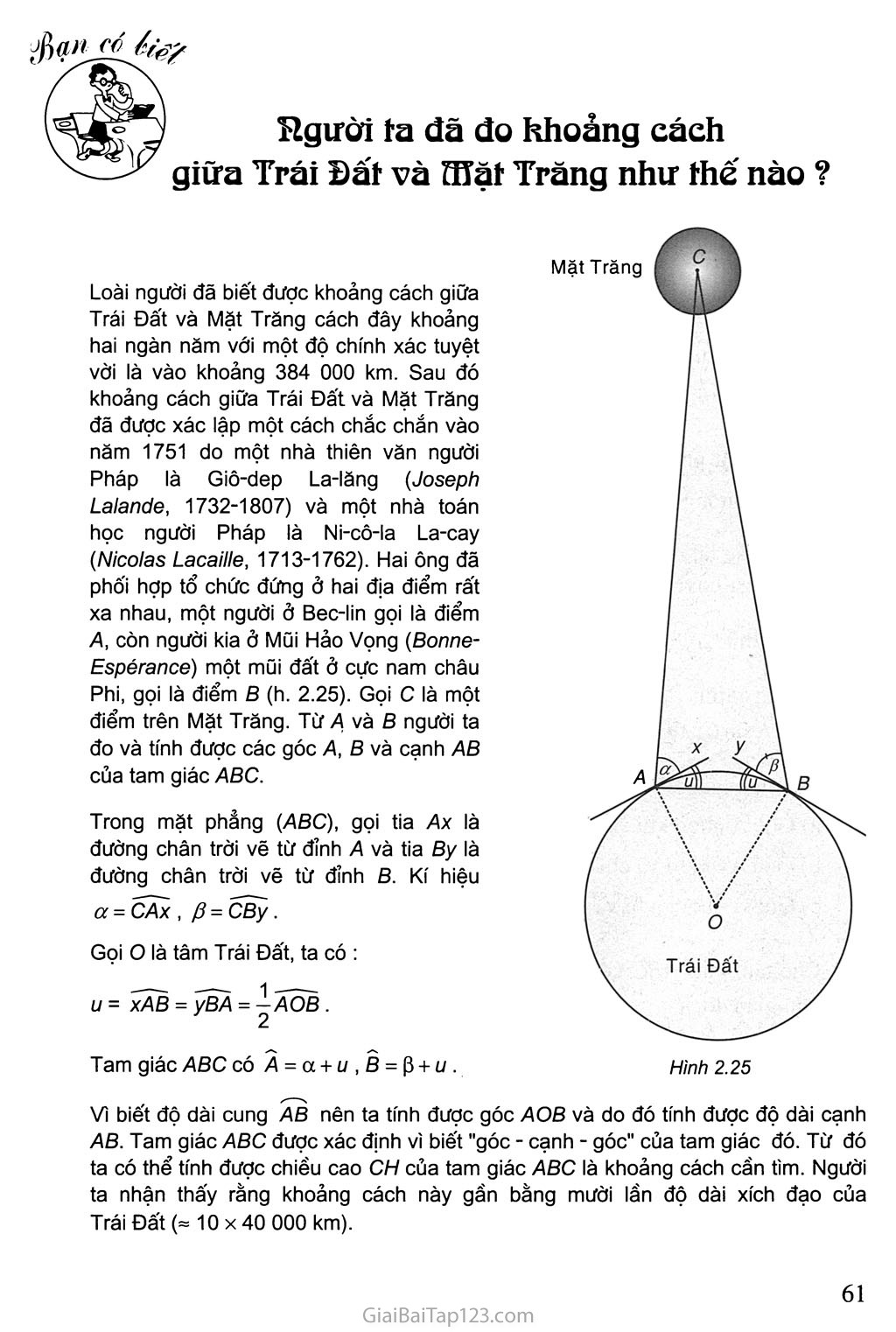
§3. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC
VÀ GIẢI TAM GIÁC
Chúng ta biết rằng một tam giác được hoàn toàn xác định nếu biết một số yếu tố, chẳng hạn biết ba cạnh, hoặc hai cạnh và góc xen giữa hai cạnh đó.
Như vậy giữa các cạnh và các góc của một tam giác có một mối liên hệ xác định nào đó mà ta sẽ gọi là các hệ thức lượng trong tam giác. Trong phần này chúng ta sẽ nghiên cứu những hệ thức đó và các ứng dụng của chúng.
Đối với tam giác ABC ta thường kí hiệu : a = BC, b = CA, c - AB.
^1 Tam giác ABC vuông tại 4 có đường cao AH= hvà có BC = a,CA = b, AB = c. Gọi BH = c'và CH = b' (h.2.11). Hãy điên vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông :
a2=b2+Q ò2 = ax □ c2 = ax □ h2=b'x □ ah = bx I ... I
sinfi = cosC = J=1; sinC = cosB =
a
tanB = cotc =
a
=Q;
cots = tanC =
.ạ
b
1 _ 1 1 □ %2+c2
Trước tiên ta tìm hiểu hai hệ thức lượng cơ bản trong tam giác bất kì là định lí côsin và định lí sin.
1.
Định lí côsin
a) Bài toán. Trong tam giác ABC cho biết hai cạnh AB, AC và góc A, hãy tính cạnh BC (hình 2.12).
GIẢI
Ta CÓ BC2 =\bc\2 =(aC-AB^2
= AC2 + ÃB2 -2ÃCÃB
BC- = AC2 +ĂB2 -2|ac|.|as|cos a .
Hình 2.12
Vậy ta có BC2 = AC2 + AB2 - 2AC.AB. COS A nên	BC = yjAC2 + AB2 - 2AC.AB. COS A .
Từ kết quả của bài toán trên ta suy ra định lí sau đây :
b) Định lí cô sin
Trong tam giác ABC bất kì với BC - a, CA - b, AB = c ta có :
a~ = b~ + c2 - 2bc cosA ; b2 - a2 + c2 - 2ac cosB ; c2 = a2 + b2 - 2ab cosC.
Hãy phát biểu định lí côsin bằng lời.
Khi ABC là tam giác vuông, định lí côsin trở thành định lí quen thuộc nào ? Từ định lí côsin ta suy ra :
Áp dụng. Tính độ dài đường trung tuyến của tam giác.
Cho tam giác ABC có các cạnh BC - a, CA = b và AB - c. Gọi ma , mb và mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và c của
Thật vậy, gọi M là trung điểm của cạnh BC, áp dụng định lí côsin vào tam giác AMB ta có :
/„^2 2 2	2.(^1	~ a „	2 . đ
nC-c + —	-2c.--.cosB - c +—	ac COS B.
a \2)	2	4
Vì cosB -
a2+c2-b2
2ac
nên ta suy ra :
2 _ ,2	ơ2+c2-fr2	2(Z?2+c2)-ữ2
m„ = cz + -	ac .	— - —	—	
4	2ac
Chứng minh tương tự ta có :
2	2(ứ2+c2)-ồ2
2_2(ứ2+ồ2)-c2 mc =	 —;	 •
Cho tam giác ABC có a = 7 cm, b = 8 cm và c = 6 cm. Hãy tính độ dài đường trung tuyến ma của tam giác ABC đã cho.
Ví dụ
Ví dụ 1. Cho tam giác ABC có các cạnh AC = 10 cm, BC = 16 cm và góc c = 110°. Tính cạnh AB và các góc A, B của tam giác đó.
GIẢI
Đặt BC - a, CA = b, AB = c. Theo định lí côsin ta có :
c2 = a2 + b2 - 2ab COS c
= 162+ 102 - 2.16.10.cosll0°
c2 « 465,44.
B
Vậy c ~ ạ/465,44 ~ 21,6 (cm).
Theo hệ quả định lí côsin ta có :
_ ,	b2+c2-a2	102+(21,6)2-162
cos A =	— «	
• = 0,7188.
Hình 2.15
2bc	2.10.(21,6)
Suy ra 44°2’, B = 180° -(A + C) « 25°58’.
Ví dụ 2. Hai lực /j và /2 cho trước cùng tác dụng lên một vật và tạo thành góc nhọn (/ị , /2 j = a • Hãy lập công thức tính cường độ của hợp lực 5 .
GIẢI
Đặt AB = /1, AD = /2 và vẽ hình bình hành A6CD (h.2.15).
Khi đó ÃC = ÃB + ÃD = X + X = 5- Vậy H = |ac| = |/ì +^2|.
Theo định lí côsin đối với tam giác ABC ta có AC2 = AB2 + BC2 - 2AB.BC. COS B, hay 0 = |yj| +|/2| -2|/1|.|/2|.cos(180°-a).
Do đó 0 =	+/22 + 2|/i|.|/2|-cosư •
Định lí sin
^5 Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b,AB = c. Chứng minh hệ thức :
a b c
= 27?.
sin4 sinfi sinC
Đối với tam giác ABC bất kì ta cũng có hệ thức trên. Hệ thức này được gọi là định lí sin trong tam giác.
a) Định lí sin
Trong tam giác ABC bất kì với BC = a, CA - b, AB = c và R là bán kính đường tròn ngoại tiếp, ta có :
sin A sin B sin c
CHỨNG MINH. Ta chứng minh hệ thức ----- = 2R. Xét hai trường hợp :
sin A
• Nếu góc A nhọn, ta vẽ đường kính BD của đường tròn ngoại tiếp tam giác ASC và khi đó vì tam giác BCD vuông tại c nên ta có BC - BD. sin D hay ữ = 27?.sinD (h.2.16a).
Ta có BAC = BDC vì đó là hai góc nội tiếp cùng chắn cung BC. Do đó
a = 2R. sin A hay a = 2R.
sinÂ
• Nếu góc A tù, ta cũng vẽ đường kính BD của đường tròn tâm o ngoại tiếp tam giác ABC (h.2.16b). Tứ giác ABDC nội tiếp đường tròn tâm o nên
D = 180° - A . Do đó sinD = sin( 180° - A ). Ta cũng có BC - BD. sin D hay a = BD. sin A.
Vậy a - 27? sin A hay a = 2R.
sinÂ
Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.
b) Ví dụ. Cho tam giác ABC có B = 20°, c = 31° và cạnh b = 210 cm. Tính A , các cạnh còn lại và bán kính R của đường tròn ngoại tiếp tam giác đó.
Hình 2.17
Ta CÓ A = 180°-(20°+31°), do đó A = 129° (h.2.17) a b
Mặt khác theo định lí sin ta có :	= ■■■- - = ; — = 2R
sin A sin B sin c
= 477,2 (cm).
_ bsin 2l0.sinl29° Từ (l) suy ra a - —7
sin 5	sin 20°
ósinC 2l0.sin3l°
=	•-316,2 (cm).
sinB sin 20°
(1)
n a 	477,2	z	x
R -	= ——-—— « 307,02 (cm).
2 sin A 2. sin 129°
Công thức tính diện tích tam giác
Ta kí hiệu ha, hb và hc là các đường cao của tam giác ABC lần lượt vẽ từ các đỉnh A, B, c và s là diện tích tam giác đó.
Á?
Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.
Cho tam giác ABC có các cạnh BC = a,CA = b, AB = c.
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác và
a+b+c	
p =	 là nứa chu vi của tam giác.
Diện tích s của tam giác ABC được tính theo một trong các công thức sau :
(1)
(2)
(3)
s = —absinC = 2-ờcsin A - 2-cưsin B :
2 2 2
47? s = pr;
s = -ự/?(/? - ỡ)(p - b)(p - c) (công thức Hê-rông).
Ta chứng minh công thức (1).
(4)
Do đó 5 = ẬữbsinC.
2
abc
4R
Các công thức s= -^bc sin A và 5 - ca sin B được chứng minh tương tự.
8 Dựa vào công thức (1) và định lí sin, hãy chứng minh s =
9 Chứng minh công thức s = pr (h.2.19).
Hình 2.19
Ta thừa nhận công thức Hê-rông.
Ví dụ 1. Tam giác ABC có các cạnh a = 13 m, b - 14 m và c = 15 m.
Tính diện tích tam giác ABC ;
Tính bán kính đường tròn nội tiếp và ngoại tiếp tam giác ABC.
GIẢI
Ta cóp -	(13 + 14 + 15) = 21. Theo công thức Hê-rông ta có :
5 = ạ/21(21-13)(21-14)(21-15) = 84 (m2).
s 84
Áp dụng công thức 5 = pr ta có r = — = -77 =4.
p 21
Từ công thức 5 =
Vậy đường tròn nội tiếp tam giác ABC có bán kính là r - 4 m. abc
n __ abc 13.14.15 _
Ta có	^=“77" =—777— = 8,125 (m).
45	336
Ví dụ 2. Tam giác ABC có cạnh a = 2V3 , cạnh b = 2 và c = 30°. Tính cạnh c, góc A và diện tích tam giác đó.
GIẢI
Theo định lí côsin ta có
c2 =ữ2 +b2 -2abcosC = 12 + 4-2.273.2.^7 =4.
2
Vậy c = 2 và tam giác ABC có AB = AC = 2. Ta suy ra B - c - 30°.
Do đó A = 120°.
Ta có s = acsinS = ~273.2 • 7 = 73 (đơn vị diện tích).
Giải tam giác và ứng dụng yào việc đo đạc
Giải tam giác
Giải tam giác là tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.
Hình 2.20. Giác kế dùng để ngắm và đo đạc
Muốn giải tam giác ta thường sử dụng các hệ thức đã được nêu lên trong định lí côsin, định lí sin và các công thức tính diện tích tam giác.
Ví dụ 1. Cho tam giác ABC biết cạnh a = 17,4 m, B = 44°30/ và c = 64°.
Tính góc A và các cạnh b, c.
GIẢI
Tacó Ằ = 180° -(Ồ + C)= 180° - (44°30’ + 64o) = 71°30’.
do đó
, ứsinB
z> = . -
sinẨ
ữSĨnC c = ———
sinÂ
17,4.0,7009
0,9483
12,9 (m),
17,4.0,8988
0,9483
16,5 (m).
Ví dụ 2. Cho tam giác ABC có cạnh a = 49,4 cm, b = 26,4 cm và c - 47°20’. Tính cạnh c, A và B .
GIẢI
Theo định lí côsin ta có
c2 = a2 +b2 - 2ab COS c
- (49,4)2 + (26,4)2 - 2.49,4.26,4.0,6777 = 1369,66. Vậy c - ựl369,66 ~ 37 (cm).
Ta có cos A =
z?2 + c2 -ữ2
2bc
697 + 1370-2440 = _0 2.26,4.37
Như vậy A là góc tù và ta có A ~ 101°.
Dođó B = 180° -(Â + C) = 180°-(101°+47°20') = 31°40'.
Vậy Ồ = 31°40'.
Ví dụ 3. Cho tam giác ABC có cạnh a = 24 cm, z? = 13 cm và c = 15 cm. Tính diện tích 5 của tam giác và bán kính r của đường tròn nội tiếp.
Theo định lí sin ta có a = —— = .c , sin sin B sinC
GIAI
Theo định lí côsin ta có như vậy A là góc tù và ta tính được A ~ 117°49’ => sinA ~ 0,88.
COSÂ =
b2+c2-a2
2bc
169 + 225-576
2.13.15
0,4667,
Ta có s = 4 bcsinA ~ 4.13.15.0,88 = 85,8 (cm2).
2 2
X	1 X	X	Ư
Ap dụng công thức s - pr ta có r = —. Vì p = p
24 + 13 + 15
2
= 26 nên
85,8
26
= 3,3 (cm).
ứng dụng vào việc đo đạc
Bài toán 1. Đo chiều cao của một cái tháp mà không thể đến được chân tháp. Giả sử CD = h là chiều cao của tháp trong đó c là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B và c thẳng hàng. Ta đo khoảng cách AS và các góc CAD, CBD. Chẳng hạn ta đo được AS = 24 m, CAD = a = 63°, CBD - (ỉ- 48°. Khi đó chiều cao h của tháp được tính như sau :
Hình 2.21
Áp dụng định lí sin vào tam giác ABD ta có AD _ AB sin /3 sin D
Tacó a = D + /3 nên D = a-/3 = 63°-48° = 15°
AS sin/? 24 sin 48°
Do đó AD = ,	„ = 68,91.
sin(ơ-/J) sin 15°
Trong tam giác vuông ACD ta có h - CD - ADsma =61,4 (m).
Bài toán 2. Tính khoảng cách từ một địa điểm trên bờ sông đến một gốc cây trên một cù lao ở giữa sông.
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây c trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm c. Ta đo khoảng cách AS, góc CAB và CBA. Chẳng hạn ta đo được A6 = 40 m, CAB = a = 45°, CBA = /? = 70°.
B
Hình 2.22
Khi đó khoảng cách AC được tính như sau : Áp dụng định lí sin vào tam giác ABC, ta có
-^- = -^1; (h.2.22). sin B sin c
• z-1	ZA XZ-. /15sinZ? 40.sin70°	..	,
Vi sinC = sin (or + /6) nên AC = ~ H	~ 41,47 (m).
sin(a+/7)	sin 115°
Vậy AC ~ 41,47 (m).
Câu hỏi và bài tạp
Cho tam giác ABC vuông tại A, B - 58° và cạnh a = 72 cm. Tính c, cạnh b, cạnh c và đường cao ha.
Cho tam giác ABC biết các cạnh a = 52,1 cm, b = 85 cm và c = 54 cm. Tính các góc A , B và c .
Cho tam giác ABC có A = 120°, cạnh b = 8 cm và c = 5 cm. Tính cạnh a, và các góc B, c của tam giác đó.
Tính diện tích s của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.
Tam giác ABC có Â = 120°. Tính cạnh BC cho biết cạnh AC - m và AB = n.
Tam giác ABC có các cạnh a = 8 cm, b = 10 cm và c = 13 cm.
Tam giác đó có góc tù không ?
Tính độ dài trung tuyến MA của tam giác ABC đó.
Tính góc lớn nhất của tam giác ABC biết
Các cạnh a = 3 cm, b = 4 cm và c - 6 cm ;
Các cạnh ữ = 40 cm, b - 13 cm và c = 37 cm.
Cho tam giác ABC biết cạnh a - 137,5 cm, B = 83° và c = 57° . Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.
Cho hình bình hành ABCD có AB = a, BC = b, BD = m và AC = n. Chứng
minh rằng	+ «2 = 2(ữ2 + h2).
Hai chiếc tàu thuỷ p và Q cách nhau 300 m. Từ p và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc BPA = 35° và BQA = 48°. Tính chiều cao của tháp.
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận (h.2.23), người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB - 12 m cùng thẳng hàng với chân c của tháp để đặt hai giác kế (h.2.24). Chân của giác kế có chiều cao h = 1,3 m. Gọi D là đỉnh tháp và hai điểm Âj,5j cùng thẳng hàng với Cị thuộc chiều cao Cữ của tháp. Người ta đo được DAịCị = 49° và DBịCị = 35°. Tính chiều cao CD của tháp đó.
Hình 2.23	Hình 2.24
ạ/ncổ/ẽé?
người tư đã đo khoảng cách
giữa Trái Đất và aĩặt Trăng như thế nào ?
Loài người đã biết được khoảng cách giữa Trái Đất và Mặt Trăng cách đây khoảng hai ngàn năm với một độ chính xác tuyệt vời là vào khoảng 384 000 km. Sau đó khoảng cách giữa Trái Đất và Mặt Trăng đã được xác lập một cách chắc chắn vào năm 1751 do một nhà thiên văn người Pháp là Giô-dep La-lăng (Joseph Lalande, 1732-1807) và một nhà toán học người Pháp là Ni-cô-la La-cay (Nicolas Lacaille, 1713-1762). Hai ông đã phối hợp tổ chức đứng ở hai địa điểm rất xa nhau, một người ở Bec-lin gọi là điểm A, còn người kia ở Mũi Hảo Vọng (Bonne- Espérance) một mũi đất ở cực nam châu Phi, gọi là điểm B (h. 2.25). Gọi c là một điểm trên Mặt Trăng. Từ A và B người ta đo và tính được các góc A, B và cạnh AB của tam giác ABC.
Trong mặt phẳng (ABC), gọi tia Ax là đường chân trời vẽ từ đỉnh A và tia By là đường chân trời vẽ từ đỉnh B. Kí hiệu a = CAx , /3 = CBy.
Gọi o là tâm Trái Đất, ta có :
u = xAB = yBA =	.
Tam giác ABC có 4 = a + u,B = p + ív.
Vì biết độ dài cung AB nên ta tính được góc AOB và do đó tính được độ dài cạnh AB. Tam giác ABC được xác định vì biết "góc - cạnh - góc" của tam giác đó. Từ đó ta có thể tính được chiểu cao CH của tam giác ABC là khoảng cách cần tìm. Người ta nhận thấy rằng khoảng cách này gần bằng mười lần độ dài xích đạo của Trái Đất (- 10 x40 000 km).