SGK Hình Học 10 - Bài 3. Tích của vectơ với một số - Câu hỏi và bài tâp

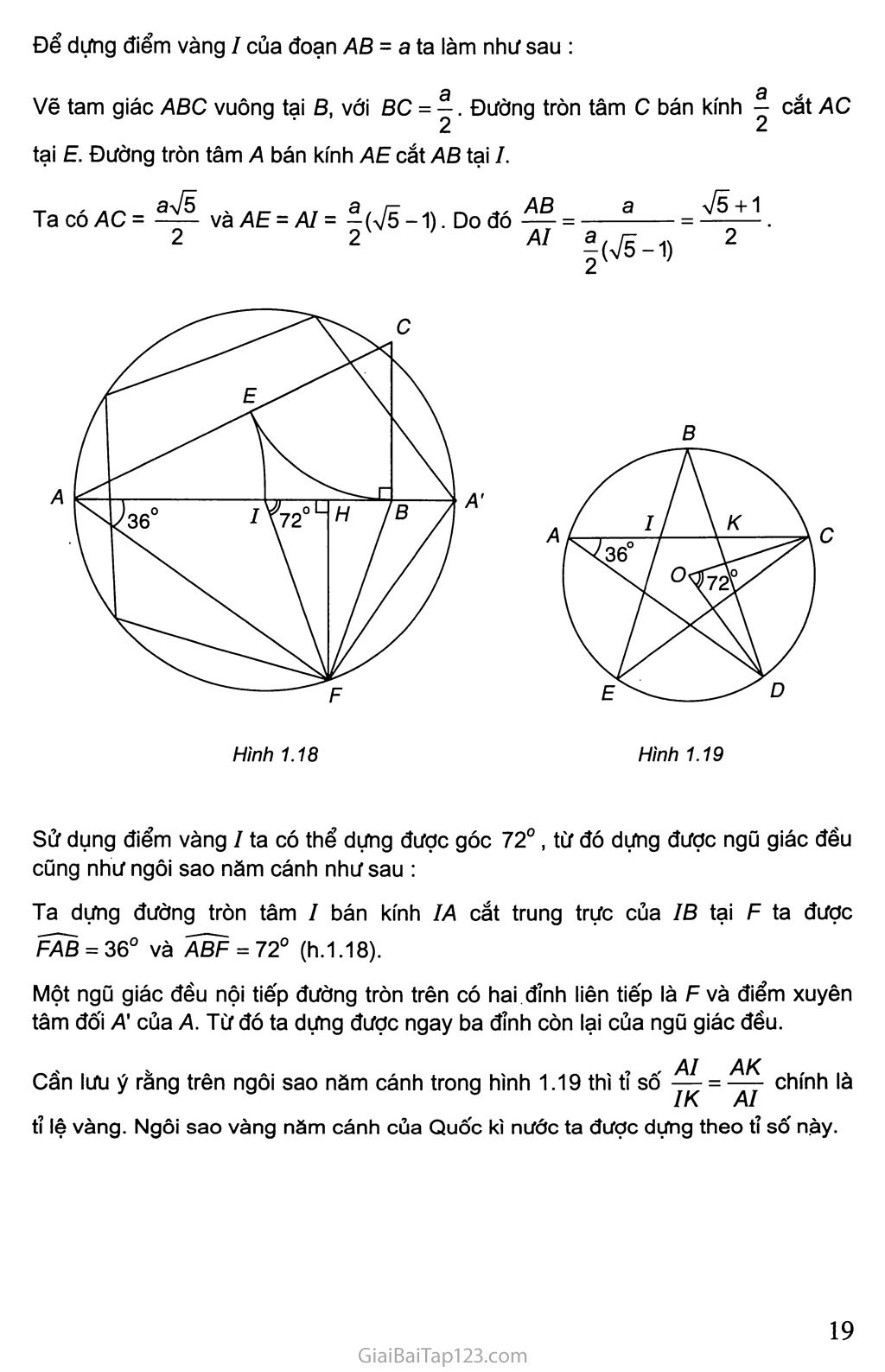
§3. TÍCH CỦA VECTƠ VỚI MỘT số
Định nghĩa
ị| Cho số k *0 và vectơ a * 0. Tích của vectơ a với số k là một vectơ, kí hiệu là ka , cùng hướng với a nếu k > 0, ngược
II hướng với a nếu k <0 và có độ dài hằng k’lU.
Ta quy ước Oa = 6 , k 6 = õ.
Người ta còn gọi tích của vectơ với một số là tích của một số với một vectơ.
Ví dụ 1. Cho G là trọng tâm của tam giác ABC, D và E lần lượt là trung điểm của5C và AC. Khi đó ta có (hl. 13)
Hình 1.13
GA = l~T)GD, AD = 3GD,
M4X
Tính chất
Với hai vectơ a và ĩ> bất kì, với mọi số h và k, ta có k(a + to = ka + kb ;
(h + k) a = ha + ka ;
h(ka3) = (hk)a ;
l.a = a, (-l).ứ = -a.
^2 Tìm vectơ đối của các vectơ ka và 3 a -40.
Trung điểm của đoạn thẳng và trọng tâm của tam giác
Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có MA + MB = 2M1.
Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có ~MA + MB + MC = 3MG.
^3 Hãy sử dụng mục 5 của §2 để chứng minh các khẳng định trên.
Điều kiện để hai vectơ cùng phương
Điều kiện cần và đủ để hai vectơ a và ĩ) (b*0) cùng phương là có một số kđể a -kb.
Thật vậy, nếu a = kb thì hai vectơ a và b cùng phương.
Ngược lại, giả sử ữ và ố cùng phương. Ta lấy k = -H nếu ữ và ố cùng
IốI
hướng và lấy k = -H nếu a và Z? ngược hướng. Khi đó ta có a = kb.
\b\
Nhận xét. Ba điểm phân biệt A, B, c thẳng hàng khi và chỉ khi có số k khác 0 để Ãè - kÃC.
5.
Phân tích một vectơ theo hai vecto không cùng phương
Cho a = OA,b = OB là hai vectơ không
cùng phương và X = oc là một vectơ tuỳ ý. Kẻ CA' II OB và CB’ II OA (h. 1.14). Khi đó X = ÕC = ÕA'+ OB'. Vì ÕA' và a là hai vectơ cùng phương nên có số h để OA' = ha. Vì OB' và b cùng phương nên có số k để OB' = kb.
Vậy x-ha + kb.
Khi đó ta nói vectơ X được phân tích (hay còn được gọi là biểu thị) theo hai vectơ không cùng phương a và b.
Một cách tổng quát người ta chứng minh được mệnh đề quan trọng sau đây :
Cho hai vectơ a và b không cùng phương. Khi đó mọi vectơ X đều phân tích được một cách duy nhất theo hai vectơ a và b, nghĩa là có duy nhất cặp sốh, k sao cho x = ha + kb .
Bài toán sau cho ta cách phân tích trong một số trường hợp cụ thể.
Bài toán. Cho tam giác ABC với trọng tâm G. Gọi I là trung điểm của đoạn
AG và K là điểm trên cạnh AB sao cho AK = \aB .
5
Hãy phân tích Aỉ, AK, CI, CK theo a = CA, b = CB;
Chứng minh ba điểm c, I, K thẳng hàng.
G/Á/
2
CI = CA + AI = a + ^b-ị-a = ^b + ịa ;	Hìnhl.15
6	3	6	3
a) Gọi ÂD là trung tuyến của tam giác ABC (h. 1.15). Ta có AD = CD-CA = ^b-a.
-z-t	- 17 1 -	1 7 4-
CK = CA + AK - a + --b-^-a--^b + — a.
5	5	5	5
b) Từ tính toán trên ta có CK = —CI. Vậy ba điểm c, I, K thẳng hàng.
Câu hỏi và bài tạp
Cho hình bình hành ABCD. Chứng minh rằng :
Ãổ + ÃC + Ã3 = 2ÃC.
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ AB, BC, CA theo hai vectơ u = AK, V = BM.
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho MB = 3MC. Hãy phân tích vectơ AM theo hai vectơ U - AB và V = AC.
Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng
2DA + 5b + 5c = 0 ;
20A + OB + oc - 4OD, với ơ là điểm tuỳ ý.
Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng :
2MN ^Ãc+ BD = BC+ AD .
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho
3KA + 2KB = Q.
Cho tam giác ASC. Tìm điểm M sao cho MA + MB + 2MC = 6 .
Cho lục giác ABCDEF. Gọi M, N, p, Q, R, s lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Cho tam giác đều ABC có o là trọng tâm và M là một điểm tuỳ ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng
MD + ME + MF = ịÃĨO.
2
Tỉ lệ vàng
ơ-clit (Euclide), nhà toán học của mọi thời đại đã từng nói đến “tỉ íệ vàng” trong tác phẩm bất hủ củạ ông mang tên “Những nguyên tắc cơ bản”. Theo ơ-clit, điểm / trên đoạn AB được gọi là điểm chia đoạn AB theo tỉ lệ vàng nếu thoả mãn
(1)
IB AI '	1 '
Hình 1.16
Đặt x = ậỊ- = ta có AB = xAI và AI = xIB. số X đó được gọi là tỉ lệ vàng và ■ IB AI
điểm I được gọi là điểm vàng của đoạn AB.
Để tính X, ta có thể đặt IB - 1. Từ (1) ta có
X x + 1	.	2	„ „
-7 = —— ,	hay X. - X -1 = 0 ,
1 X
tức là	X =	= 1,61803 .
Với tỉ lệ vàng người ta có thể tạo nên một hình chữ nhật đẹp, cân đối và gây hứng thú cho nhiều nhà hội hoạ kiến trúc. Ví dụ, khi đến tham quan đền Pác-tê-nông ở A-ten (Hi Lạp) người ta thấy kích thước các hình hình học trong đền phẩn lớn chịu ảnh hưởng của tỉ lệ vàng. Nhà tâm lí học người Đức Phít-nê (Fichner) đã quan sát và đo hàng nghìn đồ vật thường dùng trong đời sống như ô cửa sổ, trang giấy viết, bìa sách... và so sánh kích thước giữa chiểu dài và chiều ngang của chúng thì thấy tỉ số gần bằng tỉ lệ vàng.
Hình1.17. Đền Pác-tê-nông và đường nét kiến trúc của nó.
x AB a ó -TT--—-— AI |(75-1)
75 + 1
Hình 1.19
Vẽ tam giác ABC vuông tại s, với BC = ^. Đường tròn tâm c bán kính cắt AC tại E. Đường tròn tâm A bán kính AE cắt AB tại I.
Ta có AC= vàAE = AỈ= ^(75-1). Do đó
Sử dụng điểm vàng ỉ ta có thể dựng được góc 72° , từ đó dựng được ngũ giác đều cũng như ngôi sao năm cánh như sau :
Ta dựng đường tròn tâm I bán kính IA cắt trung trực của IB tại F ta được FAB = 36° và ABF = 72° (h.1.18).
Một ngũ giác đều nội tiếp đường tròn trên có hai đỉnh liên tiếp là F và điểm xuyên tâm đối A' của A. Từ đó ta dựng được ngay ba đỉnh còn lại của ngũ giác đều.
i. „	/1/ ak
Cần lưu ý rằng trên ngôi sao năm cánh trong hình 1.19 thì tỉ sô' -77 = chính là
IK /\I
tỉ lệ vàng. Ngôi sao vàng năm cánh của Quốc kì nước ta được dựng theo tỉ số này.