Giải Toán 11: Bài tập ôn chương III

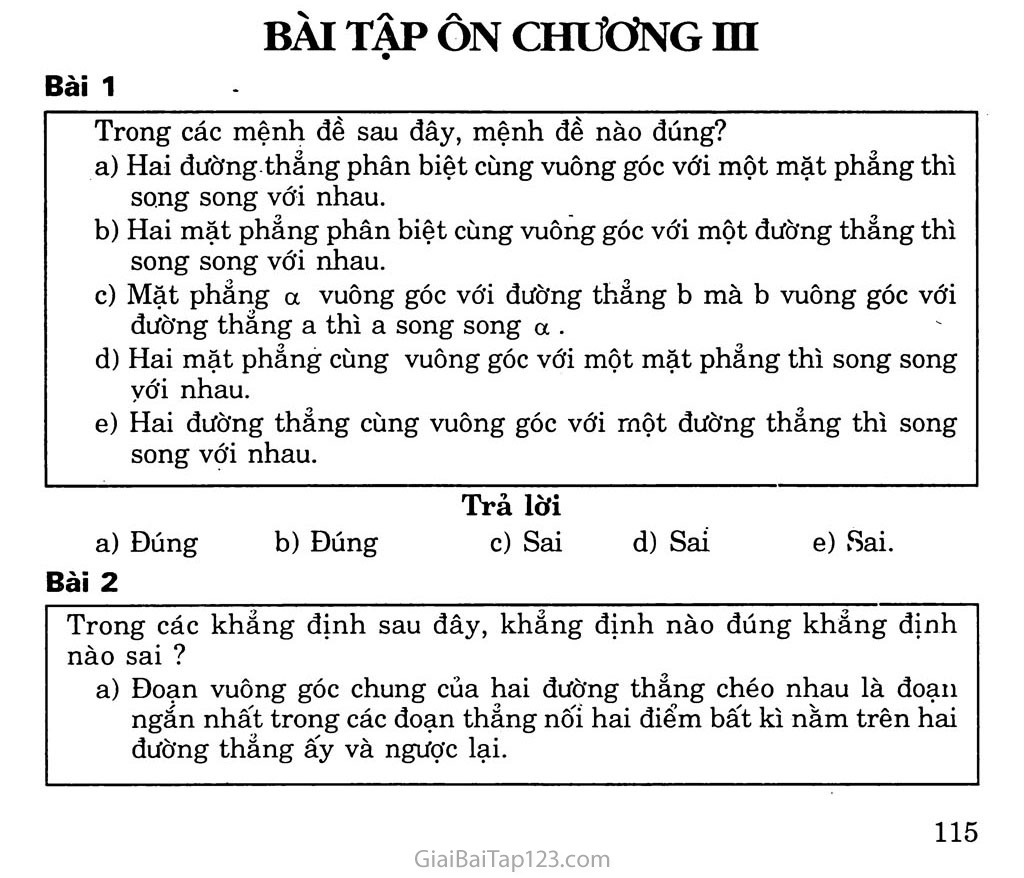
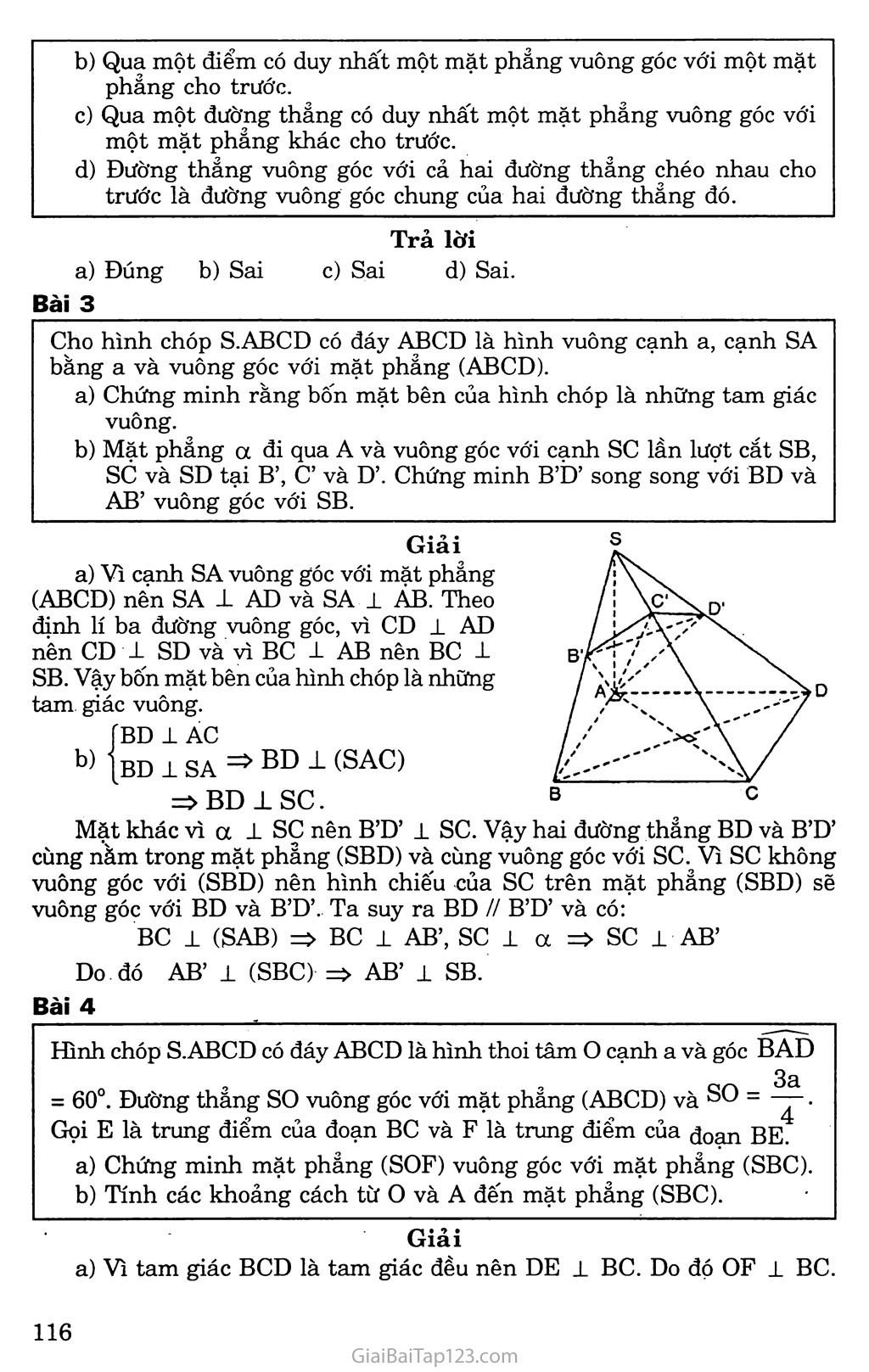
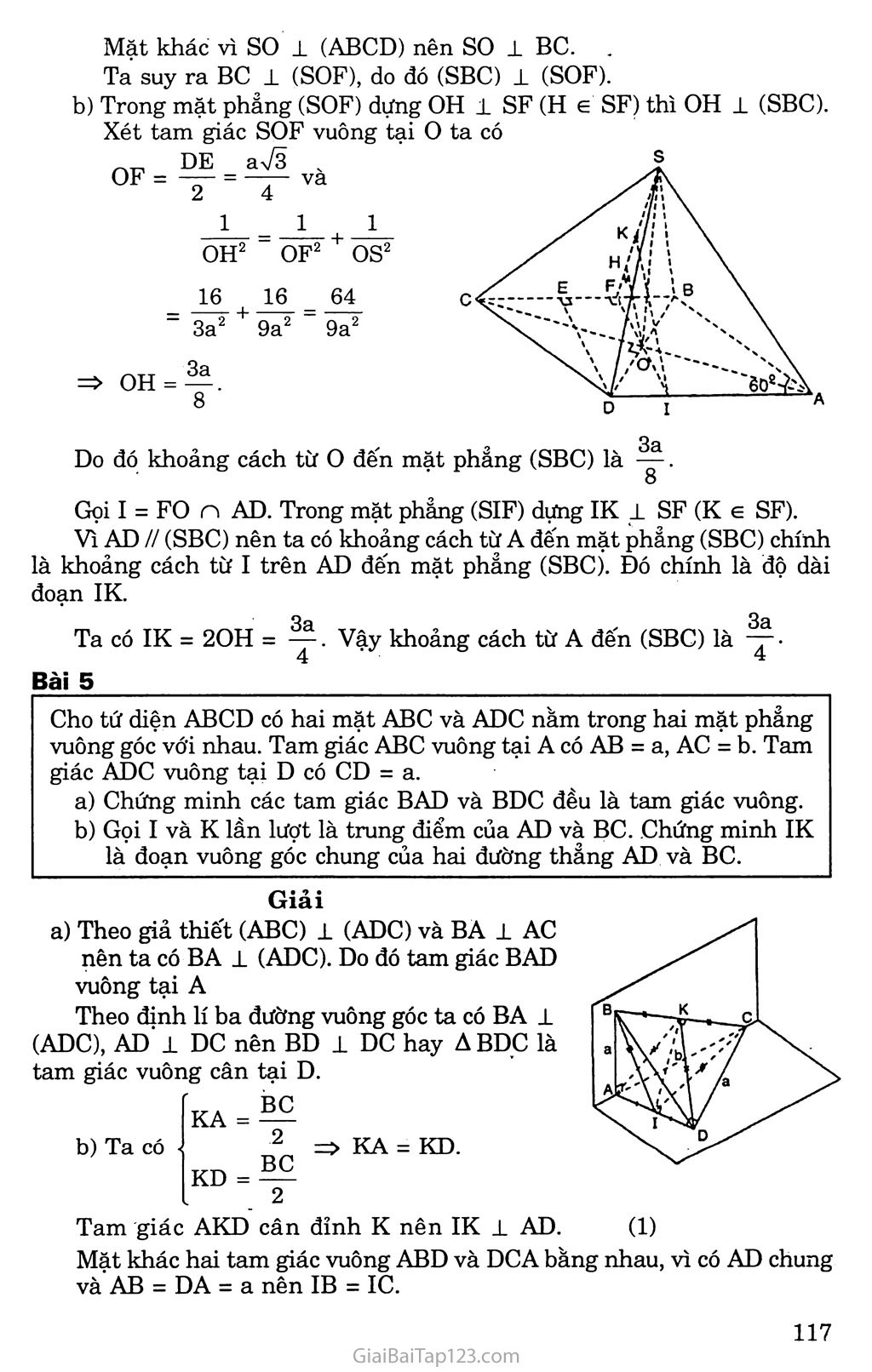
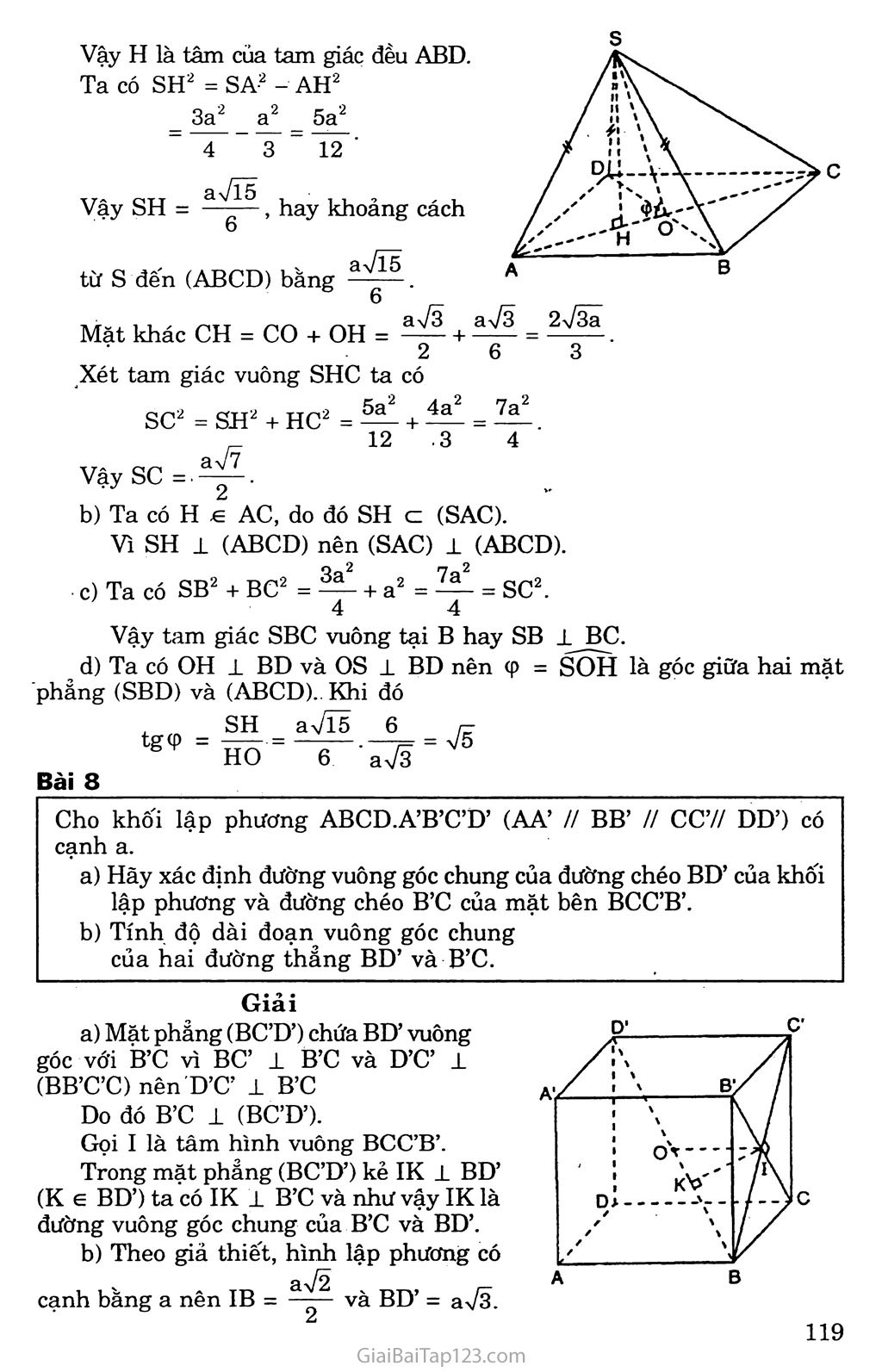
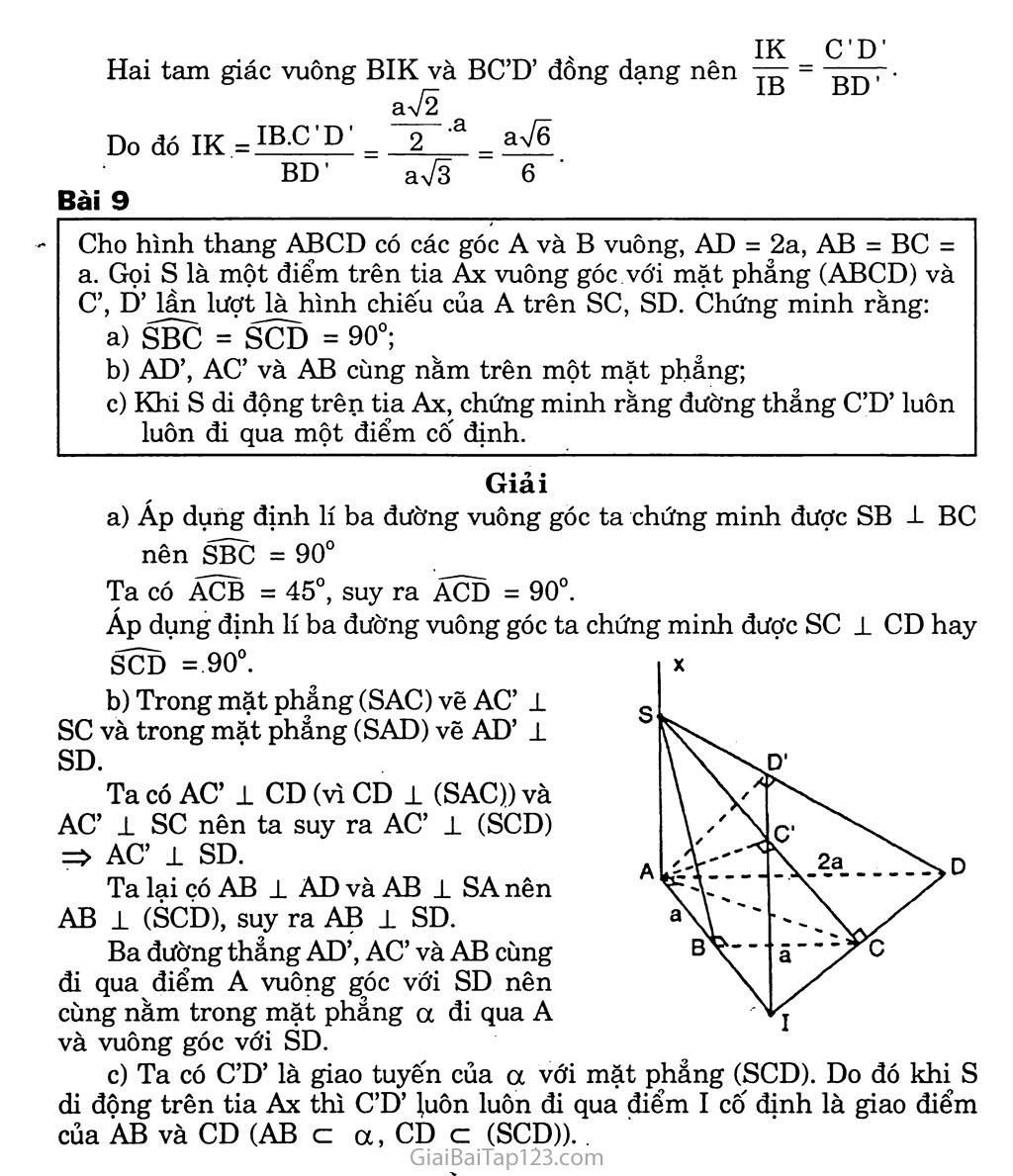
BÀI TẬP ÔN CHƯƠNG HI
Bài 1	-
Trong các mệnh đề sau đây, mệnh đề nào đúng?
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Mặt phẳng a vuông góc với đường thẳng b mà b vuông góc với đường thẳng a thì a song song a .
Hai mặt phảng cùng vuông góc với một mặt phẳng thì song song với nhau.
Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
Trả lời
Đúng b) Đúng	c) Sai d) Saí	e) Sai.
Bài 2	
Trong các khẳng định sau đây, khẳng định nào đúng khẳng định nào sai ?
Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nốí hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.
Đường thẳng vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Trả lời
Đúng b) Sai c) Sai d) Sai.
Bài 3	
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA bằng a và vuông góc với mặt phẳng (ABCD).
Chứng minh rằng bốn mặt bên của hình chóp là những tam giác vuông.
Mặt phẳng a đi qua A và vuông góc với cạnh sc lần lượt cắt SB, sc và SD tại B’, C’ và D’. Chứng minh B’D’ song song với BD và AB’ vuông góc với SB.
Giải
Vì cạnh SA vuông góc với mặt phẳng (ABCD) nên SA ± AD và SA 1 AB. Theo định lí ba đường vuông góc, vì CD 1 AD nên CD -L SD và vì BC -L AB nên BC -L SB. Vậy bốn mặt bên của hình chóp là những tam giác vuông.
fBD 1 AC
[BD 1 SA	1 (SAC)
=>BD±SC.
Mặt khác vì a ± sc nên B’D’ 1 sc. Vậy hai đường thẳng BD và B’D’ cùng nằm trong mặt phẳng (SBD) và cùng vuông góc với sc. Vì sc không vuông góc với (SBD) nên hình chiếu của sc tren mặt phẳng (SBD) se vuông góc với BD và B’D’. Ta suy ra BD // B’D’ và có:
BC 1 (SAB) => BC 1 AB’, SC 1 a => SC 1 AB’
Do đó AB’ 1 (SBC) => AB’ 1 SB.
Bài 4
Hình chóp S.ABCD có đáy ABCD là hình thoi tâm o cạnh a và góc BAD ~ 3a
= 60°. Đường thẳng so vuông góc với mặt phẳng (ABCD) và so = 4 ■ Gọi E là trung điểm của đoạn BC và F là trung điểm của đoan BE
Chứng minh mặt phảng (SOF) vuông góc với mặt phảng (SBC).
Tính các khoảng cách từ o và A đến mặt phảng (SBC).
Giải
Vì tam giác BCD là tam giác đều nên DE ± BC. Do dp OF 1 BC.
Mặt khác vì SO 1 (ABCD) nên so 1 BC.
Ta suy ra BC 1 (SOF), do đó (SBC) 1 (SOF).
b) Trong mặt phẳng (SOF) dựng OH 1 SF (H e SF) thì OH 1 (SBC).
Do đó khoảng cách từ o đến mặt phảng (SBC) là .
8
Gọi I = FO n AD. Trong mặt phảng (SIF) dựng IK ± SF (K e SF).
Vì AD // (SBC) nên ta có khoảng cách từ A đến mặt phẳng (SBC) chính
là khoảng cách từ I trên AD đến mặt phảng (SBC). Đó chính là độ dài đoạn IK.
Ta có IK = 2OH = ^. Vậy khoảng cách từ A đến (SBC) là — ■
Bài 5
Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB = a, AC = b. Tam giác ADC vuông tại D có CD = a.
Chứng minh các tam giác BAD và BDC đều là tam giác vuông.
Gọi I và K lần lượt là trung điểm của AD và BC. .Chứng minh IK là đoạn vuông góc chung của hai đường thẳng AD và BC.
Giải
a) Theo giả thiết (ABC) 1 (ADC) và BA 1 AC nên ta có BA 1 (ADC). Do đó tam giác BAD vuông tại A
Theo định lí ba đường vuông góc ta có BA 1 (ADC), AD 1 DC nên BD 1 DC hay ABDC là tam giác vuông cân tại D.
b) Ta có
KA
KD
BC
2
BC
2
KA = KD.
Tam giác AKD cân đỉnh K nên IK ± AD.
(1)
Mặt khác hai tam giác vuông ABD và DCA bằng nhau, vì có AD chung vàAB = DA = a nen IB = 1C.
Tam giác IBC cân đỉnh I nên IK 1 BC.	(2)
Từ (1) và (2) ta suy ra IK là đoạn vuông góc chung của hai đường thẳng AD và BC.
Bài 6	
Cho khối lập phương ABCD.A’B’C’D’ cạnh a (có AA’//BB7/CC’//DD’j.
Chứng minh BC’ vuông góc với mặt phẳng (A’B’CD).
Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’„
Giải
Ta có: B’C 1 BC’ và A’B’ 1 (BB’C’C)
=> A’B’ 1 BC’
Do đó: BC’ 1 (A’B’CD).
Mặt phẳng (AB’D’) chứa AB’ và song sóng với BC’. Ta cần tìm hình chiếu của BC’ trên mặt phẳng này. Gọi E và F lần lượt là tâm các hình vuuông ADD’A’ và BCC’B’. Trong mặt phẳng (A’B’CD) kẻ FH 1 EB’(H 6 EB’) nên theo câu a, FH 1 BC’ hay FH 1 AD’.
thẳng đi qua H và song song với BC’. Đường thẳng đó cắt AB’ tại K. Từ K ta vẽ KI song song với HF cắt BC’ tại I. Ta có IK là đoạn vuông góc chung của AB’ và BC’. Xét tam'giác vuông EFB’ ta có:
111 FH2 - FE2 + FB '2
'aVfY
I 2 J
a2
Vậy FH 1 (AB’D’). Do đó hình chiếu của BC’ trên mặt phẳng (AB’D’) là đường
Ta tính được IK = FH =
O
Bài 7
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, góc BAD = 60° và SA = SB = SD =
2
Tính khoảng cách từ s đến mặt phảng (ABCD) và độ dài cạnh sc.
Chứng minh mặt phẳng (SAC) vuông góc với mặt phảng (ABCD).
Chứng minh SB vuông góc với BC.
Gọi Ọ là góc giữa hai mặt phẳng (SBD) và CABCD). Tính tg(p.
Giải
Gọi H là hình chiếu vuông góc của s trên mặt phẳng (ABCD) Vì SA = SB = sc =.
2
nên HA = HB = HC.
Xét tam giác vuông SHC ta có
SC2 = SH2 + HC2 = 4^1 + ^ = -7 12	.3	4
VậySC=.~.
Ta có H e AC, do đó SH cz (SAC).
Vì SH 1 (ABCD) nên (SAC) 1 (ABCD).
Ta có SB2 + BC2 =	+ a2 =	= sc2.
Bài 8
Cho khối lập phương ABCD.A’B’C’D’ (AA’ // BB’ // CC7/ DD’) có cạnh a.
Hãy xác định đường vuông góc chung của đường chéo BD’ của khối lập phương và đường chéo B’C của mặt bên BCC’B’.
Tính độ dài đoạn vuông góc chung của hai đường thẳng BD’ và B’C.
Giải
Mặt phẳng (BCT)’) chứa BD’ vuông góc với B’C vì Bơ 1 B’C và D’C’ 1 (BB’CC) nên D’C’ 1 B’C
Do đó B’C 1 (BƠD’).
Gọi I là tâm hình vuông BCC’B’.
Trong mặt phẳng (BC’D’) kẻ IK ± BD’ (K e BD’) ta có IK 1 B’C và như vậy IK là đường vuông góc chung của B’C và BD’.
Theo giả thiết, hình lập phương có
aỢ2	r-
cạnh bằng a nên IB = - -T-- và BD’ = aựã.
Hai tam giác vuông BIK và BC’D’ đồng dạng nên 7^7 = p-p , • r-	*	lh) .dJJ
aV2
Do đó TK =IBC'P' = ~2~Ja = aVẽ BD' aVÕ 6
Bài 9 	
Cho hình thang ABCD có các góc A và B vuông, AD = 2a, AB = BC - a. Gọi s là một điểm trên tia Ax vuông góc với mặt phẳng (ABCD) và C’, D’lẩn lượt là hình chiếu của A trên sc, SD. Chứng minh rằng:
SBC =’ SCD = 90°;
AD’, AC’ và AB cùng nằm trên một mặt phẳng;
Khi s di động trên tia Ax, chứng minh rằng đường thẳng C’D’ luôn luôn đi qua một điểm cố định.
Giải
a) Áp dụng định lí ba đường vuông góc ta chứng minh được SB -L BC nên SBC = 90°
Ta có ACB = 45°, suy ra ACD = 90°.
SCD = 90°.
b) Trong mặt phẳng (SAC) vẽ AC’ 1 sc và trong mặt phảng (SAD) vẽ AD’ 1 SD.
Ta có AC’ 1 CD (vì CD 1 (SAC)) và AC’ 1 sc nên ta suy ra AC’ 1 (SCD) => AC’ 1 SD.
Ta lại có AB 1 AD và AB ± SA nên AB 1 (SCD), suy ra AB 1 SD.
Ba đường thẳng AD’, AC’ và AB cùng đi qua điểm A vuông góc vỡi SD nên cùng nằm trong mặt phảng a đi qua A và vuông góc với SD.
Áp dụng định lí ba đường vuông góc ta chứng minh được sc 1 CD hay
Ta có C’D’ là giao tuyến của a với mặt phảng (SCD). Do đó khi s di động trên tia Ax thì C’D’ Ịuôn luôn đi qua điểm I cố định là giao điểm của ÁB vàCD(AB c a, CD c (SCD))..