Giải Toán 11: Vấn đề 2. Hai đường thẳng vuông góc

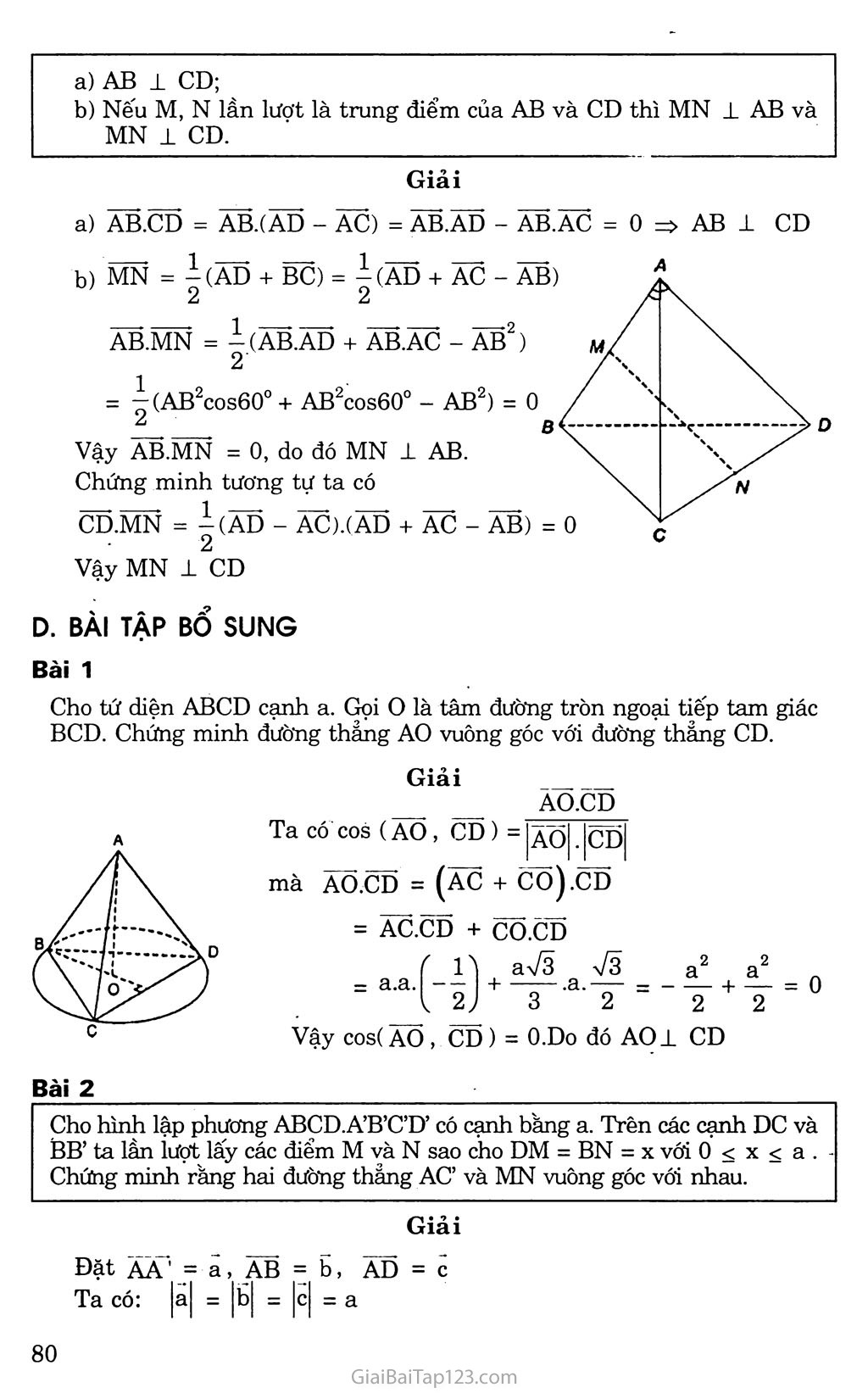
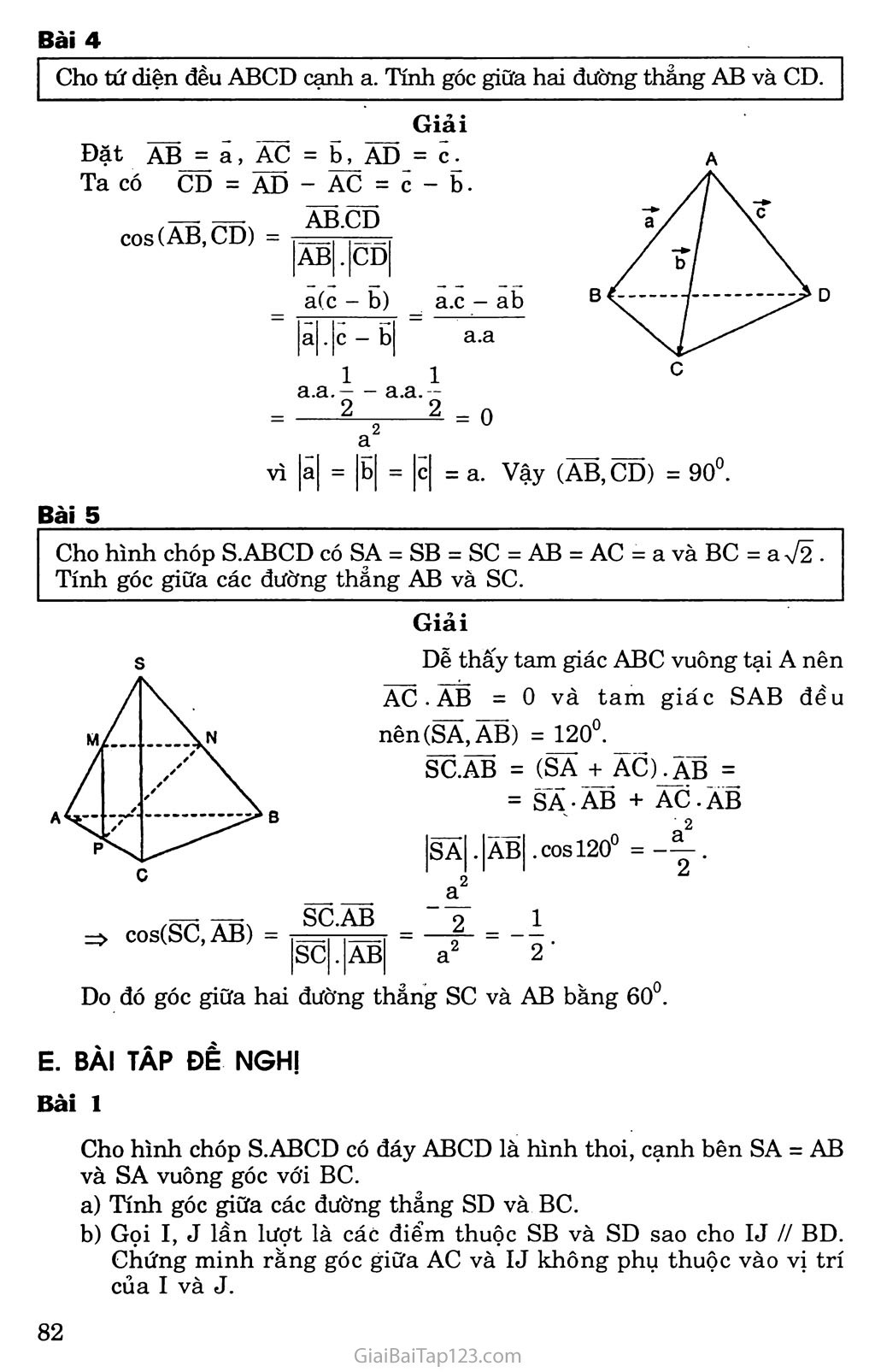
O)ấa đề 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
KIẾN THỨC CẦN NHỚ
I. VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THANG
Vecto' ạ í 0 được gọi là vecto' chỉ phương của đường thẳng d nếu giá của vecto' a song song hoặc trùng với đường thẳng d.
Nếu a là vectơ chỉ phương của đường thẳng d thì mọi vectơ kẵvới k 5Ế 0 cũng là vectơ chỉ phương của d.
Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương a của d.
n. GÓC GIỮA HAI ĐƯỜNG THANG
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm 0 lần lượt song song vói a và b.
III. HAI ĐƯỜNG THẲNG VUÔNG GÓC Hai đường thẳng a và b được gọi là vuông góc với nhau nếu góc giữa
chúng bằng 90°. Ta kí hiệu a 1 b hoặc b ± a.
Nếu ũ và V lần lượt là các vectơ chỉ phương của hai đường thẳng a và
b thì a 1 b u.v = 0.
Nếu a // b và c vuông góc với một trong hai đường thẳng đó thì c vuông góc với đường thẳng còn lại.
PHƯƠNG PHÁP GIẢI TOÁN
Để chứng minh hai đường thẳng AB và CD vuông góc nhau, ta chỉ cần chứng minh: AB.CD - 0
Để tính số đo của góc giữa 2 đường thẳng (dj) và (d2) ta có thể thực hiện như sau:
Tìm các vectơ chi phương của hai đường thẳng này, giả sử các vectơ chỉ phương ấy là u và V.
Gọi a là góc giữa 2 đường thẳng (d^ và (d2) ta có: cosot = Ịcos(u,Ỹ)|
c. GIẢI BẶI TẬP SÁCH GIÁO KHOA
Bài 1	
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
a) ÃB và EG;	b) ÃF và EG;	c) ÃB và DH.
Giải
a) (ÃB, ẼG) = 45°; b)(ÃF, ẼG) = 60°; c)(ÃB, DH)=90°.
Bài 2	
Cho tứ diện ABCD.
Chứng minh rằng AB. CD + AC.DB+ AD.BC = 0
b) Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có AB 1 CD và AC 1 DB thì AD 1 BC.
Giải
a) ÃB.CD = AB.(ÃD - ĂC)
AB.CD + AC.DB + AD.BC = 0
AC.	DB = ÃC.(ÃB - ÃD)
AD.	BC = ÃD.(ÃC - ÃB)
b) AB.CD = 0, AC.DB = 0 => AD.BC = 0 => AD 1 BC.
Bài 3	
Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì a và b có song song với nhau không?
Trong không ậian nếu đường thẳng a vuông góc với đường thẳng b và đường thang b vuông góc với đường thẳng c thì a có vuông góc với c không?
Giải
a và b nói chung không song song
a và c nói chung không vuông góc.
Bài 4	 	
Cho hai tam giác đều ABC và ABC’ trong không gian có chung cạnh AB và nằm trong hai mặt phảng khác nhau. Gọi M, N, p và Q lần lượt là trung điểm của các cạnh AC, CB, BC’ và C’A. Chứng minh rằng:
AB i cơ;
Tứ giác MNPQ là hình chữ nhật;
g/g
Tính diện tích hình chữ nhật nói trên, cho biết cc' •= —T—
và AB = a.	2
Giải
a) Ta có CC'.AB = (AC - AC).AB = AC.AB - AC.ĂB Đặt AB = a ta có Aơ= AB = AC = a.
Do đó AC'.AB = a.a.cos60°
AC. AB = a.a.cos60°.
Vậy cc '.AB = 0 và suy ra AB 1 CC’ yx
Vi MN // AB và PQ // AB nên MN // PQ.
Mặt khác MQ // Cơ và NP // CC’ nên MQ // NP.
Vậy tứ giác MNPQ là hình bình hành. Hơn nữa MN ± NP (vì AB 1 Cơ) nên nó là hình chữ nh.it.
Gọi H là trung điểm của đoạn
AB. Ta có CH = CH = vì AB = a.
2
1	1 aVõ a 76	, AB a
D„đóNP= iCC’=	gv»MN. — = j.
Gọi diện tích hình chữ nhật MNPQ là s, ta có
Bài 5
Cho hình chóp tam giác S.ABC có SA = SB - sc và có ASB = BSC = CSA Chứng minh rằng SA 1 BC, SB 1 AC, sc 1 AB.
Giải
SA.BC = SÃ (SC - SB) = SA. sc - SA.SB = 0
Do đó SA ± BC. Tưong tự ta chứng minh được SB ± AC, sc ± AB.
Bài 6
Trong không gian hai hình vuông ABCD và ABƠD’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm 0 và O’. Chứng minh rằng AB 1 00’ và tứ giác CDD’C’ là hình chữ nhật.
Giải
Học sinh vẽ hình.
ÃB.ÕC = ÃB.(ÃÕ*' - ÃÕ) = ÃẼ.ÃÕ*’ - ÃB.ÃÕ = 0 => AB 1 00’ Tứ giác CDD’C’ là hình bình hành có CC’ 1 AB nên CC’ ± CD.
Do đó hình bình hành CDD’C’ là hình chữ nhật.
Bài 7	
Cho s là diện tích của tam giác ABC. Chứng minh rằng:
s = |^ÃB2.ÃC2 -(ÃB.ÃC)2 2
Giải
Ta có SABC = |aB.AC sin A = ỈAB.AC 7l - COS2 A .
AB.AC	r,	ZTT7 AB2.AC
-,7—7 nên VI - COS A = J-	—
(AB.
2 2
Vì cosA =
IabI.IacI
AB .AC
ÃC)2
Do đo SABC = I 7AB2. AC2 - (AB. AC)2
Bài 8	
Cho tứ diện ABCD có AB = AC = AD và BAC = BAD = 60°. Chứng minh rằng:
AB ± CD;
Nếu M, N lần lượt là trung điểm của AB và CD thì MN ± AB và
MN .1 CD.
Giải
AB.CD = ÃB.1ÃD - ĂC) = ÃB.ÃD - ÃB.ÃC = 0 zz> AB 1 CD
MN = |(ÃD + BC) = |(ÃD + ÃC - ÃB)	A
2 2
AB.MN = ị.(ÃB.ÃD + ÃB.ÃC - ÃB2)
2
= |(AB2cos60° + AB2cos60° - AB2) = 0
2_	 8
Vậy AB.MN = 0, do đó MN 1 AB.
Chứng minh tương tự ta có
CD.MN = ị(ÃD - ÃC).(ĂD + ÃC - ÃB) =
2
Vậy MN 1 CD
D. BÀI TẬP BỔ SUNG
Bài 1
Cho tứ diện ABCD cạnh a. Gọi o là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh đường thẳng AO vuông góc với đường thẳng CD.
Giải ___
AO.CD
Ta có COS (Aố , CD ) = |ÃÕ| Ịcĩ5| mà A0.CD = (Ãc + co).CD
= AC.CD + CO.CD
= a.a.
„2	„2
a	a
~2 + T
n a Vã _ 73 „ + —„ -a- „ 2J 3	2
Vậy cos( AO , CD ) = O.Do đó AO± CD
Bài 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Trên các cạnh DC và BB’ ta lần lượt lấy các điểm M và N sao cho DM = BN = X vói 0 < X < a . Chứng minh rằng hai đường thẳng AC’ và MN vuông góc vói nhau.
Giải
Đặt ÃÃ' = a, AB = b, AD = c Ta CÓ: |a| - |b| = c| = a
Và AC' - AA' + AB + AD
hay AB ’ = a + b + c.
Mặt khác MĨ? = AN - AM
= (ÃB + bn) - (ad + dm)
■H+R+r-K)1--
D'
|a+ l-^|b-c ala
a
A'j.
' N B'
Ta CÓ AC'.MN = (a+b+ c).
	 X-2	x^r2 -2, „ - _	_ _
AC'.MN = ^a + ự - -Jb - c (vi a. b = 0, b. c = 0,
x? „2	„2 A z s -2 C2	-2	2,
= 0)
AC'.MN = x.a + 1 + — a - a = 0 (vi a = b = c = a ) Do đó AC’ 1 MN.
Bai_3	
Cho hình lập phương ABCD.A’B’C’D’.
Tính góc giữa hai đường thẳng AC và DA’.
Chứng minh BD 1 AC’
Giải
AB = ă,
ÃD = b, ÃÃ' = C Ta có AC = AB + ÃD = a + b DÃ' = AA” - ÃD = c - b
COS (AC, DÔ') =	T~.i = r + ri ’r - ri
|aC.||DA'| |a + b|.|c-b|
Giả sử hình lập phương có cạnh bằng X ta có:
a.c - a.b + b.c - b _ -X2 2x2
a) Đặt
A'
• 1 '<. I • <
i ' •
1 / Dj-
B /
Ị ''x
1 /	
• ,
1 '
1 /
COS (AC, DÃ') =
xV2.xV2
(Vì ã.c = 0, a.b = 0, b.c = 0 và b2 - X2)
Vậy (AC, DÃ') = 120°
Ta suy ra góc giữa hai đường thẳng AC và DA’ bằng 60°. b) Ta cần tính góc giữa hai vectơ BD và AỠ.
Ta có BD = ÃD - AB, Ãcỵ= AB + ÃD + ÃÃT'.
Vậy BD-Ãc‘' = (ÃD -ÃB). (ÃẼ + ÃD + ÃÃ7')
= (b-a)(a + b + c)
= b.a + b2+ b.c - ã2- a.b - a.c = 0+ b2 + 0 - a2+ 0- 0 = 0
Vậy BD 1 AC’.
Bài 4	
Cho tứ diện đều ABCD cạnh a. Tính góc giữa hai đường thẳng AB và CD.
Giải
vì |ã| = |b| = |c| = a. Vậy (AB,CD) = 90°.
=> cos(SC, AB) =
Bài 5
Cho hình chóp S.ABCD có SA = SB = sc = AB = AC = a và BC = a 72 . Tính góc giữa các đường thẳng AB và sc.
Giải
Dễ thấy tam giác ABC vuông tại A nên AC. AB = 0 và tam giác SAB đều nên(SÃ,ÃB) =JL20°.
SC.AB = (SÃ + AC)^AB =
= SẶ-AB + AC.AB
' n a2
SA . ẦB . COS 120° = -2-
SC.AB 2	1
scI.IabI =	= 2'
Do đó góc giữa hai đường thẳng sc và AB bằng 60°.
E. BÀI TÂP ĐỀ NGHỊ Bài 1
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, cạnh bên SA = AB và SA vuông góc với BC.
Tính góc giữa các đường thẳng SD và BC.
Gọi I, J lần lượt là các điểm thuộc SB và SD sao cho IJ // BD. Chứng minh rằng góc giữa AC và IJ không phụ thuộc vào vị trí của I và J.
Bài 2
Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng a, BAD = 60°, BAA5 = DÃA’= 120°.
Tỉnh góc giữa các cặp đường thẳng AB và A’D và AC’ với B’D.
Tính diện tích các hình A’B’CD và ACC’A’.
Tính góc giữa đường thẳng AC’ và các đường thẳng AB, AD, AA’.
Bài 3
Cho tứ diện ABCD trong đó góc giữa hai đường thẳng AB và CD bằng a . Gọi M là điểm bất kì thuộc cạnh AC, đặt AM = X (0 < X < AC). Xét mặt phẳng (P) đi qua điểm M và song song với AB, CD.
Xác định vị trí điểm M để diện tích thiết diện của hình tứ diện ABCD khi cắt bởi mp(P) đạt giá trị lớn nhất.
Chứng minh rằng chu vi thiết diện nêu trên không phụ thuộc vào X khi và chỉ khi AB = CD.
Bài 4
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AD = 2AB, mặt bên SAB là tam giác vuông tại A. Với điểm M bất kì thuộc cạnh AD (M khác A và D), xét mặt phảng (a ) đi qua điểm M và song song với SA, CD.
Thiết diện của hình chóp S.ABCD khi cắt bởi mp( a) là hình gì?
Tính diện tích thiết diện theo a và b; biết AB = a, SA - b, M là trung điểm của AD.
Bài 5
Cho tứ diện ABCD. Lấy các điểm M và N lần lượt thuộc các đường thẳng BC và AD sao cho MB = kMC và NA = kND với k là số thực cho trước. Đặt a là góc giữa các vecto' MN và BA; p là góc giữa các vecto' MN và CD. Tìm mối liên hệ giữa AB và CD để a = p = 45°.
Bài 6
Cho tứ diện ABCD. Gọi I, J, H, K lần lượt là trung điểm của BC, AC, AD, BD. Hãy tính góc giữa đường thẳng AB với CD trong các trường họp sau:
UHK là hình thoi có đường chéo IH bằng 73 IJ.
IJHK là hình chữ nhật.
Bài 7	’	4	 	
Cho tứ diện ABCD có CD = AB. Gọi I, J, K lần lượt là trung điểm 3	5
của BC, AC, BD. Cho biết JK = 6 AB, tính góc giữa đường chẳng CD với các đường thẳng IJ và AB.
Bài 8
Cho tứ diện ABCD có tất cả các cạnh bằng nhau. Gọi M và N lần lượt là trung điểm của AB và CD. Lấy các điểm I, J, K lần lượt thuộc các đường thẳng BC, AC, AD sao cho ĨB = kĩc, JA = k JC, KA = kKD trong đó k là số cho trước.
Chứng minh rằng MB ± IJ và MN ± JK.
Chứng minh rằng AB ± CD.