Giải Toán 11: Vấn đề 3. Đường thẳng vuông góc với mặt phẳng

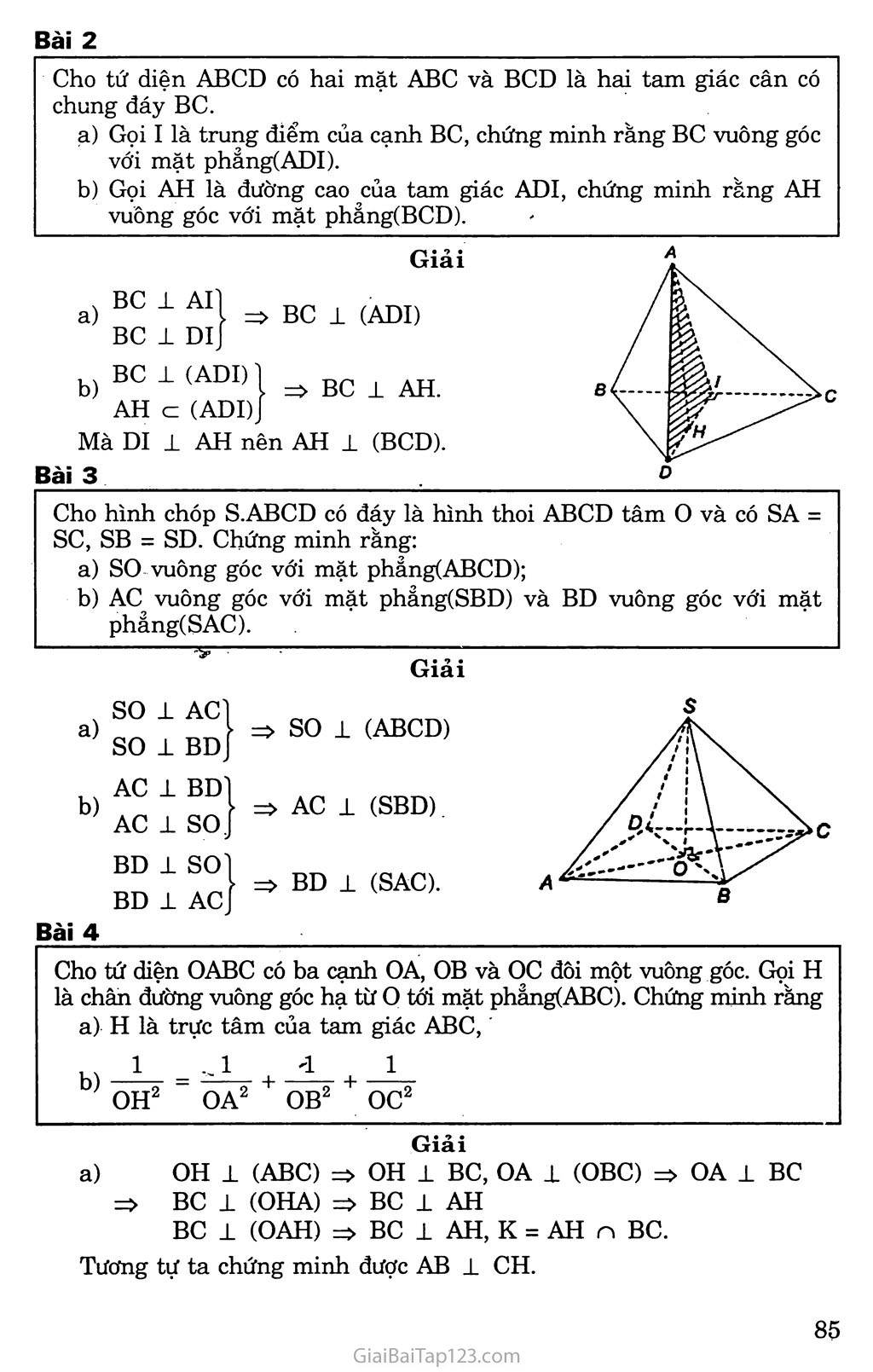
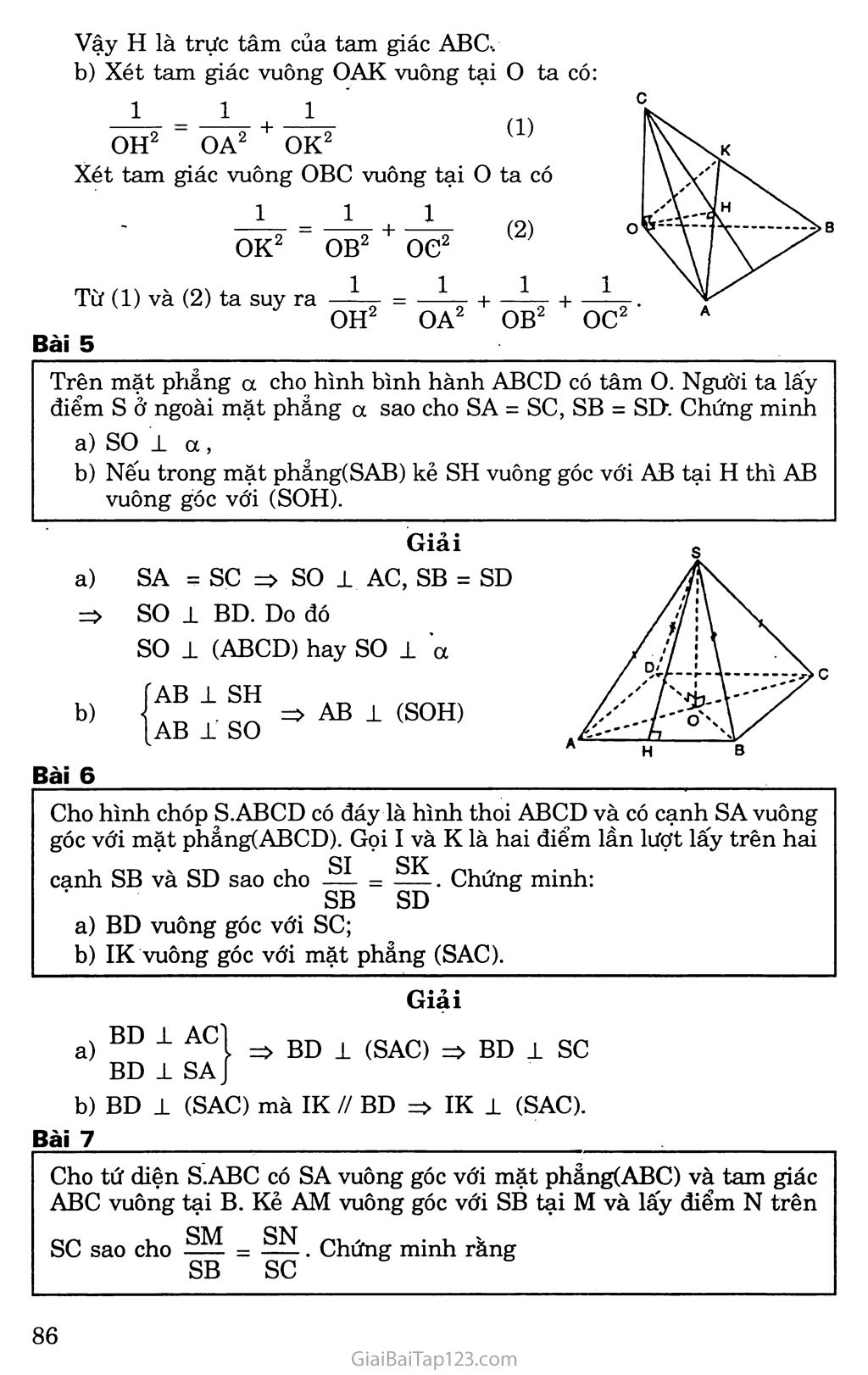
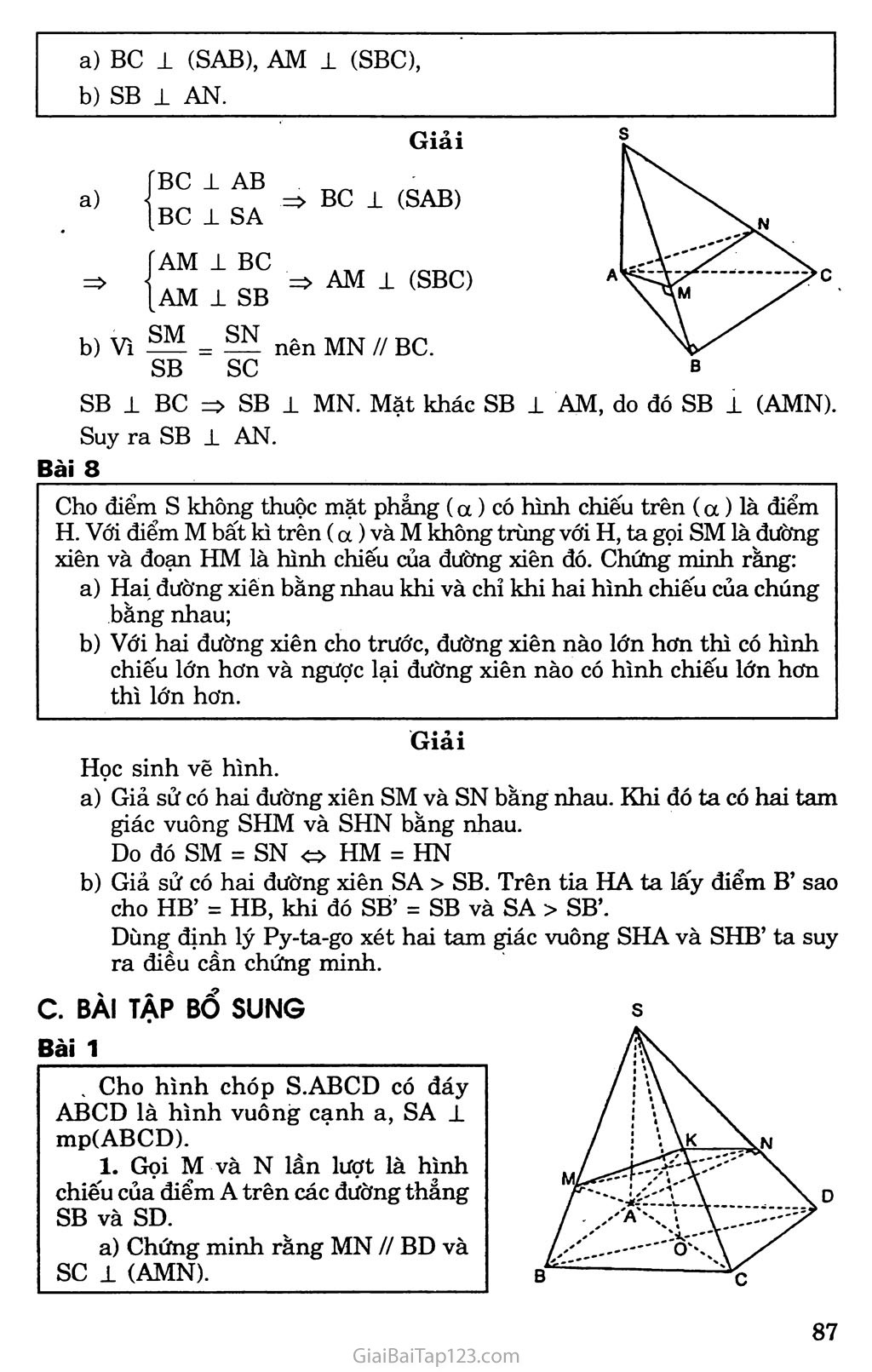
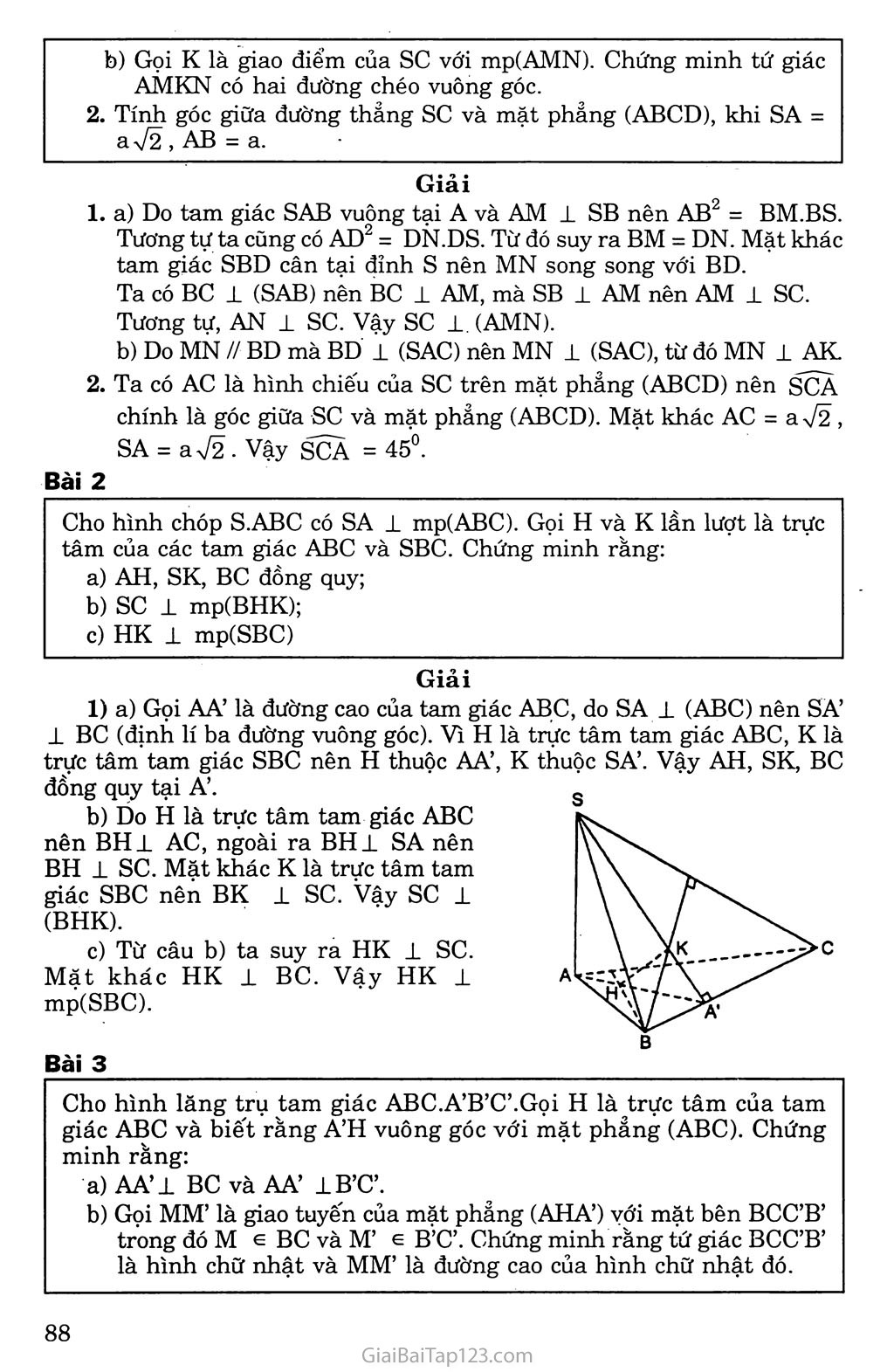
Om, đề 3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
KIẾN THỨC CẦN NHỚ
Định nghĩa đường thẳng vuông góc với mặt phẳng
Định nghĩa:
Một đườnặ thẳng gọi là vuông góc VỚỊ mặt phảng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau trong mặt phẳng thì đường thẳng ấy sẽ vuông.góc với mặt phẳng đó.
Định lí ba đường vuông góc
Cho đườn^ thẳng a có hình chiếu trên mp(P) là đường thẳng a’. Khi ấy một đường thang b nằm trong mặt phảng (P) vuông góc với a khi và chỉ khi nó vuông góc với a’.
Góc giữa đường thẳng và mặt phẳng
Định nghĩa:
Nếu đường thẳng a vuông góc với mp(P) thì ta nói rằng góc giữa đường thẳng a và mp(P) bằng 90°.
Nếu đường thẳng a không vuông góc với mp(P) thì góc giữa a và hình chiếu a’ của nó trên (P) gọi là góc giữa đường thẳng a và mp(P).
PHƯƠNG PHÁP GIẢI TOÁN
Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh đường thẳng d vuông góc vói mặt phẳng (P), ta chúng minh d vuông góc vói hai đưòng thẳng a và b cắt nhau cùng nằm trong (P).
Chứng minh đường thẳng vuông góc với đường thẳng.
Cách 1: Để chứng minh hai.đưòng thẳng vuông góc vói nhau, ta chứng minh
đưòng thẳng này vuông góc vói một mặt phẳng chứa đường thẳng kia.
Cách 2. Dùng định lí ba đường vuông góc.
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1	
Cho hai đường thẳng a, b và mặt phẳng (a). Các mệnh đề sau đây
đúng hay sai?
a) Nếu a // (a ),
và
b 1 (a) thì a 1 b.
b) Nếu a // (a ),
và
b ± a thì b ± (a ).
c) Nếu a // (a ),
và
b // (a ) thì b // a.
d) Nêu a± (a),
và
b ± a thì b // (a ).
Trả lời
a) Đúng	b) Sai	c) Sai	d) Sai.
Bài 2
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC.
Gọi I là trung điểm của cạnh BC, chứng minh rằng BC vuông góc với mặt phẳng(ADI).
Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng(BCD).
Giải
1 All BC ± (ADD BC 1 DIJ
BC 1	=> BC 1 AH.
AH c (ADDJ
Mà DI 1 AH nên AH 1 (BCD).
Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm o và có SA = SC, SB = SD. Chứng minh rằng:
SO vuông góc với mặt phẳng(ABCD);
AC vuông góc với mặt phẳng(SBD) và BD vuông góc với mặt phẳng(SAC).
' 	
Giải
SO
1
AC
so
1
BD
AC
1
BD
AC
1
SO;
BD
1
SO
BD
1
AC
=> so 1 (ABCD)
=> AC 1 (SBD).
=> BD 1 (SAC).
Bài 4	
Cho tứ diện OABC có ba cạnh OA, OB và oc đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ o tới mặt phẳng(ABC). Chứng minh rằng a) H là trực tâm của tam giác ABC,
1	= „1	'1 J_
b OH2 OA2 + OB2 + oc2
Giải
a) OH 1 (ABC) => OH 1 BC, OA 1 (OBC) OA 1 BC => BC 1 (OHA) => BC ± AH
BC 1 (OAH) => BC 1 AH, K = AH n BC.
Tương tự ta chứng minh được AB 1 CH.
Vậy H là trực tâm của tam giác ABC-, b) Xét tam giác vuông OAK vuông tại o ta có 111
OH
OA OK2
Xét tam giác vuông OBC vuông tại o ta có 1 11
OK2
Từ (1) và (2) ta suy ra
Bài 5
OB2
1
OH2
oe2
1
OA2
Trên mặt phẳng a cho hình bình hành ABCD có tâm o. Người ta lấy điểm s ở ngoài mặt phẳng a sao cho SA - sc, SB = SD. Chứng minh
SO la,
Nếu trong mặt phẳng(SAB) kẻ SH vuông góc với AĐ tại H thì AB vuông góc với (SOH).
a)
b)
Bài 6
Giải
SA = SC => SO 1 AC, SB = SD
SO 1 BD. Do đó
SO 1 (ABCD) hay so 1 a
ÍAB 1 SH AB i SO
AB 1 (SOH)
Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng(ABCD). Gọi I và K là hai điểm lần lượt lấy trên hai
cạnh SB và SD sao cho -§1 - ỆỊS. Chứng minh:
SB SD
BD vuông góc với SC;
Giải
BD 1 (SAC) => BD 1 sc
BD 1 ACl
a)
IK vuông góc với mặt phẳng (SAC).
BD 1 SA
b) BD 1 (SAC) mà IK // BD => IK 1 (SAC).
Bài 7	
Cho tứ diện S.ABC có SA vuông góc với mặt phẳng(ABC) và tam giác ABC vuông tại B. Kẻ AM vuông góc với SB tại M và lấy điểm N trên
sc sao cho	. Chứng minh rằng
SB sc
BC 1 (SAB), AM 1 (SBC),
SB 1 AN.
a)
BC ± AB BC JL SA
AM 1 BC AM 1 SB
Giải
BC 1 (SAB)
AM 1 (SBC)
b) Vi fM = nên MN // BC.
SB SC
SB i BC => SB 1 MN. Mặt khác SB 1 AM, do đó SB i (AMN). Suy ra SB ± AN.
Bài 8	
Cho điểm s không thuộc mặt phẳng (a) có hình chiếu trên (a ) là điểm H. Với điểm M bất kì trên (a ) và M không trùng với H, ta gọi SM là đường xiên và đoạn HM là hình chiếu của đường xiên đó. Chứng minh rằng:
Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Giải
Học sinh vẽ hình.
Giả sử có hai đường xiên SM và SN bằng nhau. Khi đó ta có hai tam giác vuông SHM và SHN bằng nhau.
Do đó SM = SN HM = HN
Giả sử có hai đường xiên SA > SB. Trên tia HA ta lấy điểm B’ sao cho HB’ = HB, khi đó SB’ = SB và SA > SB’.
Dùng định lý Py-ta-go xét hai tam giác vuông SHA và SHB’ ta suy ra điều cần chứng minh.
c. BÀI TẬP BỔ SUNG
Bài 1	
. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA 1 mp(ABCD).
Gọi M và N lần lượt là hình chiếu của điểm A trên các đường thẳng SB và SD.
a) Chứng minh rằng MN // BD và SC 1 (AMN).
b) Gọi K là giao điểm của sc với mp(AMN). Chứng minh tứ giác AMKN có hai đường chéo vuông góc.
Tính góc giữa đường thẳng sc và mặt phẳng (ABCD), khi SA = a 42 , AB = a.
Giải
a) Do tam giác SAB vuông tại A và AM ± SB nên AB2 = BM.BS. Tương tự ta cũng có AD2 = DN.DS. Từ đó suy ra BM = DN. Mặt khác tam giác SBD cân tại đỉnh s nên MN song song với BD.
Ta có BC ± (SAB) nên BC ± AM, mà SB ± AM nên AM ± sc. Tương tự, AN 1 sc. Vậy sc 1 (AMN).
b) Do MN //• BD mà BD 1 (SAC) nên MN 1 (SAC), từ đó MN 1 AK.
Ta có AC là hình chiếu của sc trên mặt phẳng (ABCD) nên SCA chính là góc giữa sc và mặt phảng (ABCD). Mặt khác AC = a 42 , SA = a VÍ. Vậy SCA = 45°.
Bài 2	
Cho hình chóp S.ABC có SA 1 mp(ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
AH, SK, BC đồng quy;
SC 1 mp(BHK);
HK 1 mp(SBC)
Giải
1) a) Gọi AA’ là đường cao của tam giác ABC, do SA ± (ABC) nên SA’ 1 BC (định lí ba đường vuông góc). Vì H là trực tâm tam giác ABC, K là trực tâm tam giác SBC nên H thuộc AA’, K thuộc SA’. Vậy AH, SK, BC đồng quy tại A’.
->c
Do H là trực tâm tam giác ABC nên BH± AC, ngoài ra BH± SA nên BH ± sc. Mặt khác K là trực tâm tam giác SBC nên BK 1 sc. Vậy sc 1 (BHK).
Từ câu b) ta suy ra HK 1 sc.
Mặt khác HK 1 BC. Vậy HK 1 mp(SBC).
Bài 3
Cho hình lăng trụ tam giác ABC.A’B’C’.Goi H là trực tâm của tam giác ABC và biết rằng A’H vuông góc với mặt phảng (ABC). Chứng minh rằng:
AA’l BC và AA’ 1B’C’.
Gọi MM’ là giao tuyến của mặt phảng (AHA’) với mặt bên BCƠB’ trong đó M e BC và M’ G B’ơ. Chứng minh rằng tứ giác BCƠB’ là hình chữ nhật và MM’ là đường cao của hình chữ nhật đó.
Giải
BC 1 AH => BC 1 A’H vì A’H 1 (ABC).
BC 1 (A’HA) => BC i AA’ và B’C’1 AA’ vì BC // B’C.
Ta có AA’ // BB’ // CC’ mà BCl AA’ nên tứ giác BCƠB’ là hình chữ nhật.
Vì AA’ // (BCC’B’) nên AA’// MM’và vì AA’ ± BC nên ta suy ra MM’ ± BC và
MM’B’C’ hay MM’ là đường cao của hình chữ nhật BCC’B’.
Bài 4
Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của điểm B qua trung điểm o của cạnh BC. Chứng minh rằng CD 1 CA và CD 1 (SCA).
Giải
Ta có SA 1 (ABC)
SA ± DC c (ABC)
Vì AC và BD cắt nhau tại trung điểm o của mỗi đoạn nên tứ giác ABCD là hình bình hành và ta có AB //DC. Vì AB ± AC nên CD ± CA.
Mặt khác ta có CDl SA, do đó CD 1 (SCA).
Bài 5
Chứng minh BC ± AD.
Gọi AH là đường cao của tam giác ADL
Giải
Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.
Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI 1 BC. Tương tự tam giác DBC cân đỉnh D và có I là trung điểm của BC nên DI ± BC. Ta suy ra:
BC ± (AID) và BC 1 AD.	1
Vì BC 1 (AID) nên BC 1 AH.
Mặt khác AH ± ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).
Bài 6	
Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có SB = SD = AB
1/ Chứng minh rằng mp(SAC) là mặt phẳng trung trực của đoạn thẳng BD.
2/ Chứng minh tam giác ASC vuông tại s.
2/ Từ giả thiết, ta có:
Giải
1/ Do ABCD là hình thoi nên AC ± BD (1) Gọi o là tâm hình thoi ABCD thì OB - OD. Theo bài ra: SB = SD
AABD cân nên so ± BD (2)
SB = SD = AB = AD = CB = CD
Cạnh BD chung, nên
AABD = ASBD = ACBD (c. c. c)
Suy ra: OA = OS = oc.
Vậy, ASAC vuông tại s.
Từ (1), (2) suy ra: BD 1 mp(SAC) tại o, nên mp(SAC) là mặt phẳng trung trực của đoạn thẳng BD.
D. BẰI TẬP ĐỀ NGHỊ
Bài 1
Cho tứ diện SABC có SA -L mp(ABC). Gọi H và K lần lượt là trực tâm của hai tam giác ABC và SBC. Chứng minh:
1/ SC 1 mp(BHK)
2/ HK 1 mp(SBC)
Bài 2
Cho hình chóp S.ABCD có: AB = BC = AC = a; SA = SB = sc = b. Gọi G là trọng tâm AABC . Chứng minh SG 1 mp(ABC) và hãy tính SG theo a và b.
Bài 3
Cho tam giác vuông ABC có cạnh huyền BC - a. Một điểm M trong không gian thỏa MA = MB = MC = b. Vẽ MH ± mp(ABC). Tính độ dài MH theo a và b.
Bài 4
Cho tam giác cân ABC có đáy BC nằm trên mp(P). Gọi A’ là hình chiếu của A trên mp(P). Biết BC = 16, AA’ = 6 và A’BC là tam giác vuông. Tính đường cao của tam giác ABC vẽ từ A.
Bài 5
Trên mặt phẳng (a ) cho tam giác ABC vuông tại A, có AB = a, ABC
= 60°. H e AC sao cho AH = 2HC; SH =	, I là trung điểm BC.
1/ Chứng minh rằng các mặt bên của hình chóp SABCD là các tam giác vuông. Tính SA, SB, sc.
2/ Chứng minh các tam giác SIA, HIA là các tam giác vuông.
Bài 6
Cho hai hình chữ nhật ABCD và ABEF không đồng phẳng có hai
đường chéo AC và BF vuông góc. Vẽ CH ± BE và FK ± DA.
1/ Chứng minh các tam giác ACH và BFK là các tam giác vuông.
2/ Chứng minh AH ± BF và BK ± AC.
Bài 7
Cho hình chóp S.ẠBC có SB vuông góc với mp(ABC), ABC là tam giác vuông tại A.
Chứng minh rằng ACS là tam giác vuông.
Tính SA, SB, sc biết rằng ACB = ữ., ACS = p và BC = a.
Bài 8
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, cạnh bên SA vuông góc với mp(ABCD), SA - a và ABC = 60°.
Tính SB, sc, SD.
Gọí I là trung điểm của sc. Chứng minh rằng IB = ID.
Bài 9
Cho tam giác đều ABC có cạnh bằng a. Gọi A là đường thẳng vuông góc với mp(ABC) kẻ từ A. Với điểm M bất kì thuộc À, M .^A, gọi K là trực tâm của tam giác MBC và A! là đường thẳng đi qua K và vuông góc với mp(MBC).
Chứng minh rằng Aj đi qua điểm cố đỉnh khi M-thay đổi trên A.
Chứng minh Aj -cắt A tại điếm N và BM ± CN, CM ± BN. Xác định vị trí điếm M để độ dài MN đạt giá trị bé nhất.
Bài 10
Cho hình chóp s.ABC có đáy ABC là tam giác đều, SA = SB = sc = a và cùng tạo với mặt phảng (ABC) góc 60°. Một mặt phẳng song song với hai cạnh chéo nhau của hình chóp và cắt hình chóp đó theo thiết diện là hình vuông. Tính diện tích thiết diện đó.