Giải Toán 11: Vấn đề 4. Hai mặt phẳng song song

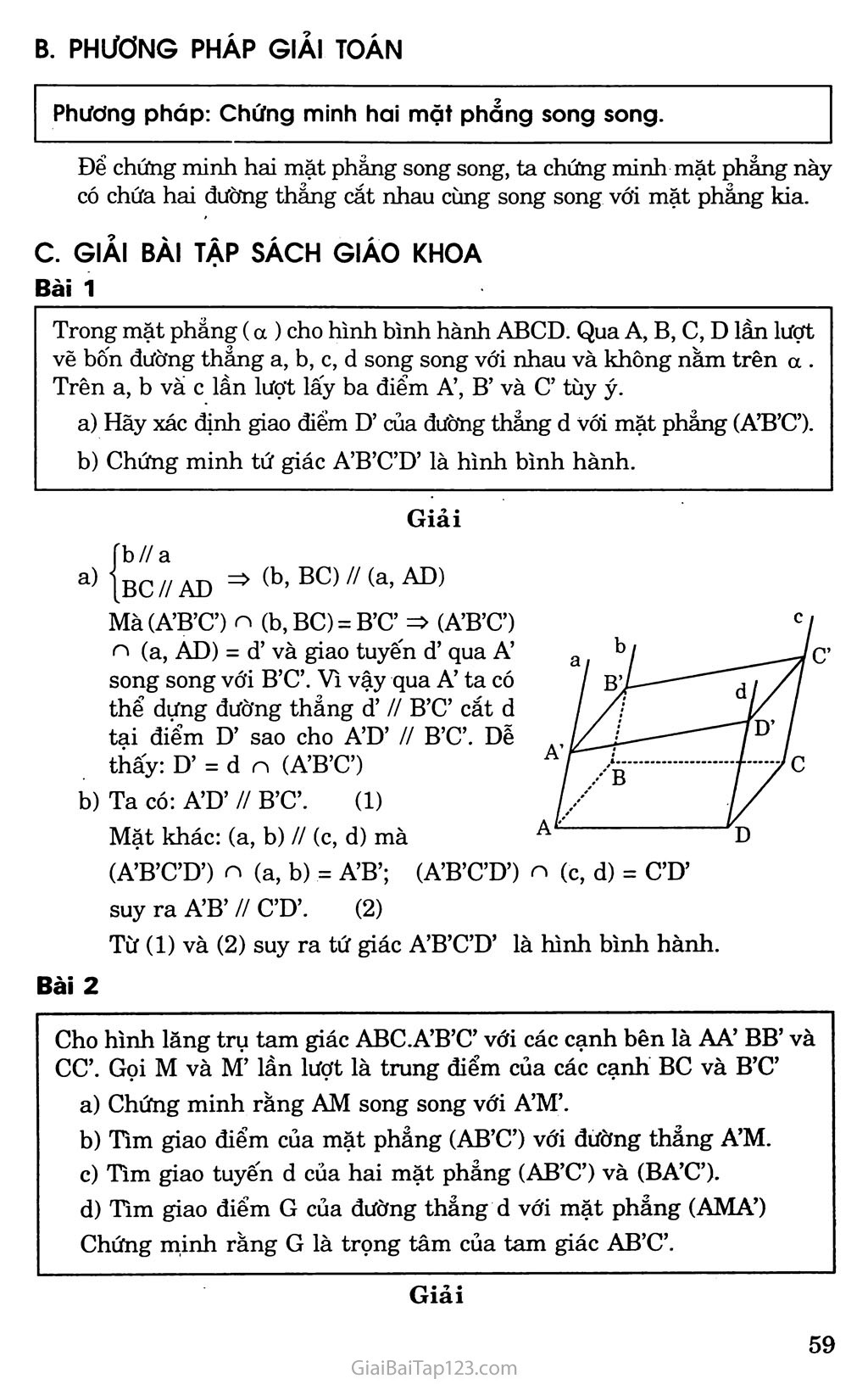
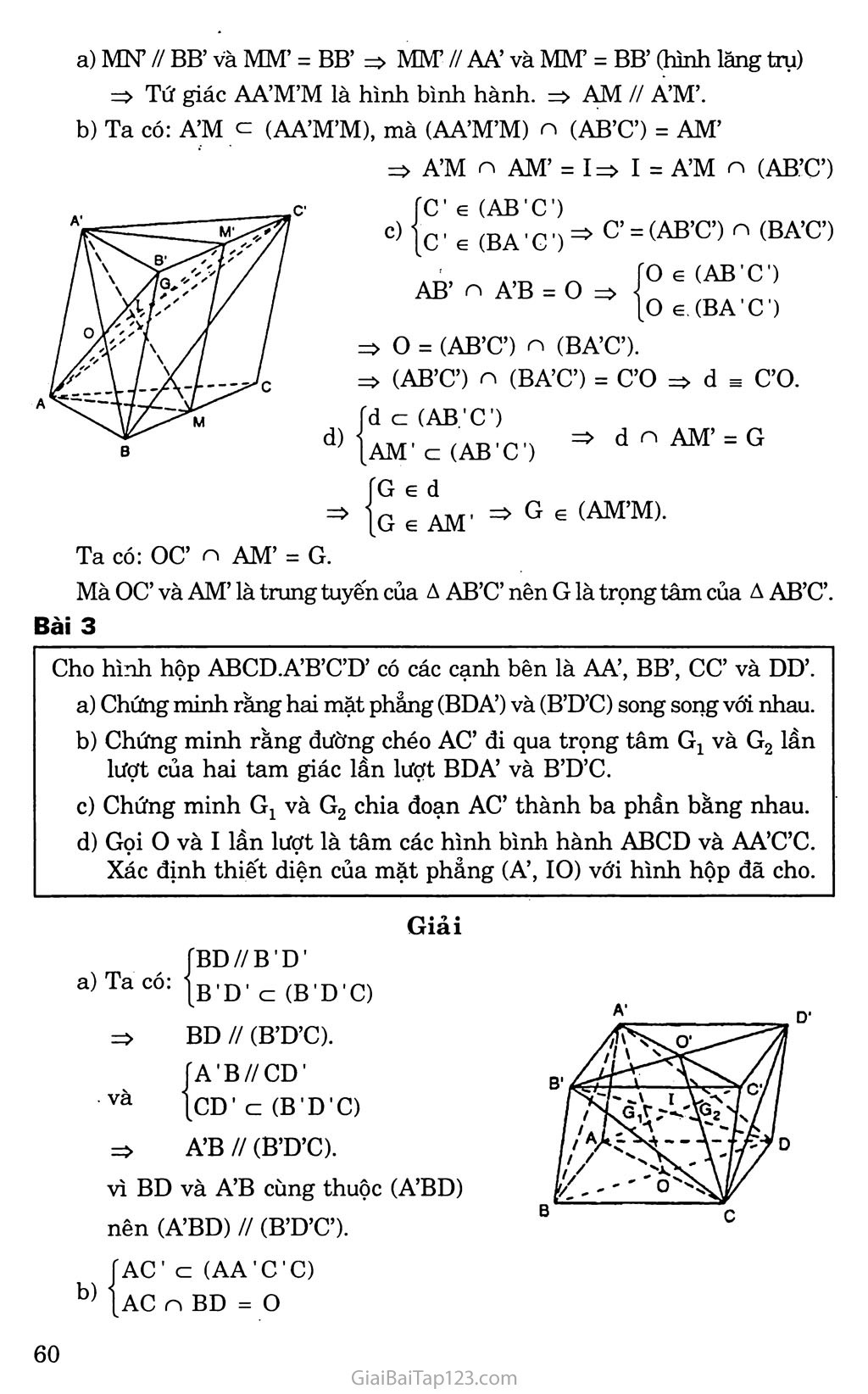
4)un đề 4. HAI MẶT PHẲNG SONG SONG
A. KIẾN THỨC CẦN NHỚ
I. ĐỊNH NGHĨA
Hai mặt phảng a và p được gọi là song song với nhau nếu chúng không có điểm chung, kí hiệu a // p hay p // a .
a//p a n p - 0
n ĐỊNH LÝ VÀ TÍNH CHAT
Nếu mặt phảng a chứa hai đường thẳng cắt nhau dp d2 và hai đường thẳng này cùng song song với mặt phảng p thì mặt phẳng a song song với mặt phảng p.
dj c a; d2 c a • dj n d2 = 0 => a // p
dj//p, d2//p
Chọ a và p là hai mặt phẳng song song với nhau. Nếu m'ặt phảngy cắt a theo giao tuyến d1 thì y cũng cắt p theo giao tuyến d2 và hai đường thẳng dj và d2 song song với nhau.
'a//p	fy n p = d2
7 n a = d,	|dj // d2
ra. ĐỊNH LÍ TA - LÉT (THALES)
Ba mặt phẳng song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
IV. HĨNH Ú TA - LÉT ĐẢO
Cho hai đường thẳng chéo nhau d và d’. Trên d và d’ lần lượt lấy A, B, c và A’, B’, C’ sao cho B nằm giữa A và c, B’ nằm giữa A’ và C’
AB BC vàA'B' " B'C'
Khi đó ba đường thảng AA’, BB’, CC’ lần lượt nằm trên ba mặt phảng song song với nhau.
B. PHƯƠNG PHÁP GIẢI TOÁN
Phương pháp: Chứng minh hai mặt phẳng song song.
Để chứng minh hai mặt phẳng song song, ta chúng minh mặt phẳng này có chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng kia.
c. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1	
Trong mặt phang (a ) cho hình bình hành ABCD. Qua A, B, c, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên a . Trên a, b vá c lần lượt lấy ba điểm A’, B’ và C’ tùy ý.
Hãy xác định giao điểm D’ của đường thẳng d vói mặt phẳng (A’B’C’).
Chúng minh tứ giác A’B’C’D’ là hình bình hành.
Giải
fb//a
|“c“ AD => (b, BC) // (a, AD)
Ma(A’B’C’) n (b,BC) = B’ơ => (A’B’Ơ) n (a, AD) = d’ và giao tuyến d’ qua A’ song song với B’C’. Vì vậy qua A’ ta có thể dựng đường thẳng d’ // B’C’ cắt d tại điểm D’ sao cho A’D’ // B’C’. Dễ thấy: D’ = d n (A’B’Ơ)
Ta có: A’D’ // B’C’.	(1)
Mặt khác: (a, b) // (c, d) mà
(A’B’C’D’) n (a, b) = A’B’;	(A’B’C’D’) n (c, d) = C’D’
suy ra A’B’ // C’D’ (2)
Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.
Bài 2
Cho hình lăng trụ tam giác ABC.A’B’C’ với các cạnh bên là AA’ BB’ và cơ. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’
Chứng minh rằng AM song song với A’M’.
Tìm giao điểm của mặt phẳng (AB’C’) với đứờng thẳng A’M.
Tìm giao tuyến d của hai mặt phảng (AB’Ơ) và (BA’C’h
Tìm giao điếm G của đường thẳng d với mặt phẳng (AMA’) Chứng minh rằng G là trọng tâm của tam giác AB’C’.
Giải
MN1 // BB’ và MM’ = BB’ => MM’ // AA’ và MM’ - BB’ (hình lăng trụ)
=> Tứ giác AA’M’M là hình bình hành. => AM // A’M’.
Ta có: A’M c (AA’M’M), mà (AA’M’M) n (AB’Ơ) = AM’
=> A’M n AM’ = I=> I = A’M n (AB’C’) fc’ e (AB'C)
o G (AB'C) o e.(BA’C')
o = (AB’Ơ) n (BA’Ơ).
:> (AB’Ơ) n (BA’Ơ) = C’O => d s C’O. d c (AB.'C)
AM' c (AB’C)
Ged
AB’ n A’B = o
d n AM’ = G
[c' e (BA 'C ’) => c’= (AB’Ơ) n (BA’Ơ)
1g e AM' => G G (A»
Ta có: OC’ n AM’ = G.
Mà OC’ và AM’ là trung tuyến của A AB’C’ nên G là trọng tâm của A AB’C’.
Bài 3
Cho hình hộp ABCD.A’B’C’D’ có các cạnh bên là AA’, BB’, CC’ và DD’.
Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song vói nhau.
Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác lần lượt BDA’ và B’D’C.
Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
Gọi o và I lần lượt là tâm các hình bình hành ABCD và AA’C’C. Xác định thiết diện của mặt phẳng (A’, 10) với hình hộp đã cho.
a) Ta có:
và
Giải
BD//B'D'
B'D' c (B’D’C)
BD // (B’D’C).
A'B//CD'
CD’ c (B'D’C)
b)
=> A’B // (B’D’C).
vì BD và A’B cùng thuộc (A’BD)
nên (A’BD) // (B’D’C).
AC' c (AA’C’C)
AC n BD = o
=} (AA’C’C) n (A’BD) = A’O
(Gj e (A’BD)
Gọi Gj = AC’ A A’O. Ta có e AC'
G,0 OA 1 AGlAO^ A G1C’A’ => Gj A* = A7 c= 2
Gj là trọng tâm của A A’BD.
Tương tự gọi G2 = AC’ n (B’D’C)
G2O' O’C’ 1 A G2O’C’ -V A G2CA =>	= I
=> G2 là trọng tâm của B’D’C.
, AG1 _ 1 AGj _ 1
Ta có G C, 2 => AC, - 3 .
Tương tự
Suy ra	=
1	C'G2 = 1
~ 2	C'A 3
— => AGj = GjG2 = G2C’.
(ATO)- (AA’C’C) => (AĨO) cắt hình hộp đã cho theo thiết diện là hình bình hành AA’C’C.
Bài 4
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ // BB’ // CC’. Gọi H là trung điểm của cạnh A’B’.
Chứng minh rằng đường thẳng B’C song song với mặt phẳng (AHƠ)
Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (A’BC). Chứng minh rằng d song song với mặt phảng (BB’C’C).
Xác định thiết diện của mặt phảng (H, d) với hình lăng trụ ABC.A’B’C đã cho.
Giải
Gọi o = AC’ n A’C
Ta có HO // B’C (HO là đường trung bình A A’B’C) và HO c (AHƠ) => B’C // (AHC’)
Ta có A’C n AC’= o
rOe(A’BC)
=> [Oe(AB'C')
=> o = (A’BC) (AB’C’)
V T _ A I'D _ A R’ ■ f 1 e 1A BC) và gọi I = A B n AB	i
[Ie(AB’C')
=> I = (A’BC) n (AB’C’)
=> (A’BC) n (AB’C’) = 01 Vậy 01 = d.
Ta CÓ 01 // B’C’ (đường trung bình A AB’C Mà B’C’ c (BB’C’C) => 10 // (BB’C’C)
Gọi HN = (HI0)n (A’B’C’) (N e A’C’).
Vi IO // (A’B’C’) nên HN // B’C’.
Gọi KM = (HIO) n (ABC) (M 6 AC, K ey nên KM // IO.
Theo b) ta CÓ IO // B’C’ nên KM // HN.
Ta CÓ HI // AA => (HIO) // AA.
Mà AA = (AA’C’C) n (AA’B’B), (HIO) n (AA’C’C) = MN,
(HIO) n (AA’B’B) = HK, suy ra MN // AA và HK //AA’ MN // HK.(2) Từ (1) và (2) suy ra thiết diện cần tìm là hình bình hành MNHK.
D. BÀI TẬP ĐỀ NGHỊ
Bài 1
Cho tứ diện ABCD. Gọi M là trung điểm của AB. Hỏi mặt phẳng (P) qua điểm M và song song với tất cả AD và BC có đi qua trung điểm N của CD hay không? Tại sao?
Bài 2
Cho hai điểm M, N lần lượt thay đổi trên mặt phảng song song (P) và (Q). Tìm tập hợp điểm I thuộc đoạn thẳng MN sao cho	= k (* 0) cho trước.
Bài 3
Cho hình lăng trụ tam giác ABCA’B’C’. Gọi H là trung điểm của cạnh AB’.
Chứng minh rằng đường thẳng CB’ song song với mp(AHC’).
Tìm giao tuyến d của hai mặt phắng (AB’C’) và (ABC). Chứng minh rằng d song song với mp(BB’C’C).
Xác định thiết diện của hình lăng trụ ABC.A’B’C’ khi cắt bỏi mp(H, d).
Bài 4
Cho hình hộp ABCD.A’B’C’D’.
Chứng minh rằng mp(BDA) // mp(B’D’C)
Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1; G2 của hai tam giác BDA’ và B’D’C.
Chứng minh rằng Gi và G2 chia đoạn AC’ thành ba phần bằng nhau.
Gọi I, K lần lượt là tâm của hình bình hành ABCD và BCC’B’. Xác định thiết diện của hình đã cho cắt bởi mp(AIK).