Giải Toán 11: Vấn đề 5. Khoảng cách

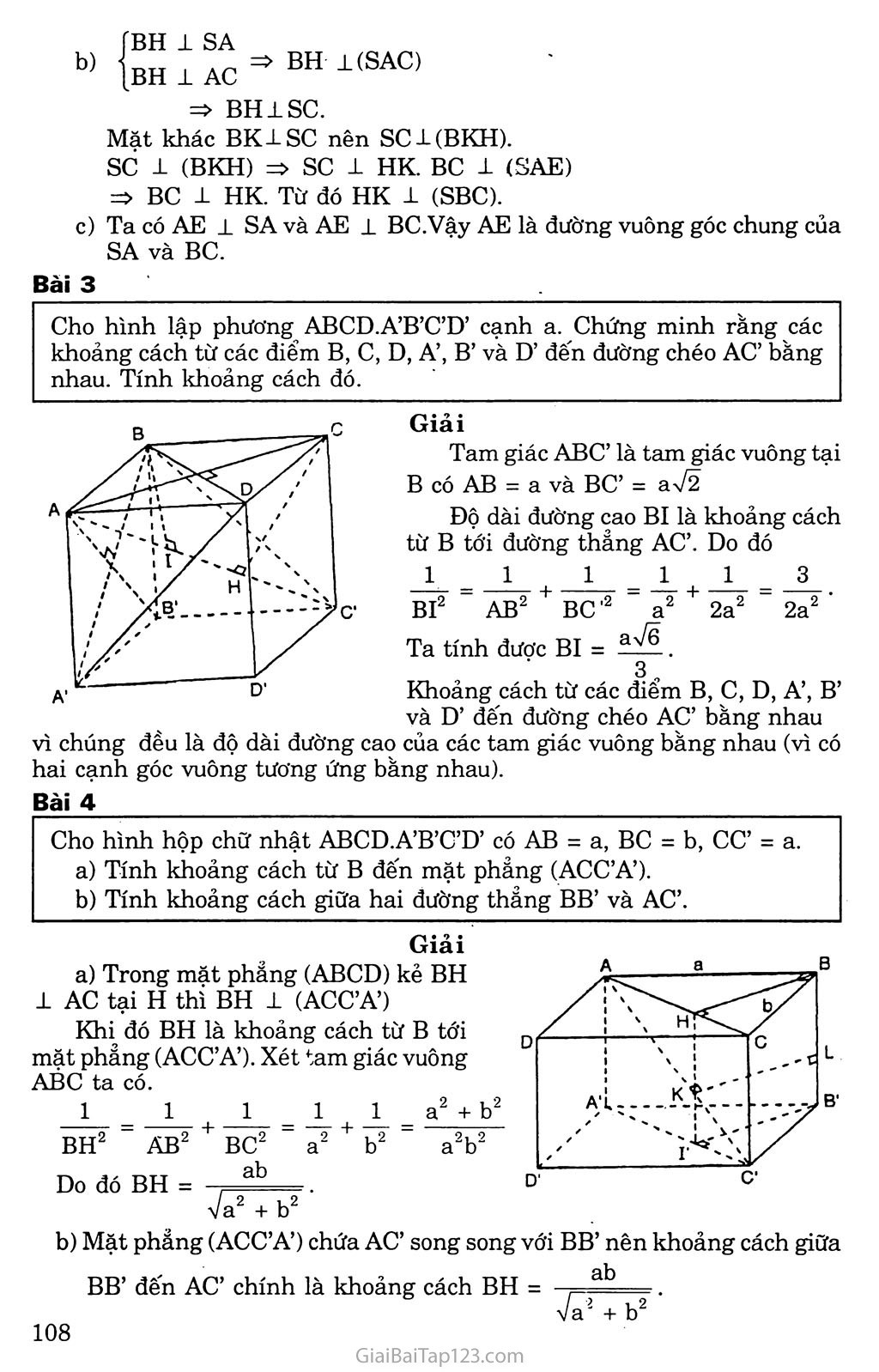
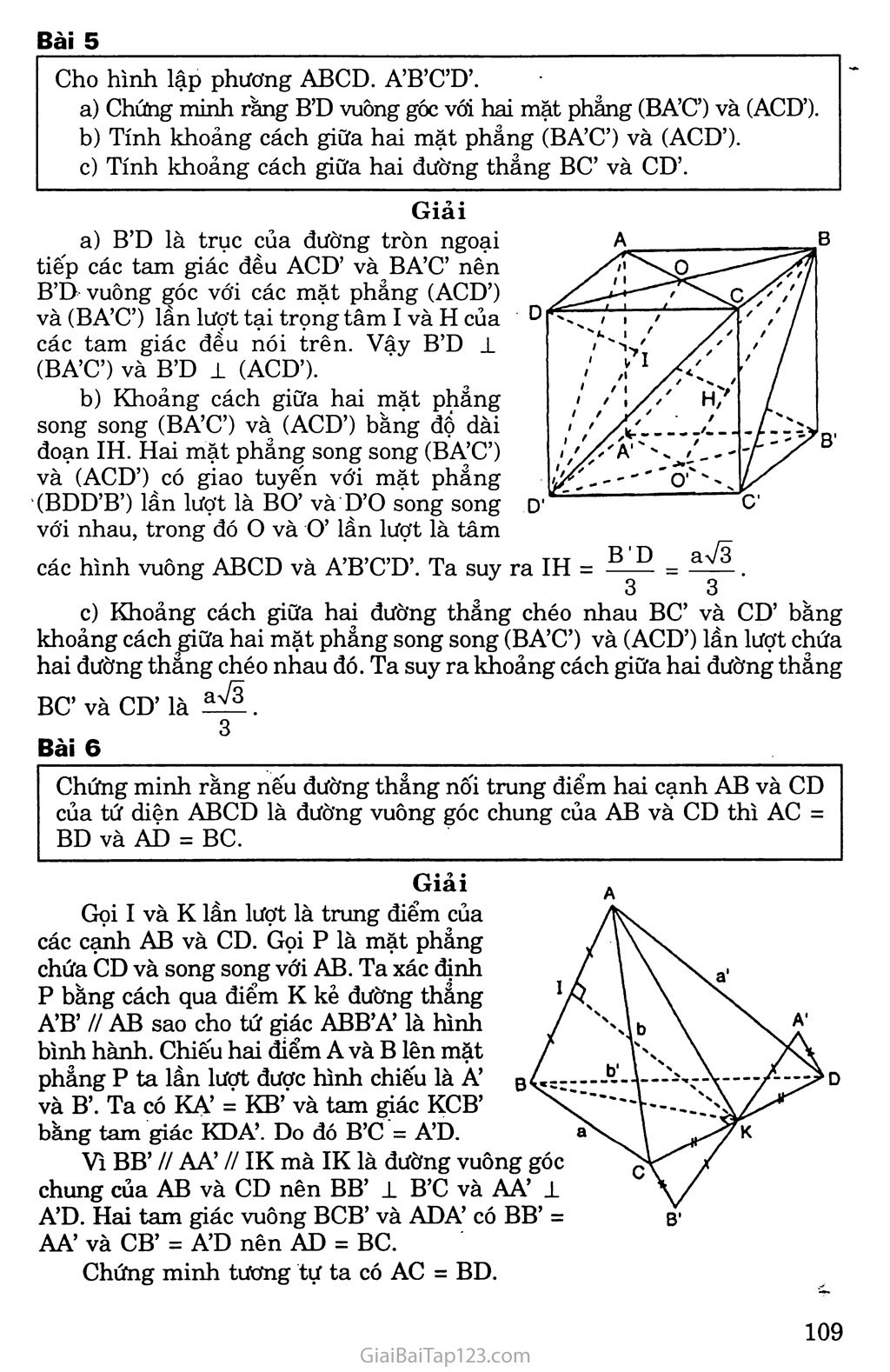
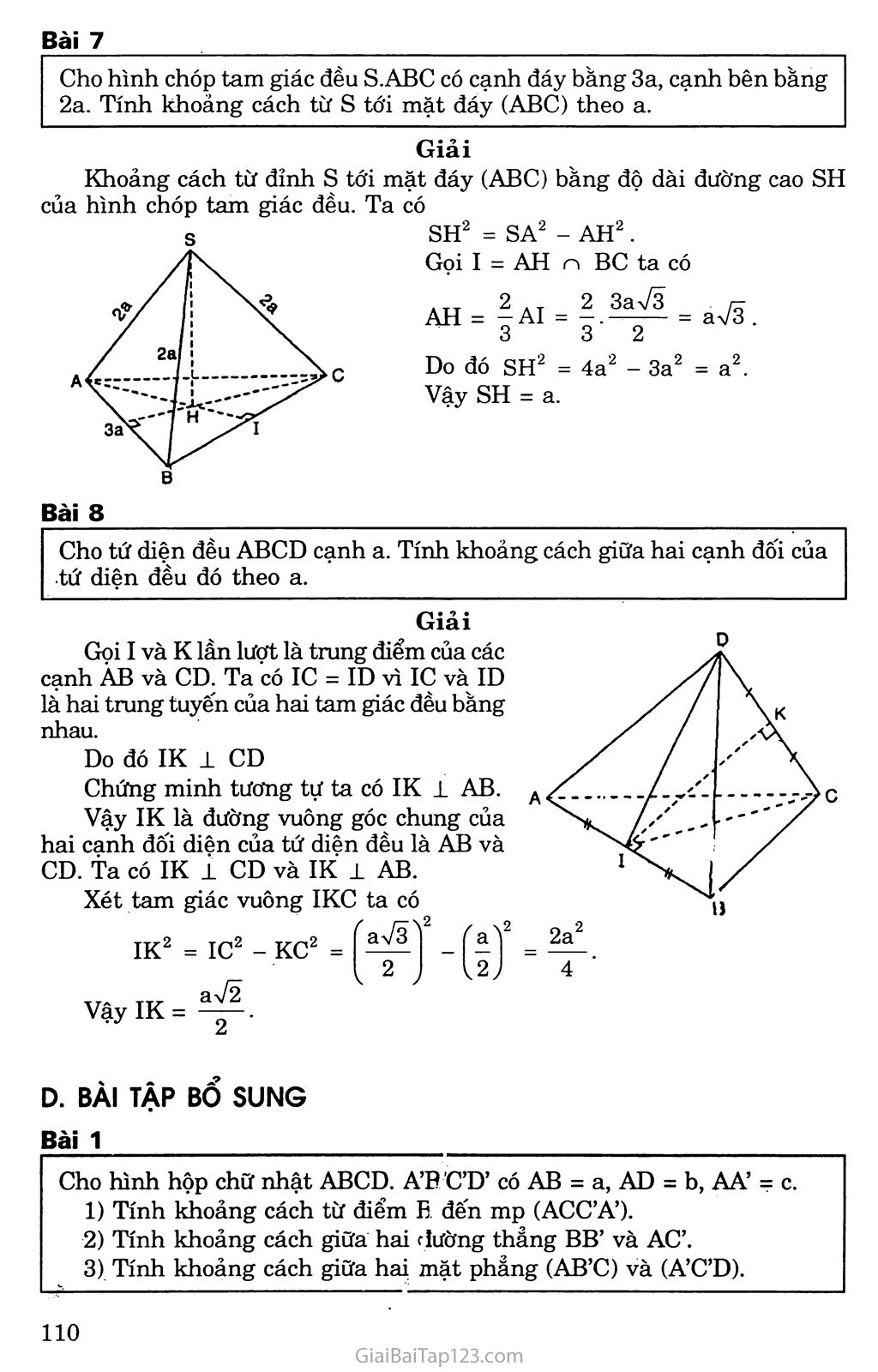
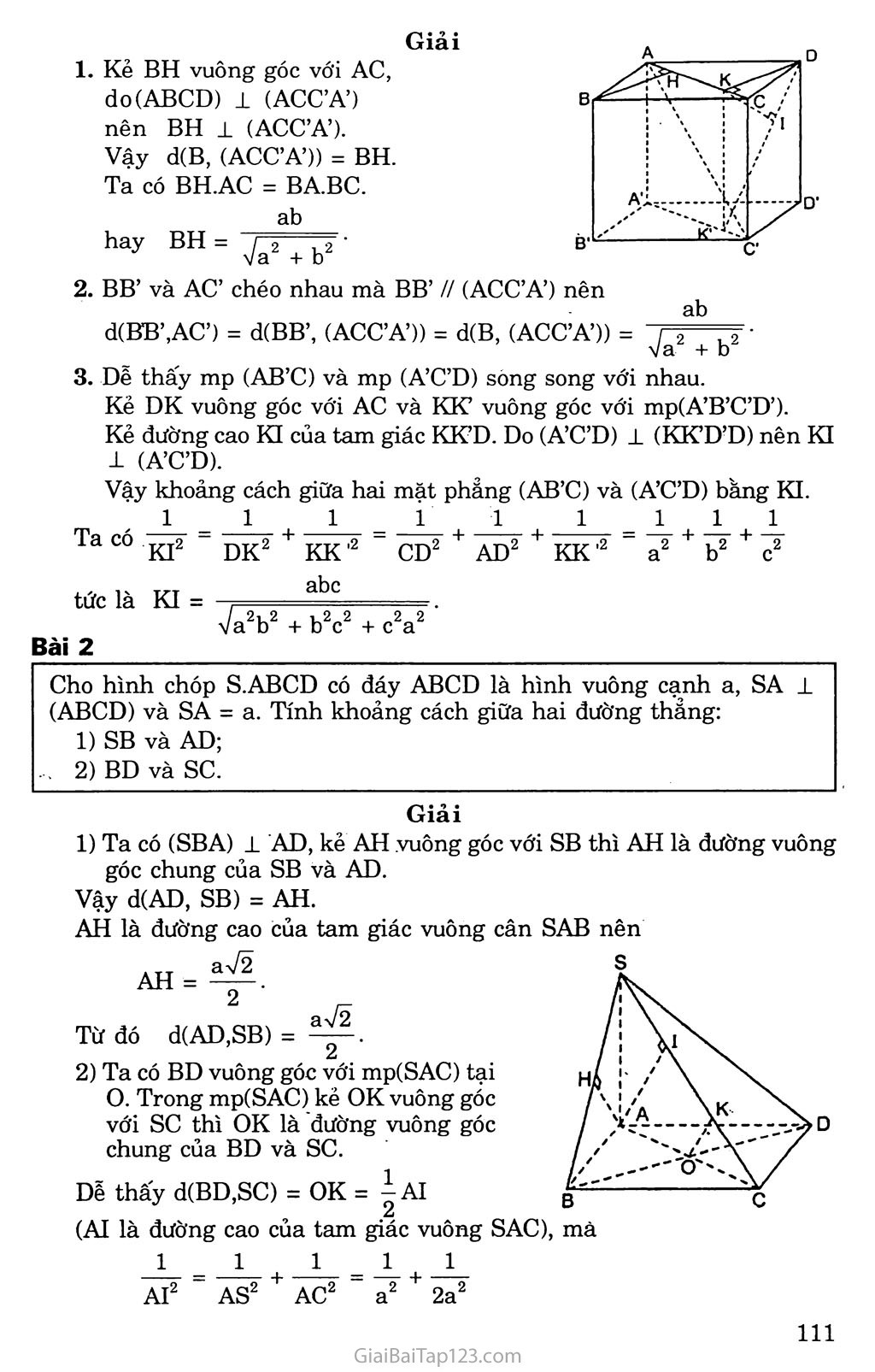
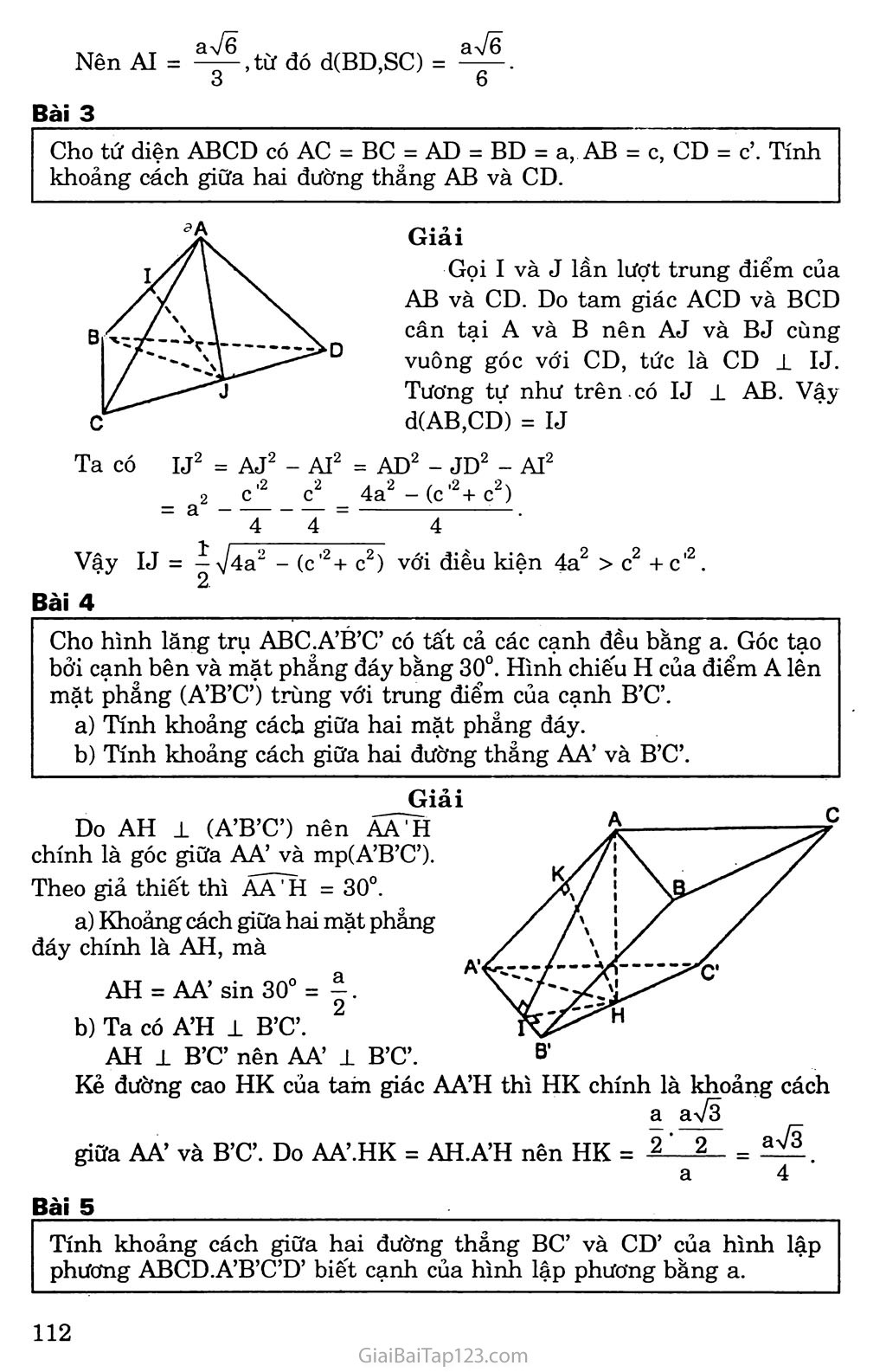
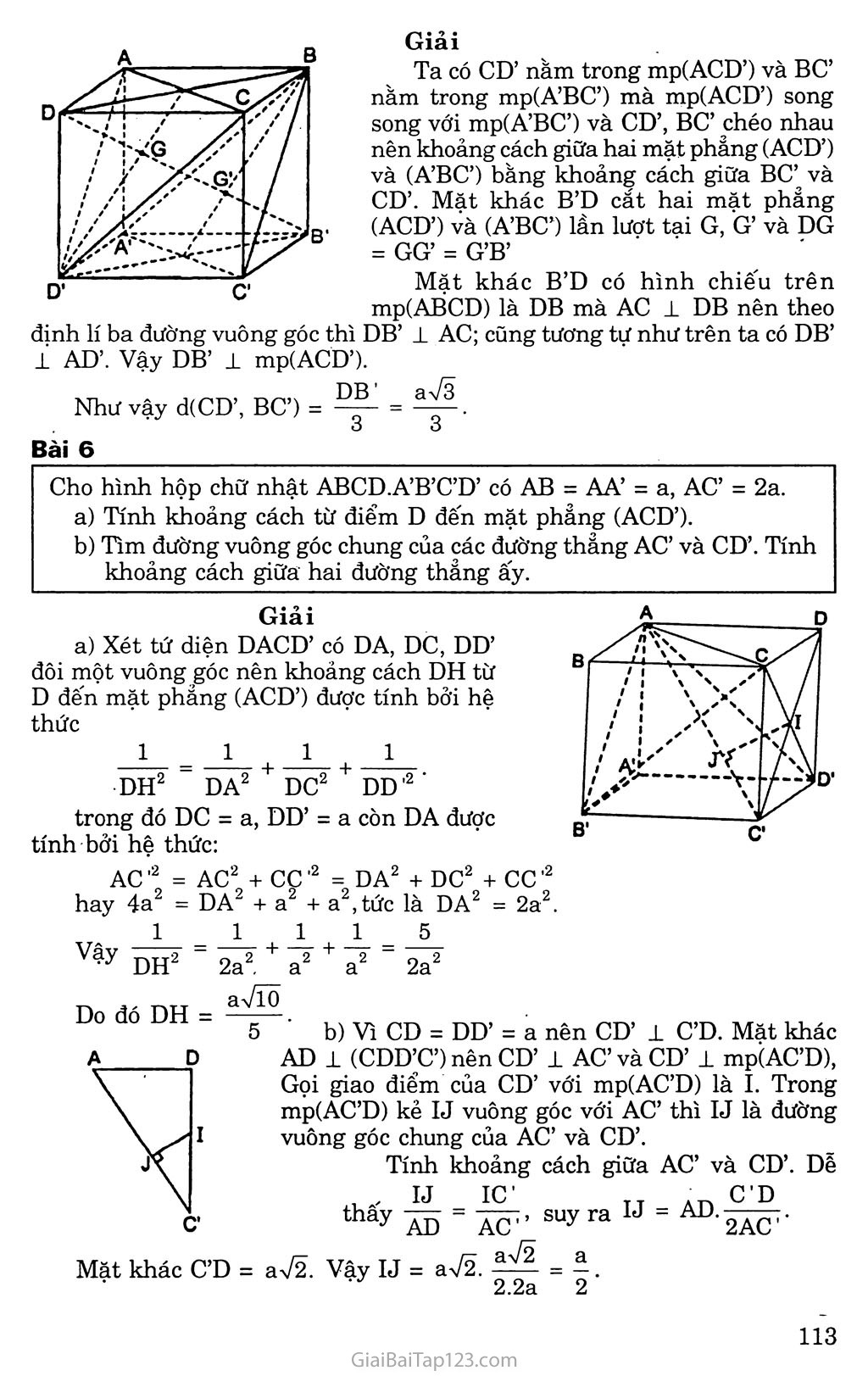
k. KIẾN THỨC CẦN NHỚ
Khoảng cách từ một điểm o đến đường thẳng a là độ dài đoạn OH -L a với H G a, kí hiệu là d(O, a). Chú ý: d(O, a) =OH ắ OM với mọi M e a.
Khoảng cách từ một điểm o đến mặt phẳng a là độ dài đoạn OH 1 a với H e a , kí hiệu d(O, a ). Chú ý: d(O, ct) = OH ắ OM với mọi M e a .
Khoảng cách giữa giữa đường thẳng a và mặt phẳng a song song với a là khoảng cách từ một điểm A bất kì thuộc a tới mặt phang a .
Kí hiệu d(a, a ) = d(A, a ) với Ae a
Khoảng cách giữa hai mặt phẳng song song a và p là khoảng cách từ một điếm M bất kì' trên mặt phẳng này đến mặt phẳng kia.
Kí hiệu d( a , p) = d(M, p ) với M 6 a
d( a , p) = d(N, a ) với N e p
Khoảng cách giữa hai đường thẳng chéo nhau là độ dài của đoạn vuông góc chung giữa hai đường thẳng đó.
B. PHƯƠNG PHÁP GIẢI TOÁN
CÁCH TÍNH KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THANG CHÉO NHAU
Ta có các trường hợp sau đây:
Giả sử a và b là hai đường thẳng chéo nhau vàa i b. Ta dựng mặt phẳng a chứa a và vuông góc với b tại B. Trong a dựng BA ± a tại A, ta được độ dài đoạn BA là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Giả sử a và b là hai đường thẳng chéo nhau.
Ta dựng mặt phẳng a chứa a và song song với b
Lấy một điểm M tùy ý trên b dựng MM’ 1 a tại M’
Từ M’ dựng b’ // b cắt a tại A
Từ A dựng AB // MM’ cắt b tại B độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Giả sử a và b là hai đường thẳng chéo nhau.
Ta dựng mặt phảng a 1 a tại o, a cắt b tại I.
Dựng hình chiếu vuông góc của b là b’ trên a
Trong mặt phẳng a , vẽ OH J-b’
Từ H dựng đường thẳng song song với a cắt b tại B
Từ B dựng đường thẳng song song với OH cắt a tại A
Độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1
Trong các mệnh đề sau đây, mệnh đề nào đúng, mệnh đề nào sai?
Đường thẳng A là đường vuông góc chung của hai đường thẳng a và b nếu A la và A 1 b.
Nếu p là mặt phẳng song song với cả hai đường thẳng a và b chéo nhau thì đường vuông góc chung của a và b luôn luôn vuông góc với p.
Nếu A là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì A là giao tuyến của hai mặt phắng (a, A) và (b, A ).
Cho hai đường thẳng chéo nhau a và b. Đường thẳng đi qua một điểm trên a đồng thời cắt b và vuông góc với b là đường vuông góc chung của a và b.
Đường vuông góc chung của hai đường thẳng chéo nhau nằm trong mặt phảng chứa đường này và vuông góc với đường kia.
Trả lời
Sai	b) Đúng c) Đúng d) Sai e) Sai.
Bài 2	 	
Cho tứ diện S.ABCD có SA vuông góc với mặt phẳng (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Chứng minh ba đường thẳng AH, SK và BC đồng quy.
Chứng minh rằng SC±(BHK) và HK±(SBC).
Xác định đường vuông góc chung của BC và SA.
Giải
Gọi E = AHnBC
Ta có SA ± (ABC) SA ± BC. SA 1 (SAE) => BC 1 AH
và BC 1 SA,
suy ra BC ± (SAH) => BC ± SE. Ta suy ra ba đường thẳng AH, SK và BC đồng quy.
fBH ± SA
[BH I AC =* BH 1 (SAC)
=> BH±SC.
Mặt khác BK1SC nên SCl(BKH). sc 1 (BKH) SC 1 HK. BC 1 (SAE)
=> BC ± HK. Từ đó HK 1 (SBC).
Ta có AE ± SA và AE 1 BC.Vậy AE là đường vuông góc chung của SA và BC.
Bài 3
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, c, D, A’, B’ va D’ đến đường chéo AC’bằng nhau. Tính khoảng cách đó.
vì chúng đều là độ dài đường c hai cạnh góc vuông tương ứng
Giải
Tam giác ABC’ là tam giác vuông tại B có AB = a và BC’ = a\/2
Độ dài đường cao BI là khoảng cách từ B tới đường thảng AC’. Do đó
1 =	1	1	113
BI2 " AB2 + BC’2 "a2 + 2a2 " 2a2 ’
Ta tính được BI=
,	/, - , 5
Khoảng cách từ các điểm B, c, D, A’, B’ và D’ đến đường chéo AC’ bằng nhau của các tam giác vuông bằng nhau (vì có ng nhau).
Bài 4	
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = a.
Tính khoảng cách từ B đến mặt phảng (ACC’A’).
Tính khoảng cách giữa hai đường thẳng BB’ và AC’.
Giải
a) Trong mặt phẳng (ABCD) kẻ BH 1 AC tại H thi BH 1 (ACC’A’)
Khi đó BH là khoảng cách từ B tới mặt phảng (ACC’A’). Xét tam giác vuông ABC ta có.
1 = 1	1 = 1 2_ _ a2 + 1)2
BH2 - AB2 + BC2 - a2 + b2 - a2b2 ah
Do đó BH =	,	- ■
Va2 + b2
Mặt phẳng (ACC’A’) chứa AC’ song song với BB’ nên khoảng cách giữa BB’ đến AC’ chính là khoảng cách BH = ab
v?+b2
Bài 5
Cho hình lập phương ABCD. A’B’C’D’.
Chứng minh rằng B’D vuông góc với hai mặt phẳng (BA’C’) và (ACD’).
Tính khoảng cách giữa hai mặt phẳng (BA’Ơ) và (ACD’).
Tính khoảng cách giữa hai đường thẳng BC’ và CD’.
Giải
/ít Ị
''' ' / / ! '"'ó s''
'	' y /'	n,
• • 7/ ■	'
/ ' /
/ /
/ / t Ị
/ Ị
, '/,'ù
/	X
0'
"I	/
B'
B'D _ aVÕ
B’D là trục của đường tròn ngoại tiếp các tam giác đều ACD’ và BA’C’ nên B’D vuông góc với các mặt phẳng (ACD’) và (BA’Ơ) lần lượt tại trọng tâm I và H của các tam giác đều nói trên. Vậy B’D 1 (BA’Ơ) và B’D 1 (ACD’).
Khoảng cách giữa hai mặt phẳng song song (BA’C’) và (ACD’) bằng đọ dài đoạn IH. Hai mặt phẳng song song (BA’C’) và (ACD’) có giao tuyến với mặt phẳng (BDD’B’) lần lượt là BO’ và D’O song song với nhau, trong đó o và O’ lần lượt là tâm các hình vuông ABCD và A’B’C’D’. Ta suy ra IH =
Khoảng cách giữa hai đường thẳng chéo nhau BC’ và CD’ bằng khoảng cách giữa hai mặt phảng song song (BA’Ơ) và (ACD’) lần lượt chứa hai đường thẳng chéo nhau đó. Ta suy ra khoảng cách giữa hai đường thẳng
BC’ và CD’ là .
3
Bài 6	
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AỈ) = BC.
Giải
Gọi I và K lần lượt là trung điểm của các cạnh AB và CD. Gọi p là mặt phảng chứa CD và song song với AB. Ta xác định p bằng cách qua điểm K kẻ đường thảng A’B’ // AB sao cho tứ giác ABB’A’ là hình bình hành. Chiếu hai điểm A và B lên mặt phẳng p ta lần lượt được hình chiếu là À’ và B’. Ta có KẠ’ = KB’ và tam giác KCB’ bằng tam giác KDA’. Do đó B’C = A’D.
Vì BB’ // AA’ // IK mà IK là đường vuông góc chung của AB và CD nên BB’ 1 B’C và AA’ 1 A’D. Hai tam giác vuông BCB’ và ADA’ có BB’ = AA’ và CB’ = A’D nên AD = BC.
Chứng minh tương tự ta có AC = BD.
Bài 7
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ s tới mặt đáy (ABC) theo a.
Giải
SH2 = SA2 - AH2,
Khoảng cách từ đỉnh s tới mặt đáy (ABC) bằng độ dài đường cao SH của hình chóp tam giác đều. Ta có
Gọi I = AH n BC ta có
ATT 2 AT 2 3aV3	r-
AH = 77 AI = 77 ■	= ay 3 .
3	3	2
Do đó SH2 = 4a2 - 3a2 = a2. Vậy SH = a.
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối của tứ diện đều đó theo a.
4
Giải
Gọi I và K lần lượt là trung điểm của các cạnh ÀB và CD. Ta có IC = ID vì IC và ID là hai trung tuyến của hai tam giác đều bằng nhau.
Do đó IK 1 CD
Chứng minh tương tự ta có IK 1 AB.
Vậy IK là đường vuông góc chung của hai cạnh đối diện của tứ diện đều là AB và CD. ta có IK 1 CD và IK ± AB.
Xét tam giác vuông IKC ta có
IK2 = IC2 - KC2 =
" 
VậyIK=^.
J 2
D. BÀI TẬP BỔ SUNG
Bài 1
Cho hình hộp chữ nhật ABCD. A’B C’D’ có AB = a, AD = b, AA’ = c.
Tính khoảng cách từ điểm H đến mp (ACC’A’).
Tính khoảng cách giữa hai đường thẳng BB’ và AC’.
Tính khoảng cách giữa hai mặt phẳng (AB’C) và (A’C’D).
Kẻ BH vuông góc với AC,
do(ABCD) 1 (ACC’A’)
nên BH 1 (ACC’A’).
Vậy d(B, (ACC’A’)) = BH.
Ta có BH.AC = BA.BC.
ab
hay BH = / 2	2 •
yja + b
Giải
7‘
ỉ '
1	\	ỉ
•
*	\ i
ì	' ■
\ ỉ .
A’i	
X
A
BB’ và AC’ chéo nhau mà BB’ // (ACC’A’) nên
ab
d(BB’,AC’) = d(BB’, (ACC’A’)) = d(B, (ACC’A’)) = <2	c?-
va + b
Dễ thấy mp (AB’C) và mp (A’C’D) song song với nhau.
Kẻ DK vuông góc với AC và KK’ vuông góc với mp(A’B’C’D’).
Kẻ đường cao KI của tam giác KK’D. Do (A’C’D) 1 (KK’D’D) nên KI
± (A’C’D).
Vậy khoảng cách giữa hai mặt phẳng (AB’C) và (A’C’D) bằng KI.
11 1 11 1111
Ta có
KI DK
tức là KI =
Bài 2
KK'
abc
CD AD
KK
.2 + „2 b c
/_ 2i_2	,22	2	2	'
va b + b c + c a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ± (ABCD) và SA = a. Tính khoảng cách giữa hai đường thẳng:
1) SB và AD;
. 2) BD và SC.
Giải
1) Ta có (SBA) 1 AD, kẻ AH vuông góc với SB thì AH là đường vuông
góc chung của SB và AD.
Vậy d(AD, SB) = AH.
AH là đường cao của tam giác vuông cân SAB nên
a 72
AH =
ỉ 72
Từ đó d(AD,SB) =
2) Ta có BD vuông góc với mp(SAC) tại
o. Trong mp(SAC) kẻ OK vuông góc
với sc thì OK là đường vuông góc
chung của BD và sc.
Dễ thấy d(BD,SC) = OK = |aI
(AI là đường cao của tam giác vuông SAC), mà
1 1.1
t2
AI
AS AC
1 1 a2 + 2a2
Nên AI = ^Ltừ đó d(BD,SC) =
3	6
Bài 3	
Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.
Giải
Gọi I và J lần lượt trung điểm của AB và CD. Do tam giác ACD và BCD cân tại A và B nên AJ và BJ cùng vuông góc với CD, tức là CD 1 IJ. Tương tự như trên có IJ ± AB. Vậy d(AB,CD) = IJ
= AD2 - JD2 - AI2
4a2 - (c'2+ c2)
4
Bài 4
Vậy IJ = í ự4a2 - (c,2+ c2) với điều kiện 4a2 > c2 + c'2. 2-
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30°. Hình chiếu H của điểm A lên mặt phảng (A’B’Ơ) trùng với trung điểm của cạnh B’ơ.
Tính khoảng cách giữa hai mặt phẳng đáy.
Tính khoảng cách giữa hai đường thẳng AA’ và B’C’.
Do AH 1 (A’B’C’) nên AA'H chính là góc giữa AA’ và mp(A’B’C’).
Theo giả thiết thì AA' H = 30°.
Khoảng cách giữa hai mặt phẳng đáy chính là AH, mà
AH = AA’ sin 30° = ệ.
Ta có A’H 1 B’C’.
AH 1 B’C’ nên AA’ 1 B’C’.
Kẻ đường cao HK của tam giác AA’H thì HK chính là khoảng cách a a 73
giữa AA’ và B’C’. Do AA’.HK = AH.A’H nên HK =	= ^1.
a	4
Bài 5	
Tính khoảng cách giữa hai đường thẳng BC’ và CD’ của hình lập phương ABCD.A’B’C’D’ biết cạnh của hình lập phương bằng a.
Giải
Ta có CD’ nằm trong mp(ACD’) và BC’ nằm trong mp(A’BC’) mà mp(ACD’) song song với mp(A’BC’) và CD’, BC’ chéo nhau nên khoảng cách giữa hai mặt phẳng (ACD’) và (ABC’) bằng khoảng cách giữa BC’ và CD’. Mặt khác B’D cắt hai mặt phẳng (ACD’) và (ABC’) lần lượt tại G, G’ và DG = GG’ = G’B’
Mặt khác B’D có hình chiếu trên mp(ABCD) là DB mà AC 1 DB nên theo
định lí ba đường vuông góc thì DB’ ± AC; cũng tương tự như trên ta có DB’ i Aơ. Vậy DB’ 1 mp(ACD’).
Như vậy d(CƠ, Bơ) =^~ =
Bài 6
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a, AC’ = 2a.
Tính khoảng cách từ điểm D đến mặt phảng (ACD’).
Tìm đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng cách giữa hai đường thẳng ấy.
//
/
D X—	L
/ỷ
\ 'S
\	X \
''
'' rĩ -	
\
Al
</ \
\ / \
/ \ \
T~J^D
B'
c*
Giải
Xét tứ diện DACD’ có DA, DC, DD’ đôi một vuông góc nên khoảng cách DH từ D đến mặt phẳng (ACD’) được tính bởi hệ thức
1 _ 1 1 1
DH2 ” DA2 + DC2 + DD'2 ■
AC ,2_ = AC2. + cc '2
DA2 + DC2 + cc 2a!
trong đó DC = a, DD’ = a còn DA được tính bởi hệ thức:
2a
hay 4a = DA + a + a , tức là DA
2a a a aVĨÕ
5	' b) Vì CD = DD’ = a nên CD’ 1 C’D. Mặt khác
AD 1 (CDƠƠ) nên CD’ 1 AC’ và cơ 1 mp(AC’D), Gọi giao điểm của CD’ với mp(AC’D) là I. Trong mp(AƠD) kẻ IJ vuông góc với AC’ thì IJ là đường vuông góc chung của AC’ và CD’.
Tính khoảng cách giữa AC’ và CD’. Dễ
thỉy AD ’ AC’’ suy ra “ 2AC'
Mặt khác C'D = aựỉ. Vậy IJ = aVã. iA .	.
•	J	2.2a	2
Bài 7
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có cạnh SA vuông góc với mặt phảng (ABCD) và SA = a. Tính khoảng cách giữa hai đường thằng chéo nhau sc và BD.
Giải
Gọi o là tâm cùa hình vuông ABCD.
Trong mặt phẳng SAC vẽ OH vuông góc với SC (H e SC)
Ta có:
ÍBD 1 AC
BD ± SA => BD 1 (SAC) => BD 1 OH.
Mặt khác OH ± sc. Vậy OH là đoạn vuông góc chung của sc và BD.
Ta có OH chính là khoảng cách giữa hai đường thẳng chéo nhau sc và BD.
Hai tam giác vuông SAC và OHC đồng dạng vì có chung góc nhọn c.
SA OH,	.
Do đó gc = Õẽ (= sin C).'
~ SA.OC Vay H-	.
Ta có SA = a, oc =	, sc = VsA2 + AC2 = ya2 + 2a2 = aVã.
aV2-
a.	aựg
Vậy OH - 	= ——— hay khoảng cách giữa hai đường thảng chéo
aV3 6
nhau sc và BD là ^ệ-.
6
E. BÀI TẬP ĐỀ NGHỊ
Bài 1
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Các cạnh bên SA = SB = SC = SD = a 72. Gọi I và K lần lượt là trung điểm của AD và BC.
Chứng minh mặt phảng (SIK) vuông góc với mặt phẳng (SBC).
Tính khoảng cách giữa hai đường thẳng AD và SB.
Bài 2
Cho hình lập phương ABCD.A’B’C’D’.
Chứng minh đường thẳng BC’ vuông góc với mặt phẳng (A’B’CD).
Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’.
Bài 3
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy (ABCD) với SA = aVẽ.
Tính các khoảng cách từ A và B đến mặt phẳng (SCD).
Tính khoảng cách từ đường thẳng AD đến mặt phảng (SBC).
Bài 4
Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng AC = BC = AD = BD = a và AB = p, CD = q.
Bài 5
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
Tính khoảng cách từ s tới mặt phẳng đáy (ABC).
Tính khoảng cách giữa hai đường thẳng AB và SG.
Bài 6
Cho hình lăng trụ tam giác có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phảng đáy góc 60° và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A’B’Ơ) trùng với trung điểm của cạnh B’C’.
Tính khoảng cách giữa hai mặt phảng đáy.
Chứng minh rằng mặt bên BCC’B’ là một hình vuông.