Giải Toán 11: Vấn đề 1. Vectơ trong không gian
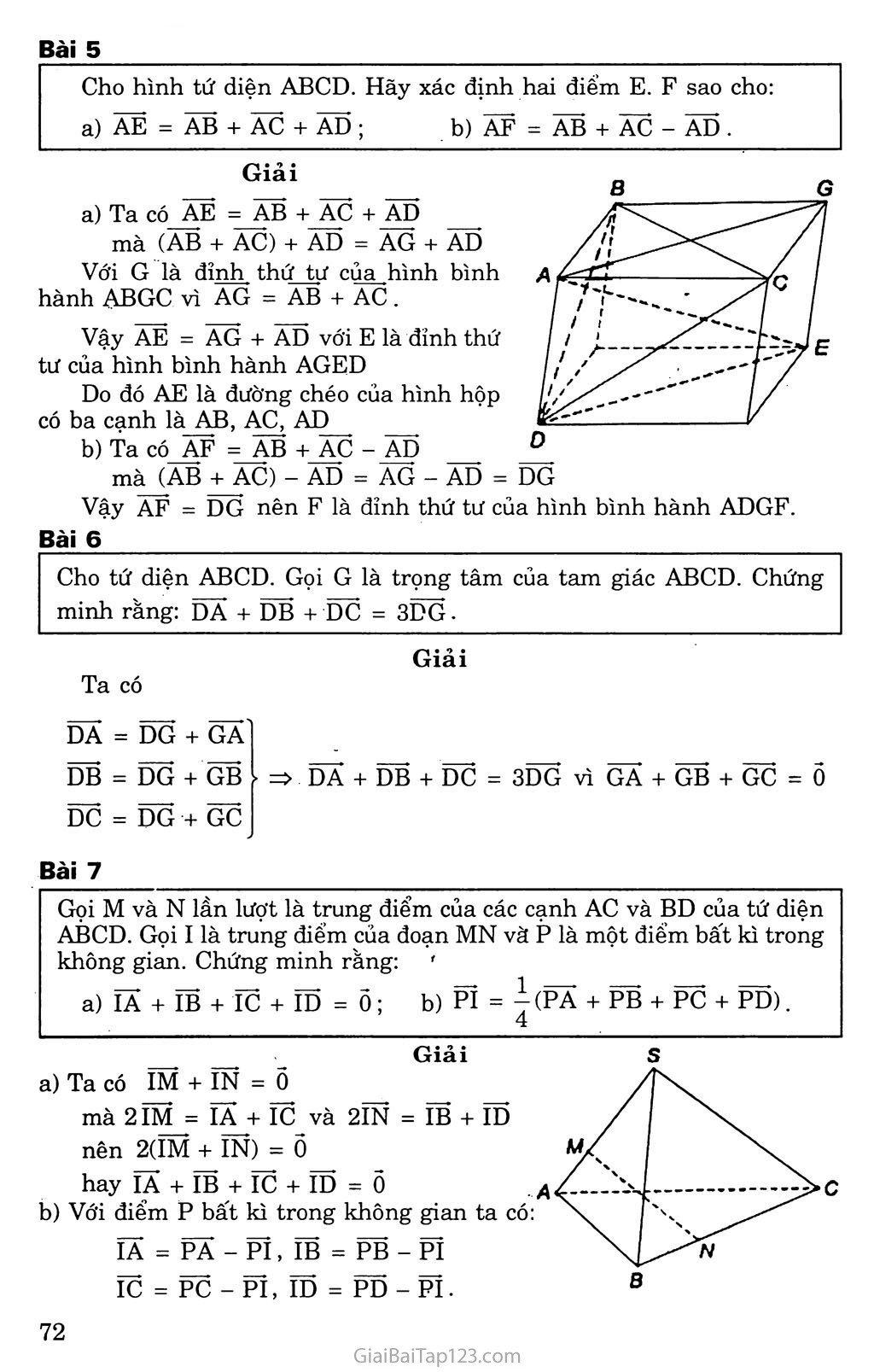
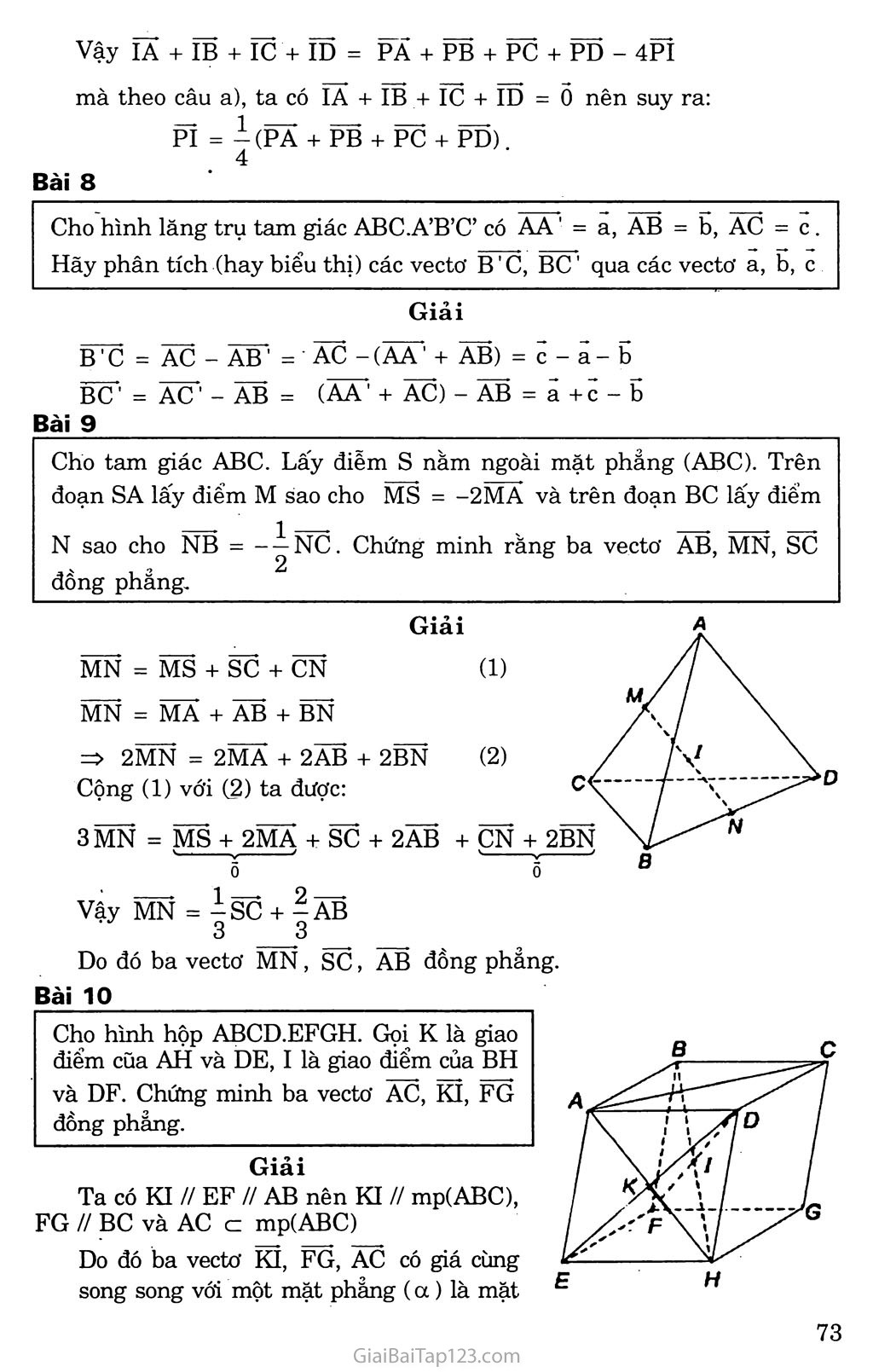
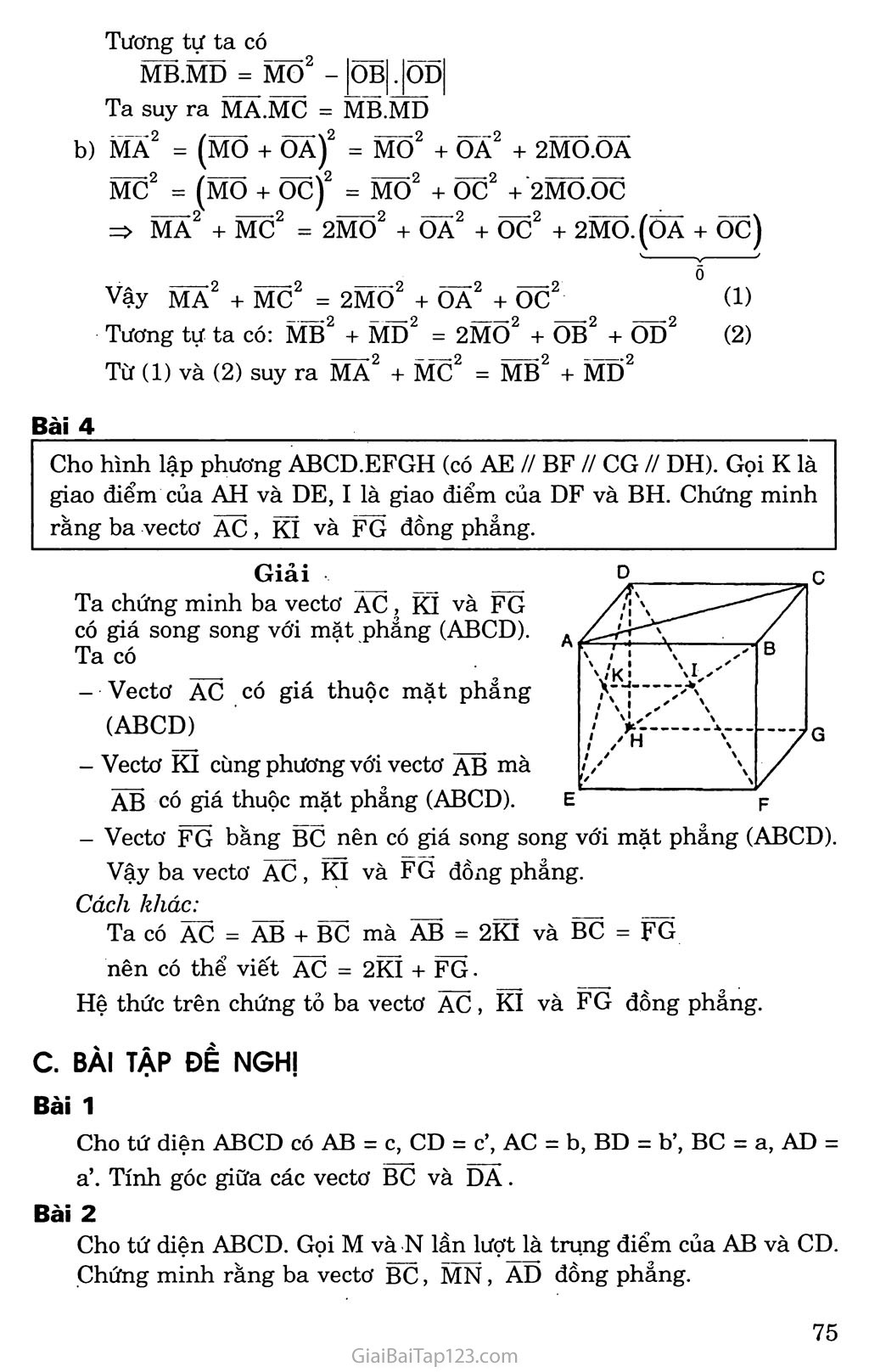
CHƯƠNG in VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN Cỉ)ắn đề 1. VECTƠ TRONG KHÔNG GIAN A. KIẾN THỨC CẦN NHỚ Các kiến thức: Định nghĩa vectơ, các phép toán về vecto' trong không gian giống như trong mặt phẳng. Sau đây sẽ hệ thống lại các kiến thức về sự đồng phẳng của 3 vectơ. Sự ĐỒNG PHẲNG Của ba VECTƠ. Định nghĩa Trong không gian, ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng. Tính chất Cho ba vecto' ã, b, C trong không gian và từ một điểm o bất kì ta vẽ Õà = ẵ, ÕB = b, ÕC = Z . Khi đó: • Ba vectơ a, b, C đồng phẳng bốn điểm o, A, B, c cùng nằm trên một mặt phẳng. • Nếu một trong ba vectơ a, b, C là vectó õ thì ba vecto' ã, b, C đồng phẳng. Điều kiện để ba vectơ đồng phẳng Định lí: Cho hai vectơ không cùng phương ã và b và một vectơ C trong không gian. Khi đó ba vectơ a, b, c đồng phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho C = ma + nb B. GIẢI BÀI TẬP SÁCH GIÁO KHOA Bài 1 Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Mặt phẳng (P) cắt các cạnh bên AA, BB’, cơ, DD’ lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ: cùng phương với IA ; cùng hướng với IA ; ngược hướng với IA ; Giải Các vectơ cùng phương với IA là: ĨAKB, KB*', LC, LC', MD, MD’ Các vectơ cùng hướng với IA là: KB, LC, MD. Các vectơ ngược hướng với IA là: IAKBLCMD' - Bài 2 Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: a) ĂB + Ẽpc*' + DD’ = Ãc*'; b) BD - DĨ) - B'D' = BB*'; Ãc + BÃ*' + DB + ci) = 5 Giải ÃB + BÌ? + DD*' = ÃB + BC + cc*' = AC*' BD - ẼTẼ) - B7]?' = BD + DẼT' + DĨ? = BB*' AC + BA*' + DB + <?D = AC + CD*' + ẼPẼ*' + ẼTẨ = ÃẨ = Õ Bài 3 Cho hình bình hành ABCD. Gọi s là một điểm nằm ngoài mặt phẳng hình bình hành. Chứng minh rằng: SA + SC = SB + SD Giải • => SA + SC = SB + SD SB + SD = 2SO Gọi o là tâm của hình bình hành ABCD. Khi đó: SA + SC = 2SO Bài 4 Cho hình tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng: MN = |(ÃD + BC); b) MN = Ỉ(ÃC + BD) 2 2 Giải a) MN = MA + AD + DN MN = MB + BC + CN => 2MN = ÃD + BC => MN '= ị(ÃD + BC) 2 MN = MA + ÃC + CN* MN = MB + BD + DN => 2MN = AC + BD => MN = |(AC + BD). Bài 5 Cho hình tứ diện ABCD. Hãy xác định hai điếm E. F sao cho: a)ÃE = ÃB + ÃC + ÃD; b)ÃF = ÃB + ÃC-ÃD. Giải a) Ta có AE = AB + AC + AD mà (AB + AC) + AD = AG + AD Với G là đỉnh thứ tư của hình bình hành ẠBGC vì AG = AB + AC. Vậy AE = AG + AD với E là đỉnh thứ tư của hình bình hành AGED Do đó AE là đường chéo của hình hộp có ba cạnh là AB, AC, AD b) Ta có AF = AB + AC - AD mà_(AB j^AC) - AD = AG - AD = DG Vậy AF = DG nên F là đỉnh thứ tư của hình bình hành ADGF. Bài 6 Giải Ta có DA = DG + GA DB = DG + GB DC = DG + GC DA + DB + DC = 3DG vì GA + GB + GC = ỗ Bài 7 Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABCD. Chứng minh rằng: Dà + DB + DC = 3DG. Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN vằ P là một điểm bất kì trong không gian. Chứng minh rằng: ' a)ĨẨ + ĨB + ĨC + ĨD = Õ; b) PI = ị(PẨ + PB + PC + PD). Giải Ta có IM + IN = õ mà 2ĨM_= IA + ĩc và 2ĨN = IB + ĨD nên 2(IM + IN) = õ hay Là + ĨB + ĩc + ĨD = õ Với điểm p bất kì trong không gian ta có: M/ / X / X / ' 1 ĨẨ = PA - PI, ĨB = PB - PỈ ĩc = PC -PI, ĨD = PD -PỈ. Vậy IA + IB + IC + ID = PẤ + PB + PC + PD - 4PI mà theo câu a), ta có IA + IB + IC + ID = õ nên suy ra: PĨ = ị (Pà + PB + PC + PD). 4 Bài 8 ■ Cho hình lăng trụ tam giác ABC.A’B’C’ có AA ’ = ã, AB = b, AC = C. Hãy phân tích (hay biểu thị) các vectơ B’C, BC' qua các vectơ a, b, c Giải B' c = AC - AB1 = AC - (AA' + AB) = c — a — b BC*' = ÁC' - ÃB = (ÃÃ*' + ÃC) - AB = a + c - b Bài 9 Cho tam giác ABC. Lấy điễm s nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho MS = -2MA và trên đoạn BC lấy điểm N sao cho NB = “NC. Chứng minh rằng ba vectơ AB, MN, sc đồng phẳng. Giải MN = MS + sc + CN (1) MN = MA + ÃB + BN => 2MN = 2MA + 2ÃB + 2BN (2) Cộng (1) với (2) ta được: 3MN = MS + 2MẠ + sc + 2ÃB + CN + 2BN 0 0 Vậy MN = ịsC + ^ÃB 3 3 Do đó ba vectơ MN, sc, AB đồng phảng. Bài 10 Cho hình hộp ABCD.EFGH. Gọi K là giao điểm cũa AH và DE, I là giao điểm của BH và DF. Chứng minh ba vectơ AC, KI, FG đồng phang. Giải Ta có KI // EF // AB nên KI // mp(ABC), FG // BC và AC c mp(ABC) Do đó ba vecto- KI, FG, AC có giá cùng song song vói một mặt phẳng (a ) là mặt phẳng song song với mặt phẳng (ABC). Vậy ba vectơ KI, FG, AC đồng phảng. c. BÀI TẬP BỔ SUNG Bài 1 Cho hình hộp ABCD.A’B’C’D’ (có AA’ // BB’// CC’ // DD’). Chứng minh rằng, a) ÃB + ÃD + AA~' = AC' b) BD - D' D - B'D' = BB1. Giải AB + AD + ÃÃ’ = ÃB + BC + CC' = ẦC' BD - D ’ D - BrD' = BD + DẼT + D'B' = BB' Bài 2 Cho bốn điểm A, B, c và D không đồng phẳng. Trên đoạn thẳng AD lấy điểm M, sao cho MẨ = -2MD và trên đoạn thẳng BC lấy điểm N, sao cho NB = -2NC. Chứng minh rằng ba vectơÀB , DC và MN đồng phẳng. Giải (1) (2) Theo giả thiết ta cổ Mà = -2MD và NB - -2NC Ta có MN = M + AB + BN và MN = MD + DC + CN (2) => 2 MN - 2MD + 2DC + 2CN (3) _ c Ta cộng đẳng thức (1) và (3) với nhau vế theo vế, có 3MN = AB + 2DC vì Mà + 2MD = 0,BN + 2CN = õ hay MN = |ãB + |õc. Vậy ba vectơ MN, AB và DC đồng phảng.' Bài 3 Cho hình chữ nhật ABCD và một điểm M tùy ý. Chứng minh rằng: MA.MC = MB.MD Giải Gọi o là tâm hình chữ nhật. Ta có ' |oa| = |oổ| = |õc|'= Ịõd|. a) MA.MC = (mõ + ÕĂ).(MÕ + oc) MA2 + MC2 = MB2 + MD2. = MÓ + OA.ÕC + MO.(oà + oe) = MO + OA.OC MA.MC = MÕ2-|ÕÃ|. lõcl Tương tự ta có OB ,|OD Ta suy ra MA.MC = MB.MD b) MA2 = (mo + ÕÃ)2 = MÕ2 + ÕÃ2 + 2MÕ.ÕẤ MB.MD = M02 - MC (MO + OC) = MO +OC +2MO.OC MA2 + MC2 = 2MO2 + ÕÃ2 + ÕC2 + 2MÕ.(Õà + Õc) V. > (1) (2) Vậy MA2 + MC2 = 2MO2 + ÕA2 + oc2 Tương tự ta có: MB2 + MD2 = 2MO2 + OB2 + OD2 Từ (1) và (2) suy ra MA2 + MC2 = MB2 + ML)2 Bài 4 Cho hình lập phương ABCD.EFGH (có AE // BF // CG // DH). Gọi K là giao điểm của AH và DE, I là giao điểm của DF và BH. Chứng minh rằng ba vectơ AC , KI và FG đồng phẳng. Giải Ta chứng minh ba vectơ Ãc , KI và FG có giá song song với mặt phảng (ABCD). Ta có Vectơ AC có giá thuộc mặt phảng . (ABCD) Vectơ KI cùng phương với vectơ AB mà ÃB có giá thuộc mặt phẳng (ABCD). Vectơ FG bằng BC nên có giá song song với mặt phẳng (ABCD). Vậy ba vectơ Àc , KI và FG đồng phẳng. Cách kliác: Ta có AC = AB + BC mà AB = 2KI và BC = FG nên có thể viết AC - 2KI + FG- Hệ thức trên chứng tỏ ba vectơ AC, KI và FG đồng phẳng. c. BÀI TẬP ĐỀ NGHỊ Bài 1 Cho tứ diện ABCD có AB = c, CD = c’, AC = b, BD = b’, BC = a, AD = a’. Tính góc giữa các vectơ BC và DA. Bài 2 Cho tứ diện ABCD. Gọi M và N lần lượt là trụng điểm của AB và CD. Chứng minh rằng ba vectơ BC, MN, ÃD đồng phẳng. Bài 3 Cho tứ diện ABCD; M và N lần lượt là trung điểm của AB và CD. Lấy các điểm p, Q lần lượt thuộc các đường thẳng AD và BC sao cho PA = kPD, QB = kQC (k 1). Chứng miĩih rằng các điểm M, N, p, Q cùng thuộc một mặt phẳng. Bài 4 Cho hình hộp ABCD.A’B’C’D’ vói tâm o và AB = a, AD = b, AA’ - c. Chứng minh rằng với mọi điểm M ta có £= MA2 + MB2 + MC2 + MD2 + MA'2+ MB'2+ MC'2+ MD'2. = 8MO2 + 2(a2 + b2 + c2)- Hãy xác định vị trí của điếm M đế X nhận giá trị bé nhất. Bài 5 Chứng minh rằng các trung điểm của các cạnh AB, BB’, B’C’, C’D’, D’D, DA của hình hộp ABCD.A’B’C’D’ cùng nằm trên một mặt phẳng. Bài 6 ' z Cho hình lăng trụ tam giác ABC.A’B’C’, Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau. Bài 7 Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của Cũ và DD’; G và G’ lần lượt là trọng tâm các tứ diện A’D’M’N và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phảng (ABBA.’) song song với nhau. Bài 8 Trong không gian cho tam giác ABC. Chứng minh rằng nếu điểm M thuộc mp(ABC) thì OM = xÕẨ + yÕB + zOC, với mọi điểm o, trong đó X + y + z = 1. Ngược lại nếu có một điểm o trong không gian sao cho ÕM = xOA + yOB + zÕC, trong đóx + y + z = l thì điểm M thuộc mp (ABC). Bài 9 Cho tứ diện ABCD. Gọi Ax, Bx, cx, Dx là các điểm lần lượt thuộc đường thẳng AB, BC, CD, DA sao cho AXA = kÃxB, BjB = kBjC , CjC = kCxD , DXD - kDxA . Với giá trị nào của k thì bốn điểm Ax, Bj, cx, Dx cùng thuộc một mặt phảng?