SGK Đại Số và Giải Tích 11 - Bài 1. Hàm lượng giác

Bản quyền thuộc Nhà xuất bản Giáo dục Việt Nam - Bộ Giáo dục và Đào tạo.
Rfim sú Lượns Gltìc vft PRƯ0T1G TRÌITH LượnG Gltìc
sú LUỤĨÌG GlOC VẾ PtìirOTÌG TRÌÍIR LƯỌTIG Giflc
Tiếp tục phần giá trị lượng giác và các công thức lượng giác được học trong chương cuối của Đại số 10, chương này cung cấp kiến thức về hàm số lượng giác và cách giải phưong trinh lượng giác. ở đây chỉ yêu cầu giải thành thạo các phương trình cơ bản và những phương trình bậc nhất và bậc hai đối với một hàm số lượng giác.
Khác với những hàm số đã được học trước đây, các hàm sốy=sinx,y=cosX, J=tanx vày=cotxlà những hàm sô' tuần hoàn. Các hàm sô' này gặp nhiều trong các môn khoa học ứng dụng (Vật lí, Hoá học,...)
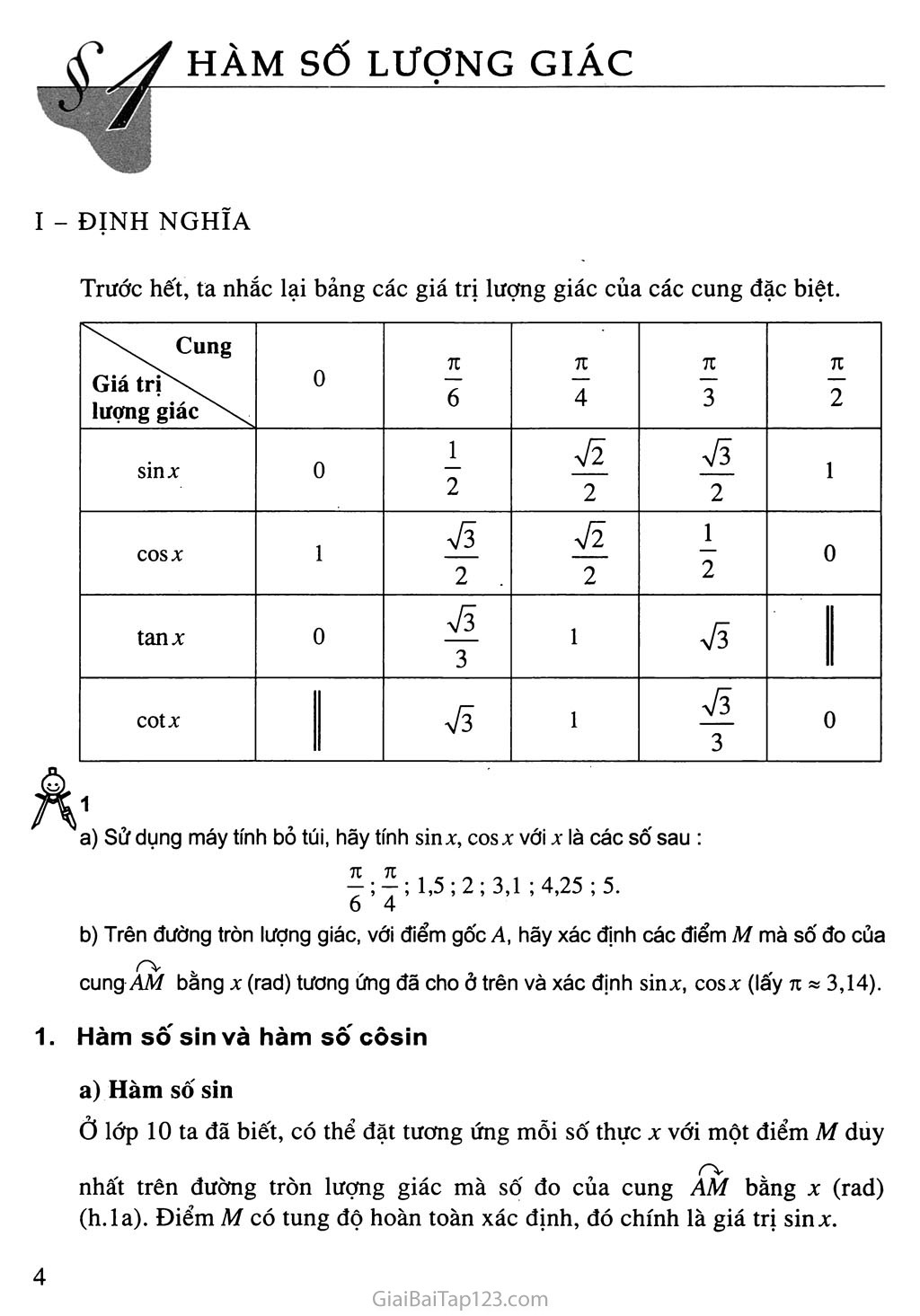
I - ĐỊNH NGHĨA
n 7Ĩ 6 ; 4
; 1,5 ; 2 ; 3,1 ; 4,25 ; 5.
HÀM SỐ LƯỢNG GIÁC
	 	•	
b) Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bang X (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lay 71 » 3,14).
Hàm số sin và hàm số côsin
Hàm sô sin
Ở lớp 10 ta đã biết, có thể đặt tương ứng mỗi số thực X với một điểm M duy
nhất trên đường tròn lượng giác mà số đo của cung AM bang X (rad) (h.la). Điểm M có tung độ hoàn toàn xác định, đó chính là giá trị sinx.
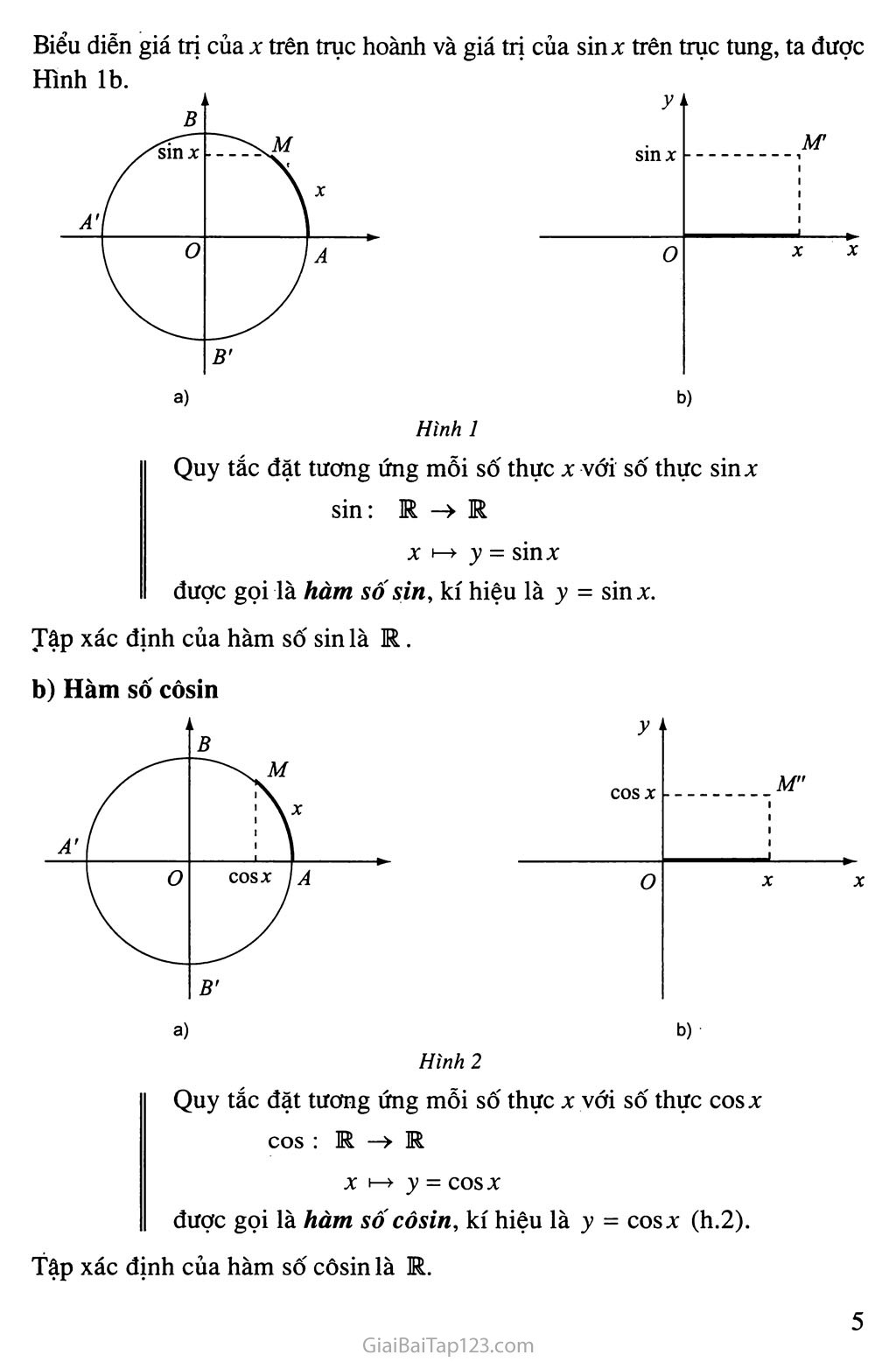
Biểu diễn giá trị của X trên trục hoành và giá trị của sinx trên trục tung, ta được
sinx
M'
1
1
1
1
1
0
X	X
b)
Hình 1
Quy tắc đặt tương ứng mỗi số thực X với số thực sinx sin: R —> R
X i—> y = sinx
được gọi là hàm sô' sin, kí hiệu là y = sin %.
Tập xác định của hàm số sin là R.
Hình 2
Quy tắc đặt tương ứng mỗi số thực X với số thực COS X cos : R —> R
X H-> y = cos X
được gọi là hàm sô' côsin, kí hiệu là y = cosx (h.2). Tập xác định của hàm số côsin là R.
Hàm số tang và hàm số côtang
Hàm sô tang
Hàm số tang là hàm số được xác định bởi công thức
sinx	.	 ,
y =	(cosx 0),
cosx
kí hiệu là y = tanx.
Vì cos X * 0 khi và chỉ khi X *	+ kit (k e Z) nên tập xác định của hàm
số y = tanx là
D = K \	+ kn, k e z\.
Hàm số côtang
Hàm số côtang là hàm số được xác định bởí công thức cosx ,
smx
y = ——— (sinx 0),
kí hiệu là y - cot X.
Vì sinx 0 khi và chỉ khi X * kiĩ (k e Z) nên tập xác định của hàm số y = cotx là
D = R \ {kít, & e z }.
so sánh các giá trị sinx và sin (-x), cosx và cos(-x).
NHẬN XÉT
Hàm số y - sin X là hàm số lẻ, hàm số y = COS X là hàm số chẵn, từ đó suy ra các hàm sô' y = tan X và y - cot X đều là những hàm số lẻ.
II - TÍNH TUẦN HOÀN CỦA HÀM số LƯỢNG GIÁC
3
Tìm những sô' T sao cho/Ị.r + T) =fix) với mọi X thuộc tập xác định của các hàm sô' sau : a)/(x) = sinx;	b)/(x) = tanx.
Người ta chứng minh được rằng T = 271 là số dương nhỏ nhất thoả mãn đẳng thức
sin(x + T) = sin %, Vr 6 I (xem Bài đọc thêm).
Hàm số y = sin X thoả mãn đẳng thức trên được gọi là hàm sô' tuần hoàn với chu kì 271.
Tương tự, hàm số y = cosx là hàm số tuần hoàn với chu kì 271.
Các hàm số y = tanx và y = cotx cũng là những hàm số tuần hoàn, với chu kì 71.
III - Sự BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM số LƯỢNG GIÁC
Hàmsốj = sinx
Từ định nghĩa ta thấy hàm số y = sin % :
Xác định với mọi xe R và -1 < sinx < 1 ;
Là hàm số lẻ ;
• Là hàm số tuần hoàn với chu kì 271.
Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.
Sự biến thiên và đồ thị hàm sô y = sinx trên đoạn [0 ; 7t]
71^
Xétcác số thực Xị, x2, trong đó 0<X! <x2<	■ Đặt x3 = 7Ĩ - x2, x4 = 71 - Xp
Biểu diễn chúng trên đường tròn lượng giác và xét sinx,- tương ứng (ỉ = 1, 2, 3,4)
Khi đó x3, x4 thuộc đoạn
và x3 sinx4.
7T
Vậy hàm số y = sin.Y đồng biến trên
và nghịch biến trên
71
Bảng biến thiên :
X
0
71
2
71
y = sin.Y
0
^^0
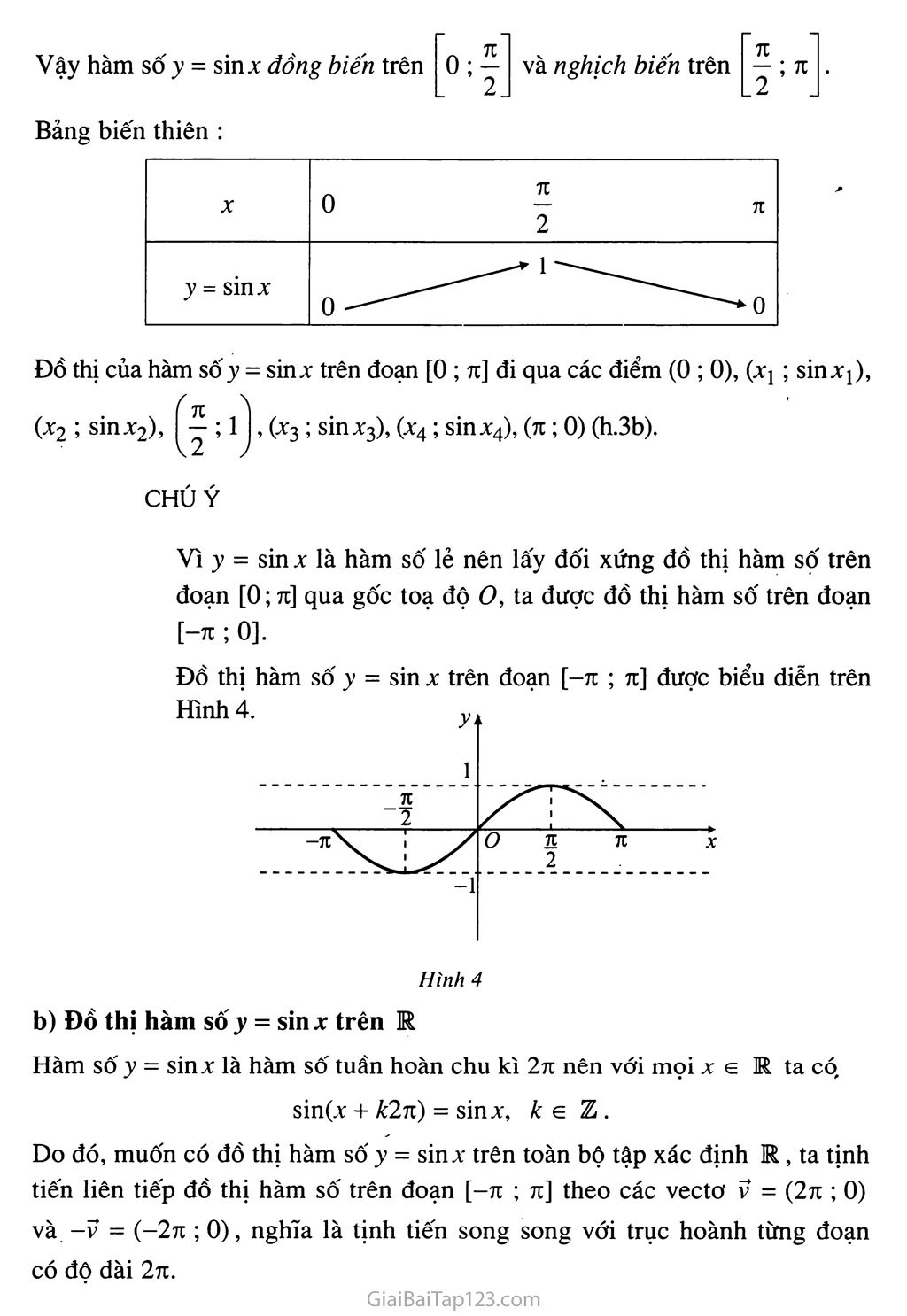
ĐỒ thị của hàm sốy = sinx trên đoạn [0 ; 71] đi qua các điểm (0 ; 0), (%Ị; sin a:ị), (%2 ; sinx2),	, (%3; sinx3), (x4; sinx4), (7t; 0) (h.3b).
CHÚ Ý
Đồ thị hàm số y = sin X trên đoạn [—TC ; 7ĩ] được biểu diễn trên
Vì y - sin X là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn [0; 7i] qua gốc toạ độ o, ta được đồ thị hàm số trên đoạn [-k;0].
Hình 4
Đồ thị hàm sô y = sin X trên R
Hàm số y = sinx là hàm số tuần hoàn chu kì 271 nên với mọi X e R ta có sin(x + k2ri) - sin %, k e z .
Do đó, muốn có đồ thị hàm số y = sin.v trên toàn bộ tập xác định R, ta tịnh tiến liên tiếp đồ thị hàm số trên đoạn [-71 ; 7ĩ] theo các vectơ V = (2tĩ ; 0) và -V = (-271 ; 0), nghĩa là tịnh tiến song song với trục hoành từng đoạn có độ dài 27Ĩ.
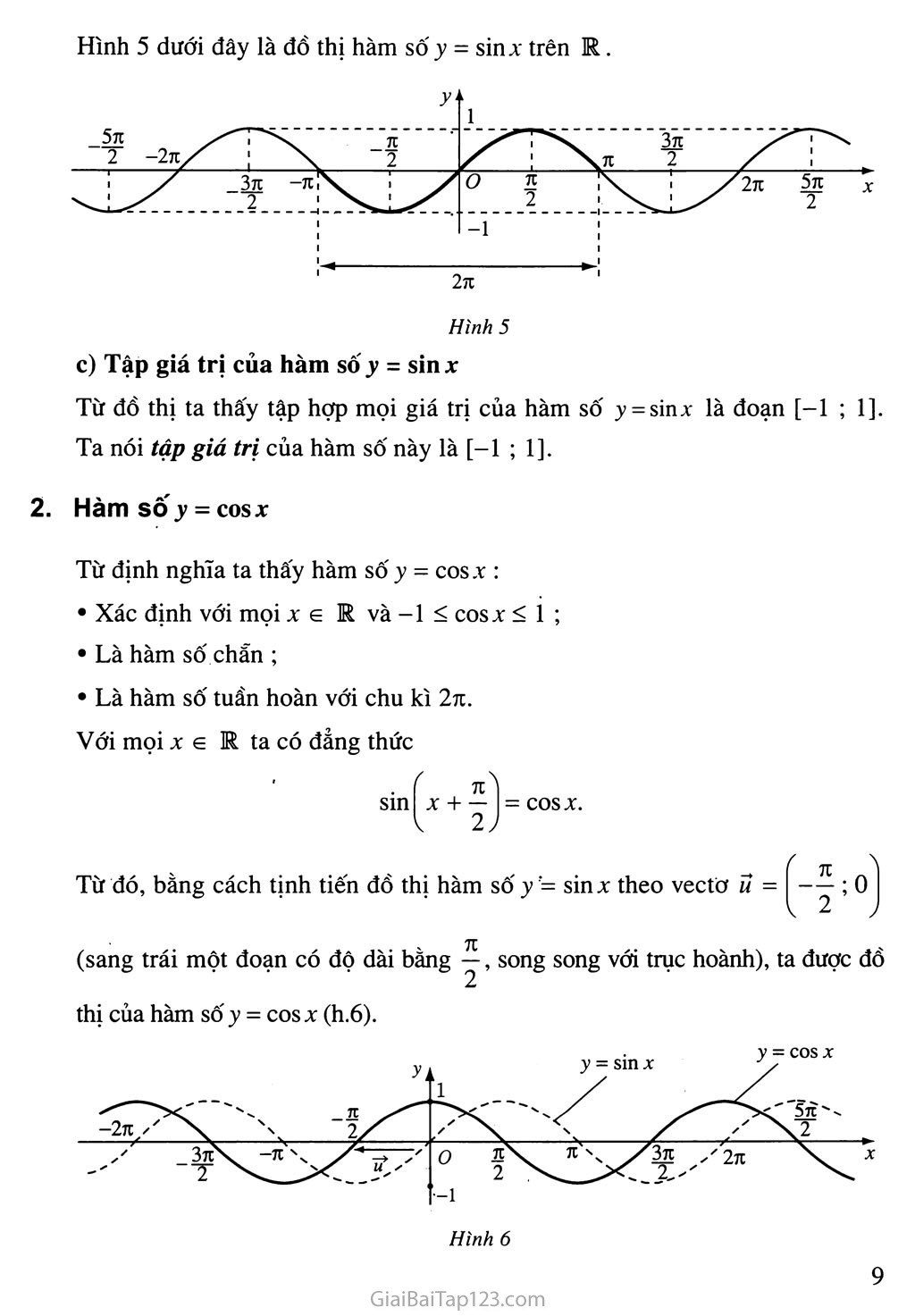
Hình 5 dưới đây là đồ thị hàm số y = sin X trên R.
Tập giá trị của hàm sôy = sinx
Từ đồ thị ta thấy tập hợp mọi giá trị của hàm số y = sinx là đoạn [-1 ; 1]. Ta nói tập giá trị của hàm số này là [-1 ; 1],
Hàm số y = cosx
Từ định nghĩa ta thấy hàm số y = cosx :
Xác định với mọi X e R và -1 < cosx < 1 ;
Là hàm số chẩn ;
Là hàm số tuần hoàn với chu kì 2tc.
Với mọi xe R ta có đẳng thức
sin
Từ đó, bằng cách tịnh tiến đồ thị hàm số y - sinx theo vectơ ĩỉ =
71
;0
(sang trái một đoạn có độ dài bằng , song song với trục hoành), ta được đồ
cosx.
Từ đồ thị của hàm số y = cosx trên Hình 6, ta suy ra :
Hàm sốy = cosx đồng biến trên đoạn [-71; 0] và nghịch biến trên đoạn [0 ; 7i]. Bảng biến thiên :
X
-n
0
71
y = COS %
-1
1
"^-1
Tập giá trị của hàm số y = cos.v là [-1 ; 1],
Đồ thị của các hàm số y = COS À, y = sinx được gọi chung là các đường hình sin.
Hàm sô y = tanx
Từ định nghĩa ta thấy hàm số y = tan.v :
Có tập xác định là£> = R \ +'kn,k e z ị- ;
Là hàm số lẻ ;
Là hàm số tuần hoàn với chu kì 7t.
Vì vậy, để xét sự biến thiên và vẽ đồ thị của hàm số y = tan X, ta chỉ cần xét sự
V -'7	 .	r	71 >
71 7Ĩ
biến thiên và vẽ đồ thị của hàm số này trên nửa khoảng 0 ; 2 I ’ sau đó lấy đối
xứng qua gốc toạ độ 0, ta được đồ thị hàm số trên khoảng --7 ; _ ■ • 1 2 2
Sự biến thiên và đồ thị hàm sôy = tanx trên nửa khoảng 0 ; y Ị
,7	-	7	_	71
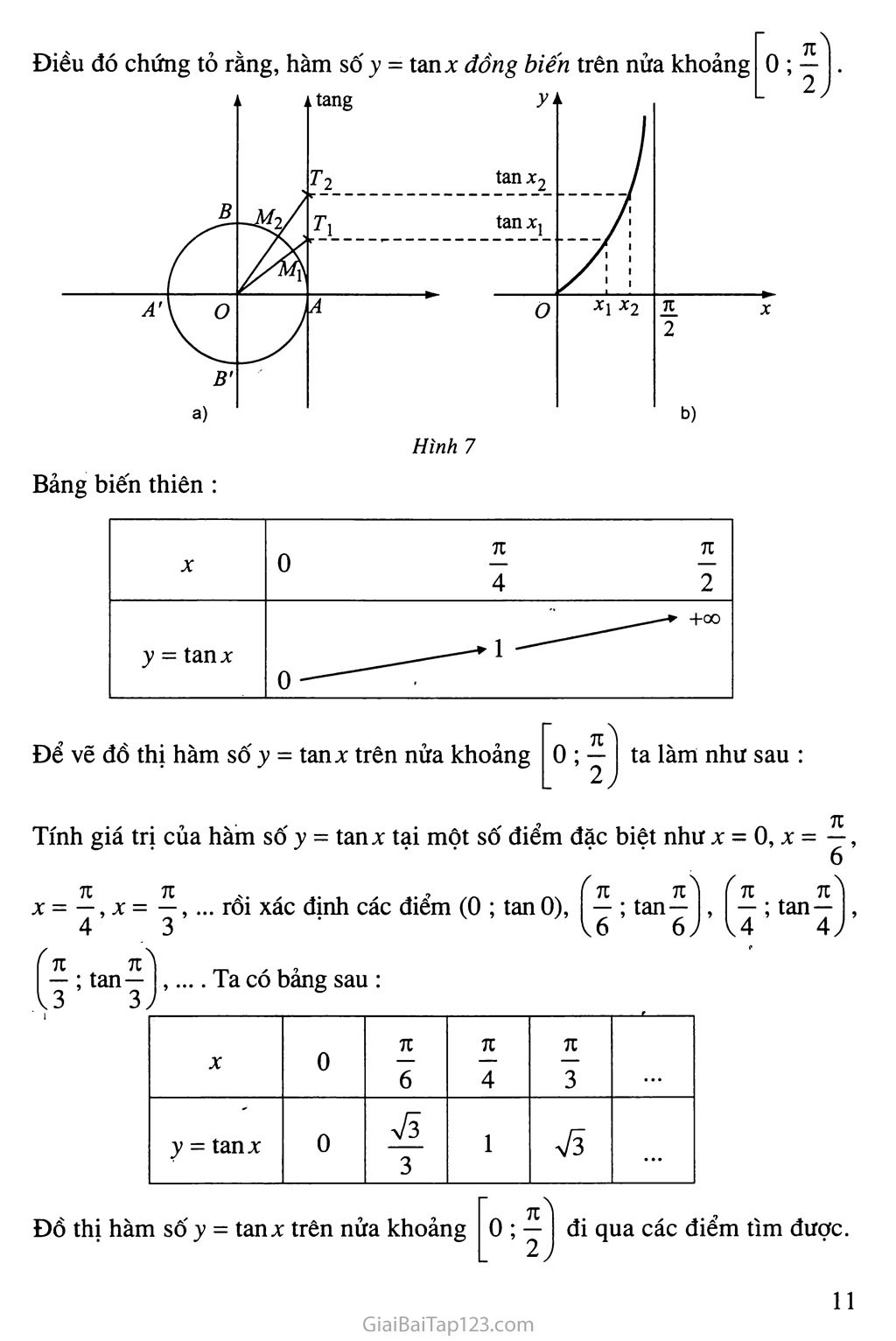
Từ biếu diên hình học của tanx (h.7a), với Xị, x2 e 0 ; Ỷ I, AMị = Xỵ,
rv	"777	“777
AM2 = x2, AT 1 = tan.Yj, AT2 = tanx2, ta thấy :
Xị tan.Yj < tan.v2.
X
0
71
4
71
2
	>1 -
	* +CO
y = tanx
0	'
Để vẽ đồ thị hàm số y - tanx trên nửa khoảng
ta làm như sau :
71
Tính giá trị của hàm số y = tanx tại một số điểm đặc biệt như X = 0, X =
6
;tany^j ’ — • Ta có bảng sau :
X
0
71
6
71
4
7ĩ
ĩ
y - tanx
0
3
1
Vã
...
,	,	71^	x 9 v
ĐỒ thị hàm số y - tanx trên nửa khoảng 0 ; I đi qua các điếm tìm được.
Nhận xét rằng khi X càng gần Ỷ thì đồ thị hàm số y - tan X càng gần đường thẳng X- y (h.7b).
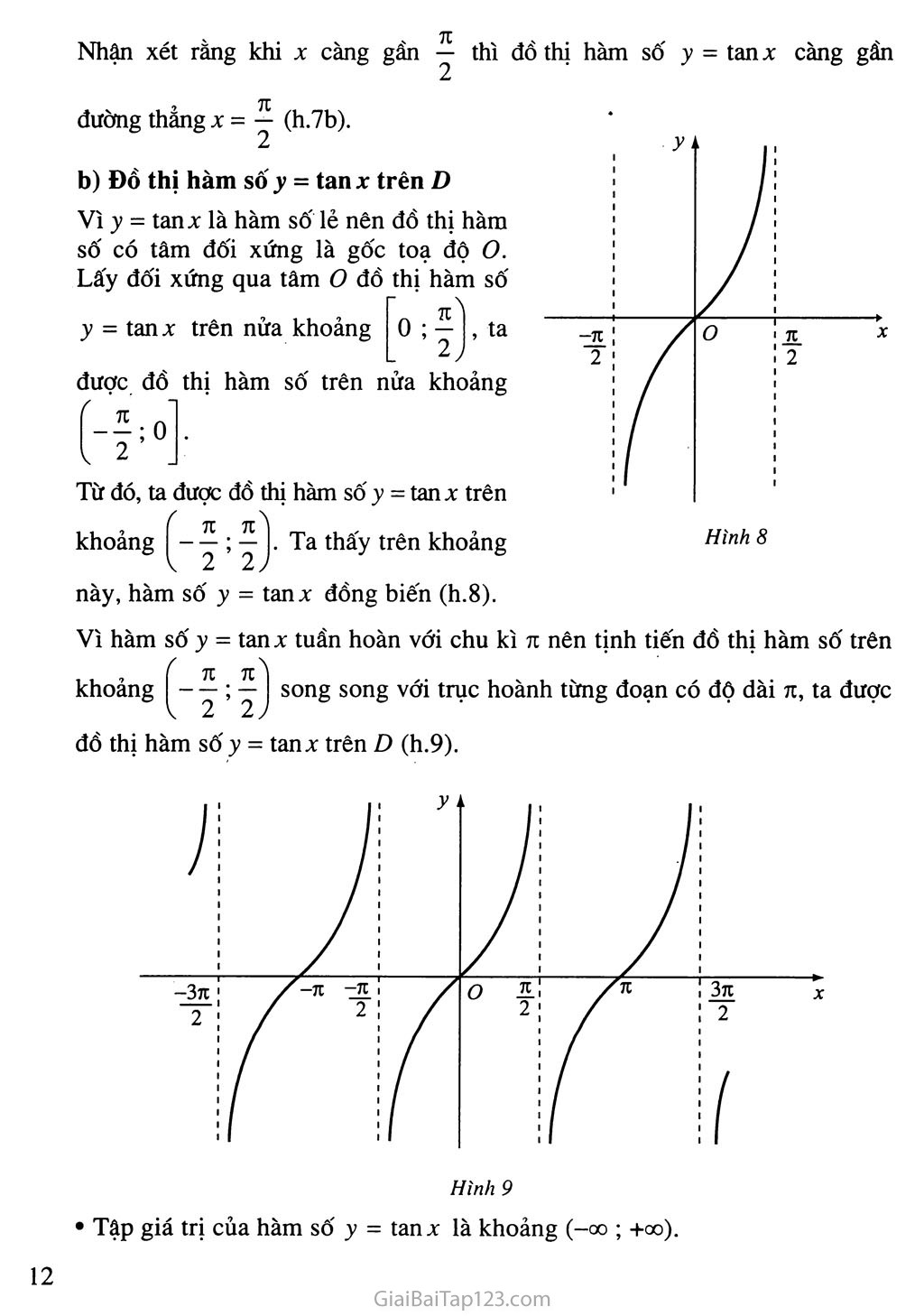
Đồ thị hàm sô y = tan X trên D
Vì y = tanx là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc toạ độ o. Lấy đối xứng qua tâm o đồ thị hàm số
/	, r/
y = tan X trên nửa khoảng 0 ; Ỷ I, ta được đồ thị hàm số trên nửa khoảng
-f;0
Từ đó, ta được đồ thị hàm số y = tan X trên khoảng	Ta thấy trên khoảng này, hàm số y = tanx đồng biến (h.8).
Vì hàm số y - tan X tuần hoàn với chu kì 71 nên tịnh tiến đồ thị hàm số trên 9 I 71 7C I
khoảng I - 2 ’ 2 J s°ng s°ng vớt trục hoành đoạn có độ dài 71, ta được đồ thị hàm số y - tanx trên D (h.9).
Hàmsốy = cotx
Từ định nghĩa ta thấy hàm số y = cotx :
Có tập xác định là D - R \ {kn, k e z } ;
Là hàm số lẻ ;
Là hàm số tuần hoàn với chu kì lĩ.
Sau đây, ta xét sự biến thiên và đồ thị của hàm số y = cotx trên khoảng (0; 7t), rồi từ đó suy ra đồ thị của hàm số trên D.
Sự biến thiên và đồ thị hàm sô y = cotx trên khoảng (0 ; 7ĩ)
Với hai số Xị và x2 sao cho 0 < Xị < x2 < 71, ta có 0 < x2 - Xị < 7C. Do đó
cos Xi cos Xọ
cot Xi - cot x2 = —— 	;——
sin Xj sin x2
_ sin x2 cos Xj - cos x2 sin Xỵ
sin Xị sin x2
= sin(x2 - X|) > 0 sin Xj sin x2
hay cotXj > cotx2.
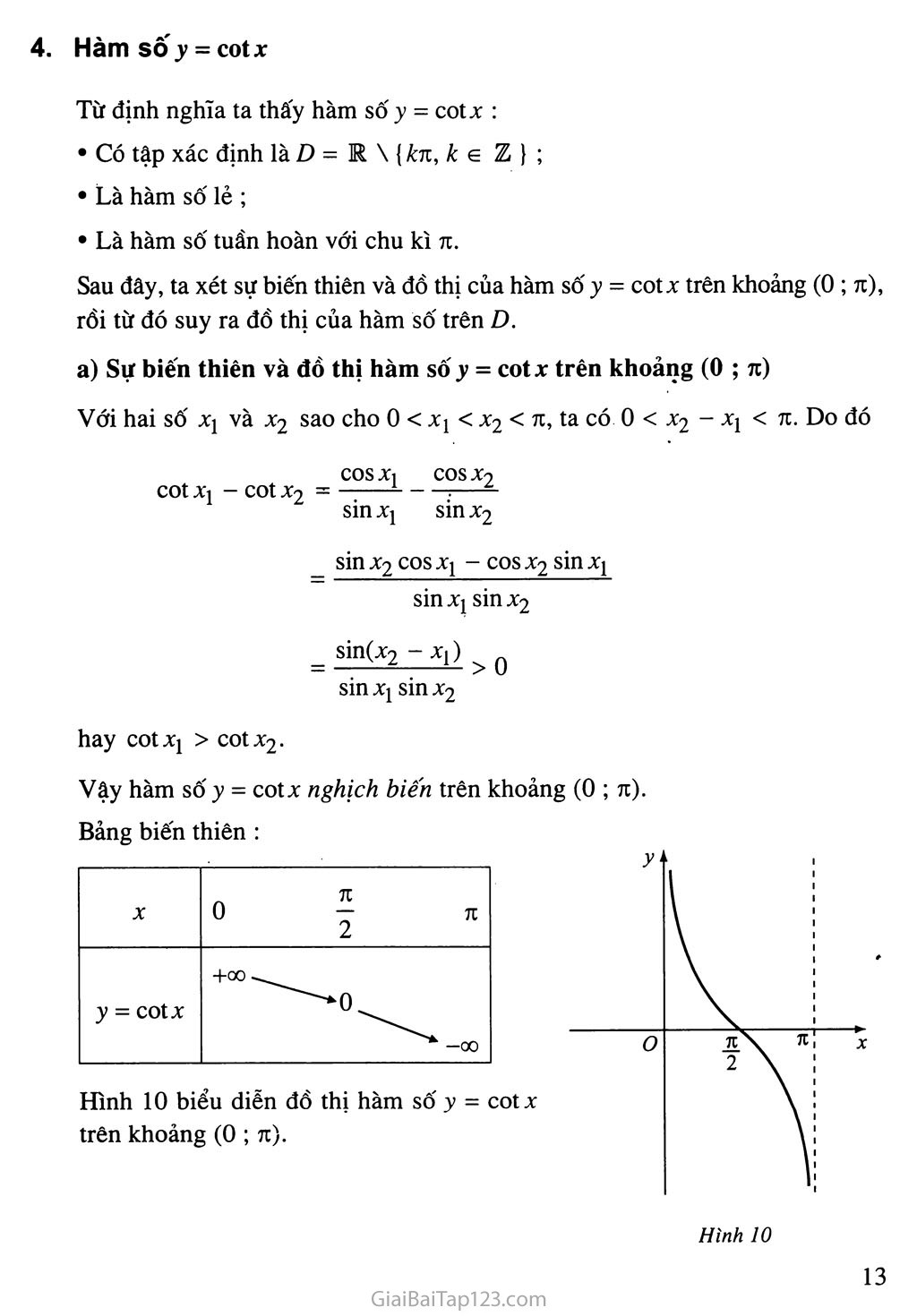
Vậy hàm số y = cotx nghịch biến trên khoảng (0 ; 7i). Bảng biến thiên :
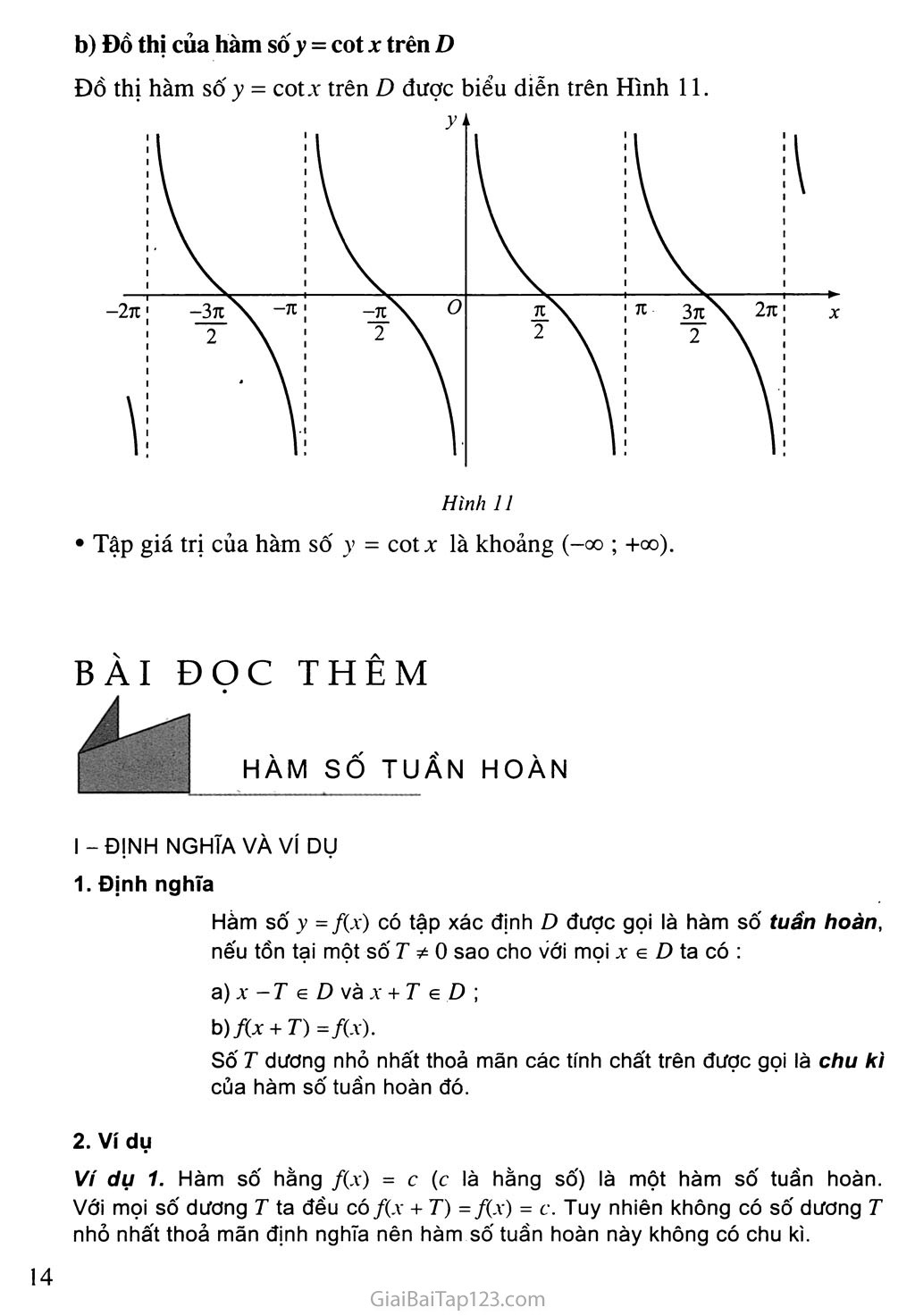
Đồ thị của hàm SÔJ' = cot X trên I)
Hình 11
• Tập giá trị của hàm số y = cotx là khoảng (-00 ; +oo).
BÀI ĐOC THÊM
HÀM SỐ TUẦN HOÀN
I - ĐỊNH NGHĨA VÀ ví DỤ
Định nghĩa
Hầm số y = /(%) có tập xác định D được gọi là hàm số tuần hoàn, nếu tồn tại một SỐT *0 sao cho với mọi X e D ta có :
X - T e D và X + T e D ;
/(x + n =/(*).
Sô T dương nhỏ nhất thoả mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
Ví dụ
Ví dụ 1. Hàm số hằng /(x) = c (c là hằng số) là một hàm số tuần hoàn. Với mọi số dương T ta đều cóf(x + T) =/(a) = c. Tuy nhiên không có số dương T nhỏ nhất thoả mãn định nghĩa nên hàm số tuần hoàn này không có chu kì.
Ví dụ 2. Hàm phần nguyên y = [%] đã được nêu trong Đại sô' 10.
Ta xét hàm y = {X} xác định bởi : {%} = x- [%]. Nó được gọi là hàm phần lẻ của X. Chẳng hạn, {4,3} = 4,3 - 4 = 0,3 ;
{-4,3} =-4,3 -(-5) = 0,7.
Ta chứng tỏ hàm y = {%} là hàm tuần hoàn với chu kì là 1.
Thật vậy, {x + 1} = X + 1 - [% + 1] = X + 1 - [x] - 1 = X - [x] = {x }.
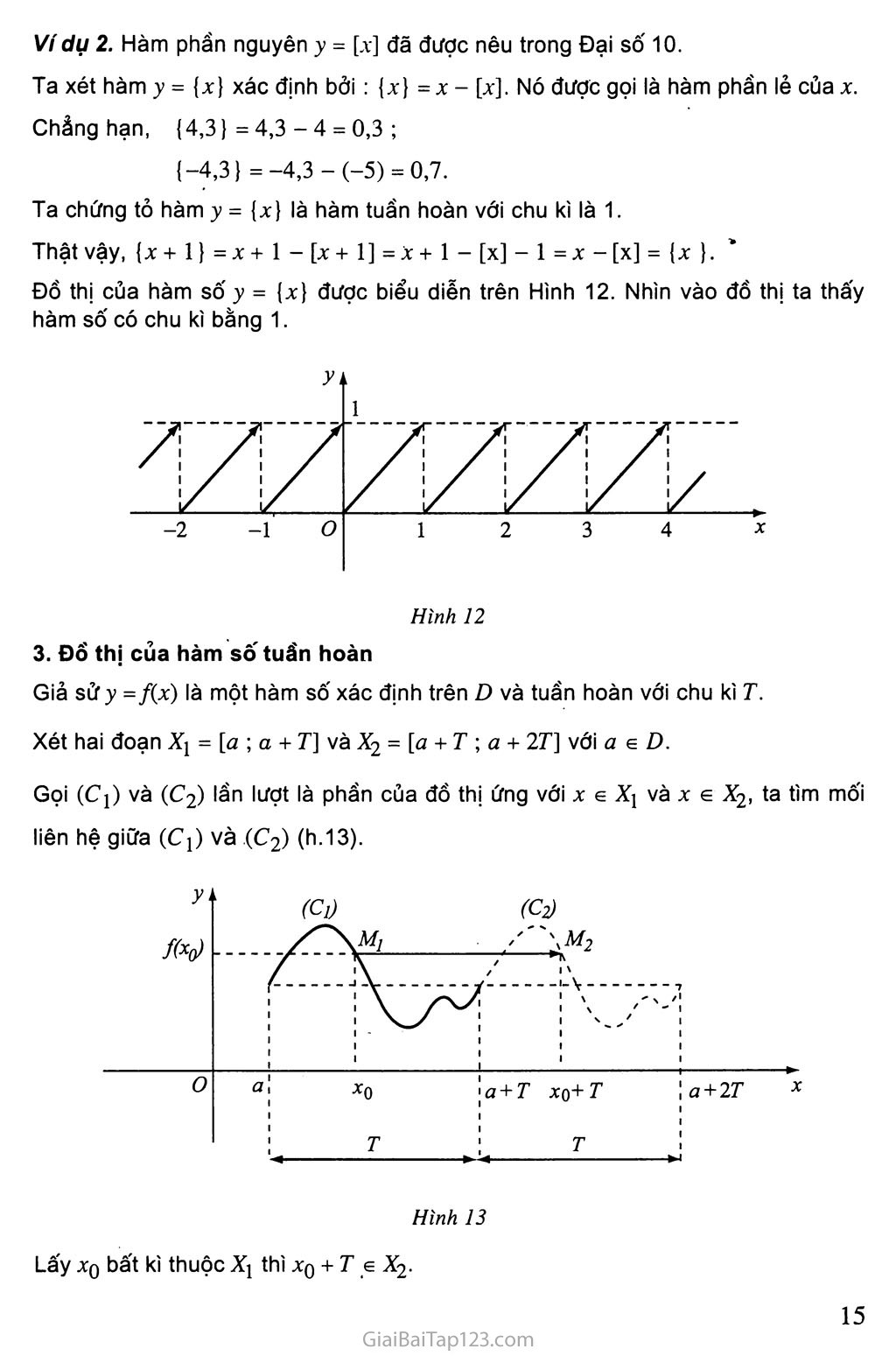
Đồ thị của hàm số y = {%} được biểu diễn trên Hình 12. Nhìn vào đồ thị ta thấy hàm số có chu kì bằng 1.
Đồ thị của hàm số tuần hoàn
Giả sử)’ =/(x) là một hàm sô' xác định trên D và tuần hoàn với chu kì T.
Xét hai đoạn %! = [a ; a + rj và x2 = ta + T ; a + 2T] với a e D.
Gọi (Cị) và (C2) lần lượt là phần của đồ thị ứng với X e Xỵ và X e x2, ta tìm mối liên hệ giữa (Cj) và (C2) (h.13).
Hình 13
Lấy XQ bất kì thuộc Xị thì A'o + T e x2.
Xét hai điểm Mị và Mọ lần lượt thuộc (Cị) và (C2), trong đó
Ta có	= (x2 - XỊ ; T2 ~ Ti) = (^ ; 0) = V (V không đổi).
Suy ra M2 là ảnh của Mỵ trong phép tịnh tiến theo vectơ V. Vậy "(C2) là ảnh của (Cj) trong phép tịnh tiến theo vectơ V".
Từ đó, muốn vẽ đồ thị của hàm sô' tuần hoàn chu kì T, ta chỉ cần vẽ đồ thị của hàm số này trên đoạn [a ; a + T], sau đó thực hiện lần lượt các phép tịnh tiến theo các vectơ V, 2v, và các vectơ -V, -2v, ... ta được toàn bộ đồ thị của hàm số.
II - TÍNH TUẦN HOÀN CỦA HÀM số LƯỢNG GIÁC
Tính tuần hoàn và chu kì của các hàm sốy = sinx và J = cosx
ĐỊNH LÍ 1
Các hàm số V = sinx và y = cosx là những hàm sô' tuần hoàn với chu kì 2ĩi. -
Chứng minh. Ta chứng minh cho hàm số y = sinx (trường hợp hàm sô' y = cosx được chứng minh tương tự).
Hàm sô' y = sinx có tập xác định là R và với mọi sô' thực X ta có
(1)
(2)
X - 2tĩ e R. .v+ 2n e R ,
sin(x + 2tc) = sinx.
Vậy y = sinx là hàm sô' tuần hoàn. Ta chứng minh 2rc là sô' dương nhỏ nhất thoả mãn các tính chất (1) và (2).
Giả sử có sô' T sao cho 0 < T < 2ji và siii(x + T) = sinx, Vx e R .
Chọn X = 77, ta được
sin	= sin— = 1 cosT = 1.
Điều này trái giả thiết 0 < T < 2tc.
Vậy 2te là sô' dương nhỏ nhất thoả mãn tính chất (2), nghĩa là 2rc là chu kì của hàm sô'y = sinx. ■
Tính tuần hoàn và chu kì của các hàm sốy = tanx vày = cotx
ĐỊNH LÍ 2
f	’	ì
Các hàm số y = tanx và y = cotx là những hàm số tuần hoàn với chu kì 71.	z
Chứng minh. Ta chứng minh cho hàm sô' y = tanx, (trường hợp hàm sô' y = cotx được chứng minh tương tự).
Hàm sô' y = tanx có tập xác định D = R \	k e
Với mọi í e D ta CÓI-1I e ữ và í + n e ũ, tan(x + Tt) = tanx.
Vậyy = tanxlà hàm sô' tuần hoàn. Ta chứng minh 71 là chu kì của hàm sô' này.
Giả sử có sô' T sao cho 0 < T < 71 và tan(x + T) = tanx, Vx e D.
Chọn X = 0 thì X e D và tan(0 + T) = tan 0 = 0.
Nhưng tan a = 0 khi và chỉ khi a - kn, k G z , do đó phải có T = kĩĩ, k e z. Điều này mâu thuẫn với giả thiết 0 < T < 71.
Vậy chu kì của hàm sô' y = tanx là 71. ■
Bài tạp
1. Hãy xác định các giá trị của X trên đoạn
a) Nhận giá trị bằng 0 ; c) Nhận giá trị dương ;
Tìm tập xác định của các hàm số : 1 + COS X
a)y =
sinx
c)y= tan^x - y) ;
3 71
.^2.
để hàm số y = tanx :
b) Nhận giá trị bằng 1 ; d) Nhận giá .trị âm.
b) y =
Í1 + COS X 1 - cosx
	f tcA
d) y = cotl X + — I.
3.
4.
Dựa vào đồ thị của hàm số y = sinx, hãy vẽ đồ thị của hàm số y = Isinxl.
Chứng minh rằng sin 2(x + kỉì) - sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin 2x.
Dựa vào đồ thị hàm số y = cosx, tìm các giá trị của X để cosx =
Dựa vào đồ thị hàm số y - sinx, tìm các khoảng giá trị của X để hàm số đó nhận giá trị dương.
Dựa vào đồ thị hàm số y = cosx, tìm các khoảng giá trị của X để hàm số đó nhận giá trị âm.
Tìm giá trị lớn nhất của các hàm số :
y = 2-ựcosx + 1 ;
y - 3 - 2 sin X.