SGK Đại Số và Giải Tích 11 - Bài 2. Dãy số

- ĐỊNH NGHĨA
1
Cho hàm so/(n) = -!-, M G N*. Tính/(1) ,/(2),/(3),/(4) J(5).
2«-l
Định nghĩa dãy SỐ
Mỗi hàm số u xác định trên tập các số nguyên dương N* được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu :
M : N* -» R n H-> m(m).
Người ta thường viết dãy số dưới dạng khai triển m2’ w3’ •••’ U)V •••■>
trong đó un = u(ỉi) hoặc viết tắt là (m„), và gọi «1 là sô' hạng đầu, un là số , hạng thứ n và là số hạng tổng quát của dãy số.
Vídụl
Dãy các số tự nhiên lẻ 1, 3, 5, 7, ... có số hạng đầu Uỵ = 1, số hạng tổng quát un = 2« - 1.
Dãy các số chính phương 1, 4, 9, 16, ... có số hạng đầu Mị = 1, số hạng tống quát un = n .
Định nghĩa dãy số hữu hạn
Mỗi hàm số u xác định trên tập M = {1, 2, 3,..., m} với m e N* được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là Mị, M2, w3’ •••’ unv trong đó Mị là số hạng đầu, um là sô'hạng cuối.
Ví dụ 2
-5, -2, 1, 4, 7, 10, 13 là dãy số hữu hạn có Uị = -5, «7 = 13.
là dãy số hữu hạn có Mị = -,«5=
- CÁCH CHO MỘT DÃY số
& L.	„h4„ „ „A. 44m	„4 du mi„H H„4
/ "Hãy nêu các phương pháp cho một hàm sô và ví dụ minh hoạ.
Dãy số cho bằng công thức của số hạng tổng quát
Ví dụ 3
(1)
b) Dãy số (m„) với un
y/Tì + 1 1	2	3
có dạng khai triển là
2’ 72 +1’ 73 +1’ ’’’’77 +1’ ’”
Như vậy, dãy số («„) hoàn toàn xác định nếu biết công thức số hạng tổng quát un của nó.
i Viết năm số hạng đầu và số hạng tổng quát của các dãy số sau :
Dãy nghịch đảo của các số tự nhiên lẻ ;
Dãy các số tự nhiên chia cho 3 dư 1.
Cũng giống như hàm số, không phải mọi dãy số đều có công thức số hạng tổng quát M„. Dưới đây, ta nêu thêm các cách khác để cho một dãy số.
Dãy sô cho bằng phương pháp mô tả
Ví dụ 4. Số 71 là số thập phân vô hạn không tuần hoàn 7Ĩ = 3,141 592 653 589...
Nếu lập dãy số («„) với un là giá trị gần đúng thiếu của số 7Ĩ với sai số tuyệt đối 10"" thì
Hj = 3,1 ; «2 = 3,14 ; «3 = 3,141 ; «4 = 3,1415 ; ... .
Đó là dãy số được cho bằng phương pháp mô tả, trong đó chỉ ra cách viết các số hạng liên tiếp của dãy.
Dãy SỐ cho bằng phương pháp truy hồi
Ví dụ 5. Dãy Phi-bô-na-xi' Phi-bô-na-xi (Fibonacci, 1170 - 1250) - Thương gia, nhà toán học I-ta-li-a.
’ là dãy số (w„) được xác định như sau :
*
Mị = ^2 = 1
un - un_ỵ + w„_2 với n > 3,
nghĩa là, kể từ số hạng thứ ba trở đi, mỗi số hạng đều bằng tổng của hai số hạng đứng ngay trước nó.
Cách cho dãy số như trên được gọi là cho bằng phương pháp truy hồi.
Nói cách khác, cho một dãy số bằng phương pháp truy hồi, tức là :
Cho số hạng đầu (hay vài số hạng đầu).
Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.
4
Viết mười sô' hạng đầu của dãy Phi-bô-na-xi.
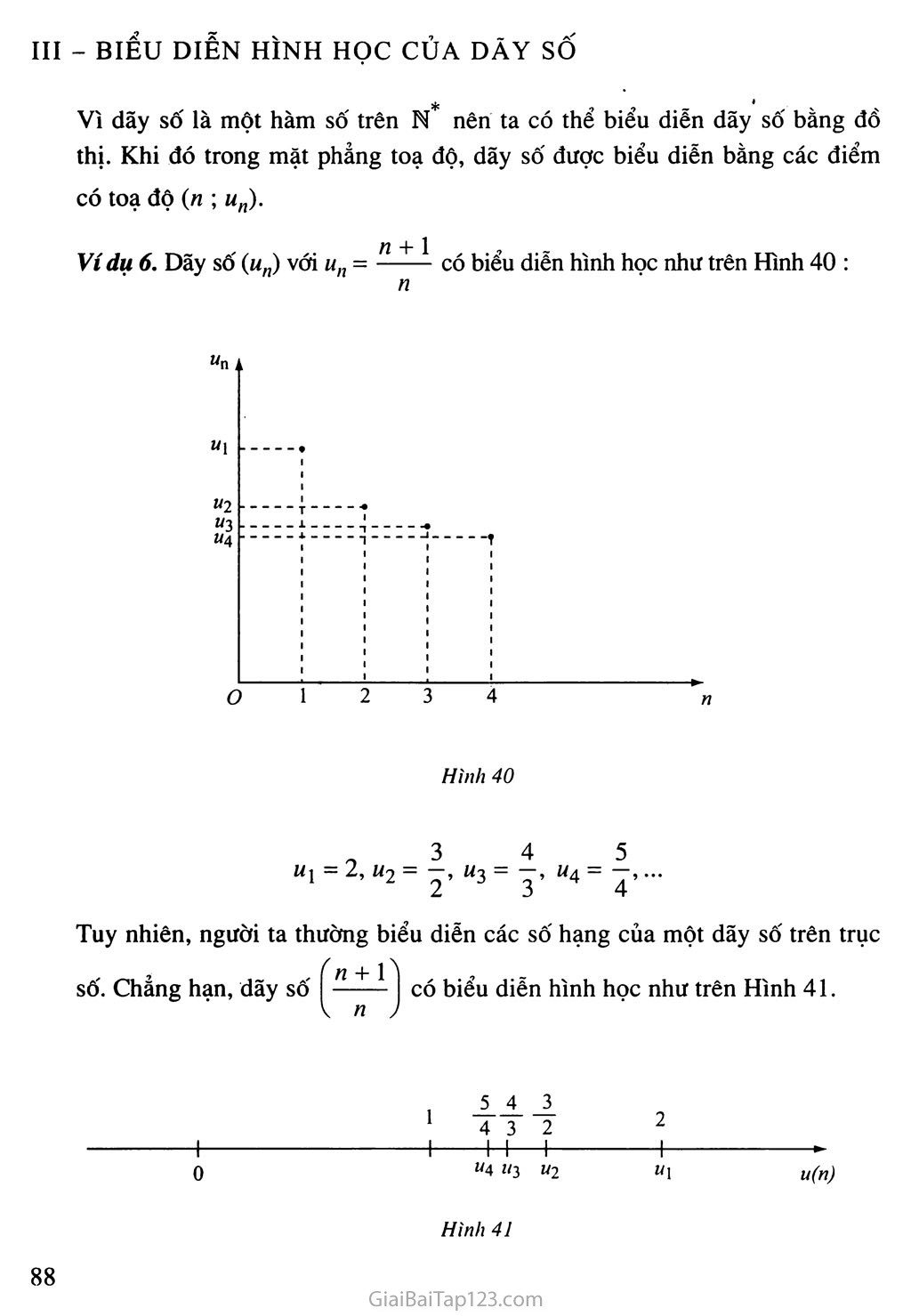
Ill	- BIỂU DIỄN HÌNH HỌC CỦA DÃY số
Vì dãy số là một hàm số trên N nên ta có thể biểu diễn dãy số bằng đồ thị. Khi đó trong mặt phẳng toạ độ, dãy số được biểu diễn bằng các điểm có toạ độ (« ; M„).
/7 + 1	,	in 1 4A
Ví dụ 6. Dãy số («„) với = —— có biếu diên hình học như trên Hình 40 : n
»1
«2
«3
»4
ơ 1	2	3	4
Hình 40
«1=2» «2= P «3 = ỹ
Tuy nhiên, người ta thường biểu diễn các số hạng của một dãy số trên trục số. Chẳng hạn, dãy số + có biểu diễn hình học như trên Hình 41.
5 4	3
4 3 2	2
II	ĩ	1	-
M4 «3	»2	“1	u(n)
Hình 41
- DÃY SỐ TẢNG, DÃY số GIẢM VÀ DÃY số BỊ CHẶN
^Lcăcdâvsó,„,và(v.,v^..1 + i;^5„-,.
Cho các dãy số (w„) và (v„) với un = 1 + — ; v„ = 5„ - 1.
n
Tính un+ỉ, vn+ỉ.
Chứng minh «ÍJ+1 vn , với mọi n e N* .
Dãy số tăng, dãy số giảm
ĐỊNH NGHĨA 1
Dãy số (w„) được gọi là dãy sô' tăng nếu ta có un+ỵ > un với
*
mọi n e N .
Dãy số (i/„) được gọi là dãy số giảm nếu ta có M„+J < u„ với
*
mọi n e N .
Ví dụ 7. Dãy số («„) với un = 2n - 1 là dãy số tăng.
Thật vậy, với mọi n e N xét hiệu W„+Ị - un. Ta có
M«+l - un = 2(rt + 1) - 1 - (2/1 - 1) = 2. Do Ww+l - w„ > 0 nên Un+Ị > un. ■
Ví dụ 8. Dãy số («„) với
/2
-y là dãy số giảm. 3n
*	9	li 1 _L_ 1
Thật vậy, với mọi n e N , vì un > 0 nên có thể xét tỉ số ——. Ta có un
Dễ thấy
n + 1
3«
< 1 nên
Wfl + 1	n + 1 n n + 1
w„ = 3rt+1 : 3” = 3«
< 1 suy ra mzị+1 < un. ■
CHƯ Y
Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số (w„) với un = (-3)”, tức là dãy
-3,9,-27,81,... không tăng và cũng không giảm.
Dãy số bị chặn
Chứng minh các bất đẳng thức
n +1	2	2«
> 1, V/ỉ e N
ĐỊNH NGHĨA 2
Dãy số (w„) được gọi là bị chặn trên nếu tồn tại một số M sao cho
un < M,\/n e N .
Dãy số (w„) được gọi là bị.chặn dưới nếu tồn tại một số m sao cho
*
un >m,\/ne N .
Dãy số (w„) được gọi là z»ị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho
m < un < M, V/7 e N*.
Ví dụ 9
Dãy số Phi-bô-na-xi bị chặn dưới vì un > 1 với mọi ne N*.
/2	n 1
K2 + 1
Dãy số («„) với u„ =	— bị chặn vì 0 < —r-— < — ■
HOA, LÁ VÀ DÃY SỐ PHI-BÔ-NA-XI
Dãy sô' Phi-bô-na-xi thường gặp trong thiên nhiên. Những chiếc lá trên canh cây mọc cách nhau các khoảng ứng với các sô' trong dãy sô' Phi-bô-na-xi (còn gọi là các sô' Phi-bô-na-xi) 3,5,8,13,21,34,55,89,...	(F)
Sô' cánh hoa trong hầu hết các bông hoa là các sô' trong dãy (F). Hoa loa kèn có 3 cánh, hoa mao lương vàng có 5 cánh, hoa phi yến có 8 cánh, hoa cúc vạn thọ 13 cánh, hoa cúc tây 21 cánh, còn hoa cúc thường có 34 hoặc 55, hoặc 89 canh.
Fibonacci
' (1170- 1250)
Hoa hướng dương
Ngoài những điều thú vị trên, một sô' vấn đề của kiến trúc, hội hoạ, âm nhạc, ... cũng liên quan đến các sô' Phi-bổ-na-xi.
Trong hoa hướng dương cũng xuất hiện các sô' Phi-bô-na-xi. Những nụ nhỏ kết thành hạt ở đầu bông hoa và xếp thành hai lớp đường xoắn ốc. Một lớp cuộn theo chiều kim đồng họ, lớp đường xoắn kia cuộn theo chiều ngược lại. So các đường xoắn ốc theo chiều kim đồng*hồ thường là 34 hoặc 55, con sô' đường xoắn theo chiều ngược lại thường là 55 hoặc 89, ..?
Bài tập
Viết năm số hạng đầu của các dãy số có số hạng tổng quát un cho bởi công thức :
b) un =
2" -1
2n + 1
d) un =
2n - 1
un = 1 +
Cho dãy số (w„), biết:
Wj=-1, «„+! = un + 3 với n > 1.
Viết năm số hạng đầu của dãy số.
Chứng minh bằng phương pháp quy nạp : un - 3/7 - 4.
Dãy số (w„) cho bởi:
«1 = 3; u„+1 = ựl + «2 , /7 > 1.
Viết năm số hạng đầu của dãy số.
Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
Xét tính tăng, giảm của các dãy số («„), biết:
c) «„ = (-!)" (2"+l);
b) un =
d)w„ =
/7-1 n + 1 ’ 2/7 + 1 5/7 + 2
5. Trong các dãy số (m„) sau, dãy số nào bị chặn dưới, bị chặn trên và bị chặn ?
1
2 ,
a) un = 2/7 - 1 ;
1
c) = —ỹ— 2«z - 1
b) =
/7(/7 + 2)
d) un - sin n + COS n.