SGK Đại Số và Giải Tích 11 - Bài 2. Giới hạn của hàm số

- GIỚI HẠN HỮU HẠN CỦA HÀM số TẠI MỘT DIEM
Xét hàm sô' /(x):
2x2 - 2x
x-1
1. Định nghĩa
1. Cho biến X những giá trị khác 1 lập thành dãy sô' (x„), xn -> 1 như trong bảng sau :
X
Xị = 2
3
x9 = —
2 2
■'t 1 cn
II
4°
5
*4	4
n+1
X"n
	> 1
/(■*)
/Ui)
/(*2)
/(*3)
/U4)
f(*n)
	► 9
Khi đó, các giá trị tương ứng của hàm sô'
/Uj), /(x2), ...,/(xn),...
cũng lập thành một dãy sô' mà ta kí hiệu là (/(xZỊ)).
a) Chứng minh rằng /(xw) - 2xn = 2n + 2
b) Tìm giới hạn của dãy sô' (/(x„)).
2. Chứng minh rằng với dãy sô' bất kì (xn), xn*ỉ và xn -> 1, ta luôn có /(x ) -> 2.
2x2 -2x
x-1
có giới hạn là 2
(Với tính chất thể hiện trong câu 2, ta nói hàm sô' /(x) = khi X dần tới 1).
Dưới đây, thay cho các khoảng (), (-00 ; Ế»), (ữ ; +oo) hoặc (-00 ; +oo), ta viết chung là khoảng K.
ĐỊNH NGHĨA 1
Cho khoảng K chứa điểm +0 và hàm số y = /(x) xác định trên K hoặc trên K\ {x0}.
Ta nói hàm số y -fix') có giới hạn là số L khi X dần tới +0 nếu với dãy số (à'/;) bất kì, xne K\ {x0( vàx„ —> x0, ta cố jfxn) L.
Kí hiệu : lim /(%) = L hay /(x) -» L khi X —> %0.
x2 _4
Ví dụ 1. Cho hàm số /(x) = —	Chứng minh rằng lim /(x) = -4.
X + 2	x->-2
Giải. Hàm số đã cho xác định trên R \ {-2}.
Giả sử (x„) là một dãy số bất kì, thoả mãn x„ -2 và xn —> -2 khi n —» +00. Ta có
\	*2-4	(x„+2)(x„-2)
lim/Ỵx^) = lim——- = lim————y-	= lim(xn - 2) = -4.
x„ + 2	(x„ + 2)
Do đó lim /(x) = -4. ■
X—>— 2
(Lưu ý rằng, mặc dù /(x) không xác định tại X = -2, nhưng hàm số lại có giới hạn là -4 khi X —> -2).
NHẬN XÉT
lim X = Xq ; lim c = c, với c là hằng số.
2. Định lí về giới hạn hữu hạn
Ta thừa nhận định lí sau đây.
ĐỊNH LÍ 1
Giả sử lim /(x) = L và lim g(x) = M. Khi đó
X—»xn
X-Ạ.ro
lim [/(x) + g(x)] = L'+ M;
X —> A*0
lim [/(x) - g(x)] = L- M; x-^x0
lim [/(x).g(x)] = L.M ;
X—>Xq
lim	(nếu M * 0).
x->x0 g(x) M
b) Nếu /(%) > 0 và lim /(x) = L, thì *->*0
(Dấu X * X,
với
L > 0 và lim yỊf(x) = 41.
củaf(x) được xét trên khoảng đang tìm giới hạn, <))•
X2 + 1
Ví dụ 2. Cho hàm số /(%) = -—7=^. Tìm lim /(x).
27%	x-»3
Giải. Theo Định lí 1 ta có
, , lim (%2 + 1)
lim /(%) = lim	=-
x->3	X—>3 27X	lim 24 X
x—>3
2
lim X + lim l lim X. lim X + lim l „ .
lim 2. lim 77
lim 2.
/ lim X
X —> 3	X —3
x->3	1
»Jx->3
x->3	x->3 _ x->3 x->3	x->3 _ »3 ■ 3 4~ l _ 5 _
Do đó,
X2 + X - 2	(x - l)(x + 2)	.	_ -5 »
lim	—-— = lim	-	= lim (x + 2) = 3. ■
X —> I	X 1	X —1	X 1	X —> 1
Giới hạn một bên
Trong Định nghĩa 1 về giới hạn hữu hạn của hàm số khi X —> x0, ta xét dãy số (x„) bất kì, xn e Ấ\{x0} và xn -» x0. Giá trị xn có thể lớn hơn hay nhỏ hơn x0.
Nếu ta chỉ xét các dãy (x„) mà xn luôn lớn hơn x0 (hay luôn nhỏ hơn xỡ), thì ta có định nghĩa giới hạn một bên như dưới đây.
ĐỊNH NGHĨA 2
Cho hàm số y =f(x) xác định trên khoảng (x0 ; z?).
Số L được gọi ià giới hạn bên phải của hàm số y =f(x) khi X —> Xq nếu với dãy số (x„) bất kì, x0 < x„ < b và xn x0, ta
! có/(xw) —> L.
"	Kí hiệu : lim /(x) = L.
X—>XQ
Cho hàm số y=f(x) xác định trên khoảng (ứ ; x0).
ị Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi X —» XQ nếu với dãy số (xn) bất kì, a Xq, ta có/(x„) -> L.
Kí hiệu : lim /(x) = L .
X^XQ
Ta thừa nhận định lí sau đây.
ĐỊNH LÍ 2
lim /(x) = L khi và chỉ khi lim /(x) = lim /(x) = L. x^xữ	X—>Xq	X->Xo
/(*) =
Ví dụ 4. Cho hàm số
èx + 2 nếu X > 1
(1)
(2)
Tìm lim /(x), lim /(x) và lim/(x) (nếu có). x->r	X->1+	X->1
Giải. Ta có, lim /(x) = lim (x2 - 3) = l2 - 3 = -2 ;
X —> 1	X —> 1
lim /(x) = lim (5x + 2) = 5.1 + 2 = 7.
X—>1	X—>1+
Như vậy, khi X dần tới 1 hàm số y =f(x) có giới hạn bên trái là -2 và giới hạn
bên phải là 7. Theo định lí 2, lim/(x) không tồn tại vì lim /(x) lim /(x). ■ X—>1	•	X—>1“	X—>1+
Trong biểu thức (1) xác định hàm số y =/(x) ở Ví dụ 4, cần thay số 2 bằng số nào để hàm số có giới hạn khi X -> 1 ?
- GIỚI HẠN HỮU HẠN CỦA HÀM số TẠI VÔ cực 3
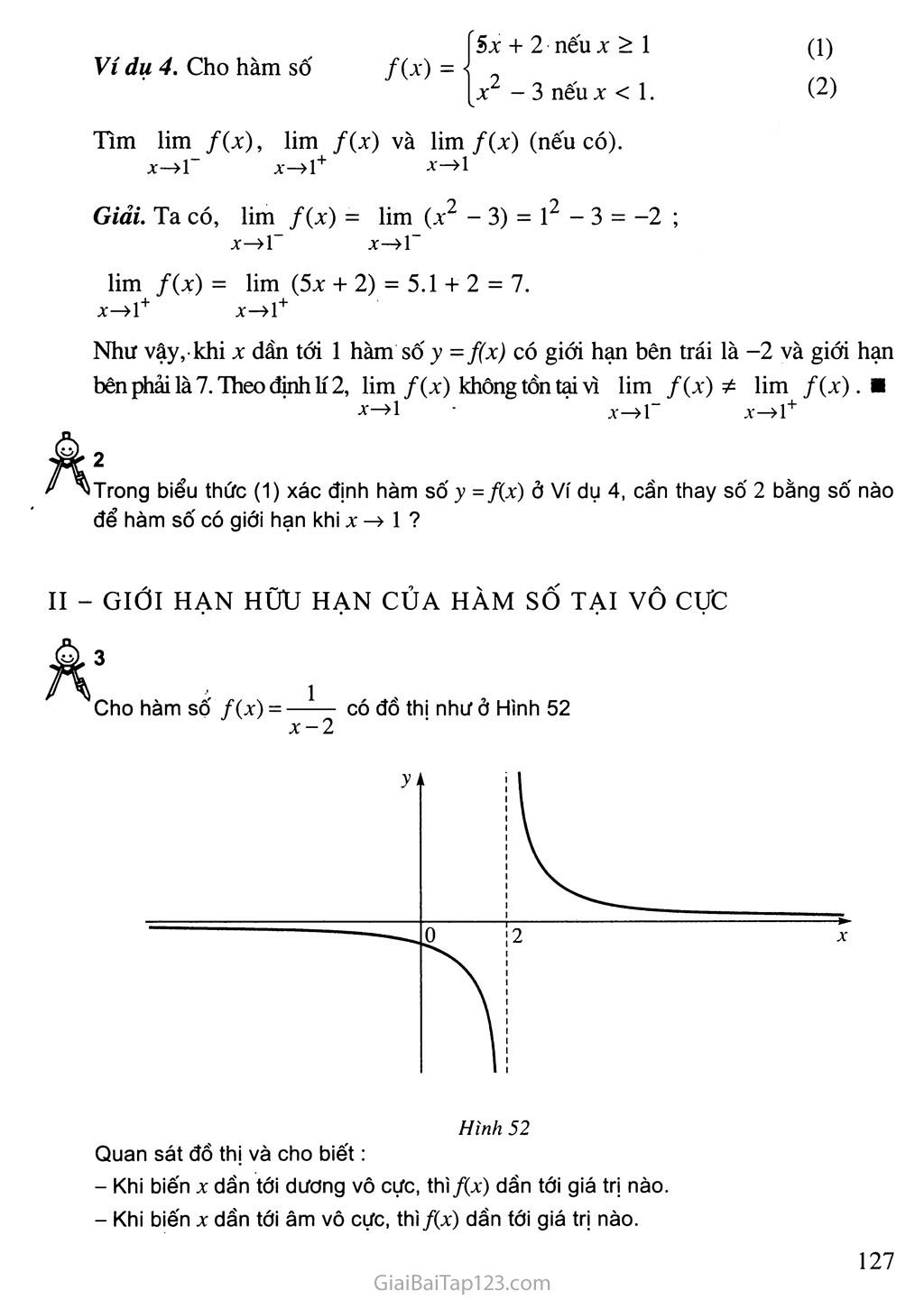
Cho hàm số /(x) - ——- có đồ thị như ỏ Hình 52 x-2
52
Quan sát đồ thị và cho biết:
Khi biến X dần tới dương vô cực, thì/(x) dần tới giá trị nào.
Khi biến X dần tới âm vô cực, thì/(x) dần tới giá trị nào.
ĐỊNH NGHĨA 3	*
Cho hàm số y =f(x) xác định trên khoảng (ứ ; +oo).
Ta nói hàm số y = f(x) có giới hạn là số L khi X —> +CO nếu với ! dãy số (x„) bất kì, xn > arì xn +00, ta có /(x„) —> L.
Kí hiệu: lim /(x) = L hay/(x) -> L khi X —> +00.
X—>+00
Cho hàm số y = /(x) xác định trên khoảng (-00 ; đ).
Ta nói hàm số y =f(x) có giới hạn là số L khi X —> -00 nếu với dãy số (x„) bất kì, xn -00, ta có /(x„) -> L.
Kí hiệu: lim /(x) = L hay/(x) —> L khi X -> -00.
X—>-00
Vỉ í/ạ 5. Cho hàm số/(x) =	Tìm lim /(x) và lim /(x).
Giải. Hàm số đã cho xác định trên (-00 ; 1) và trên (1; +oo).
Giả sử (x„) là một dãy số bất kì, thoả mãn xn -00.
Ta có lim/(xrt) = lim + 3 - lim	ỈÍL - 2.
xn - 1	1 _
Vậy lim /(x) = lim +f = 2.
X—>-00	X—>-00 X — 1
Giả sử (x„) là một dãy số bất kì, thoả mãn x„ > 1 và x„ —> +00.
+ — .
Ta có lim/(x„) = lim	—Ệ- = lim	^p~ = 2.
-1	1 _ _L
xn
Vậy lim /(x) = lim ~A + 3 =2. ■
X—>+00	X—>+00 X — 1
CHU Y
Với c, k là các hằng số và k nguyên dương, ta luôn có :
c	c
lim c = c ; lim c = c ; lim —— = 0 ; lim —— = 0.
X —>+00	X—>-00	X—>+00	X—>-00 x^
Định lí 1 về giới hạn hữu hạn của hàm số khi X —> X'o vẫn còn
đúng khi X	+CO hoặc X —> -00.
Ví dụ 6. Tìm lim 3^~2x.
X->+co X2 + 1
Giải. Chia cả tử và mẫu cho X2, ta có
Mm +4^ = 'to 3’*
X—>+00 X2 + 1
lim
X—>+00
3--
X
lim 3 - lim —
X-++00	X—>+00
X—>+00 1 	Ị_
lim
X—>+00
X2?
lim 1 + lim
X—>+oo	X—>+00 X2
3-0 1 + 0
3.
- GIỚI HẠN VÔ cực CỦẦ HÀM số
Giới hạn vô cực
Các định nghĩa về giới hạn +GO (hoặc -oo) của hàm số được phát biểu tương tự các định nghĩa 1, 2 hay 3 ở trên.
Chẳng hạn, giới hạn -00 của hàm số y = f(x) khi X dần tới dương vô cực được định nghĩa như dưới đây.
ĐỊNH NGHĨA 4
Cho hàm số y =f(x) xác định trên khoảng (ơ ; +oo).
Ta nói hàm số y = /(x) có giới hạn là -co khi X —> +00 nếu với
dãy số (x„) bất kì, xn > a và xn —> +00, ta có f(xn) -00.
Kí hiệu : lim /(x) = - 00 hay/(x) —> -00 khi X —> +00.
X—>+00
NHẬN XÉT
> id
lim /(x) = + 00 lim (-/(%)) = - 00.
X—>+00	X—>+00
Một vài giới hạn đặc biệt
lim xk = +00 với k nguyên dương.
X—>+00
lim xk ’=- 00 nếu k là số lẻ.
lim xk' = + 00 nếu k là số chẵn.
X—>-00
Một vài quy tắc về giỏi hạn vô cực
Định lí về giới hạn của tích và thương hai hàm số chỉ áp dụng được khi tất cả các hàm số được xét có giới hạn hữu hạn.
Sau đây là một vài quy tắc tính giới hạn của tích và thương hai hàm số khi một trong hai hàm số đó có giới hạn vô cực.
a) Quy tắc tìm giới hạn của tích/(x).g(x)
Nếu lim /(x) = L + 0 và lim g(x) = +00 (hoặc -oo) thì lim /(x)g(x) X—>Xq	x->x0	X—>Xq
được tính theo quy tắc cho trong bảng sau :
lim /(X)
X—>xo
lim g(x)
X-+XQ
lim /(x)g(x) x->x0
L > 0
+00
+00
—00
—00
L<0
+00
—00
—00
+00
b) Quy tác tìm giới hạn của thương —(x}
g(x)
lim /(x)
lim g(x) X—>x0
Dấu của g(x)
lim /,A') X—>Xq g(x)
L
+00
Tuỳý
0
L>0
0
V +
+00
-
—00
L<0
+
—00
-
+00
Các quy tắc trên vẫn đúng cho các trường hợp X -> XQ , X —> X'o, X —> +00 và X —> -00.
(Dấu của g(x) xét trên khoảng đang tính giới hạn, với x*x0).
Ví dụ 7. Tìm lim (xJ - 2x).
X—>-00
Í’-4Ì
= 1 > 0 nên lim X
1-
2
V	X )
X—>-00
X2 )
= — 00,
— 00 .
Giải. Ta có (x3 - 2x) = X3
3
Vì lim X = - 00 và lim
X—>-00
Vậy lim (x3 - 2x) = lim X3
X—>—00
X—>-00
Ví dụ 8. Tính các giới hạn sau :
a) lim	;
X-+1" x-ĩ
Giải
b) lim
2x - 3
X->1+ x-ỉ
a) Ta có lim (x - 1) = 0, X - 1 < 0 với mọi X < 1 và
X—1
lim (2x - 3) = 2.1 - 3 = -1 < 0.
X—>1
_	4'	2% - 3
Do do, lim ——— = +CO.
X—>1— X — 1
b) Ta có lim (x - 1) = 0, X - 1 > 0 với mọi X > 1 và
X->1
lim (2x - 3) = 2.1 - 3 =-1 < 0.
x->r
2x - 3
Do do, lim ——— = -00.
X—>1+ x — 1
Bài tập
Dùng định nghĩa, tìm các giới hạn sau :
+ 1™ x + 1 . a) lim ———
x->4 3%-2 Cho hàm số
b) lim
2-5r
*->+<» X + 3
/ơ) =
y/x + 1 nếu X > 0 2x nếu X < 0
và các dãy số («„) với M„ = —, (v„) với vn -
n	n
Tính lim un, lim vn, lim f(ụn) và lim/(v„).
Từ đó có kết luận gì về giới hạn của hàm số đã cho khi X ■
Tính các giới hạn sau :
X2 — 1
4 - X2
a) lim	;
b) lim 	—— ;
V
c) lim —-
X—>—3 X + 1
X—>-2 X + 2
X—>6
2x — 6
17
d) lim =i—- ;
e) lim	;
f) lim —
X—>+00 4 — X
-V->+co xz + 1
X—>+00
Tìm các giới hạn sau :
3x-5
2x - 7
a) lim	. ;
b) lim	;
c) lim
*->2 (x - 2)2
x->r *-l
X->1’
-2xz + X - 1
3 + X
2x-l
X + 2
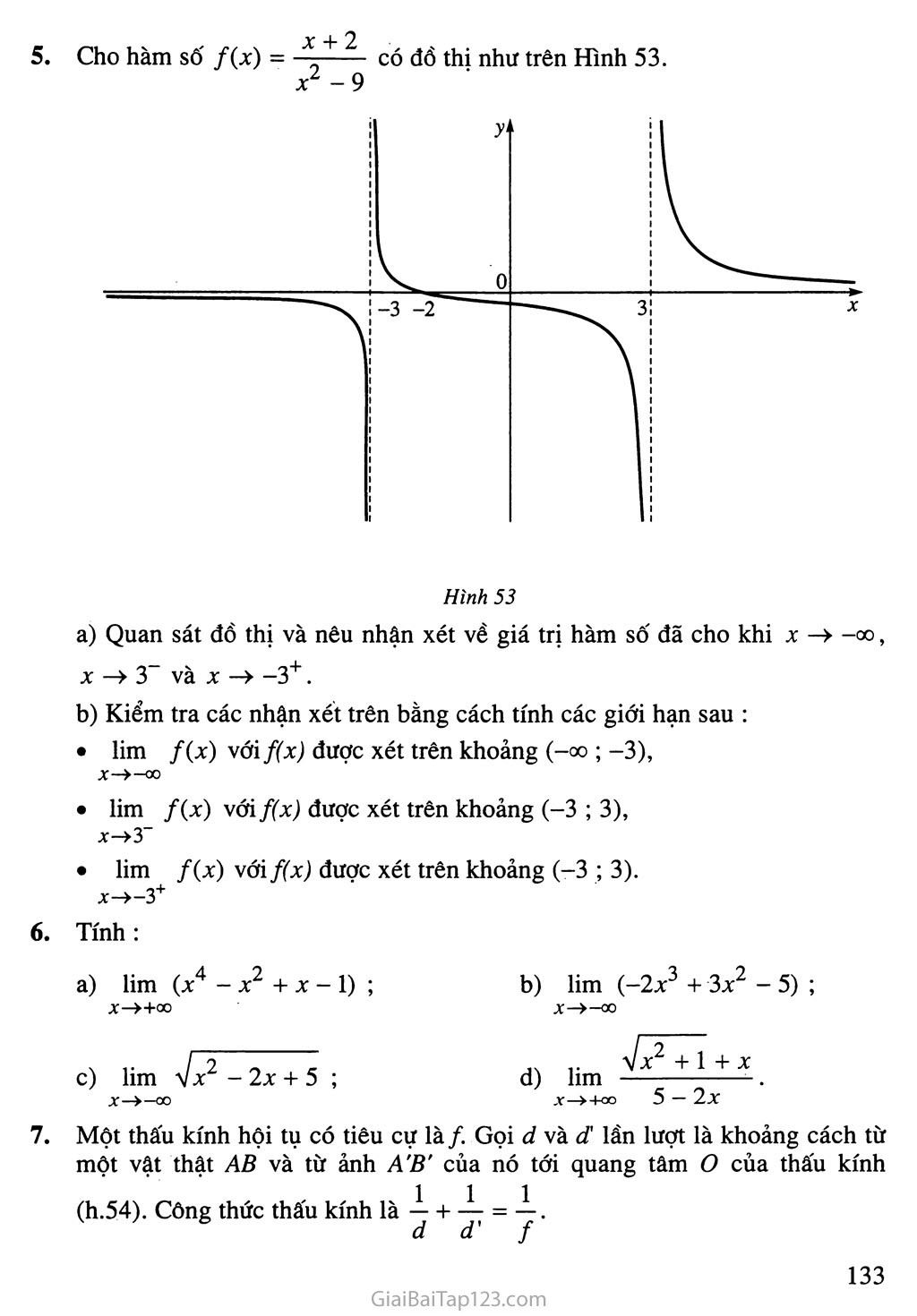
có đồ thị như trên Hình 53.
Hình 53
Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi X —> -00, X —> 3" và X —» -3+.
Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau :
• lim /(x) vớif(x) được xét trên khoảng (-«>; -3),
X—>-00
lim /(%) với f(x) được xét trên khoảng (-3 ; 3), x->3“
lim f(x) vớ[f(x) được xét trên khoảng (-3 ; 3). x->-3+
6. Tính :
a) lim (%4 - X2 + X - 1) ;
X—>+00
lim Vx2 - 2x + 5 ;
X—>-00
b) lim (-2x3+ 3x2 - 5) ;
X—>—00
i:„	+ ĩ + ■?
lim ———	.
X—>+oo	5 — 2x‘
Một thấu kính hội tụ có tiêu cự là/. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B' của nó tới quang tâm o của thấu kính
(h.54). Công thức thấu kính là 1 + ị = 1.
d d' f
►l
d	!	d'
-	 -
Hình 54
Tim biểu thức xác định hàm số d' = (p(d).
Tìm lim p(dỵ lim (p(d) và lim ạ>(dỵ Giải thích ý nghĩa của các
d->f+ d^r	4->+cc
kết quả tìm được.
BẠN CÓ BIẾT ?
1
Nhà bác học Anh Niu-tơn (Newton, 1642 - 1727) là người đầu tiên đề xuất thuật ngữ "giới hạn", dịch từ chữ La-tinh "Limes" có nghĩa là "bờ", "mép" hay "biên giới". Tuy nhiên, chính Giu-rin (Jurin, 1684 - 1750), sau đó Rô-bin (Robins, 1697 - 1751), Cô-si (Cauchy, 1789 - 1857) ... mới đưa ra các định nghĩa về khái niệm này.
Nhà toán học Đức Vai-ơ-xtrát (Weierstrass) đã trình bày một định nghĩa hiện đại về khái niệm giới hạn, gần giống với định nghĩa sau đây mà ngày nay vẫn thường được dùng trong toán học.
"Số b được gọi là giới hạn của hàm số y =f(x) khi X -> a, nếu với mỗi £ > 0, tồn tại 8 > 0 sao cho với X * a và |x - a\< s thì bất đẳng thức l/l.r) — b\ < £ được thực hiện." (Từ điển toán học NXB KH&KT 1993).
Kí hiệu "lim" mà ta dùng ngày nay là do nhà toán học Thuỵ Sĩ Luy-lơ (L’Huiller, 1750 - 1840) đưa ra vào năm 1786.
Weierstrass
(1815 - 1897)
Như vậy, khái niệm Giới hạn chỉ mới ra đời ở thế kỉ XVII.
Tuy nhiên, tư tưởng "giới hạn" đã xuất hiện rất sớm ở nhiều nhà bác học thời cổ đại.