SGK Đại Số và Giải Tích 11 - Bài 3. Một số phương trình lượng giác thường gặp

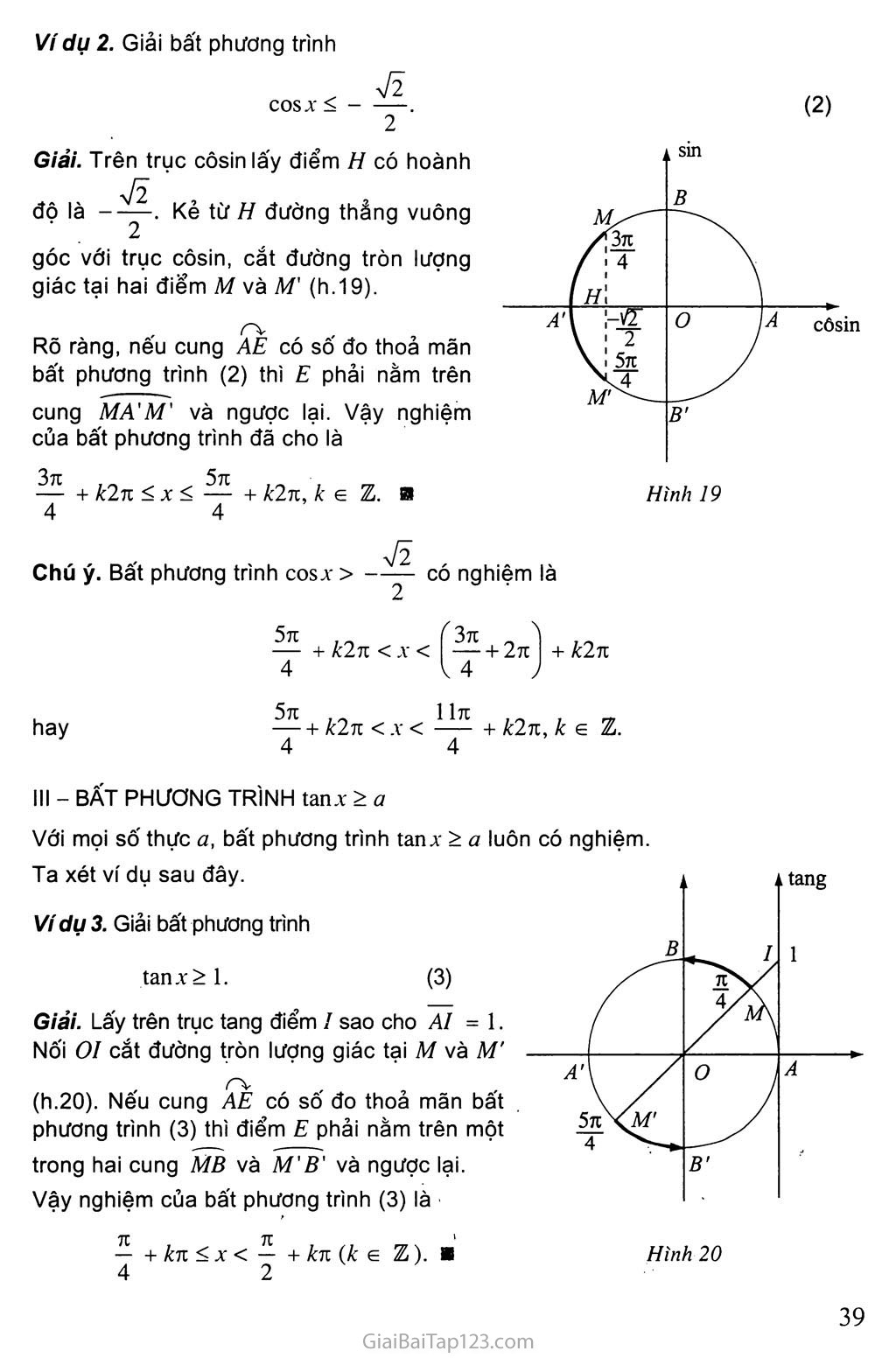
MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
	«	
I - PHƯƠNG TRÌNH BẬC NHAT Đối với một hàm số LƯỢNG GIÁC
Định nghĩa
Phương trình bậc nhất đối với một hàm Số lượng giác là phương trình có dạng
at + b = ồ,	(1)
trong đó a, b là các hằng số (ữ 0) và t là một trong các hàm số lượng giác.
Vídụl
2sinjt - 3 = 0 là phương trình bậc nhất đối với sinx.
73 tan X + 1 = 0 là phương trình bậc nhất đối với tan %.
các phương trình trong Ví dụ 1.
Cách giải
Chuyển vế rồi chia hai vế của phương trình (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.
Ví dụ 2. Giải các phương trình sau :
a)3cosx + 5 = 0;	b) 73 cotx - 3 = 0.
Giải
Từ 3cosx + 5 = 0, chuyển vế ta có
3cosx = -5.	(2)
Chia hai vế của phương trình (2) cho 3, ta được cosx =—-|.
Vì -J < -1 nên phương trình đã cho vô nghiệm.
Từ 73 cotx - 3 = 0, chuyển vế ta có
73 cotx = 3.	(3)
Chia hai vế của phương trình (3) cho 73 , ta được cotx = 73 .
Vì 73 = coty nên cotx = 73 cotx = cot-^ ox = ~ + kn,k<= z. ■ 6 6 6
Phương trình đưa về phương trình bậc nhát đối vói một hàm sô lượng giác
Ví dụ 3. Giải các phương trình sau :
5cosx - 2sin2x = 0 ;	(4)
8sinx cosx Cơs2x =-1.	(5)
Giải
a) Ta có 5cosx - 2sin 2x = 0 5cos X - 4sinx cosx = 0 «• cosx(5 - 4sinx) = 0 cosx = 0
5 - 4sinx = 0.
TI
cosx = 0 X = -- + kĩĩ, k e z. 2
• 5 - 4sinx = 0 . 4sinx = 5 sinx - 4, VÌ 4 > 1 nên phương trình này 4	4
vô nghiệm.
Vậy phương trình (4) có các nghiệm là X = -^ + Ưĩ, £ e z.
b) Ta có
8sinxcosxcos2x =-1 4sin2xcos2x = -1 2sin4x = -1
 sin4x = --7- o 2
4x = —+ k2n
6
. 7tĩ 4x = —- + k2ĩi
6
7t . , K X = ---- + k-y
24	2
7n , Jt X = —— + k—
24	2
(k e Z).
II - PHƯƠNG TRÌNH BẬC HAI ĐÔÌ VỚI MỘT HÀM số LƯỢNG GIÁC
Định nghĩa
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng
at1 + bt + c = 0,
trong đó ữ, b, c là các hằng số (ứ * 0) và t là một trong các hàm số lượng giác.
Ví dụ 4
~ ~ _
2sin X + 3sinx - 2 = 0 là phương trình bậc hai đối với sinx.
2
3cot X - 5cotx - 7 = 0 là phương trình bậc hai đối với cotx.
1 Giải các phương trình sau :
3cos X - 5cosx + 2 = 0;
3 tan2 X - 2 Vĩ tan X + 3 = 0.
Cách giải
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng, ta đưa về việc giải các phương trình lượng giác cơ bản.
Ví dụ 5. Giải phương trình
2sin2 4 + 72sin4 -2 = 0. 2 2
(*),
(1)
Giải. Đặt sin— = t với điều kiện 2
-1<t< 1
ta được phương trình bậc hai theo t
V2
2t2 +4ĩt - 2 = 0.
Phương trình (1) có hai nghiệm tỵ=-yỈ2 và r2 =nhưng chỉ có 72
z2 = —ỹ thoả mãn điều kiện (*). Vậy ta có
. X yÍ2	. X . n
sin— =	 sin— = sin—
2	2	2	4
77 = — + k2ĩi 2	4
X _ 371
77 = —- + k2ĩt
.2	4
X =	+ Mĩĩ
2
X = — + k4ĩi 2
(k g Z).
Phương trình đưa về dạng phương trình bậc hai đối với một hàm số lượng giác 3
Hãy nhắc lại:
Các hằng đẳng thức lượng giác cơ bản ;
Công thức cộng ;
Công thức nhân đôi;
Công thức biến đổi tích thành tổng và tổng thành tích.
Có nhiều phương trình lượng giác mà khi giải có thể đưa về phương trình bậc hai đối với một hàm số lượng giác. Sau đây là một số ví dụ.
Ví dụ 6. Giải phương trình
6cos X + 5sinx -2 = 0.
Giải. Biến đổi coszx = 1 - sin2 X, ta đưa phương trình (2) về dạng
2	.	A
- 6sin X + 5sinx + 4 = 0.
Đặt sin % = t với điều kiện -1 < t < 1, ta được phương trình bậc hai theo t
6? + 5? + 4 = 0.
4	1	,	1
71
Phương trình (3) có hai nghiệm ?! = Ỷ và ?2 = - Ỷ nhưng chỉ có ?2 = - 2 thoả mãn điều kiện. Vậy ta có
sin X - - — sin X = sin - —
K
(k e Z). ■
% = --- + k2n
6
771
%=—-- + k2n 6
Ví dụ 7. Giải phương trình
Ti tanx - ócotx + 2V3 -3 = 0.	(4)
Giải. Điều kiện của phương trình (4) là cosx * 0 và sinx + 0.
Vì cotx = —-— nên phương trình (4) có thể viết dưới dạng tan X
Tĩtanx-—+ 271-3 = 0, tanx
hay	71 tan2x + (273 - 3)tanx -6 = 0.
Đặt tanx = t, ta được phương trình bậc hai theo t
73?2+(273 -3)?-6 = 0.	(5)
Phương trình (5) có hai nghiệm : ?! =73 , ?2 = -2.
Với ?! = 73 ta có tanx = 73 tanx = tan— X = -7- + kĩt, k e z.
3
Với í2 = “2 ta có tanx = -2 o X = arcían(-2) + kĩt, k e z.
Các giá trị này đều thoả mãn điều kiện nêu trên nên chúng là các nghiệm của phương trình (4). ■
s Giải phương trình 3cos26x + 8sin3x cos3x -4 = 0.
Ví dụ 8. Giải phương trình
(6)
. 2 2 ~ 2sin X - 5sinx cosx - cos X = - 2.
Giải. Trước hết, ta thấy nếu COS X = 0 thì phương trình (6) có vế trái bằng 2, còn vế phải bằng -2, nên COS X = 0 không thoả mãn phương trình (6). Vậy COS X 0.
, , 2 N
Vì COSX * 0 nên chia hai vê của phương trình (6) cho COS X, ta được
2tan2x - 5tanx - 1 =	—T-~ 2tan2x - 5tanx - 1 = -2(1 + tan2x).
COS X
Ta đưa được phương trình (6) về phương trình bậc hai theo tanx
2
4tan X - 5tanx + 1 = 0
tan X = 1 1
tanx = —. 4
71
tanx ■- 1 X = -7 + kĩi, k e z.
4
tanx = — X = arctan— + kĩi, k e z.
4
Vậy phương trình (6) có các nghiệm là
và
X = — + kĩi
4
X = arctan— + kn (k e Z). 4
- PHƯƠNG TRÌNH BẬC NHẤT Đối VÓI sin* VÀ cosx
Công thức biến đổi biểu thức asinx + hcosx
^Dựa vào các công thức cộng đã học : sin (ứ + b) = sin acos b + sin bcos a ; sin (ứ - b) = sin acos b - sin bcòs a ;
cos (a + b) = cos ứcos b - sin asin b ; cos (a - Ồ) = cos acos b + sin asin b
va ket qua COS— = sin— = -ỳ-, hãy chứng minh rang :
sinx + cosx= Tĩcos^x-^ ;	b) sinx-cosx= ựĩsin^x-^.
b 	
COS X
= \la
rSĨnx +
Trong trường hợp tổng quát, với ữ2 + b2 * 0, ta có asinx + bcosx
+ bÀ
Vì
a ? f b \la2 + b2 ,	^a2 + b2
\2
+ b )
= cos ỚT,
= 1 nên có một góc a sao cho
b
= sin a.
+ // Vỡ2 + bz
Khi đó asinx + bcosx = ựa2 + ở2 (sin XCOS a + COS X sin a)
of + b2 sin(x + a).
Vậy ta có công thức sau
(1)
với COS a =
và sin a =
+ bÀ
+ bz
asinx + bcosx = v/a2 + b2 sin(x + a),
Phương trình dạng asinx + bcosx = c
Xét phương trình	asinx + bcosx = c,	(2)
với a, b, c e R ; a, b không đồng thời bằng 0 (a2 + b2 0).
Nếu a = 0, b 0 hoặc a * 0, b = 0, phưomg trình (2) có thể đưa ngay về phương trình lượng giác cơ bản. Nếu a * 0, b 0, ta áp dụng công thức (1).
Ví dụ 9. Giải phương trình
sinx + Vs cosx = 1.
Giải. Theo công thức (1) ta có
sinx + V3cosx - ựl + (V3)2 sin(x + á) = 2sin (x + à),
5/3	71
trong đó cos a - 7-, sin a -	. Từ đó lấy a = thì ta có
sin X + V3 cos X = 2 sin ^x + ^.
Khi đó
sin X + 5/3 cos X = 1 2 sin I X + I = 1 sin [ X + 77 ì - 4
l 3;	l 3; 2
71
sin X + — = sin
71 ĩĩ
X + — = -7 + k2n 3	6
X + — = 71 — — + k2n 3	6
7Ĩ
X = - — +'£2ti
6
X = ^ + k2n (k e Z). 2
xá, 6
^Giải phương trình 5/3 sin 3x-COS 3% = >/2.
Bài tập
Giải phương trình
.2	. j_n
sin X - sinx = 0.
Giải các phương trình sau :
2cos2x - 3cosx +1=0;	b) 2sin 2x + V2 sin4x = 0.
Giải các phương trình sau :
a)sin2 4 - 2cos4 + 2 = 0;
2 2 ~
c) 2tan X + 3tanx +1=0;
Giải các phương trình sau :
2sin 2X + sinx cosx - 3cos2x = 0 ;
3sin x-4sinxcosx + 5cos x=2 ;
. 2 . „ „2 1
sin X + sin 2x - 2cos X = — ;
2
2cos2x - 3V3 sin 2x - 4sin2x = - 4.
Giải các phương trình sau :
a) cosx - 5/3 sinx = V2 ;
c) 2sinx + 2cosx - y/2 = 0 ;
Giải các phương trình sau :
a) tan(2x + 1) tan(3x - 1) = 1 ;
b) 8cos2x + 2sinx -7 = 0;
d) tanx - 2cotx +1=0.
b) 3 sin 3x - 4cos 3% = 5 ; d) 5cos2x + 12sin2x - 13 = 0.
b) tan X + tan X + T = 1.
BÀI ĐOC THÊM
TRÌNH LƯỢNG GIÁC
Ta chỉ xét các bất phương trình lượng giác cơ bản. Đó là những bất phương trình dạng sinx > a (hoặc sinx > a, sinx < a, sinx < á), trong đó a là một số thực tuỳ ý. Ta cũng xét những bất phương trình tương tự đối với các hàm số cosx, tanx, cotx.
I - BẤT PHƯƠNG TRÌNH sinx > a
Nếu a > 1 thì bất phương trình sinx > a vô nghiệm, vì sinx < 1 với mọi X.
Nếu a a, vì sinx > -1 với mọi X.
sin
IA côsin
Ta xét trường hợp -1 < a < 1 thông qua ví dụ sau Ví dụ 1. Giải bất phương trình
sinx >	.
2
Giải. Vẽ đường tròn lượng giác tâm o. Trên trục sin lấy điểm K sao cho
— Vĩ _
OK=^ (h.18).
2
Kẻ từ K đường thẳng vuông góc với trục sin, cắt đường tròn tại hai điểm M và M'.
rv
Hình 18
Rõ ràng, nếu cung AD có sô đo thoa mãn bất phương trình (1) thì D phải nằm trên cung MBM' và ngược lại.
Ta có sđ AM = — + k2n, £ e z và
4
. 3ĩi , _	,	„
sđ AM' = —- + k2n, ke í
4
	V2 „
Vậy nghiệm của bất phương trình sinx > -y- là 7Ĩ	3tĩ
— + k2iĩ <x<—+ k2n, k e z. ■
4	4
Chú ý. Điểm cuối của cung có sô' đo là nghiệm của bất phương trình sinx <
phải nằm trên cung M'B'M và ngược lại (h. 18). Khi đó, nghiệm của bất phương trình là
— + k2n < X < (— + 2n I + k2n
3tT	Qjr	
hay	+ k2n < X < -7- + k2n, (k e Z).
4	4
- BẤT PHƯƠNG TRÌNH cosx < a
Nếu a < -1 thì bất phương trình cosx < a vô nghiệm.
Nếu a > 1 thì mọi sô' thựcx đều là nghiệm của bất phương trình cosx < a. Ta xét trường hợp -1 < a < 1 thông qua ví dụ sau đây.
COS X < -
J2.
Ví dụ 2. Giải bất phương trình
Giải. Trên trục côsin lấy điểm H có hoành y/ĩ
độ là	Kẻ từ H đường thẳng vuông
góc với trục côsin, cắt đường tròn lượng giác tại hai điểm M và M' (h. 19).
Rõ ràng, nếu cung AE có sô đo thoả mãn bất phương trình (2) thì E phải nằm trên
cung MA'M' và ngược lại. Vậy nghiệm của bất phương trình đã cho là
+ k2n < X < — + k2n, k e z. ■
- BẤT PHƯƠNG TRÌNH tanx > a
Với mọi số thực a, bất phương trình tanx > a luôn có nghiệm. Ta xét ví dụ sau đây.
Ví dụ 3. Giải bất phương trình
tanx>l.	(3)
Giải. Lấy trên trục tang điểm / sao cho AI = 1.
Nối OI cắt đưòng tròn lượng giác tại M và M’
(h.20). Nêu cung AE có sô đo thoa mãn bất phương trình (3) thì điểm E phải nằm trên một trong hai cung MB và M'B' và ngược lại.
Vậy nghiệm của bất phương trình (3) là
Hình 20
+ kn <x < -^ + kn (k G z). ■
4	2
Chú ý. Nghiệm của bất phương trình tan.v < 1 là
-	+ kn < X <	+ kn, k e
B
J
côtang
/n\
/ 3 \
a\	/
V/
o	ỈA
3
B'
(4)
Hình 21
2	' 4
- BẤT PHƯƠNG TRÌNH cotx < a
Với mọi số thực a, bất phương trình cotx < a đều có nghiệm.
Ta xét ví dụ sau đây.
cot X <
Ví dụ 4. Giải bất phương trình 1
Giải. Lấy điểm J trên trục côtang sao cho
BJ = —Ị=. Nối JO căt đường tròn lượng giác tại V3
hai điểm M và M' (h.21).
Nếu cung AF có số đo thoả mãn bất phương trình (4) thì điểm F phải nằm trên một trong hai cung MA' vàM' A và ngược lại.
Vậy nghiệm của bất phương trình (4) là
4- + kiz < X < n + kn, k e z. ■
3
Chú ý. Nghiệm của bất phương trình cotx>-L.là V3
kn < X < — + kn, k e z.
3