SGK Đại Số và Giải Tích 11 - Bài 2. Hoán vị - Chỉnh hợp - Tổ hợp
HOÁN VỊ - CHỈNH HỢP - Tổ HỢP
- HOÁN VỊ
Định nghĩa
Ví dụ 1. Trong một trận bóng đá, sau hai hiệp phụ hai đội vẫn hoà nên phải thực hiện đá luân lưu 11 m. Một đội đã chọn được năm cầu thủ để thực hiện đá năm quả 11 m. Hãy nêu ba cách sắp xếp đá phạt.
Giải. Để xác định, ta giả thiết tên của năm cầu thủ được chọn là A, B, c, D, E. Để tổ chức đá luân lưu, huấn luyện viên cần phân công người đá thứ nhất, thứ hai, ... và kết quả phân công là một danh sách có thứ tự gồm tên của năm cầu thủ. .Chẳng hạn, nếu viết DEACB nghĩa là D đá quả thứ nhất, E đá quả thứ hai, ... và B đá quả cuối cùng.
Có thể nêu ba cách tổ chức đá luân lưu như sau :
Cách 1 : ABCDE.
Cách 2 : ACBDE.
Cách 3 : CABED. ■
Mỗi kết quả của việc sắp thứ tự tên của năm cầu thủ đã chọn được gọi là một hoán vị tên của năm cầu thủ.
ĐỊNH NGHĨA
Cho tập hợp A gồm n phần tử (« > 1).
Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
1
Hãy liệt kê tất cả các số gồm ba chữ sô' khác nhau từ các chữ số 1, 2, 3.
NHẬN XÉT
r ■ ■ '
Hai hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp.
Chẳng hạn, hai hoán vị abc và acb của ba phần tử a, b, c là khác nhau.
Số các hoán vị
Ví dụ 2. Có bao nhiêu cách sắp xếp bốn bạn An, Bình, Chi, Dung ngồi vào một bàn học gồm bốn chỗ ?
Giải. Để đơn giản, ta viết A, B, c, D thay cho tên của bốn bạn và viết ACBD để mô tả cách xếp chỗ như Hình 27.
Cách thứ nhất: Liệt kê. Hinh 77
Các cách sắp xếp chỗ ngồi được liệt kê như sau :
ABCD, ABDC, ACBD, ACDB, ADBC, ADCB,
BACD, BADC, BCAD, BCDA, BDAC, BDCA,
CABD, CADB, CBAD, CBDA, CDAB, CDBA,
DACB, DABC, DBAC, DBCA, DCAB, DCBA.
Như vậy có 24 cách, mỗi cách cho ta một hoán vị tên của bốn bạn và ngược lại.
b) Cách thứ hai: Dùng quy tắc nhân.
Có bốn cách chọn một trong bốn bạn để xếp vào chỗ thứ nhất.
Sau khi đã chọn một bạn, còn ba bạn nữa. Có ba cách chọn một bạn xếp vào chỗ thứ hai.
Sau khi đã chọn hai bạn rồi còn hai bạn nữa. Có hai cách chọn một bạn ngồi vào chỗ thứ ba.
Bạn còn lại được xếp vào chỗ thứ tư.
Theo quy tắc nhân, ta có số cách xếp chỗ ngồi là 4.3.2.1 = 24 (cách). ■
Kí hiệu p„ là số các hoán vị của n phần tử. Ta có định lí sau đây.
ĐỊNH LÍ
•»
p„ = «(«-!)... 2.1.
Chứng minh. Để lập được mọi hoán vị của n phần tử, ta tiến hành như sau : Chọn một phần tử cho vị trí thứ nhất. Có n cách.
Sau khi chọn một phần tử cho vị trí thứ nhất, có n - 1 cách chọn một phần tử cho vị trí thứ hai.
Sau khi đã chọn rt - 2 phần tử cho n - 2 vị trí đầu tiên, có hai cách chọn một trong hai phần tử còn lại để xếp vào vị trí thứ n - 1.
Phần tử còn lại sau cùng được xếp vào vị trí thứ n.
Như vậy, theo quy tắc nhân, có n.(n - 1) ... 2.1 kết quả sắp xếp thứ tự n phần tử đã cho.
Vậy
p„ = « («- 1)... 2.1. ■
CHƯ Y
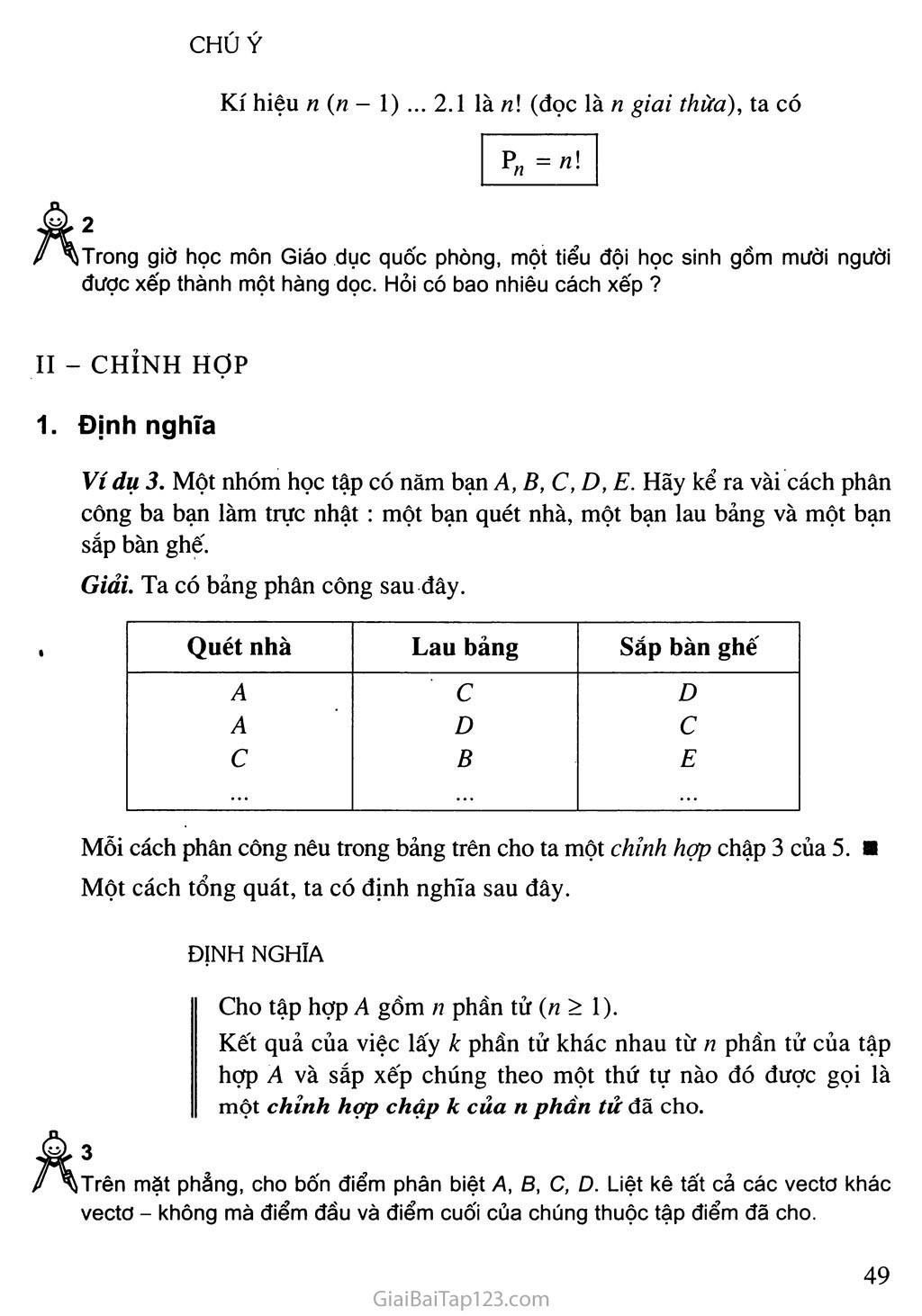
Kí hiệu n {n - 1) ... 2.1 là n\ (đọc là n giai thừa), ta có
p„ = n!
ln II;
Trong giờ học môn Giáo dục quốc phòng, một tiểu đội học sinh gồm mười người được xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp ?
- CHỈNH HỢP
Định nghĩa
Ví dụ 3. Một nhóm học tập có năm bạn A,B,C,D,E. Hãy kể ra vài cách phân công ba bạn làm trực nhật : một bạn quét nhà, một bạn lau bảng và một bạn sắp bàn ghế.
Giải. Ta có bảng phân công sau đây.
Quét nhà
Lau bảng
Sáp bàn ghê
A
c
D
A
D
c
c
B
E
Mỗi cách phân công nêu trong bảng trên cho ta một chỉnh hợp chập 3 của 5. ■ Một cách tổng quát, ta có định nghĩa sau đây.
ĐỊNH NGHĨA
Cho tập hợp A gồm n phần tử (/7 > 1).
Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh họp chập k của n phần tử đã cho.
Trên mặt phẳng, cho bốn điểm phân biệt A, B, c, D. Liệt kê tất cả các vectơ khác vectơ - không mà điểm đầu và điểm cuối của chúng thuộc tập điểm đã cho.
Sô các chỉnh hợp
'Trở lại Ví dụ 3, ngoài cách tính sô' cách phân công trực nhật bằng phương pháp liệt kê, ta còn có một cách khác là sử dụng quy tắc nhân. Để tạo nên mọi cách phân công, ta tiến hành-như sau :
Chọn một bạn từ năm bạn để giao việc quét nhà. Có 5 cách.
Khi đã chọn một bạn quét nhà rồi, chọn tiếp một bạn từ bốn bạn còn lại để giao việc lau bảng. Có 4 cách.
Khi đã có các bạn quét nhà và lau bảng rồi, chọn một bạn từ ba bạn còn lại để giao việc sắp bàn ghế. Có 3 cách.
Theo quy tắc nhân, số cách phân công trực nhật là 5.4.3 = 60 (cách).
Nói cách khác, ta có 60 chỉnh hợp chập 3 của 5 bạn. ■
Kí hiệu là số các chỉnh hợp chập k của 77 phần tử (1 < £ < 77). Ta có định lí sau đây.
ĐỊNH LÍ
= 77(77 - 1)... (77 - k + 1).
( >
Chứng minh. Để tạo nên mọi chỉnh hợp chập k của n phần tử, ta tiến hành như sau :
Chọn một trong n phần tử đã cho xếp vào vị trí thứ nhất. Có n cách.
Khi đã có phần tử thứ nhất, chọn tiếp một trong 77-1 phần tử còn lại xếp vào vị trí thứ hai. Có /7 - 1 cách.
Sau khi đã chọn k - 1 phần tử rồi, chọn một trong 77 - (k - 1) phần tử còn lại xếp vào vị trí thứ k. Có 77 - k -Ị^l cách.
Từ đó theo quy tắc nhân, ta được
A^ = 77(7? - 1)...(77 - k + 1). ■
Ví dụ 4. Có bao nhiêu số tự nhiên gồm năm chữ số khác nhau được lập từ các chữ số 1, 2,..., 9 ?
Giải. Mỗi số tự nhiên có năm chữ số khác nhau được lập bằng cách lấy năm chữ số khác nhau từ chín chữ số đã cho và xếp chúng theo một thứ tự nhất định. Mỗi số như vậy được coi là một chỉnh hợp chập 5 của 9. Vậy số các số đó là
Aọ = 9.8.7 . &. 5 = 15 120. ■
CHÚ Ý
Với quy ước 0! = 1, ta có
-—'-■■■ ■— > 1 < k < n.
(n - k)
Mỗi hoán vị của 1Ỉ phần tử cũng chính là một chỉnh hợp chập n củá n phần tử đó. Vì vậy
- TỔ HỢP
Định nghĩa
Ví dụ 5. Trên mặt phẳng, cho bốn điểm phân biệt A, B, c, D sao cho không có ba điểm nào thẳng hàng.'Hỏi có thể tạo nên bao nhiêu tam giác mà các đỉnh thuộc tập bốn điểm đằ cho ?
Giải. Mỗi tam giác ứng với một tập con gồm ba điểm từ tập bốn điểm đã cho. Vậy ta có bốn tam giác ABC, ABD, ACD, BCD. ■
Một cách tổng quát, ta có định nghĩa sau đây.
ĐỊNH NGHĨA
Giả sử tập A có n phần tử (« > 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.
CHÚ Ý
Số k trong định nghĩa cần thoả mãn điều kiện 1 < k < n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tập rỗng là tổ hợp chập 0 của n phần tử.
/ ^Cho tập A = {1,2, 3,4, 5}. Hãy liệt kê các tổ hợp chập 3, chập 4 của 5 phần tử của A.
Số các tổ hợp
Kí hiệu là số các tổ hợp chập k của n phần tử (0 k k < rì). Ta có định lí sau đây.
ĐỊNH LÍ
ck =
n\
kl(n - ky.
Chứng minh. Với k = 0, công thức hiển nhiên đúng.
Với £ > 1, ta thấy một chỉnh hợp chập k của n phần tử được thành lập như sau :
Chọn một tập con k phần tử của tập hợp gồm n phần tử. Có c^ cách chọn.
Sắp thứ tự k phần tử chọn được. Có k\ cách.
Vậy theo quy tắc nhân, ta có số các chỉnh hợp chập k của n phần tử là = c^ .£!
Từ đó c„ =
nỉ
kỉ kỉ(n-ky.
Ví dụ 6. Một tổ eó 10 người gồm 6 nam và 4 nữ. Cần lập một đoàn đại biểu gồm 5 người. Hỏi:
Có tất cả bao nhiêu cách lập ?
Có bao nhiêu Cách lập đoàn đại biểu, trong đó có ba nam, hai nữ ?
Giải
Mỗi đoàn được lập là một tổ hợp chập 5 của 10 (người). Vì vậy, số đoàn đại biểu có thể có là
cfo = = 252.
10 5!5!
Chọn 3 người từ 6 nam. Có Cg cách chọn.
Chọn 2 người từ 4 nữ. Có C4 cách chọn.
Theo quy tắc nhân, có tất cả Cg.cị = 20.6 = 120 cách lập đoàn đại biểu gồm ba nam và hai nữ. ■
^Có 16 đội bóng đá tham gia thi đấu. Hỏi cần phải tổ chức bao nhiêu trận đấu sao cho hai đội bất kì đều gặp nhau đúng một lần ?
Tính chất của các số cj
Từ định lí về công thức tính số các tổ hợp chập k của n phần tử, ta có các tính chất sau đây.
Tính chất 1
ự\k r-ììĩ—k
(0 < k< rí).
Chẳng hạn, C7 = C7 = 35. b) Tính chất 2 (công thức Pa-xcan)
(~'k~Ị I C'k
C/7-l + c
/7—1
(1 < k < n).
Chẳng hạn, C7 + C7 = Cg = 70.
Ví dụ 7. Chứng minh rằng, với 1<k<n-2, ta có
'n '~'n-2
Giải. Theo Tính chất 2, ta có
c
+ c«-2 '
,k-2
n-2
4- -
+ C?-2 -
fdc-l ~ Ci-l ’
(1)
,k-ỉ
n-2
+ C«-2 =
c^
c«-l-
(2)
Cộng các vế tương ứng của (1) và (2) và theo Tính chất 2, ta có ik _ r'k — X , r^k
c‘:ỉ + 2c‘-‘
n-2 + ''-'n-2 - Cỉ-1 + Cỉ-1 •
BÀI ĐỌC THÊM
tì
TÍNH SỐ CÁC HOÁN VỊ VÀ số CÁC Tổ HỢP BẰNG MÁY TÍNH Bỏ TÚI
Có thể sử dụng máy tính bỏ túi để tính số các hoán vị nỉ và số các tổ hợp ck .
Tính số các hoán vị bằng máy tính bỏ túi
Dùng máy tính bỏ túi CASIO fx - 500MS để tính «!, ta ấn các phím theo trình tự sau :
SHIFT x!
Ấn SỐ n, ấn phím MBB, ấn phím IỊịỊBMể), ấn phím MB. Khi đó, kết quả sẽ hiển thị ở dòng thứ hai.
Ví dụ 1. Tính 10!.
SHIFT x!
Ta bấm liên tiếp các phím sau :
Dòng thứ hai hiện ra 3,628,800.
Vậy 10! = 3 628 800.
Tính sô' các tổ hợp bằng máy tính bỏ túi
Dùng máy tính bỏ túi CASIO fx - 500 MS để tính C” , ta ấn các phím theo trình tự sau :
Ấn số n, ấn phím MSáB, ấn sô' k, ấn phím BBB. Kết quả hiển thị ở dòng thứ hai. Ví dụ 2. Tính c^2 .
Ta ấn liên tiếp các phím sau :
Dòng thứ hai hiện ra 792. Vậy cf2 = 792.
Bài tạp
»
Từ các chữ số 1, 2, 3, 4, 5, 6, lập các số tự nhiên gồm sáu chữ số khác nhau. Hỏi:
Có tất cả bao nhiêu số ?
Có bao nhiêu số chẵn, bao nhiêu số lẻ ?
Có bao nhiêu số bé hơn 432 000 ?
Có bao nhiêu cách sắp xếp chỗ ngồi cho mười người khách vào mười ghế kê thành một dãy ?
Giả sử có bảy bông hoa màu khác nhau và ba lọ khác nhau. Hỏi có bao nhiêu cách cắm ba bông hoa vào ba lọ đã cho (mỗi lọ cắm một bông) ?
Có bao nhiêu cách mắc nối tiếp 4 bóng đèn được chọn từ 6 bóng đèn khác nhau ?
Có bao nhiêu cách cắm 3 bông hoa vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông) nếu :
Các bông hoa khác nhau ?
Các bông hoa như nhau ?
Trong mặt phẳng, cho sáu điểm phân biệt sao cho không có ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho ?
Trong mặt phẳng có bao nhiêu hình chữ nhật được tạo thành từ bốn đường thẳng song song với nhau và năm đường thẳng vuông góc với bốn đường thẳng song song đó ?