SGK Đại Số và Giải Tích 11 - Bài 5. Xác suất của biến cố

XÁC SUẤT CỦA BIẾN CỐ
I - ĐỊNH NGHĨA cổ ĐIÊN của xác suất
Định nghĩa
Một đặc trưng định tính quan trọng của biến cố liên quan đến một phép thử là nó có thể xảy ra hoặc không xảy ra khi phép thử đó được tiến hành. Một câu hỏi được đặt ra là nó có xảy ra không ? Khả năng xảy ra của nó là bao nhiêu ? Như vậy, nảy sinh một vấn đề là cần phải gắn cho biến cố đó một con số hợp lí để đánh giá khả năng xảy ra của nó. Ta gọi số đó là xác suất của biến cố.
Ví dụ 1. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Các kết quả có thể là (h.33)
Hình 33
Không gian mẫu của phép thử này có sáu phần tử, được mô tả như sau Q = {1,2, 3, 4, 5,6}.
Do con súc sắc là cân đối, đồng chất và được gieo ngẫu nhiên nên khả năng xuất hiện từng mặt của con súc sắc là như nhau. Ta nói chúng đồng
khả năng xuất hiện. Vậy khả năng xuất hiện của mỗi mặt là y.
6
Do đó, nếu A là biến cố : "Con súc sắc xuất hiện mặt lẻ" (A - {1, 3, 5}) thì khả năng xảy ra của A là
J_ 1	1 _ 3 _ j
6 + 6 + 6 - 6 - 2’
số này được gọi là xác suất của biến cố A.
1
Từ một hộp chứa bốn quả cầu ghi chữ a, hai quả cầu ghi chữ b và hai quả cầu ghi chữc (h.34), lấy ngẫu nhiên một quả. Kí hiệu :
A : "Lấy được quả ghi chữ a";
B : "Lấy được quả ghi chữ b"; c : "Lấy được quả ghi chữc".
Có nhận xét gì về khả năng xảy ra của các biến cố Â, B và c ? Hãy so sánh chúng với nhau.
Q 0 0 0 © ® Q 0
Hình 34
Một cách tổng quát, ta có định nghĩa sau đây.
ĐỊNH NGHĨA
Giả sử A là biến cố liên quan đến một phép thử với không gian mẫu o chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện.
Ta gọi tỉ số ' là xác suất của biến CỐA, kí hiệu là P(Â).
/?(Q)
CHÚ Ý
/2(A) là số phần tử của A hay cũng là số các kết quả thuận lợi cho biến cố A, còn n(Q) là số các kết quả có thể xảy ra của phép thử.
Ví dụ
Ví dụ 2. Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất hai lần. Tính xác suất của các biến cố sau :
A : "Mặt sấp xuất hiện hai lần" ;
B : "Mặt sấp xuất hiện đúng một lần" ;
c : "Mặt sấp xuất hiện ít nhất một lần".
Giải (h.35). Không gian mẫu Q = {SS, SN, NS, NN} gồm bốn kết quả. Vì đồng tiền cân đối, đồng chất và việc gieo là ngẫu nhiên nên các kết quả đồng khả năng xuất hiện. Ta có
A = {ss}, rt(/4) = 1, rt(Q) = 4, theo định nghĩa ta có
*ss
*SN
*NS
*NN
n/AX «(4)	1	Q
P(Â) =	= - .	Hình 35.
n(fi) 4
£= {SV, VS}, n(£) = 2nên
r(B)=^4 1 n(Q) 4	2
3
c = {ss, SN, NS}, n(C) = 3 nên
Ví dụ 3. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Tính xác suất của các biến cố sau :
A : "Mặt chẵn xuất hiện" ;
B : "Xuất hiện mặt có số chấm chia hết cho 3" ; c : "Xuất hiện mặt có số chấm không bé hơn 3".
•
•
•
•
•
•
• •
• •
• •
•
• •
• •
• •
• •
Hình 36
Giải. Không gian mẫu có dạng : Q - {1, 2, 3, 4, 5, 6), gồm sáu kết quả đồng khả năng xuất hiện (h.36). Rõ ràng
A = {2, 4,6}, £={3,6}, c=. {3,4,5,6},
«(Â) = 3, «(£) = 2, «(C) = 4.
2-1 6 " 2’
P(A) =
«(Q)
Từ đó, theo định nghĩa ta có /ỉ(Â)
P(B) =
n(fì)
P(C) =
2 _Ị_
6 - 3 ’
4	2
-T = T-. ■
6	3
Ví dụ 4. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần. Tính xác suất của các biến cố sau :
A : "Số chấm trong hai lần gieo bằng nhau" ;
B : "Tổng số chấm bằng 8".
Giải. Như đã biết (xem Ví dụ 3, §4), Q = {(z, ỹ) I 1 < i,j <6}, gồm 36 kết quả đồng khả năng xuất hiện. Ta có bảng (xem thêm Hình 29) :
X
1
2
3
4
5
6
1
\ll
\L2
13
14
15
16
2
21s
\2z
\23
24
25/
Xw
3
31
32s
\3.v
\34/
'33/
/36
4
41
42
43>
<45
46
5
51
52/
Xx
.5X
\56
6
61
<62/
/63
64
6iX
\6V
A = {(1, 1), (2, 2), (3, 3), (4, 4), (5,5), (6, 6)}, «(A) = 6, n(Q) = 36. Từ đó, theo định nghĩa ta có
- TÍNH CHẤT CỦA XÁC SUẤT
Định lí
Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, ta có định lí sau đây.
ĐỊNH LÍ
P(0) = o, P(fì)= 1.
0 < P(A) < 1, với mọi biến cố A.
Nếu A và B xung khắc, thì
P(A u B) = P(A) + P(B) {công thức cộng xác suấtỵ J
Â2
7 NChứng minh các kết luận a), b) và c) của định lí.
HỆ QUẢ
Với mọi biến cố A, ta có
P(Ã)= 1 -P(A).
V	;	
7
Chứng minh. Vì A u A = Q, và A n A - 0 nên theo công thức cộng xác suất ta có
1 = P(Q)=P(A) + p(Ã).
Từ đó ta có điều phải chứng minh. ■
Ví dụ
ooo
Ví dụ 5. Từ một hộp chứa ba quả cầu trắng, hai quả cầu đen (h.37), lấy ngẫu nhiên đồng thời hai quả. Hãy tính xác suất sao cho hai quả đó :
Khác màu ; b) Cùng màu.	Hình 37
Giải. Mỗi lần lấy đồng thời hai quả cầu cho ta một tổ hợp chập hai của năm phần tử. Do đó, không gian mẫu gồm các tổ hợp chập hai của năm phần tử và «(Q) = c| =10.
Vì việc lấy quả cầu là ngẫu nhiên nên các kết quả đó đồng khả năng.
Kí hiệu A : "Hai quả khác màu", B : "Hai quả cùng màu".
Vì chỉ có hai màu đen hoặc trắng nên ta thấy ngay B = A .
Theo quy tắc nhân, n(A) = 3.2 = 6.
Do đó
P(A) = ^ = ± = |
n(fì) 10	5
Vì B = À nên theo hệ quả ta có
P(B) = P(Ã) = 1 - P(A) = I. ■
Ví dụ 6. Một hộp chứa 20 quả cầu đánh số từ 1 đến 20. Lấy ngẫu nhiên một quả. Tính xác suất của các biến cố sau :
A : "Nhận được quả cầu ghi số chẵn" ;
B : "Nhận được quả cầu ghi số chia hết cho 3 ;
A n B ;
c : "Nhận được quả cầu ghi số không chia bết cho 6".
Giải. Không gian mẫu được mồ tả là = {1, 2, ..., 20} gồm 20 kết quả đồng khả năng, n(Q) = 20.
A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, /ĩ(A) = 10 nên
P(A) = ^ = i£ 1 n(Q) 20	2
B= {3, 6, 9, 12, 15, 18}, n(B) = 6.
Từ đó
P(B) =	= Á = 3
«(Q)	20	10
c)VìAnB = {6, 12, 18}, n(A n 5) = 3 nên
P(A n B) =
n(A n g)
n(Q)
_3_
20
Vì A n B = {6, 12, 18}, nên A n B là biến cố : "Nhận được quả cầu ghi số chia hết cho 6". Do đó, c là biến cố đối của biến cố A B, ta có c = A n B và
P(C)= 1 -P(AnB)= 1
17
-ị. ■ 20
Ill
- CÁC BIẾN CỐ ĐỘC LẬP, CÔNG THỨC NHÂN XÁC SUẤT
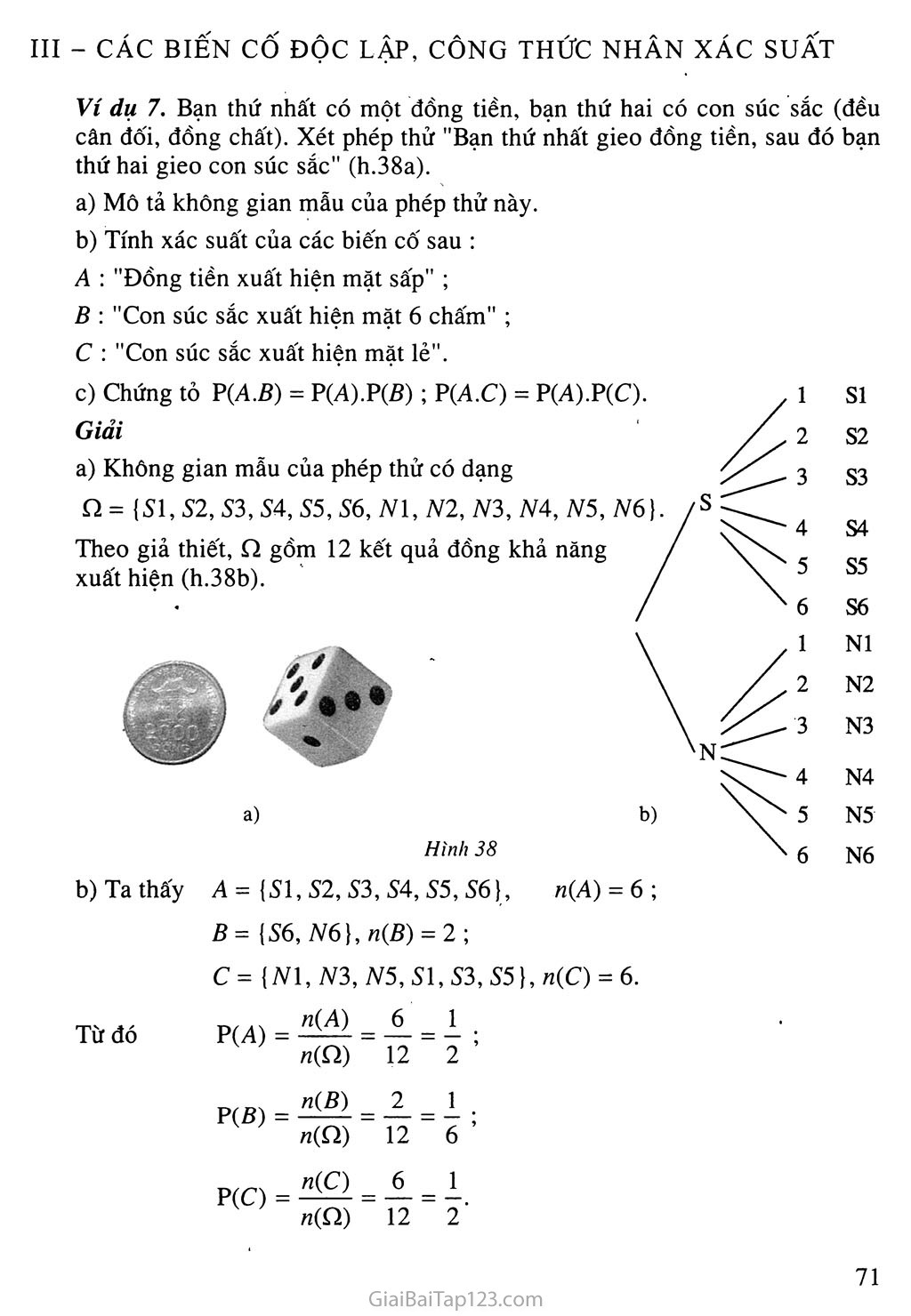
Ví dụ 7. Bạn thứ nhất có một đồng tiền, bạn thứ hai có con súc sắc (đều cân đối, đồng chất). Xét phép thử "Bạn thứ nhất gieo đồng tiền, sau đó bạn thứ hai gieo con súc sắc" (h.38a).
Mô tả không gian mẫu của phép thử này.
Tính xác suất của các biến cố sau :
A : "Đồng tiền xuất hiện mặt sấp" ;
B : "Con súc sắc xuất hiện mặt 6 chấm" ;
c : "Con súc sắc xuất hiện mặt lẻ".
Chứng tỏ P(A.B) = P(A).P(B) ; P(A.C) = P(A).P(C).
Giải
Không gian mẫu của phép thử có dạng
Q = {SI, S2, S3, S4, S5, S6, Nỉ, N2, N3, NA, N5, N6}
Theo giả thiết, gồm 12 kết quả đồng khả năng xuất hiện (h.38b).
a)
Hình 38
Ta thấy A = {SI, S2, S3, S4, S5, S6},	«(A) = 6 ;
B= jS6, N6(,«(B) = 2;
C={NỈ,N3, (V5,S1,S3,S5},«(C) = 6.
Từ đó
_Ị_
n(A) 
6
«(Q) =
12
«(£) 
2
«(íl) =
12
«(C) 
6
«(fì)
12
P(A) =
P(B) =
P(C) =
6
J_
2'
2 ;
Rõ ràng A.B = {S6 Ị và P(Â.fi) =
n(A.B)
Ta có
P(Â.B) = -^- = ^.- = P(Â)P(£). 12 2 6
Tương tự, A.c = {SI, S3, S5| ;
P(AC) =
Trong Ví dụ 7, ta nhận thấy xác suất xuất hiện mỗi mặt của con súc sắc là ỳ, 6
không phụ thuộc vào việc đồng tiền xuất hiện mặt "sấp" hoặc "ngửa".
Nếu sự xảy ra của một biến cố không ảnh hưởng đến xác suất xảy ra của một biến cố khác thì ta nói hai biến cố đó độc lập. Như vậy, trong Ví dụ 7, các biến cố A và B độc lập và cũng vậy, A và c độc lập.
Tổng quát, đối với hai biến cố bất kì ta có mối quan hệ sau : ,
A và B là hai biến cố độc lập khi và chỉ khi
P(Â.B) = P(Ạ).P(B).
:>
BÀI ĐOC THÊM
MỞ RỘNG QUY TẮC CỘNG VÀ CÔNG THỨC CỘNG XÁC SUẤT
Quy tắc cộng còn được mở rộng đổi với các tập hợp hữu hạn, có giao khác rỗng. Có thể chứng minh được rằng, với hai tập hợp hữu hạn A và B bất kì, ta có
í
n(A u B) = /ỉ(A) + /;(Z?) - /i(A n B) (quy tắc bao hàm và loại trừ).
Ví dụ 1. Một tổ mười người sẽ được chơi hai môn thể thao là cầu lông và bóng bàn. Có năm bạn đăng kí chơi cầu lông, bốn bạn đăng kí chơi bóng bàn, trong đó có hai bạn đăng kí chơi cả hai môn. Hỏi có bao nhiêu bạn đăng kí chơi thể thao ? Bao nhiêu bạn không đăng kí chơi thể thao ?
Giải. Kí hiệu X là tập hợp các học sinh trong tổ ; A là tập hợp các học sinh đăng kí chơi cầu lông, B là tập hợp các học sinh đăng kí chơi bóng bàn (h.39), thế thì «(Ầ) = 10, «(Â) = 5, 77(B) = 4, 7?(Ẩ nB) = 2. Như vậy :
A u B là tập hợp các bạn đăng kí chơi thể thao. Vì n(A n B) = 2 nên số bạn đăng kí chơi thể thao là n(A uB) = 71(A) + 7?(B) - n(A n B) =5+4-2=7 (bạn)
( 5 i
ỆH4
\A
X
Từ đó, số bạn không đăng kí chơi môn thể thao nào là	39
iì(X) - «(A uB) = 10-7 = 3 (bạn). ■
Nhờ quy tắc cộng mở rộng, ta có công thức cộng xác suất mở rộng sau đây.
Với hai biến cố 4 và 6 bất kì cùng liên quan đến một phép thử, ta có
P(A u B) = P(A) + P(B) - P(A.B).
Ví dụ 2. Gieo ngẫu nhiên một con súc sắc cân đối đồng chất hai lần. Tính xác suất của các biến cố sau :
A : "Lần thứ nhất xuất hiện mặt 6 chấm" ;
B : "Lần thứ hai xuất hiện mặt 6 chấm" ; c : "ít nhất một lần xuất hiện mặt 6 chấm" ;
D : "Không lần nào xuất hiện mặt 6 chấm".
Giải. Ta	có	Q =	{(/,ý) 11 < i,j	< 6}, trong đó i là số chấm	xuất	hiện	trong lần gieo
thứ nhất,	j là sô'	chấm xuất hiện	trong lấn gieo thứ hai,	n(Q)	=	36. Như vậy
A = {(6, j) I 1	<;< 6}, /ỉ(A) = 6 ;
B= {(/, 6) I 1	<7 <6), /;(B) = 6 ;
c = A u B, £>= C,AnB= {(6, 6)Ị,/?(AnB) = 1. Từ đó, theo định nghĩa ta có
P(A)=^=± 1 P(B)=^ = Á >
P(A.B) =
7i(AnB)_ 1 /?(Í2)	36
Theo nhận xét ta có
7?(Q)	36	6	/?(Í2)	36	6
P(C) = P(A u B) = P(A) + P(B) - P(A. B) = | +
6	6	56
Theo hệ quả ta có
P(D)= P(C) = 1 -P(C) = 1-^1 = II 36	36
Bài tập
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần.
Hãy mô tả không gian mẫu.
Xác định các biến cố sau :
A : "Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10" ;
B : "Mặt 5 chấm xuất hiện ít nhất một lần".
Tính P(Â), P(B).
Có bốn tấm bìa được đánh số từ 1 đến 4. Rút ngẫu nhiên ba tấm.
Hãy mô tả không gian mẫu.
Xác định các biến cố sau :
A : "Tổng các số trên ba tấm bìa bằng 8" ;
B : "Các số trên ba tấm bìa là ba số tự nhiên liên tiếp".
Tính P(Ẩ), P(B).
Một người chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác nhau. Tính xác suất để Hai chiếc chọn được tạo thành một đôi.
Gieo một con súc'sắc cân đối và đồng chất. Giả sử con súc sắc xuất hiện mặt b chấm. Xét phương trình X + bx + 2 = 0. Tính xác suất sao cho :
Phương trình có nghiệm ;
Phương trình vô nghiệm ;
Phương trình có nghiệm nguyên.
Từ cỗ bài tú lơ khơ 52 con, rút ngẫu nhiên cùng một lúc bốn con. Tính xác suất sao cho :
Cả bốn con đều là át;
Được ít nhất một con át;
Được hai con át và hai con K.
Hai bạn nam và hai bạn nữ được xếp ngồi ngẫu nhiên vào bốn ghế xếp thành hai dãy đối diện nhau. Tính xác suất sao cho :
Nam, nữ ngồi đối diện nhau ;
Nữ ngồi đối diện nhau.
Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa 6 quả trắng, 4 quả đen. Hộp thứ hai chứa 4 quả trắng, 6 quả đen. Từ mỗi hộp lấy ngẫu nhiên một quả. Kí hiệu :
A là biến cố : "Quả lấy từ hộp thứ nhất trắng" ;
B là biến cố : "Quả lấy từ hộp thứ hai trắng".
Xét xem A và B có độc lập không.
Tính xác suất sao cho hai quả cầu lấy ra cùng màu.
Tính xác suất sao cho hai quả cầu lấy ra khác màu.
BÀĨ ĐỌC THÊM
ĐỊNH NGHĨA THỐNG KÊ CỦA XÁC SUẤT
Một đồng tiền cân đối và đồng chất được gieo n lần. Kí hiệu ns là số lần xuất hiện mặt sấp s trong n lần gieo đó.
Ta gọi tỉ số / (5) - — là fan suất xuất hiện mặt sấp trong n lần gieo.
. rì
Bằng thực nghiệm ta thấy, tần suất thay đổi khi ta thực hiện loạt n lần gieo khác cũng như khi tăng số lần gieo.
Tuy nhiên với n khá lớn, tần suất này có tính ổn định, nghĩa là nó dao động xung quanh sô' i và khi n tăng, tần suất ngày càng gần số y
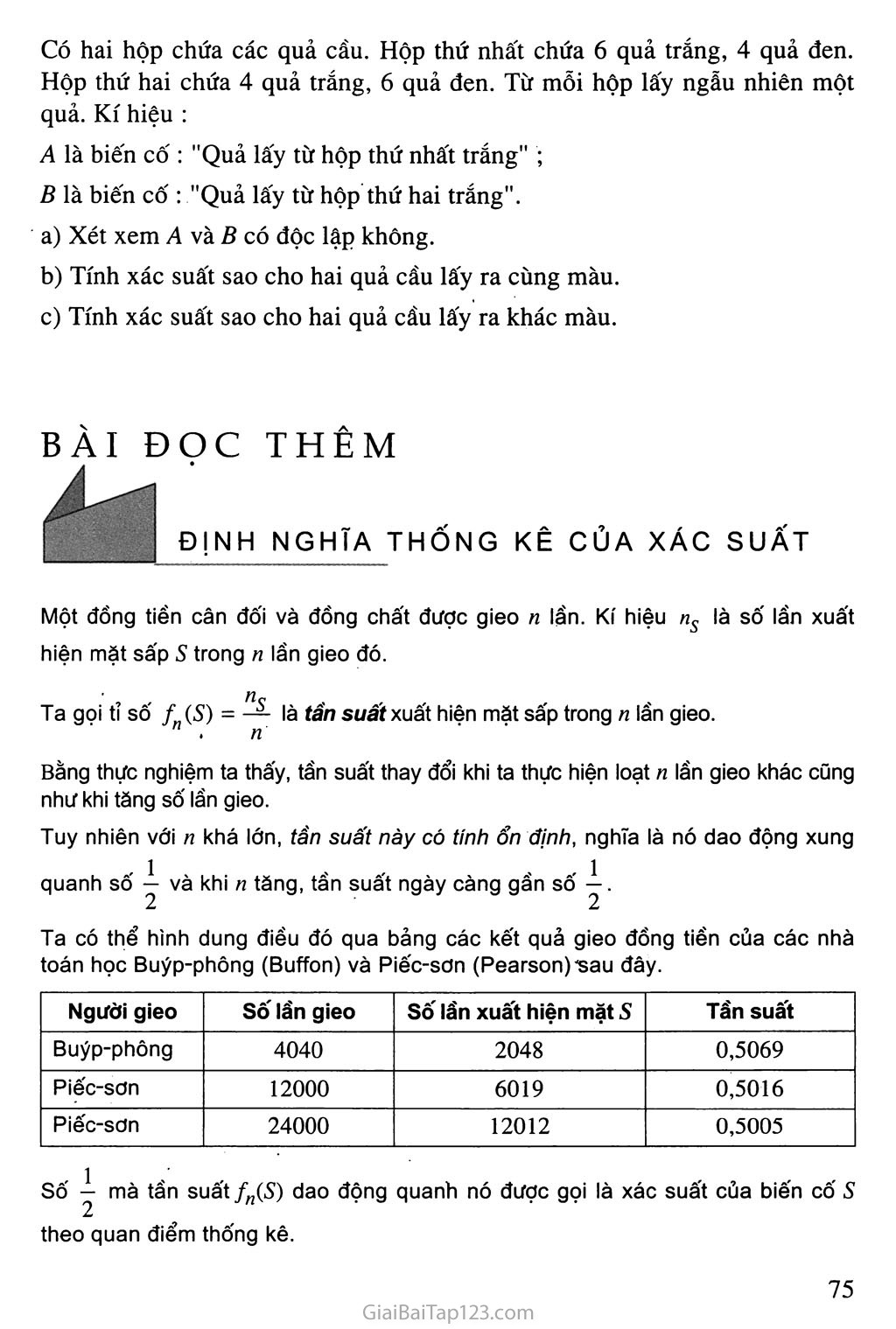
Ta có thể hình dung điều đó qua bảng các kết quả gieo đồng tiền của các nhà toán học Buýp-phông (Buffon) và Piếc-sơn (Pearson) sau đây.
Người gieo
Số lần gieo
Số lần xuất hiện mặt 5
Tần suất
Buýp-phông
4040
2048
0,5069
Piếc-sơn
12000
6019
0,5016
Piếc-sơn
24000
12012
0,5005
Sô' y mà tần suất/„(S) dao động quanh nó được gọi là xác suất của biến cô' s theo quan điểm thống kê.
Một cách tổng quát:
Kí hiệu «4 là số lần xuất hiện biến cô' A trong một dãy n phép thử
được lặp đi lặp lại (dãy các phép thử lặp). Tỉ sô' — gọi là tẩn suất n
xuất hiện biến cô A.
Khi n tăng, — ngày càng gần một sô' P(Â) xác định. Người ta gọi
n
sô' P(A) đó là xác suất của biến cốA theo quan điểm thông kê.
Trong trường hợp phép thử chỉ có một sô' hữu hạn kết quả đồng khả năng xuất hiện thì số P(Â) trong định nghĩa này trùng với sô' P(Â) trong định nghĩa cổ điển của xác suất. Do đó, định nghĩa thống kê của xác suất là một sự mở rộng thực sự của định nghĩa cổ điển của xác suất.
Nhà toán học Thuỵ Sĩ J.Béc-nu-li (Jacob Bernoulli) là người đầu tiên phát hiện ra
nA
tính ôn định thông kê của dãy tân suất —.
n
Poát-xông (Poisson) là người đầu tiên gọi quy luật ổn định của tần suất là luật số lớn.