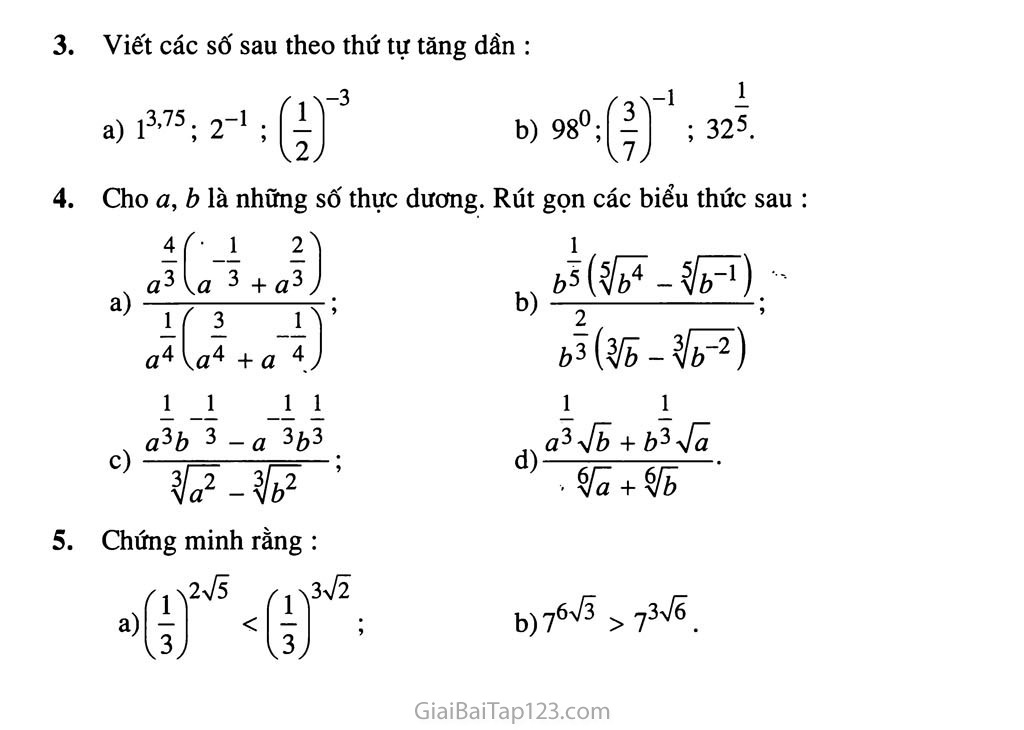SGK Giải Tích 12 - Bài 1. Lũy thừa

Cho a, b là những số thực dương. Rút gọn các biểu thức sau :
Chứng minh rằng
z . \2>/5	/ , ýìy/ĩ
a) 4
2 	 ’
ứ3 yfb + b^yjã
^ + Vb
d)
b)
aồ \a J +a:
3
ữ4
+ a 4J
1
1
1 1
a^b
3 .
- a ^b^
c)
a)
Luỹ thừa với số mũ nguyên
\	/	\ 3
Tính (1,5)4 ;	; (V3)5.
Cho n là một số nguyên dương.
Với a là số thực tuỳ ý, luỹ thừa bậc n của a là tích của n thừa số a
Với a * 0
Trong biểu thức am , ta gọi a là cơ số, số nguyên m là số mũ. CHÚ Ý.
0° và 0~” không có nghĩa.
Luỹ thừa với số mũ nguyên có các tính chất tương tự của luỹ thừa với số mũ nguyên dương.
-9
Ví dụ 1. Tính giá trị của biểu thức
A = I .27~3 + (0,2)^.25“2 + 128_1.Q
Giải. A = 310.-1- + —ỉ— . -Ậ- + -4- . 29 =3 + 1 + 4 = 8. 273 0,24 252 128
-3
Ví dụ 2. Rút gọn biểu thức
(ữ 0, a +1).
aự2 2V2
.(1 + đ2)"1
Giải. Với a * 0, a * ±1, ta có
B = [«72(1 + «2) - 272«]- . -	1
«3(1 - a2)
= («72 + «372 - 2«72)——
«3 - a
= a4ĩ(a2 - 1)	= 72.
«(«2 - 1)
Phương trình xn = b
Â2
' ^Dựa vào đồ thị của các hàm số y = x3 và y = x4(H.26, H.27), hãy biện luận theo b
hàm số y = x2k có dạng tương tự đồ thị hàm số y = X4. Từ đó ta có kết
quả biện luận số nghiệm của phương trình xn = b như sau :
Trường hợp n lẻ :
Với moi số thực b, phương trình có nghiệm duy nhất.
Trường hợp n chẵn :
Với b < 0, phương trình vô nghiệm ;
Với b = 0, phương trình có một nghiệm X = 0 ;
Với b > 0, phương trình có hai nghiệm đối nhau.
Căn bậc n
Cho số nguyên dương n, phương trình
an = b
đưa đến hai bài toán ngược nhau :
Biết a, tính b.
Biết b, tính a.
Bài toán thứ nhất là tính luỹ thừa của một số. Bài toán thứ hai dẫn đến khái niệm lấy căn của một số.
Khái niệm
Cho số thực b và số nguyên dương n (zz > 2). Số a được gọi là cãn bậc n của số b nếu an = b.
Chẳng hạn, 2 và -2 là các căn bậc 4 của 16 ; -4 là căn bậc 5 của 4-"
3	243
Từ định nghĩa và kết quả biện luận về số nghiệm của phương trình xn = b , ta có:
Với n lẻ và b e R : Có duy nhất một căn bậc n của b, kí hiệu là yfb.
ỵb < 0 : Không tồn tại căn bậc n của b ;
Với n chẵn vàế-—b = 0 : Có một căn bậc n của b là số 0 ;
> 0 : Có hai căn trái dấu, kí hiệu giá trị dương là y[b , còn giá trị âm là -\/z? .
Tính chất của cãn bậc n
Từ định nghĩa ta có các tính chất sau :
^.^ib=^b ■
\fã - n[ã
y/b - Vồ
n In - la = <
a, khi n lẻ |a|, khi n chẵn ;
'chứng minh tính chất yla.yib = y/ab.
Ví dụ 3. Rút gọn các biểu thức :
a) ^/4.^8;
Giải
líĩ.inĩ = 7-32 = ặ(-2)5 = -2.
^3?3 = ^(Vã)3 =73.
4. Luỹ thừa với số mũ hữu tỉ
b)^373 .
/72
Cho số thực a dương và số hữu tỉ r = —, trong đó m e z,
n g N, n > 2. Luỹ thừa của a với số mũ r là sô' a xác định bởi
m
= <ỉlam
1 3
Ví dụ 4. fii3 = 3/1 = 1 ; 4 2 = 7 ^8j	\8 2
an - y/ã (ứ > 0, n> 2).
1-3
4'J =
Ví dụ 5. Rút gọn biểu thức
5	5
x4y + xy4
(x,y > 0).
Giải. Với X và y là những số dương, theo định nghĩa, ta có r £
Đ =	+	= xy.
+ yĩ
Luỹ thừa với số mũ vô tỉ
ở lớp dưới, ta đã biết số y/ĩ là một số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn :
V2 = 1,414 213 562...
Gọi rn là số hữu tỉ thành lập từ n chữ số đầu tiên dùng để viết V2 ở dạng thập phân, n = 1,2,..., 10.
Sử dụng máy tính, ta tính được 3r,í tương ứng. Ta có bảng ghi các dãy số (rw) và (3r") với n = 1, 2,..., 10 như sau :
n
rn
3r"
1
1
3
2
1,4
4,655 536 722
3
1,41
4,706 965 002
4
1,414
4,727 695 035
5
1,4142
4,728 733 93
6
1,414 21
4,728 785 881
7
1,414 213
4,728 801 466
8
1,414 213 5
4,728 804 064
9
1,414 213 56
4,728 804 376
10
1,414 213 562
4,728 804 386
Người ta chứng minh được rằng khi n -> +00 thì dãy số (3r") dần đến một giới hạn mà ta gọi là 3	.
Sử dụng máy tính bỏ túi (có mười chữ số thập phân), ta có 3^ « 4,728 804 388.
Cho a là một số dương, a là một số vô tỉ. Ta thừa nhận rằng luôn có một dãy số hữu tỉ (r„) có giới hạn là a và dãy số tương ứng (</") có giới hạn không phụ thuộc vào việc chọn dãy số (/•„).
Ta gọi giới hạn của dãy số (àn) là luỹ thừa của a với sô' mũ a, kí hiệu là aa .
aa - lim an với a - lim rn .
/ỉ—»+00
/ỉ—»+co
Chú ý. Từ định nghĩa, ta có ìa = 1 (a e ]R).
II - TÍNH CHẤT CỦA LUỸ THỪA VỚI số MŨ THựC
N Hãy nhắc lại các tính chất của luỹ thừa với sô mũ nguyên dương.
Luỹ thừa với số mũ thực có các tính chất tương tự luỹ thừa với số mũ nguyên dương.
Cho a, b là những số thực dương ; a, /3 là những số thực tuỳ ý. Khi đó, ta có :
= aaP ; (ab)a = aaba;
b) ba ’
Nếu a > 1 thì aa > khi và chỉ khi a > /? . Nếu a khi và chỉ khi a< . Ví dụ 6. Rút gọn biểu thức
E =
(ữ > 0).
Giải. Với 0, ta có
\ỊĨ+1+2-\JĨ
a(y/2-2\y/2+2)
^=a-
(ứ73-i)^+1 Rút gọn biểu thức -■	' r- (a > 0).
ứ^-3.ữ4-V5
Ví dụ 7. Không sử dụng máy tính, hãy so sánh các số 52^ và 53^ Giải. Ta có 2V3 = V12, 3V2 = VĨ8.
Do 12 < 18 nên 2V3 < 3V2.	.
Vì cơ số 5 lớn hơn 1 nên 52^ < 53^.
„,<3^	, <3x3
So sánh các sô 1^-1 và R
Bài tập
Tính :
2 2 a) 95.275;
3	3
b) 1444 : 94;
uỹ thừa
+0,25 2;	d) (0,04)~1,5 - (0,125) 3.
Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng với số mũ hữu tỉ:
_Ị_	£
b) 02. z,3 .6^.
w : ờ6.
Viết các số sau theo thứ tự tăng dần
x-3
b) 98°;(j^	; 325.
a) l3’75; 2- - KHÁI NIỆM
_Ị_
Ta đã biết các hàm số y - xn (rt e N*), y = — = X-1, y - yfx = X2 (x > 0).
X
Bây giờ, ta xét hàm số y = xa với a là số thực cho trước.
II Hàm số y = x“, với a e R, được gọi là hàm số luỹ thừa.
1
 ;
Ha	1	T	/0
Chẳng hạn, các hàm số y = X, y - X, y = y - X3, y = xv , y = X71 X4
là những hàm số luỹ thừa.
 - ìlb2
b)76^ > 73A