SGK Giải Tích 12 - Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Bài đọc thêm: Cung lồi, cung lõm và điểm uốn

GIÁ TRỊ LỚN NHẤT VÀ
GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
I - ĐỊNH NGHĨA
Cho hàm số y =/(x) xác định trên tập D.
Số M được gọi là giá trị lớn nhất của hàm sô' y = /(x) trên
tập D nếu /(%) < M với mọi X thuộc D và tồn tại X'o e D sao
cho /(x0) = M.
Kí hiệu M = max/(x).
D
Số m được gọi là giá trị nhỏ nhất của hàm số y = /(x) trên tập D nếu /(x) > m với mọi X thuộc D và tồn tại Xq e D sao cho /(x0) = m.
Kí hiệu m = min/(x).
D
Ví dụ 1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
- ,1 y = X - 5 + —
X
trên khoảng (0 ; +oo).
Giải. Trên khoảng (0 ; +co), ta có y' = 1 —ụ X2
y' = 0 X2 -1 = 0 X = 1.
Bảng biến thiên
Từ bảng biến thiên ta thấy trên khoảng (0 ; +co) hàm số có giá trị cực tiểu duy nhất, đó cũng là giá trị nhỏ nhất của hàm số.
Vậy min /(x) = -3 (tại X = 1). Không tồn tại giá trị lớn nhất của/(x) (0;+oo)
trên khoảng (0 ; +00).
II - CÁCH TÍNH GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ TRÊN MỘT ĐOẠN
V “Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm sô':
y = X2 trên đoạn [-3 ; 0];
y = ^ịtrên đoạn [3 ; 5]..
Định lí
(	.	77.	7	:>
Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
\	í	:	/
Ta thừa nhận định lí này.
Ví dụ 2. Tính giá trị nhỏ nhất và giá trị lớn nhất của hàm sô' y - sinx
Trên đoạn
Trên đoạn
71 . 6
7Ĩ 7ti 6 ;_6~
Giải
Hình 9
Từ đồ thị cùa hàm số y = sinx (H.9), ta thấy ngay
7rc
6; T
a) Trên đoạn D =
ta có
1
2;y
Từ đó maxy = 1 ;miny =	,
D	D	2
^1 = 1 v2j
7ĩt
b) Trên đoạn E =
6 2”
ta có
1	[ 7t
“2’yl2y
= 15 yƯ2)= -1’=°'
Vậy maxy = 1 ; miny = -1. E	E
Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn
Cho hàm số y -
-X2 +2nếu -2<x< 1 X nếu 1 < X < 3
có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhắt của ham sổ trên đoạn [-2 ; 3] và nêu cách tính.
NHẬN XÉT
Nếu đạo hàm/'(x) giữ nguyên dấu trên đoạn [ứ ; b] thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó,/(x) đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các đầu mút của đoạn.
Nếu chỉ có một số hữu hạn các điểm Xị (Xị < Xj+1) mà tại đó f '(x) bằng 0 hoặc không xác định thì hàm số y - f(x) đơn điệu trên mỗi khoảng(Xị ;Xj+i). Rõ ràng giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn [a ; b] là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút a, b và tại các điểm X. nói trên.
Quy tắc
Tìm các điểm Xị, X2,...,xntrên khoảng (ứ ; ỏ), tại đó/'(x) bằng 0 hoặc f '(x) không xác định.
Tính/(ứ), /Gq), /(x2),/(ố).
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có
M = max f(x), m = min /(%).
[ứ; b]	[a; b]
CHÚ Ý
Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó. Chẳng hạn, hàm số
/(%) - — không có giá trị lớn nhất, giá trị nhỏ nhất trên X
khoảng (0 ; 1). Tuy nhiên, cũng có những hàm số có giá trị lớn nhất hoặc giá trị nhỏ nhất trên một khoảng như trong Ví dụ 3 dưới đây.
Ví dụ 3. Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở bốn góc bốn hình vuông bằng nhau, rồi gập tấm nhôm lại như Hình 11 để được một cái hộp không nắp. Tính cạnh của các hình vuông bị cắt sao cho thể tích của khối hộp là lớn nhất.
Hình 11
Giải. Gọi X là độ dài cạnh của hình vuông bị cắt. Rõ ràng X phải thoả mãn điều kiện 0 < X < -Ệ.
Thể tích của khối hộp là
V(x) = x(a - 2x)2	^0 < X <
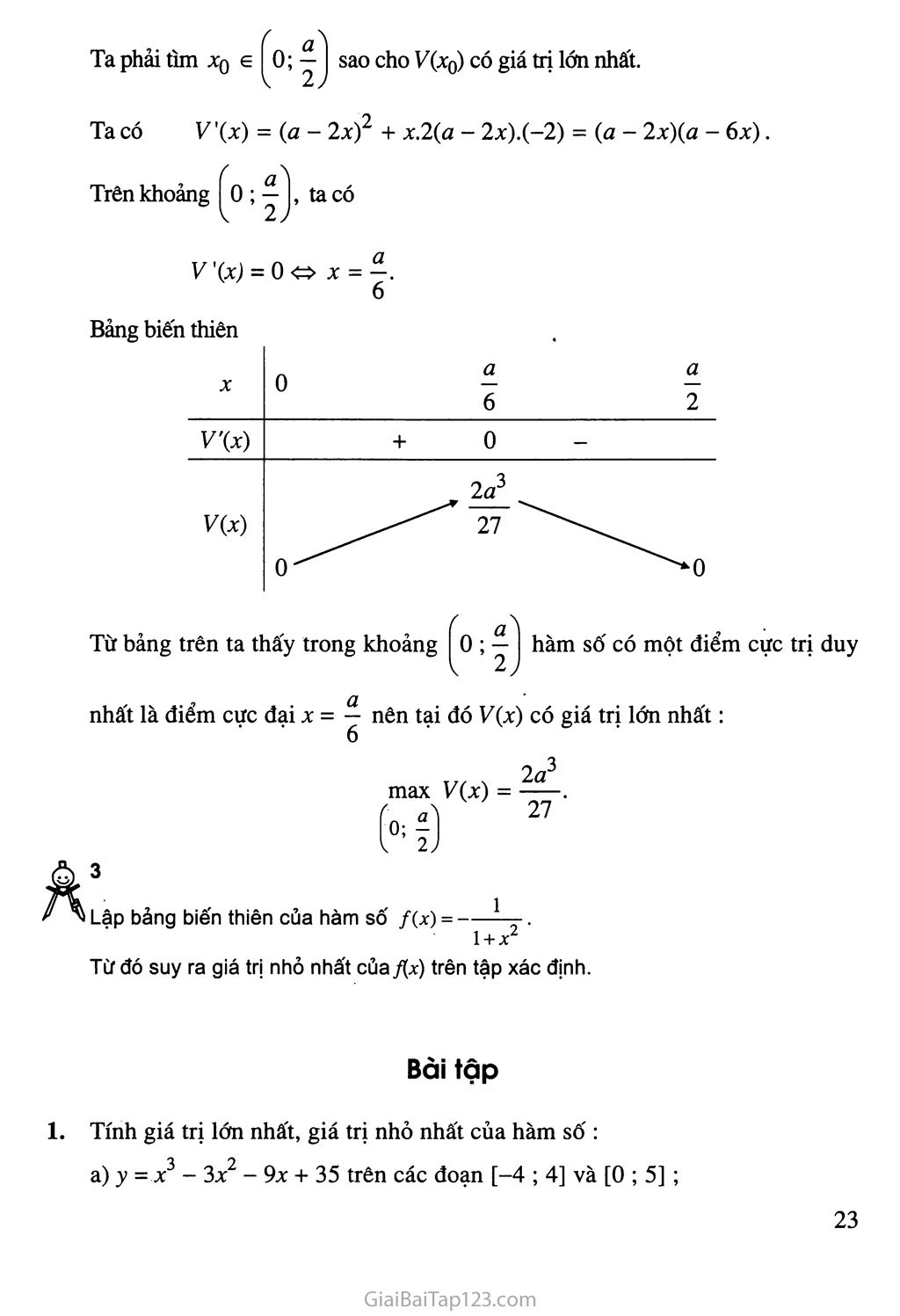
Ta phải tìm Xq e [ o; y J sao cho V(x0) có giá trị lớn nhất.
Ta có V'(x) = (a - 2x)2 + x.2(a - 2x).(-2) = (a - 2x)(a - 6x). Trên khoảng Ị^o ; 1^, ta có
V(x) = o X = ị.
Bảng biến thiên
nhất là điểm cực đại X = nên tại đó V(x) có giá trị lớn nhất: 6
max V(x) =
Lập bảng biến thiên của hàm số /« =	
1 + x2
Từ đó suy ra giá trị nhỏ nhất của/(*) trên tập xác định.
Bài tạp
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số :
y = X3 - 3x2 - 9x + 35 trên các đoạn [-4 ; 4] và [0 ; 5] ;
y = X4 - 3x2 + 2 trên các đoạn [0 ; 3] và [2 ; 5] ;
2 — X
y = 7—-trên các đoạn [2 ; 4] và [-3 ; -2] ;
1 - X
y = ự5 - 4xtrên đoạn [-1 ; 1],
Trong số các hình chữ nhật cùng có chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Trong tất cả các hình chữ nhật cùng có diện tích 48 m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Tính giá trị lớn nhất của các hàm số sau :
a) y =	4	;	b) y = 4x3 - 3x4.
+ x2
Tính giá trị nhỏ nhất của các hàm số sau :
,,	4
a) y = IXI ;	b) y = X + — (x > 0).
X
BÀI Đ
ỌC THÊM
CUNG LÓI, CUNG LÕM VÀ ĐlỂM uốn
1. Khái niệm về cung lồi, cung lõm và điểm uốn
Xét đổ thị ACB của hàm sô' y = f(x) biểu diễn trên Hình 12. Giả sử đồ thị có tiếp tuyến tại mọi điểm.
Tại mọi điểm của cung AC , tiếp tuyến luôn luôn ở phía trên của AC . Ta
nói AC là một cung lồi. Nếu a là hoành độ của điểm A, c là hoành độ của điểm c, thì khoảng (ứ; c) được gọi là một khoảng lồi của đồ thị.
Tại mọi điểm của cungCB, tiếp tuyến luôn luôn ở phía dưới củaCS .
Ta nói CB là một cung lõm. Kí hiệu b là hoành độ của điểm B thì khoảng (c; b) được gọi là một khoảng lõm của đồ thị.
Điểm phân cách giữa cung lồi và cung lõm được gọi là điểm uốn của đồ thị. Trên Hình 12, c là một điểm uốn.
CHÚ Ý
Tại điểm uốn, tiếp tuyến đi xuyên qua đồ thị (H.12).
Trong một sô' giáo trình, nhất là giáo trình Giải tích toán học ở Đại học, người ta gọi AC trên Hình 12 là cung lõm và CB là cung lồi.
í
Dấu hiệu lồị, lõm và điểm uốn
Ta có hai định lí sau đây.
ĐỊNH LÍ 1
X
—00	0	+00
y"
0 +
Đồ thị của hàm số
Vậy đồ thị hàm trên khoảng (0 ; của đồ thị hàm
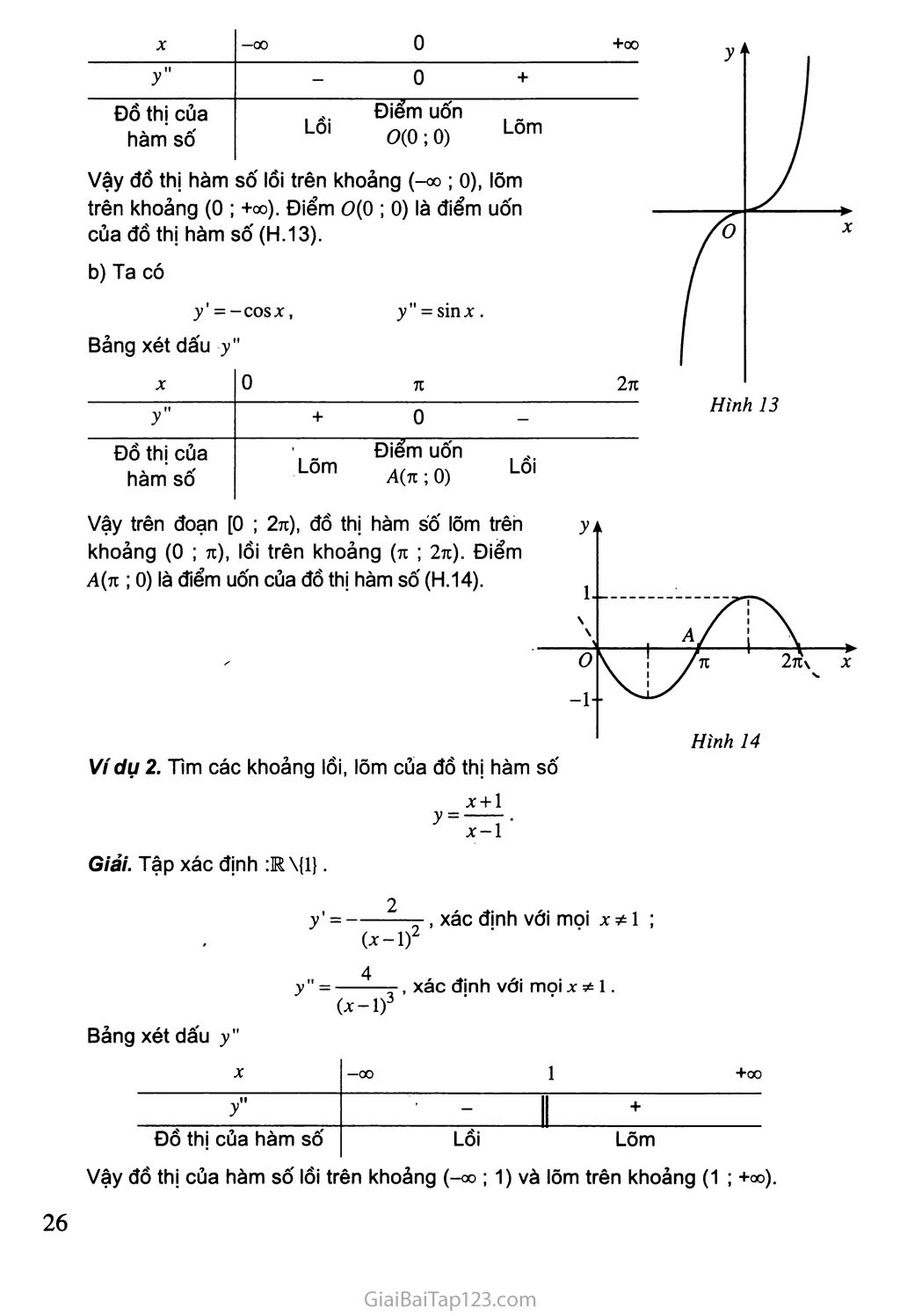
b) Ta có
/ = -
Bảng xét dấu y
X
Điểm uốn
Lố	ơ(0; 0)	Lõm
sô' lồi trên khoảng (-00; 0), lõm +00). Điểm ỡ(0 ; 0) là điểm uốn
5Ố (H.13).
-cosx,	y" = sinx.
1
0	7C	2%
y"
+ 0 -
Đồ thị của hàm sô'
Điểm uốn
Lõm	Â(n; 0)	Lồi
Hình 13
*1
Vậy trên đoạn [0 ; 2tc), đồ thị hàm số lõm trên khoảng (0 ; 7i), lồi trên khoảng (71 ; 2n). Điểm A(n ; 0) là điểm uốn của đồ thị hàm số (H.14).
Ví dụ 2. Tìm các khoảng lồi, lõm của đồ thị hàm sô' x + 1
x-ỉ
Giải. Tập xác định :R \{1}.
y' =	——, xác định với mọi X * 1 ;
u-l)2
Bảng xét dấu y"
y" = ———, xác định với mọi X * 1. (x-1)3
X
—00	1	+00
y”
-
+
Đồ thị của hàm sô'
Lồi	Lõm
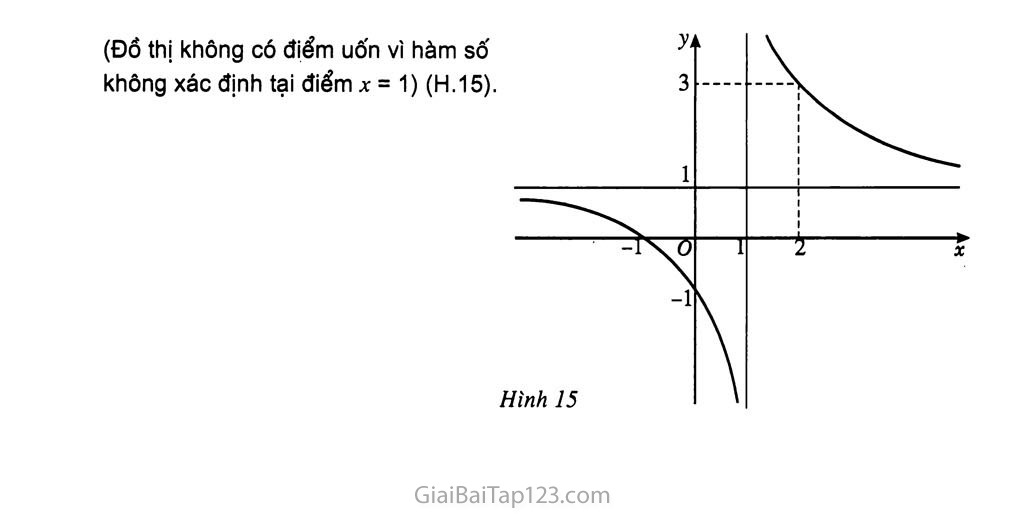
Vậy đồ thị của hàm số lồi trên khoảng (-00 ; 1) và lõm trên khoảng (1 ; +00).
(Đồ thị không có điểm uốn vì hàm số không xác định tại điểm X = 1) (H.15).