SGK Giải Tích 12 - Bài 3. Lôgarit - Bạn có biết: Ai đã phát minh ra lôgarit

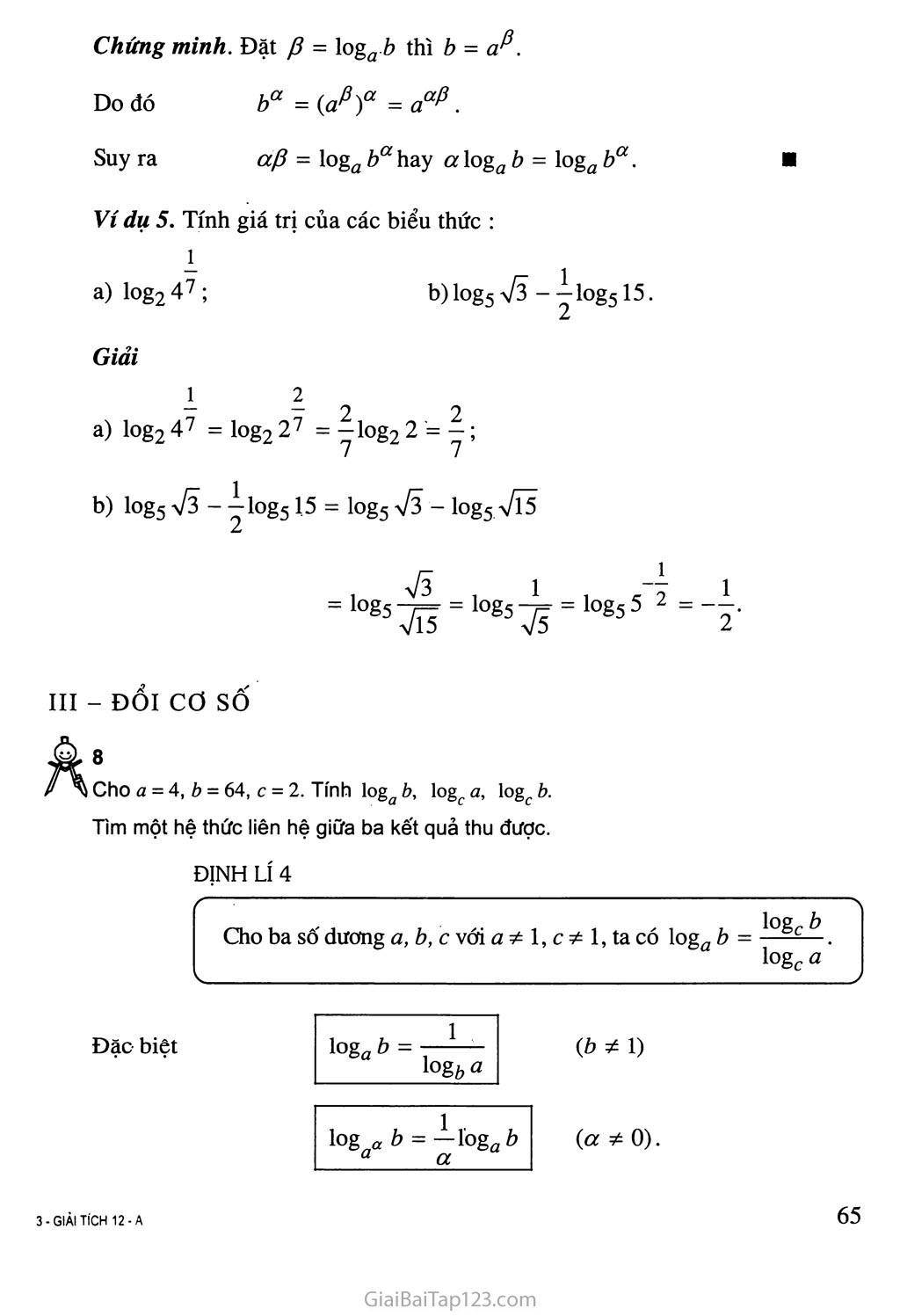
LÔGARIT
Bài toán thứ nhất là tính luỹ thừa với số mũ thực của một số. Bài toán thứ hai dẫn đến khái niệm lấy lôgarit của một số. Người ta chứng minh được rằng với hai số dương a, b, a 1, luôn tồn tại duy nhất số a sao cho aa - b.
Định nghĩa
Cho hai số dương a, b với a 1. Số a thoả mãn đẳng thức aữ = b được gọi là lôgarit cơ số a của b và kí hiệu là logữ b. a = logứ b aa - b.
Vídụl
a) log2 8 = 3
vì 23 = 8 ;	b) log! 9 = -2 vì = 9.
3
a) Tính log j 4,
logo
3 27
b) Có các số X, y nào để 3* =0, 2y = -3 hay không ?
CHÚ Ý
Không có lôgarit của số âm và số 0.
Tính chất
Cho hai số dương avab, at 1. Ta có các tính chất sau đây.
logứ 1 = 0, logữ a = 1,
Qlogafr = bí Ioga(flg) = a,-
3
Hãy chứng' minh các tính chất trên.
Ví dụ 2
321og35 = (3log3 5)2 = 52 = 25
log^ 8 = log^ = -3.
2 2 v
Tính 4
- QUY TẮC TÍNH LÔGARIT
5
Cho^=23, ò2=25.
Tính log2 bị + log2 b2 ; log2(.òjò2) và so sánh các kết quả.
Lôgarit của một tích
ĐỊNH LÍ 1
Cho ba số dương a, bỵ, z?2 với a * 1, ta có
Ịọgạ (^2 ) = Ịọgạ + Iog« b2 • z
Lôgarit của một tích bằng tổng các lôgarit.
Chứng minh. Đặt ƠỊ = logứ bỵ, a2 - logứ h2’ ta có
Ví dụ 3. Tính log6 9 + log6 4
Giải. log6 9 + log6 4 = log6(9.4) = log6 36 = 2.
CHÚ Ý
Định lí 1 có thể mở rộng cho tích của 72 số dương : l°ga(W-A) = log« bỵ + logữ b2 + ... + logữ bn
(ứ, bị, b2,bn>ữ,a* 1).
sẻ 6
1	3
Tính log! 2 + 21ogj l + log, j.
2 2 2
Lôgarit của một thương 7
Cho bị = 25, b2 = 23. Tính log2 bị -log2 b2, log2 và so sánh các kết quả.
b2
ĐỊNH LÍ 2
Cho ba số dươnga, bỵ, t>2 với a * 1, ta có bỵ
ỉ°êaT- = ỉ°êabỉ ~ỉoêab2-
Đặc biệt
Lôgarỉt của một thương bằng hiệu các lôgarit.
logứỊ = -k>ẽab
(ứ > 0, b > 0, a * 1).
Định lí 2 được chứng minh tương tự Định lí 1.
Ví dụ 4. Tính log7 49 - log7 343.
49	.	1
Giải.	log7 49 - log7 343 = log7 = log7 y = -log7 7 = -1.
Lôgarit của một luỹ thừa
ĐỊNH LÍ 3
Cho hai số dương a,b;a*ỉ. Với mọi a, ta có ỉogaba = aỉogữb.
	.	X
Lôgarit của một luỹ thừa bằng tích của sô' mũ với lôgarit của cơ số.
Đặc biệt
loga^ = 7logứố. n
Chứng minh. Đặt p = logứ b thì b =	.
Do đó	ba - (a@)a = aap .
Suy ra	a/3 - logữ z?ưhay «logứ b = logữ ba.	■
Ví dụ 5. Tính giá trị của các biểu thức :
log247;	b)log5 73 - |log515.
Giải
1 2
log2 47 = log2 27 = |log2 2 = I;
log5 73 - 2 v b = “Ioỗ« b
a a
ể5 15 = log5 73 - log5 7Ĩ5
= 1°Ỗ5
7s
7B
log57?
log55
- ĐỔI Cơ SỐ
Cho a = 4, b = 64, c = 2. Tính loga b, log£. a, logc b. Tìm một hệ thức liên hệ giữa ba kết quả thu được.
ĐỊNH LÍ 4
Cho ba số dương a, b, c với a 1, c * 1, ta có log,. b = l£ẵcA.
logc a
Đặc biệt
	y
(ồ*l)
(<z * 0).
l°gữ b = 7-7— logfr
Chứng minh. Theo tính chất của lôgarit và Định lí 3, ta có logc b = logc(«log^) = logữ h.logc a.
Vì a 1 nên logc a * 0. Do đó
logứ b =
 logcfr
logcữ
- VÍ DỤ ÁP DỤNG
Ví dụ 6. Tính :
logj_2
a)2log415;	b)3	27 .
Giải
Ta có log415 = log 2 15 = 7-log2 15 = log2 Vl5 .
2 2
Do đó 2Iog415 = 2log2 = 7Ĩ5 .
1 „-1 , 1
Vì logj_ 2 = log 3 2 = “log3 2 = log3 2 3 = log3 —
27	3	3	V2
logj_2 log3^= nện 3	27	= 3 v2 t
Ví dụ 7. Cho a = log2 20. Hãy tính log20 5 theo a.
Giải. Ta có
a = log2 20 = log2(22.5) = 21og2 2 + log2 5 = 2 + log2 5, suy ra	log2 5 = a — 2.
log205 =
log2 5 log2 20
Ví dụ 8. Rút gọn biểu thức
A = log± 7 + 21ogọ 49 - logự^ ệ.
Giải. Ta có
A = log 1 7 + 2 log 2(72) - log ị(7_1)
J	32
= - log3 7 + 21og3 7 + 21og3 7 = 31og3 7 . Ví dụ 9. So sánh các số log2 3 và log6 5 .
Giải. Đặt a = log2 3 , p = log6 5.
Ta có 2a - 3 > 21nên a > 1 ; 6^ = 5 p.
Vậy log2 3 > log6 5.
- LÔGARIT THẬP PHÂN. LÔGARIT TựNHIÊN
Lôgarit thập phân
Lôgarit thập phân là lôgarit cơ sô' 10. logỊQồ thường được viết là logố hoặc lgố.
\n
có giới hạn là
Lôgarit tự nhiên
Người ta chứng minh được dãy sô' (wrt)với un = một sô' vô tỉ và gọi giới hạn đó là e,
e=ltafl + iT. ■ rt-»+oo^ n J
Một giá trị gần đúng của e là e « 2,718 281 828 459 045.
Lôgarit tự nhiên là lôgarit cơ số e. loge b được viết là lnờ.
CHÚ Ý
Muốn tínhlogữZ?, với ứ * 10 vàữ e, bằng máy tính bỏ túi, ta có thể sử dụng công thức đổi cơ số.
Chẳng hạn,
log2 3 = 7^4 « í’584 962 501.
log30,8 =
log 2 ln 0,8
In 3
-0,203 114 013.
Bài tập
b) log! 2; 4
Không sử dụng máy tính, hãy tính : a) log2|;
d) log0í5 0,125.
b) 27log92; d) 4log827.
log3 3/3 ;
Tính : a) 4log23;
9l0g^2;
b) logữ b + logứ2 b .
Rút gọn biểu thức : a) log3 6. logg 9. logg 2 ;
So sánh các cặp số sau :
log35và log74 ;
log0í3 2 và log5 3 ;
log210và log530.
Cho a = log30 3, b = log3Q 5. Hãy tính log3Q 1350 theo a, b.
Cho c = log15 3. Hãy tính log2515 theo c.
BAN CÓ BIẾT
AI ĐÃ PHÁT MINH RA LÔGARIT ?
Nê-pe (John Napier) là nhà toán học Xcốt-len (Scotland).
Ông sinh năm 1550 tại Me-ti-ston (Metiston-Castle), gần thành phô' Ê-đin-bơc (Edinburgh) và tốt nghiệp trường Đại học Tổng hợp Ê-đin-bơc.
Nê-pe là người phát minh ra lôgarit. Thuật ngữ "Lôgarit" do ông đề nghị xuất phát từ sự kết hợp hai từ Hi Lạp À.ÓỴOC; (đọc là "logos" có nghĩa là tỉ số) và 'apiOp ót; (đọc là "aritmos" có nghĩa là số). Trong toán học cổ, bình phương, lập phương,... được gọi là các tỉ sô' kép, bội ba,... Như vậy, đối vối Nê-pe, từ
À.ÓỴOS 'api Opós có nghĩa là "số tỉ số". Lôgarit được Nê-pe	J. Napier
xem là số trợ giúp để tính tỉ số của hai số.	(1550 - 1617)
Trong tác phẩm "Mô tả bảng lôgarit kì diêu" (1614), Nê-pe đưa ra định nghĩa và
các tính chất của lôgarit. Lôgarit mà Nê-pe xét có cơ số gần bằng - .
e
Thuật ngữ "Lôgarit tự nhiên" do Men-gô-li (P. Mengoli - 1659) và Men-ca-tơ (N. Mencator - 1668) đưa ra. Năm 1893, Prin-xêm (A. Pringshelm) đã kí hiệu lôgarit tự nhiên của số N bởi In N. Bởi vậy, việc gọi lôgarit tự nhiên là lôgarit Nê- pe không có cơ sở. Tuy nhiên, người ta vẫn thường gọi như vậy có lẽ là do đã gắn lôgarit tự nhiên với tên người thiết lập bảng lôgarit đầu tiên.
Ngoài ra, Nê-pe còn là tác giả của một loạt các công thức dành cho việc giải các tam giác cầu, rất tiện lợi cho việc lấy lôgarit.
Ngày 4-4-1617, Nê-pe qua đời tại quê hương ông.