SGK Giải Tích 12 - Bài 4. Hàm số mũ - Hàm số Lôgarit

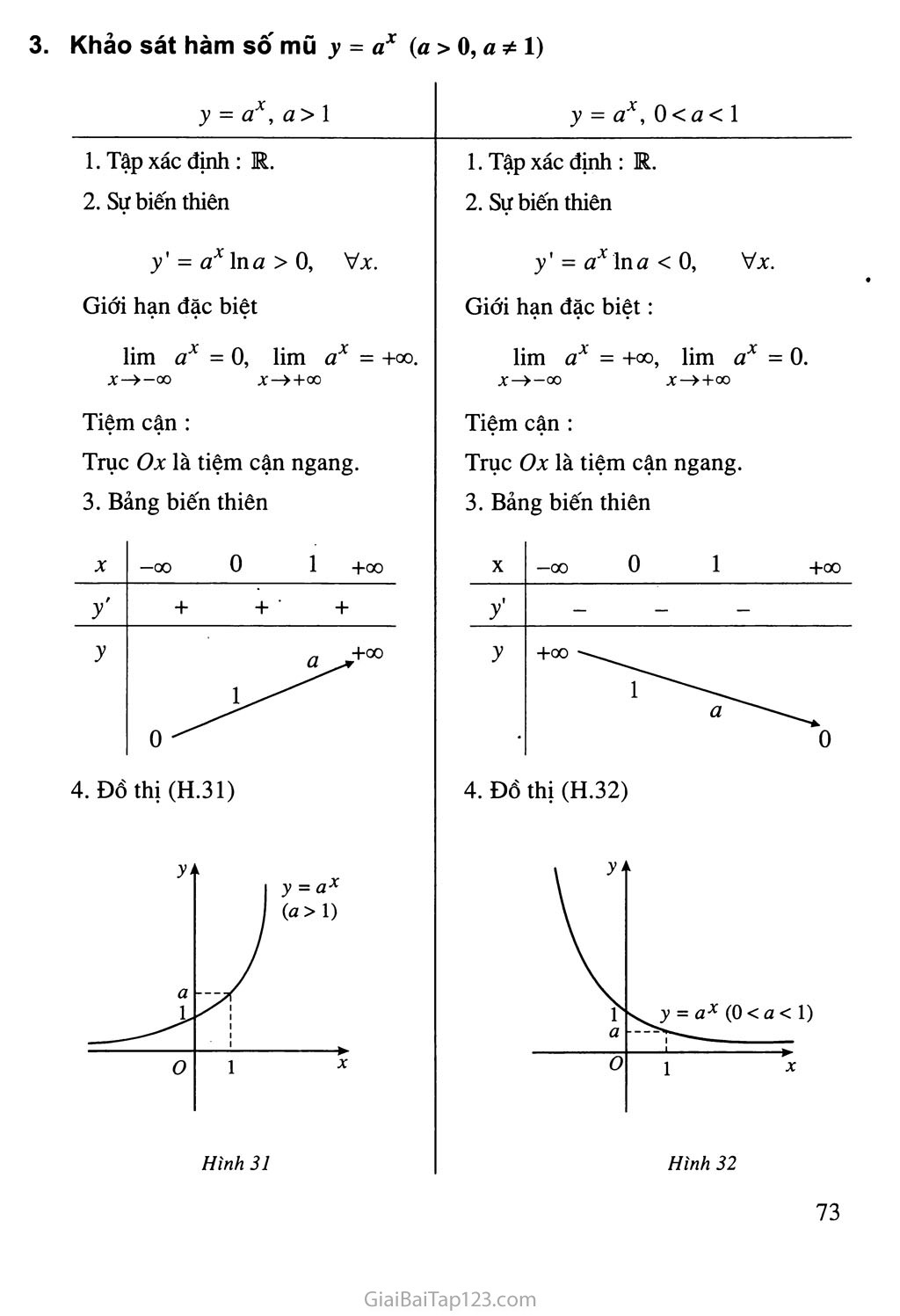
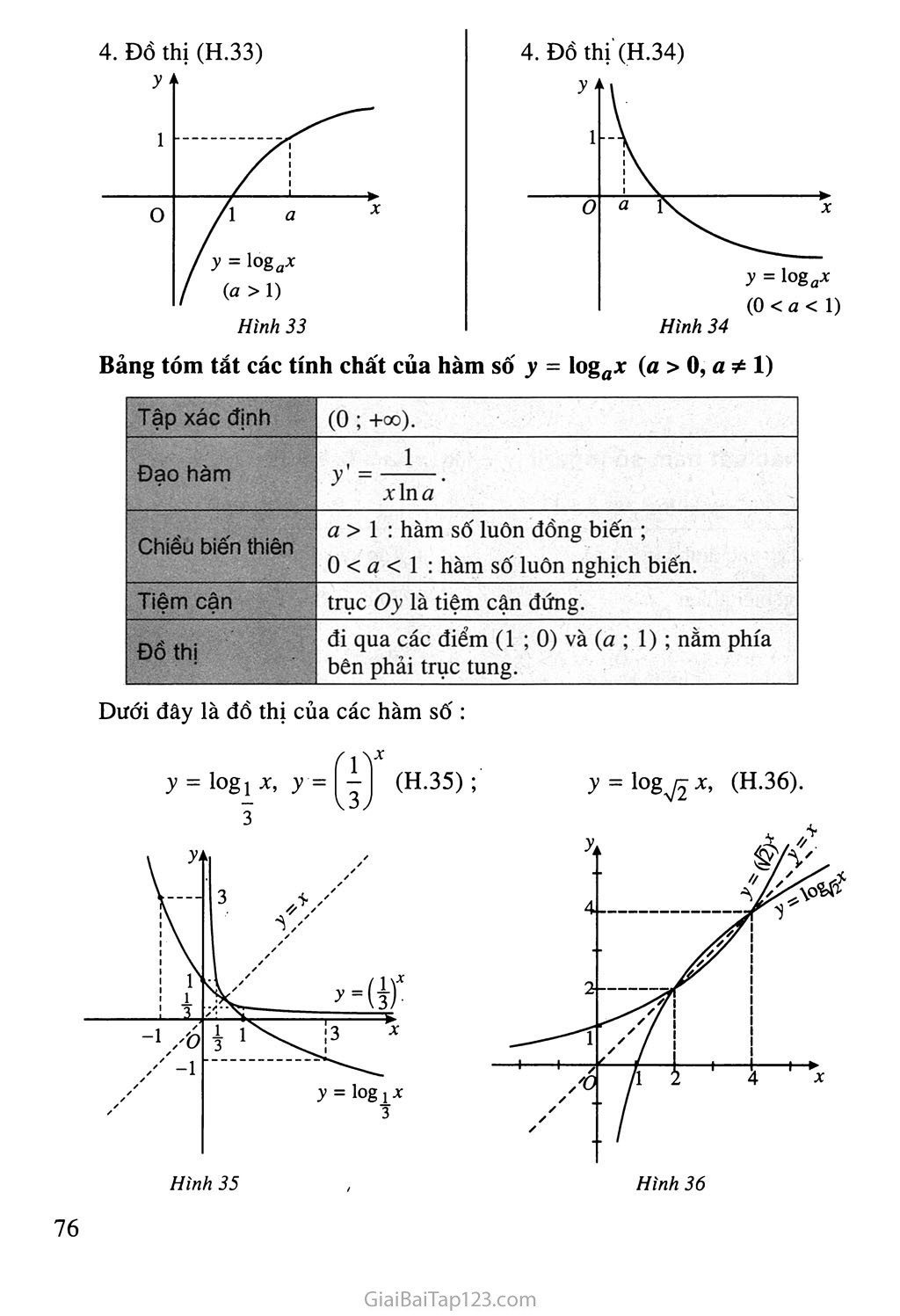
HÀM SỐ MŨ. HÀM SỐ LỒGARIT
I - HÀM SỐ MŨ
'Vi dụ 1. Bài toán "lãi kép"
Một người gửi số tiền 1 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Hỏi người đó được lĩnh bao nhiêu tiền sau n năm (« e N*), nếu trong khoảng thời gian này không rút tiền ra và lãi suất không thay đổi ?
Giải. Giả sử n > 2. Gọi số vốn ban đầu là p, lãi suất là r. Ta có p = 1 (triệu đồng), r• = 0,07.
• Sau năm thứ nhất:
Tiền lãi là ?! = Pr = 1.0,07 = 0,07 (triệu đồng).
Số tiền được lĩnh (còn gọi là vốn tích luỹ) là
Pị = p + Tị = p + Pr = P(i + r) = 1,07 (triệu đồng).
• Sau năm thứ hai:
Tiền lãi là T2 = Pự = 1,07.0,07 = 0,0749 (triệu đồng). Vốn tích luỹ là P2 = Pl+T2=Pỉ + PỴr = ?i(l + r)
= P(1 + r)2 = (l,07)2 = 1,1449(triệu đồng). • Tương tự, vốn tích luỹ sau n năm là
Pn = P(1 + r)n = (1,07)" (triệu đồng).
Vậy sau n năm, người đó được lĩnh (1,07)" triệu đồng.
Ví dụ 2. Trong Vật lí, sự phân rã của các chất phóng xạ được biểu diễn bằng công thức
m(t) = mQ	,
trong đó ỈĨĨQ là khối lượng chất phóng xạ ban đầu (tại thời điểm t = 0), m(í)
là khối lượng chất phóng xạ tại thời điểm t, T là chu kì bán rã (tức là khoảng thời gian để một nửa số nguyên tử của chất phóng xạ bị biến thành chất khác).
Ví dụ 3. Dân số thế giới được ước tính theo công thứcS = Aem, trong đó A là dân số của năm lấy làm mốc tính, 5 là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm.
Cho biết năm 2003, Việt Nam có 80 902 400 người và tỉ lệ tăng dân số là 1,47%. Hỏi năm,2010 Việt Nam sẽ có bao nhiêu người, nếu tỉ lệ tăng dân số hàng năm không đổi ?
Những bài toán thực tế như trên đưa đến việc xét các hàm số có dạng y = ax.
* 1. Định nghĩa
Cho số thực dương a khác 1.
Hàm số y = ax được gọi là hàm số mũ cơ số a.
2
Trong các hàm sô' sau đây, hàm số nào là hàm sô' mũ ? Với cơ sô' bao nhiêu ? a)y = (V3)x;	b)y = 53;	c)y = x^;	d) y = 4~x.
Đạo hàm của hàm số mũ
Ta thừa nhận công thức
lim——— = 1.	(1)
t^>0 t
ĐỊNH LÍ 1
	-	
Hàm số y = ex có đạo hàm tại mọi X và
,(exy = ex-
Chứng minh. Giả sử Ax là số gia của X, ta có
Ay = ex+^ -ex =^(^-1).
Do đó
Ay .A^-l Ar	Ax
Áp dụng (1), ta có
eAv - 1
lim —-—- = 1.
Ax—»0 Ax
Từ đó suy ra
y'= lim ^- = ex.	■
Ax-»OÁX
CHÚ Ý
Công thức đạo hàm của hàm hợp đối với hàm số elt (w = w(%)) là (e“).' = u'.eu.
ĐỊNH Ú 2
?	X	?	?	■>
Hàm số y ;= ax (a > 0, a 1) có đạo hàm tại mọi X và (axy = ax ln<2 .
	 7 	/
Chứng minh. Ta có
X	lnứA _ „xlnơ
a = e = e .
Đặt u(x) = xin ứ, theo Chú ý trên, ta được
(axy = (exỉnay = exỉna(xỉnay = axìna. ■
CHÚ Ý
Đối với hàm hợp y = au(x\ ta có
(auy = ơlílna ■ li'.
Ví dụ 4. Hàm số y = 8A~ +A + 1 có đạo hàm là
/ = 8A'2+A+1(x2 + X + l)Tn8 = 8A'2+A+1(2x + l)ln8.
3. Khảo sát hàm số mũ y = ax (a > 0, a * 1)
y = ax, a > 1
y = ax, 0 < a < 1
Tập xác định : R.
Sự biến thiên
Tập xác định :
Sự biến thiên
R.
/ =
ax In a > 0, Vx.
y' = ax In a < 0,	Vx.
Giới hạn đặc biệt
Giới hạn đặc biệt:
lim a*
X—>-00
= 0, lim ax = +00.
X—>+00
lim ax = +GO, lim ax = 0.
X->-00	X—> + 00
Tiệm cận :
Trục Ox là tiệm cận ngang.
3. Bảng biến thiên
Tiệm cận :
Trục Ox là tiệm cận ngang.
3. Bảng biến thiên
X
—00
0 1 +00
X
—00
0 1 +00
y'
+
+ ■ +
y'
—
— —
y
0
ứ^+ũ0
y
+00
0
4. ĐỒ thị (H.31)
4. Đồ thị (H.32)
y‘
1 y = ax / («>1)
\ y'
Ị
a
L
s' 1 ' 1
1
1
1 .
r
a
\y = ax (0 < a < V)
0
	►
1 x
o
	1	>.
1	X
Hình 31
Hình 32
Bảng tóm tắt các tính chất của hàm sô mũ y = ax (a > 0, a 1)
Tập xác định
(-00 ; +oo).
Đạo hàm
y' = aỵ lnư.
Chiều biến thiên
ứ > 1 : hàm số luôn đồng biến ;
0 < a < 1 : hàm số luôn nghịch biến.
Tiệm cận
trục Ox là tiệm cận ngang.
Đổ thị
đi qua các điểm (0 ; 1) và (1 ; ứ), nằm phía trên trục hoành
(y = ax > 0, Vx e R).
II - HÀM SỐ LÔGARIT
Định nghĩa
Cho số thực dương a khác 1.
Hàm số y = logứ X được gọi là hàm số lôgarit cơ số a.
Ví dụ 5. Các hàm số y = Iog3 X, y = log! X, y = log 7? X, y = ỉnx, y = logX 4
là những hàm số lôgarit với cơ số lần lượt là 3, -ị, 75, e và 10.
4
Đạo hàm của hàm số lôgarit
Ta có định lí sau đây.
ĐỊNH LÍ 3
Hàm số y = logữ X (ứ > 0, 0 và
(logứ xỴ = -7—•
\_	7
Đặc biệt
CHU Y .
Đối với hàm hợp y = loga i/(x), ta có
(logữ uỴ =
win <2
Ví dụ 6. Hàm số y = log2(2x + 1) có đạo hàm là
I _	nv _	+ 1)'	2
2	(2x + l)ln2 (2x + l)ln2
1 Tìm đạo hàm của hàm số J = ln(x + Vl + X2).
3. Khảo sát hàm số lôgarit y = logflx (« >o,fl^ 1)
y = logữ X, a > 1
y = logữ X, 0 < a < 1
1. Tập xác định : (0 ; +oo).
1. Tập xác định : (0 ; +oo).
2. Sự biến thiên
2. Sự biến thiên
y' = —-—- >0, Vx > 0. xlna
y'=	1	 0.
xlna
Giới hạn đặc biệt:
Giới hạn đặc biệt:
lim log „ X - -00,
X-+Õ+
lim logữ X = +00,
X—>0+
lim logữ X - +00.
X-++00
lim logữ X = -00.
X—» + oo
Tiệm cận :
Tiệm
cận :
Trục Oy là tiệm cận đứng.
Trục Oy là tiệm cận đứng.
3. Bảng biến thiên
3. Bảng biến thiên
X
0	1	a +00
X
0	a	1	+00
y'
+ + +
y'
_ _ _
y
■	_^>r+0O
y
+00-^1
—00 0
—00
Bảng tóm tắt các tính chất của hàm sô y = ỉogax (a > 0, a 1)
Tập xác định
(0 ; +00).
Đạo hàm
T -	1	■
xin ứ
Chiểu biến thiên
a > 1 : hàm số luôn đồng biến ;
0 < a < 1 : hàm số luôn nghịch biến.
Tiệm cận
trục Oy là tiệm cận đứng.
Đồ thị
đi qua các điểm (1 ; 0) và (ứ ; 1); nằm phía bên phải trục tung.
Dưới đây là đồ thị của các hàm số :
Nêu nhận xét về mối liên hệ giữa đồ thị của các hàm sô' trên Hình 35 và Hình 36. NHẬN XÉT
Đồ thị của các hàm số y = ầ và y - loga X (ữ > 0, a * 1) đối xứng với nhau qua đường thẳng y = X.
Bảng đạo hàm của các hàm số luỹ thừa, mũ, lôgarit
Hàm sơ cấp
Hàm hợp (« = «(x»
(xay = axa-ỵ
(«“)' = aua~ỵ.u'
m' 1
A'=-4
vxj	X2
u	M2
GO' = *
2Vx
(7^)' =
27m
(ex)’ = ex
(e“)' = euu'
(ưx) ’ = ax In a
(ứ“)' = au An a.u'
(ln|x|)’ = - X
(ln |w|)' = — u
(logjxl)’- 1
X In ơ
(log>|)'-
Min a
Bài tập
a)y = 4X ;
Vẽ đồ thị của các hàm số :
X + 1
3X
Tính đạo hàm của các hàm số :
y = 2xex + 3sin2x ; b)y - 5x2 - 2X cosx ;	c)y
Tìm tập xác định của các hàm Số :
à) y = log2(5 - 2x);	b) y = log3(x2 - 2x);
c) y = logjCx2 -4x + 3);	d)y = logo4 3* + 2 •
.	1 - X
Vẽ đồ thị của các hàm số : a)y = log X;
X
Tính đạo hàm của các hàm số : 2
a)y - 3x -lnx + 4sinx;