SGK Giải Tích 12 - Bài 2. Hàm số lũy thừa

HÀM SỐ LUỸ THỪA
1
Vẽ trên cùng một hệ trục toạ độ đồ thị của các hàm số sau và nêu nhận xét về tập
£
xác định của chúng : y = x\ y = x2,y = x~ì.
CHÚ Ý
Tập xác định của hàm số luỹ thừa y - xa tuỳ thuộc vào giá trị của a. Cụ thể,
Với a nguyên dương, tập xác định làR ;
Với a nguyên âm hoặc bằng 0, tập xác định làR \ {0}; Với a không nguyên, tập xác định là (0 ; +oo).
II - ĐẠO HÀM CỦA HÀM số LUỸ THỪA
Ở lớp 11, ta đã biết đạo hàm của các hàm số y = xn (n eỉỊn>i) và y = 4x là
(xnỵ = nxn~Ỵ (xgR);
(Vx)' = —hay Q2
Một cách tổng quát, người ta chứng minh được hàm số luỹ thừa y = xa (« e R) có đạo hàm với mọi X > 0 và
(/)' = axa~Ỵ.
Vídụl
3
a) U-4J =-x, 4 =
(% > 0);
b) (x^) = V3x^_1(%>0).
Tính đạo hàm của các hàm số :
CHƯ Y
Công thức tính đạo hàm của hàm hợp đối với hàm số luỹ thừa có dạng
(uay = aua~ỉ.u'.
Ví dụ 2
lì' 2	-lo
(2x2 + X - 1)3 ) = |(2x2 + X - 1) 3(2x2 + X - 1)'
2(4x + 1)
3^2x2 + X - 1
à 3
Tính đạo hàm của hàm so y = (3x -1)	.
III - KHẢO SÁT HÀM SỐ LUỸ THỪA y = xa
Tập xác định của hàm số luỹ thừa y - xa luôn chứa khoảng (0 ; +oo) với
mọi a e R. Trong trường hợp tổng quát, ta khảo sát hàm số y = xa trên khoảng này (gọi là tập khảo sát).
y = xa, a > 0
y = xa, a < 0
Tập khảo sát: (0 ; +00).
Sự biến thiên
Tập khảo sát: (0; +oo).
Sự biến thiên
y' =	> 0, Vx>0.
y' =	0.
Giới hạn đặc biệt:
Giới hạn đặc biệt:
lim xa = 0, lim xa = +00.
X—>0+	x^+co
lim xa - +OO, lim xa = 0. x->0+	X—>+00
Tiệm cận : Không có.
Tiệm cận :
Trục ơx là tiệm cận ngang,
Trục Oy là tiệm cận đứng của đồ thị.
4. Đồ thị (H. 28 với a > 0).
X
0 +00
y'
-
y
+00 	
3. Bảng biến thiên
4. Đồ thị (H. 28 với a < 0).
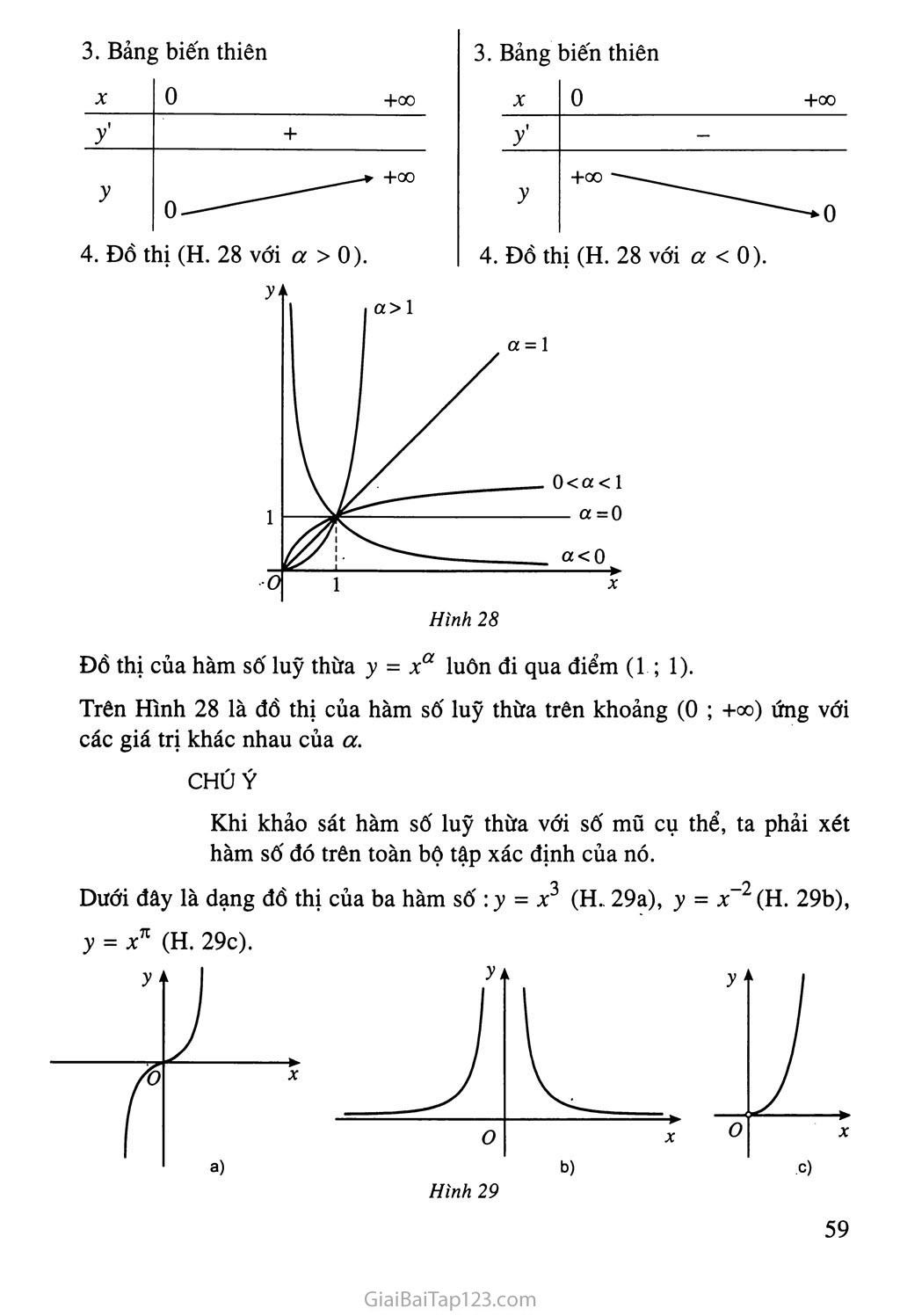
Đồ thị của hàm số luỹ thừa y = xa luôn đi qua điểm (1 ; 1).
Trên Hình 28 là đồ thị của hàm số luỹ thừa trên khoảng (0 ; +00) ứng với các giá trị khác nhau của a.
CHÚ Ý
Khi khảo sát hàm số luỹ thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
Dưới đây là dạng đồ thị của ba hàm số : y = X3 (H.. 29a), y = x~2 (H. 29b),
_ 3
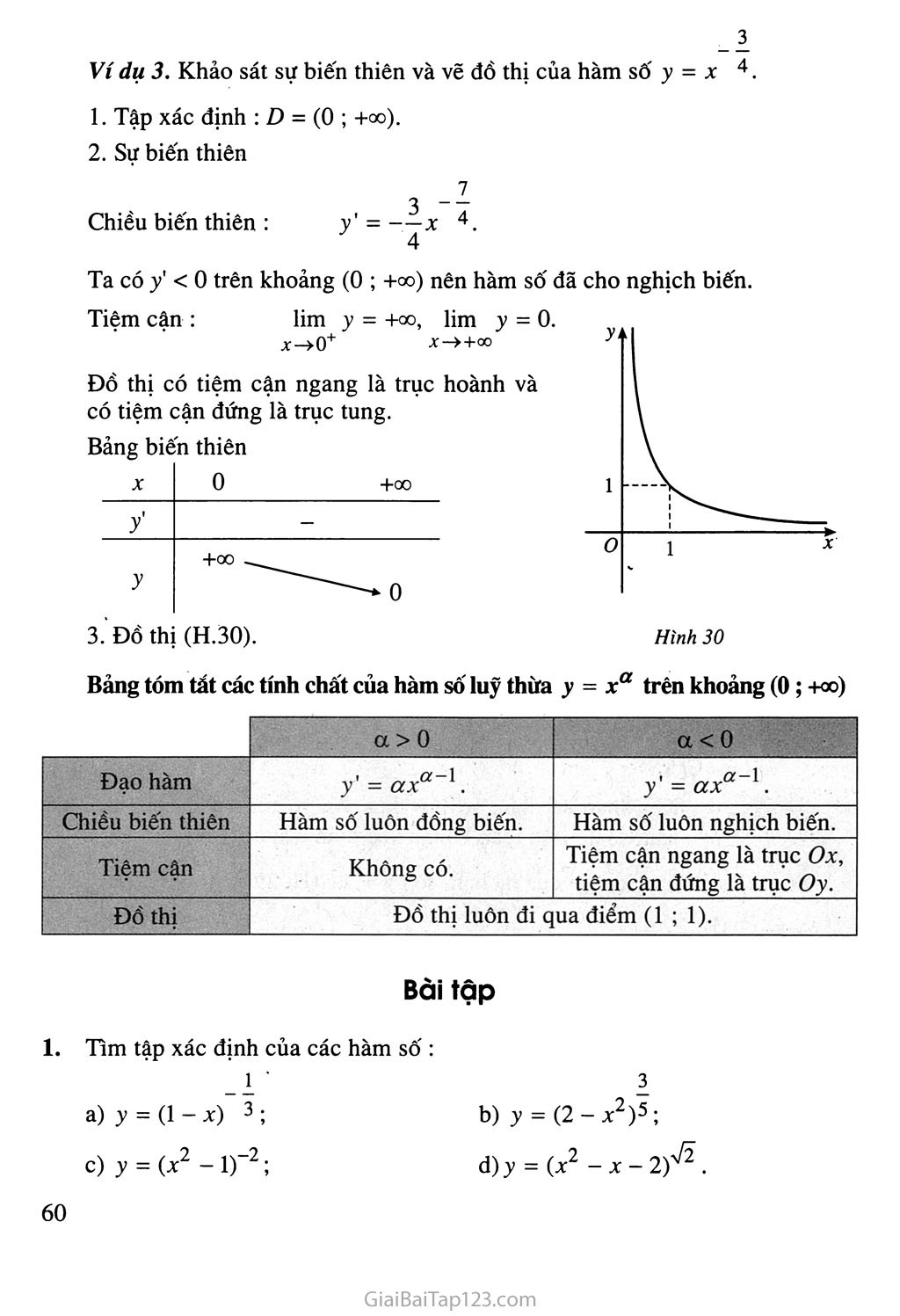
Ví dụ 3. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = X 4.
Tập xác định : D = (0 ; +oo).
Sự biến thiên
Chiều biến thiên :
Ta có y' < 0 trên khoảng (0 ; +00) nên hàm số đã cho nghịch biến.
Hình 30
Tiệm cận :	lim y = +00, lim y = 0.
x->0+	x-»+00
Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.
+00
Bảng biến thiên
+00
Đồ thị (H.30).
Bảng tóm tắt các tính chất của hàm sô luỹ thừa y = xa trên khoảng (0 ; +oo)
a > 0
a < 0
Đạo hàm
y' = axa-1.
Chiều biến thiên
Hàm số luôn đồng biến.
Hàm số luôn nghịch biến.
Tiệm cận
Không có.
Tiệm cận ngang là trục Ox, tiệm cận đứng là trục Oy.
Đồ thị
Đồ thị luôn đi qua điểm (1 ; 1).
Bài tập
Tìm tập xác định của các hàm số :
a)y = (l-%) 3;	b)y = (2-x2)5;
c) y = (x2-l)-2;	d) y = (x2 - X - 2)Ạ/2 .
Tính đạo hàm của các hàm số :
I	..	„	,1
y = (2xz - X + l)	- KHÁI NIỆM LÔGARIT
1
 iTìm X để :
 a)2*=8;	b)2x=ị;	c)3*=81;
;	.	b) y = (4 - X - X2)
Cho số a dương, phương trình
 aa = b
đưa đến hai bài toán ngược nhau :
 Biết a , tính b.
 ;
TU
c) y = (3x + 1)2 ;	d) y = (5 - xỴ^.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số :
4
a) y = X3 ;	b) y = X-3.
Hãy so sánh các số sau với 1 :
a)(4,l)2’Biết b , tính a.
;	b)(0,2)°’3;
c) (0,7)3’2;	d) (73 )°’4.
Hãy so sánh các cặp số sau :
a) (3,1)7'2 và (4,3)7’2 ; b) Qỹ) ' và	; c) (0,3)Mvà (0,2)w ;