Giải toán 11 Bài 1. Đại cương về dường thẳng và mặt phẳng

§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THANG và mặt phang
A. KIẾN THỨC Cơ BẢN
Các tính chất
Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tính chất 4: Tồn tại bôn điểm không cùng thuộc một mặt phẵng.
Tính chất 5: Nếu hai mặt phẳng phân biột có một điểm chung thì chúng còn có một điểm chung khác nữa.
Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
Cách xác định một mặt phẳng
Bôn cách xác định mặt phẳng
Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Hai đường thẳng song song.
Hình chóp và hình tứ diện
a) Hình chóp
Định nghĩa: Cho đa giác lồi AjA2 ... An và điểm s nằm ngoài mặt phẳng chứa đa giác đó. Nốì s với các đỉnh Aj,At,...,A để được n tam giác SA|A0, SA„A3,..., SAnAj.
Hình gồm n tam giác đó và đa giác A(Aq... An gọi là hình chóp đỉnh s
và được kí hiệu là S.A.A,... A .
•	.	1	2 n
b) Hình tứ diện
Định nghĩa: Cho bốn điểm A, B, c, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD, BCD gọi là hình tứ diện (hay ngắn gọn là tứ diện) và được kí hiệu là ABCD. Thiết diện (hay mặt cắt) của hình eX'khi cắt bởi mp(P) là phần chung của mp(P) và hìnhe/iC
PHƯƠNG PHÁP GIẢI BÀI TẬP
Cho điểm A không nằm trên mặt phẵng (a) chứa tam giác BCD. Lấy E, F là các điểm lần lượt nằm tr, n cáccạnh AB, AC.
a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC).
b) Khi EF và BC cắt nhau tại 1, chứng minh 1 là điểm chung cùa hai mặt phẳng (BCD) và (DEF) éìiải
Ta có: E e AB nên E e (ABC)
Fe AC nên F e (ABC). Suy ra EF nằm trong (ABC).
I e BC => I e (BCD).
I e EF => I 6 (DEF).
Vậy I e (BCD) n (DEF).
Gọi M là giao điểm của đường thẳng (J và mặt phẵng (a). Chứng minh M là điểm chung của (a) vđi một mặt phẵng bất kì chứa li.
Ốịiải
Hiển nhiên M e (a). Gọi (P) là mặt. phẳng bất kì chứa d, ta có
ÍM G d Ịdc(P)
=> M G (P).
Vậy M là điểm chung của (a) và mọi mặt phẩng (P) chứa d.
Cho ba đường thẳng di, da, di không cùng nằm trong một mặt phẫng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy.
tfiai
Giả sử I = dj nd2. Ta chứng minh I e d3.
Nếu d3 không đi qua I thì d3 cắt di và d2 lần lượt tại J và K (khác I).
J, K không thẳng hàng nên tạo thành mặt phẳng (IJK). Khi đó d|, d2, d3 nằm trong (IJK) (vô lí). Vậy d3 đi qua I tức d), d2, d3 đồng quy.
Cho bô'n điểm A, B, c và D không đồng phẩng. Gọi Ga, Gn, Gc, G|, lần lượt là trọng tâm của các tam giác BCD, CDA, ABD, ABC. Chứng minh ràng AGa, BGii, CGc, DG|) đồng quy.
G"A
G"Ga
Lí luận tương tự, ta có CGc, DGp cũng cắt AGa tại G', G"
Như vậy G = G' = G"
Ghi chú: Ta gọi AGa, BGg, CGc và DGd là các đường trung tuyến và G là trọng tâm của tứ diện ABCD.
Cho tứ giác ABCD nằm trong mặt phẳng (a) có hai cạnh AB và CD không song song. Gọi s là điểm nằm ngoài ntặt phẳng (a) và M là trung điểm đoạn sc.
Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB).
Gọi o là giaưđiểm cùa AC và BD. Chứng minh rằng ba đường thẳng so, AM, BN đồng quy.
b)
a)
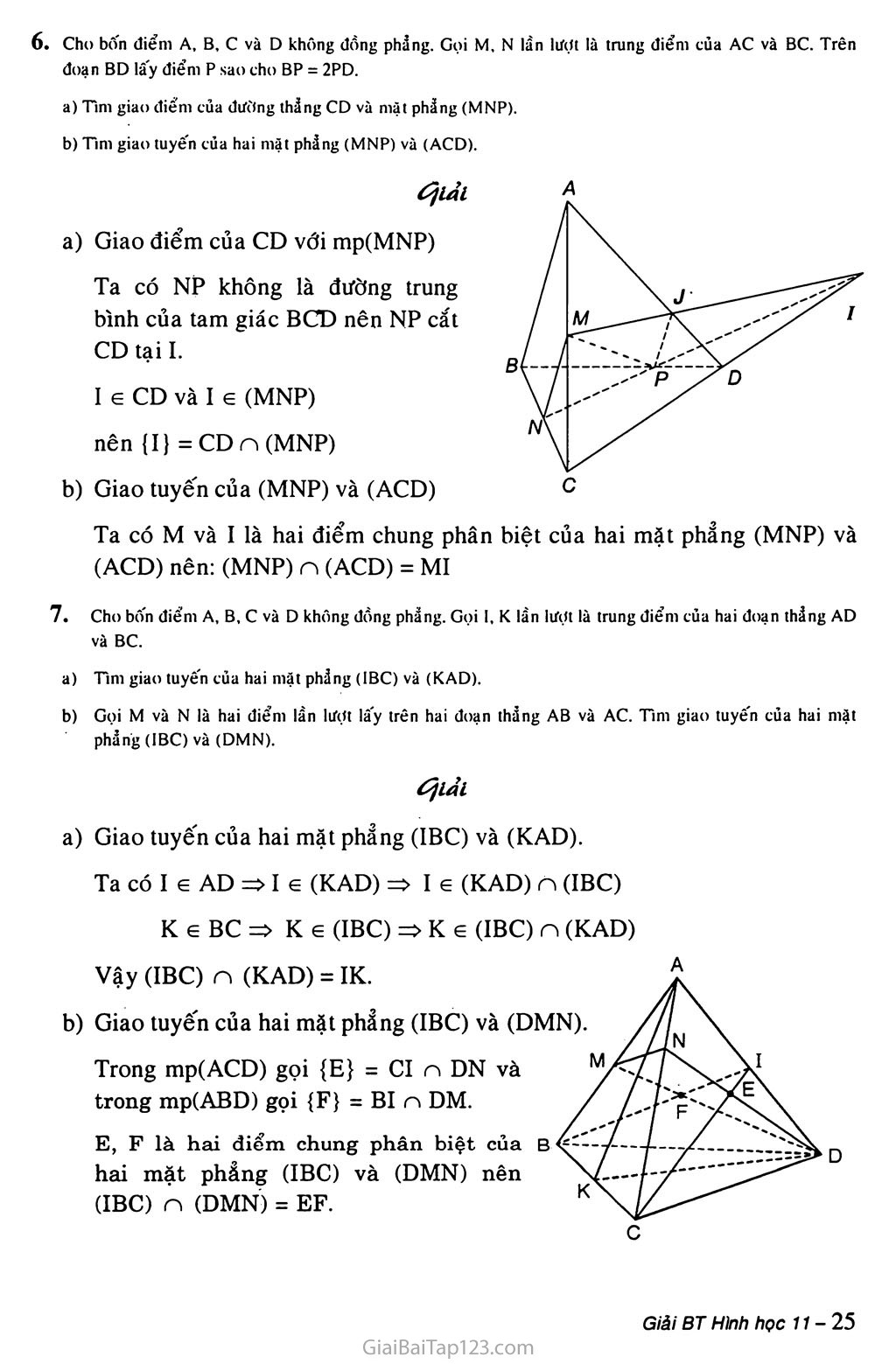
Cho bốn điểm A, B, c và D không đồng phẩng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lâ'y điểm p sao cho BP = 2PD. a) Tìm giao điểm của dưìtng thẳng CD và mặt phẫng (MNP).
b) Tim giao tuyến của hai mặt phẳng (MNP) và (ACD).
biệt của hai mặt phẳng (MNP) và
ốỳẦl
Giao điểm của CD với mp(MNP)
Ta có NP không là đường trung bình của tam giác BCD nên NP cắt CD tại I.
I e CD và I e (MNP) nên {1} = CD n (MNP)
Giao tuyến của (MNP) và (ACD)
Ta có M và I là hai điểm chung phâ (ACD) nên: (MNP) n (ACD) = MI
Cho bốn điểm A, B, c và D không đồng phẵng. Gọi 1, K lần lượt là trung điểm của hai đoạn thẳng AD và BC.
Tim giao tuyến của hai mặt phảng (1BC) và (KAD).
Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (1BC) và (DMN).
tfiai
Giao tuyến của hai mặt phẳng (IBC) và (KAD).
Ta có I e AD => I e (KAD) => I e (KAD) n (IBC) K e BC => Ke (IBC) => K e (IBC) n (KAD)
Vậy (IBC) n (KAD) = IK.
Giao tuyến của hai mặt phẳng (IBC) và (DMN).
Trong mp(ACD) gọi {E} = CI n DN và trong mp(ABD) gọi {F} = BI n DM.
E, F là hai điểm chung phân biệt của B hai mặt phẳng (IBC) và (DMN) nên (IBC) n (DMN) = EF.
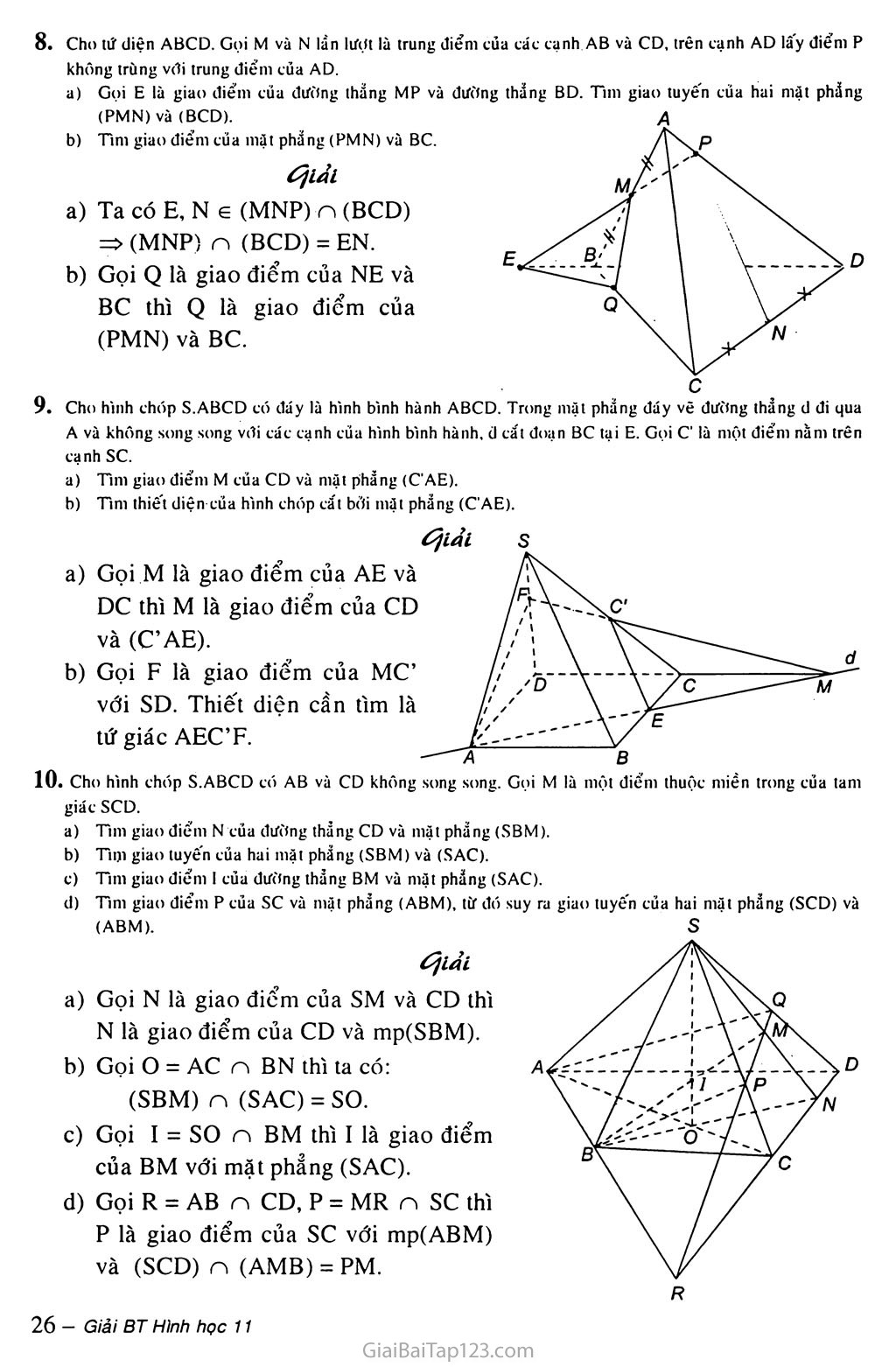
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm tủa tát tạnh AB và CD, trên tạnh AD lây điểm p không trùng với trung điểm tủa AD.
a) Gọi E là giao điểm tủa đường thẳng MP và đường thẳng BD. Tim giao tuyến tủa hai mặt phẵng
(PMN) và (BCD).
b) Tìm giao điểm tủa mặt phẩng (PMN) và BC.
Ốịlằl
Ta có E, N e (MNP) n (BCD)
=> (MNP) n (BCD) = EN.
9.
Gọi Q là giao điểm của NE và BC thì Q là giao điểm của (PMN) và BC.
Cho hình thóp S.ABCD tó đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đưìtng thẳng d di qua A và không song song vói tát tạnh tủa hình bình hành, d tắt đoạn BC lại E. Gọi C' là một điểm nằm trên tạnh sc.
Tim giao điểm M tủa CD và mặt phẵng (CAE).
Tim thiết diện tủa hình thóp tắt bói mặt phăng (C'AE).
Gọi M là giao điểm của AE và DC thì M là giao điểm của CD và (C’AE).
Gọi F là giao điểm của MC’ với SD. Thiết diện cần tìm là tứ giác AEC’F.
10. Cho hình thóp S.ABCD tó AB và CD không song song. Gọi M là một điểm thuật miền trong tủa tam giát SCD.
Tim giao điểm N tủa đường thẳng CD và mặt phẫng (SBM).
TÌI)1 giao tuyến tủa hai mặt phẵng (SBM) và (SAC).
t) Tìm giao điểm I tủa đưítng thăng BM và mặt phăng (SAC).
d) Tìm giao điểm p tủa sc và mặt phẫng (ABM), từ đó suy ru giao tuyến tủa hai mặt phẳng (SCD) và (ABM).	s
(yỊiải
Gọi N là giao điểm của SM và CD thì N là giao điểm của CD và mp(SBM).
Gọi o = AC n BN thì ta có:
(SBM) n (SAC) = SO.
Gọi 1 - SO n BM thì I là giao điểm của BM với mặt phẳng (SAC).
Gọi R = AB n CD, p = MR n sc thì p là giao điểm của sc với mp(ABM) và (SCD) n (AMB) = PM.
c. BÀI TẬP LÀM THÊM
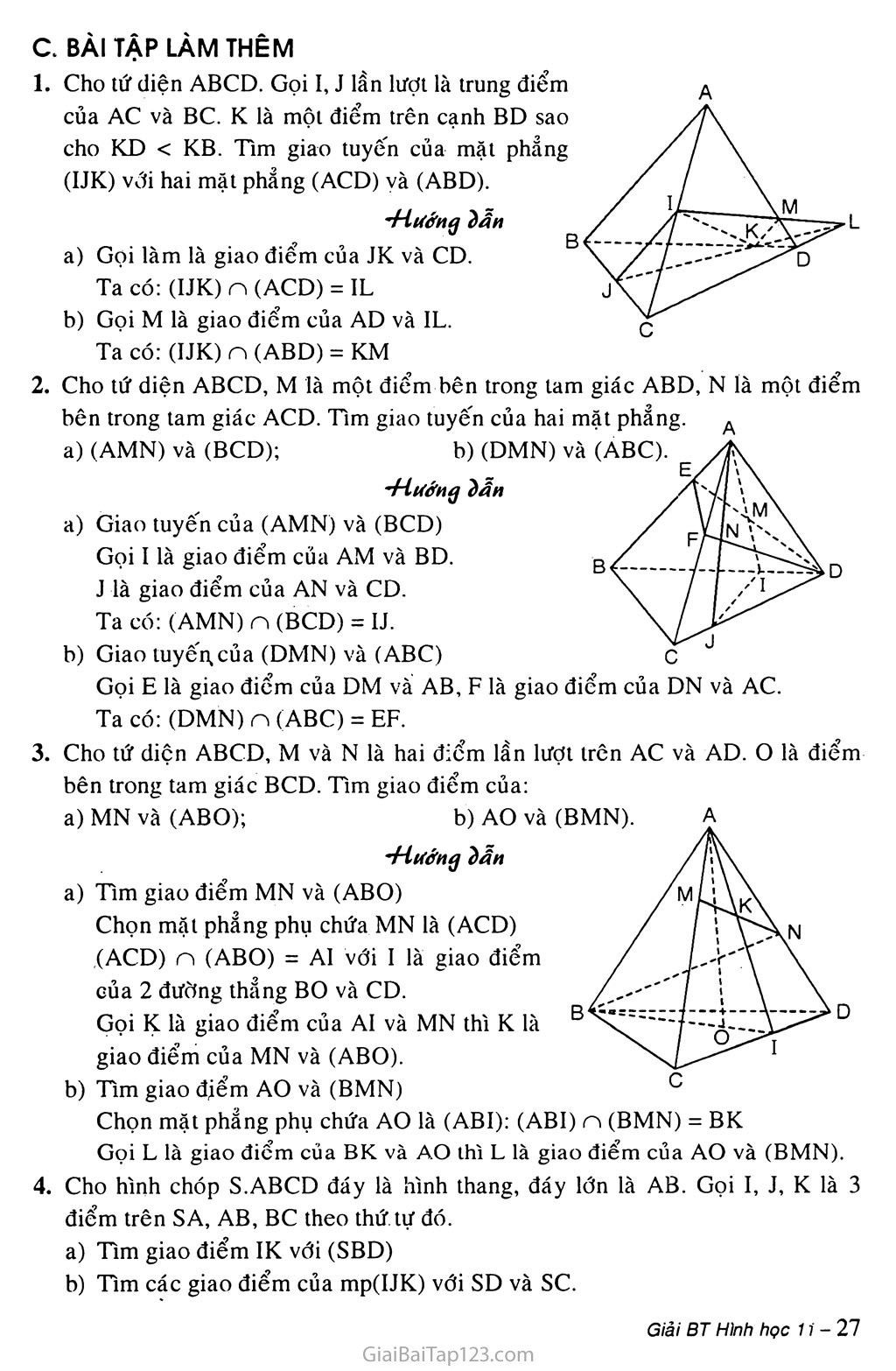
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. K là một điểm trên cạnh BD sao cho KD < KB. Tìm giao tuyến của mặt phẳng (IJK) với hai mặt phẳng (ACD) và (ABD).
•Hưởng iẫn
Gọi làm là giao điểm của JK và CD.
Ta có: (IJK) n (ACD) = IL
Gọi M là giao điểm của AD và IL.
Ta có: (IJK) n (ABD) = KM
Cho tứ diện ABCD, M là một điểm bên trong tam giác ABD, N là một điểm
bên trong tam giác ACD. Tìm giao tuyến của hai mặt phẳng. a) (AMN) và (BCD);	b) (DMN) và (ABC).
Hưởng iẫn
Giao tuyến của (AMN) và (BCD)
Gọi I là giao điểm của AM và BD.
J là giao điểm của AN và CD.
Ta co: (AMN) n (BCD) = 1J.
Giao tuyến,của (DMN) và (ABC)
Gọi E là giao điểm của DM và AB, F là giao điểm của DN và AC.
Ta có: (DMN) n (ABC) = EF.
Cho tứ diện ABCD, M và N là hai điểm lần lượt trên AC và AD. o là điểm bên trong tam giác BCD. Tìm giao điểm của:
a) MN và (ABO);	b) AO và (BMN).
Hưởng ìẫn
Tìm giao điểm MN và (ABO)
Chọn mặt phẳng phụ chứa MN là (ACD)
(ACD) n (ABO) = AI với I là giao điểm của 2 đường thẳng BO và CD.
Gọi K là giao điểm của Aỉ và MN thì K là B giao điểm của MN và (ABO).
Tìm giao điểm AO và (BMN)
Chọn mặt phẵng phụ chứa AO là (AB1): (ABI) n (BMN) = BK Gọi L là giao điểm của BK và AO thì L là giao điểm của AO và (BMN).
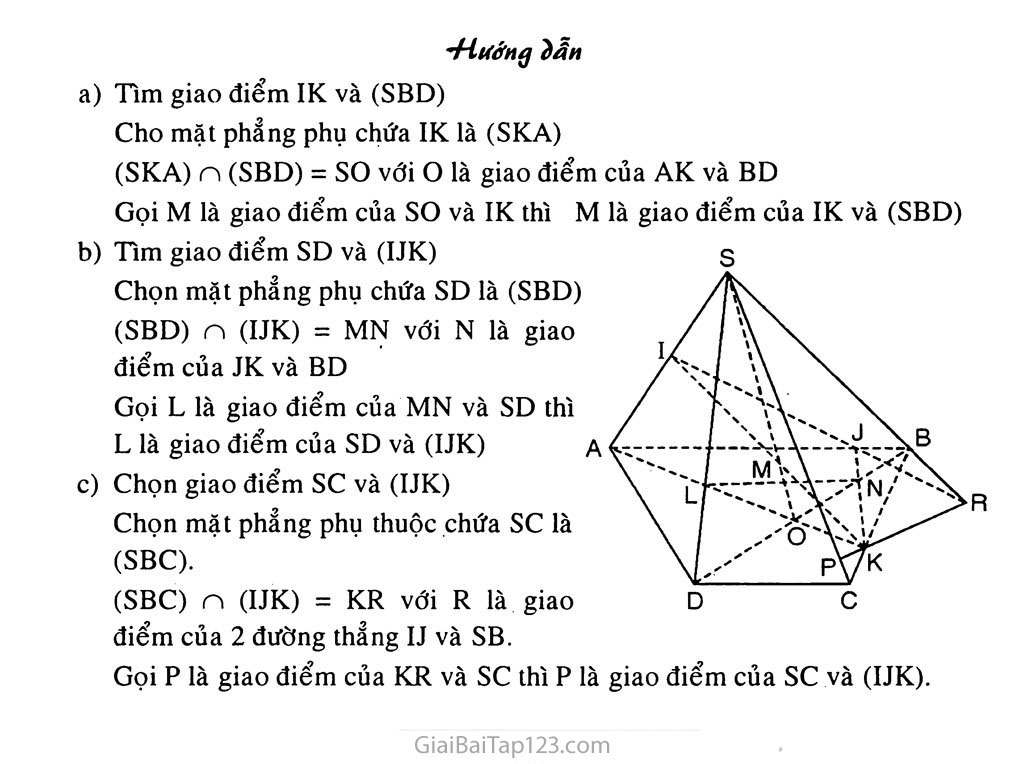
Cho hình chóp S.ABCD đáy là hình thang, đáy lớn là AB. Gọi I, J, K là 3 điểm trên SA, AB, BC theo thứ. tự đó.
Tìm giao điểm IK với (SBD)
Tìm các giao điểm của mp(IJK) với SD và sc.
-Hướng ìẫn
Tim giao điểm IK và (SBD)
Cho mặt phẳng phụ chứa IK là (SKA)
(SKA) n (SBD) = SO với o là giao điểm của AK và BD
Gọi M là giao điểm của so và IK thì M là giao điểm của IK và (SBD)
Tim giao điểm SD và (IJK)
Chọn mặt phẳng phụ chứa SD là (SBD)
(SBD) n (IJK) = MN với N là giao điểm của JK và BD
Gọi L là giao điểm của MN và SD thì L là giao điểm của SD và (IJK)
Chọn giao điểm sc và (IJK)
Chọn mặt phẳng phụ thuộc chứa sc là (SBC).
(SBC) n (IJK) = KR với R là giao điểm của 2 đường thẳng IJ và SB.
Gọi p là giao điểm của KR và sc thì p là giao điểm của sc và (IJK).