Giải toán 11 Bài 5. Khoảng cách

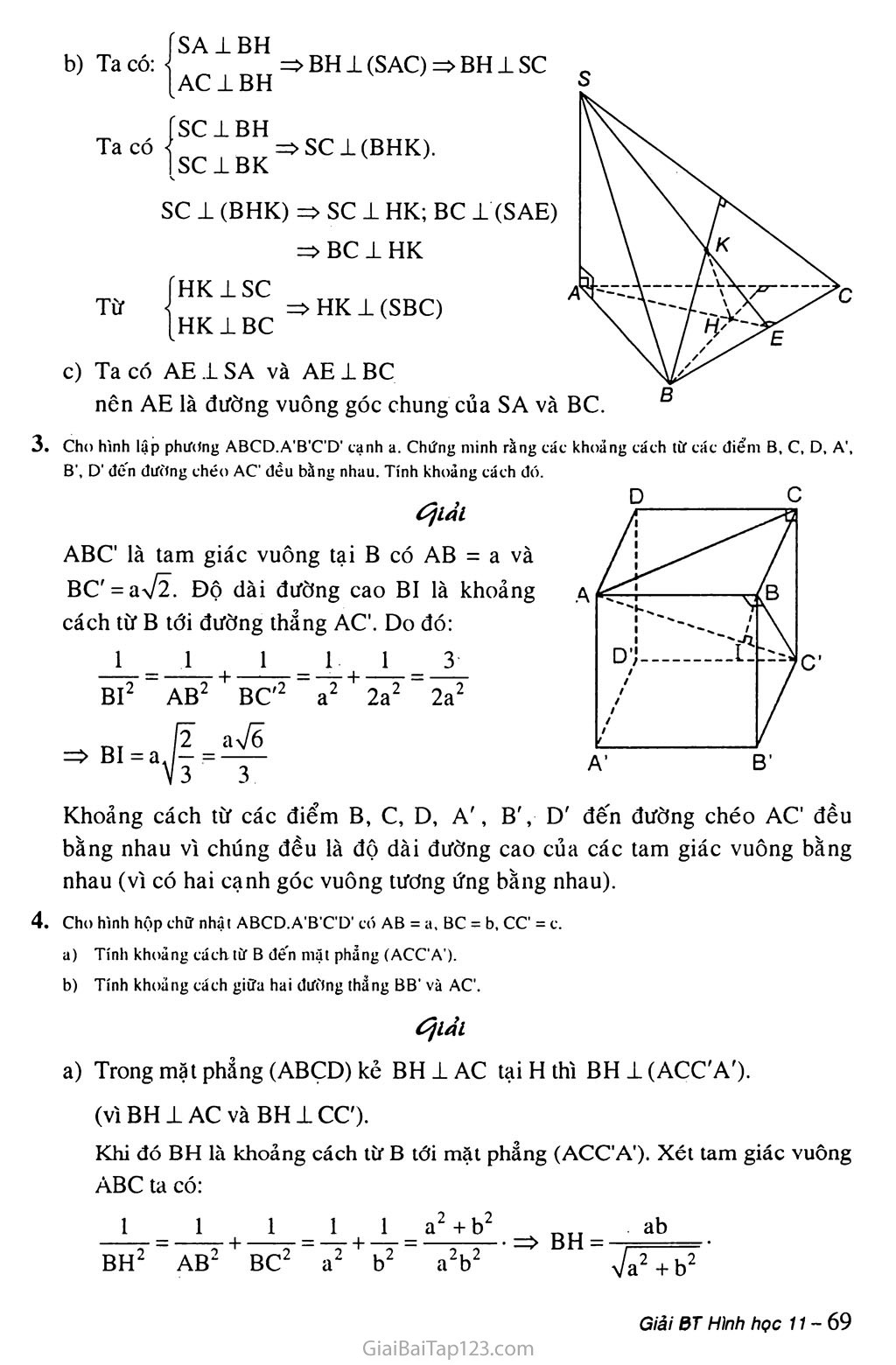
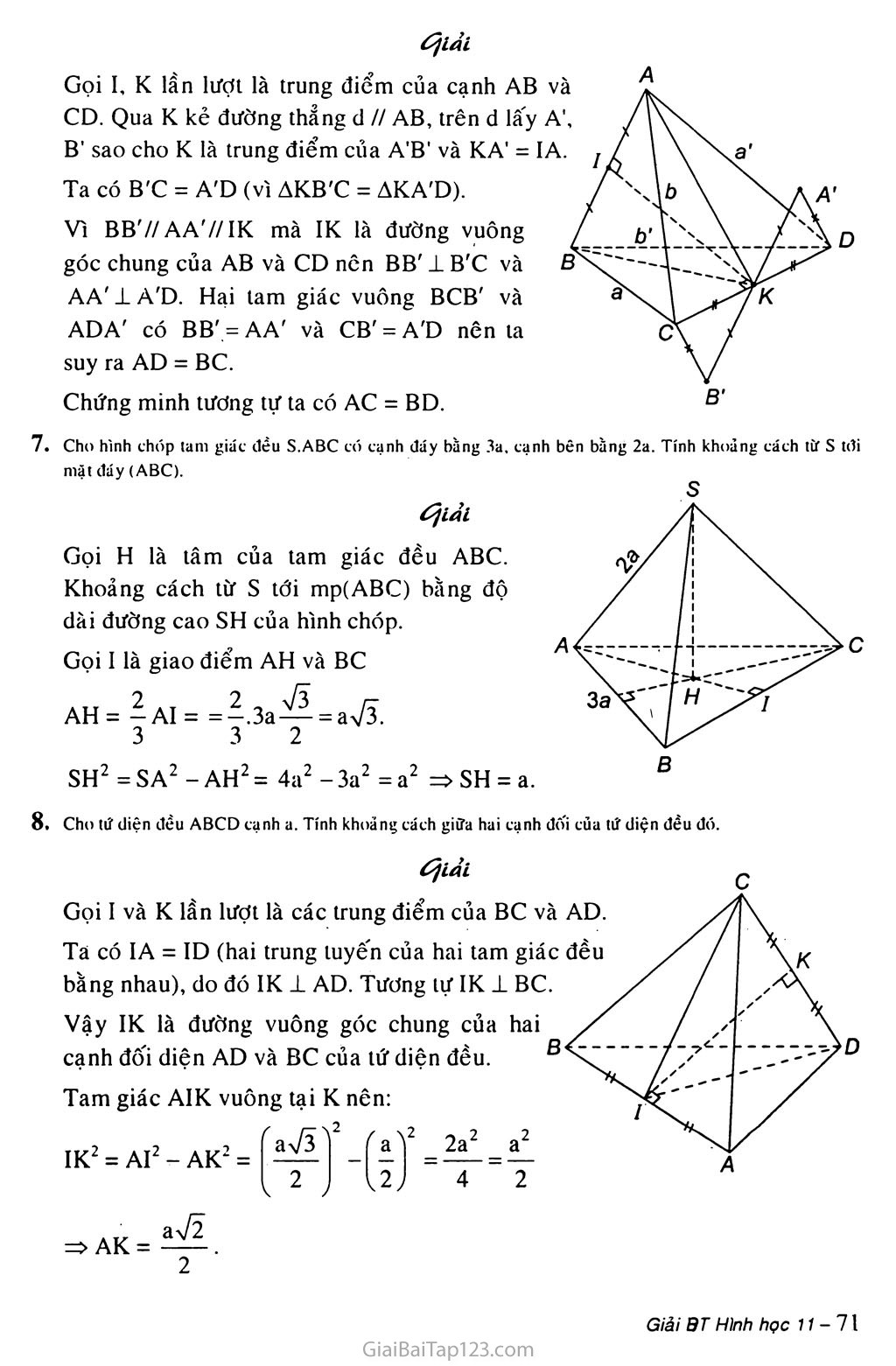
§5. KHOẢNG CÁCH
A. KIẾN THỨC Cơ BẢN
Định nghĩa 1
Khoảng cách từ điểm M đến mặt phẳng (P) (hoặc đến đường thẳng A) là khoảng cách giữa hai điểm M và H trong đó H là hình chiếu của điểm M trên mặt phẳng (P) (hoặc trên đường thẳng A).
Định nghĩa 2
Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm nào đó của a đến mặt phẳng (P).
Định nghĩa 3
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia,
Định nghĩa 4
Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó.
* Cách tính khoảng cách giữa hai đường thẳng chéo nhau
Giả sử a và b là hai đường chéo nhau và a 1 b.
Ta dựng mặt phẳng (a) chứa a và vuông góc với b tại B.
Trong (a) dựng BA ± a tại A, ta được độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Giả sử a và b là hai đường thẳng chéo nhau nhưng không vuông góc với nhau.
Cách 1:
Ta dựng mặt phẳng (oc) chứa a và song song với b.
Lấy một điểm M tùy ý trên b dựng MM' ± (a) tại M':
Từ M' dựng b' // b cắt a tại A.
Từ A dựng AB // MM' cắt b tại B, độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Cách 2:
Ta dựng mặt phẳng (a) 1 a tại o, (a) cắt b tại I.
Dựng hình chiếu vuông góc của b là b’ trên (a).
Trong mặt phẳng (a), vẽ OH lb1, H Ễ b'.
Từ H dựng đường thẳng song song với a cắt b tại B.
Từ B dựng đường thẳng song song với OH cắt a tại A.
Độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Trong cát mệnh dề sau đây mệnh đề nào là đúng ?
Đường thẳng A là đường vuông góc chung của hai đường thẳng a và b nếu A vuông góc vdi a và A vuông góc với b.
Gọi (P) là mặt phảng song song vởi cả hai đường thẳng a, b chéo nhau. Khi đó đường vuông góc chung A của a và b luôn luôn vuông góc vdi (P).
Gọi A là đường vuông góc chung cùa hai đường thẳng chéo nhau a và b thì A là giao tuyến của hai mặt phẩng (a, A) và (b, A).
Cho hai đưílng thẳng chéo nhau a và b. Đường thẳng nào đi qua một điểm M trên a đồng thời cắt b tại N và vuông góc vói b thì dó là dường vuông góc chung của a và b.
Đường vuông góc chung A của hai đường thẳng chéo nhau a và b nằm trong mặt phảng chứa đưỉlng này và vuông góc với đường kia.
‘TíV? lời: a) Sai; b) Đúng; c) Đúng; d) Sai; e) Sai.
Cho tư diện S.ABC có SA vuông góc vdi mặt phẵng (ABC). Gọi H, K lần lượt là trực tâm cùa các tam giác ABC và SBC.
Chứng minh ba đường thẳng AH, SK. BC đồng quy.
Chứng minh rằng SC vuông góc vdi mặt phẵng (BHK) và HK vuông góc vời mật phảng (SBC).
Xác định đường vuông góc chung cùa BC và SA.
éjiải
Gọi E là giac điểm của AH và BC.
Ta có SA±(ABC)=>SA±BC.
ÍBC1AE
O ' ^BCl(SAE) => BC ± se. [BC1SA
Vậy ba đường thẳng AH, SK, BC đồng quy tại E.
b) Ta có:
• BH1 (SAC) => BH1 SC
SA1BH AC1BH
Ta có
Từ
■SCl(BHK).
SC1BH SC1BK
SC 1 (BHK) => sc 1 HK; BC 1 (SAE)
=> BC 1 HK
„„ =>HK±(SBC)	x A-
HK1BC
Ta có AE 1 SA và AE1BC
nên AE là đường vuông góc chung của SA và BC.
Cho hình lập phương ABCD.A'B'C’D' tạnh a. Chứng minh rằng cát khoảng tách tư tát điếm B, c, D, A', B', D' đến đương chéo AC' đều bằng nhau. Tính khoảng tách đó.
Ốịlải
1
BI2 -
BI = a
AB2 2 _
ABC' ià tam giác vuông tại B có AB = a và BC' = aự2. Độ dài đường cao BI là khoảng cách từ B tới đường thẳng AC'. Do đó:
2a2
' BC'2 a2 + 2a2
a Tó 3
Khoảng cách từ các điểm B, c, D, A', B', D' đến đường chéo AC đều bằng nhau vì chúng đều là độ dài đường cao của các tam giác vuông bằng nhau (vì có hai cạnh góc vuông tương ứng bằng nhau).
Cho hình hộp chữ nhật ABCD.A’B’C'D’ tó AB = a, BC = b, CC' = t.
Tính khoảng cách từ B đến mặt phẩng (ACCA’).
Tính khoảng cách giữa hai đương thẳng BB' và AC.
Ốjiảí
Trong mặt phẳng (ABCD) kẻ BH 1 AC tại H thì BH 1 (ACCA').
(vì BH 1 AC và BH1CC).
Khi đó BH là khoảng cách từ B tới mặt phẳng (ACCA’). Xét tam giác vuông ABC ta có:
1	1 _a2+b2
a2 + b2’ a2b2
1	11	1	1 a2 + b2	ab
Ta2+b2
BH2 AB2 BC
+ -
b) Mặt phẳng (ACCA') chứa AC và song song với BB' nên khoảng cách giữa BB' và AC’ chính là ab
khoảng cách BH
2+b!
5. Cho hình lập phương ABCD.A'B'C'D
Chứng minh rằng B’D vuông góc vơi mặt phẵng (BA'C).
Tính khoảng cách giữa hai mặt phẫng (BA'C) và (ACD').
Tính khoảng cách giữa hai đương thăng BC' và CD'.
a) Ta có:
Từ
A'C’IB'D'
A'C'IDD
BC'IB'C BC' 1 DC : DB'1 A'C'
, => A'C' 1 (BB'D'D) =} A'C' 1 DB'
BC' 1 (DCB'A') => BC' 1 DB'
DB'l(BA'C')
DB'IBC'
b) Hai mặt phẳng (BAC) và (ACD’) có BC7/AD'
A’C' // AC
(BA'C')//(ACD')
Gọi I và H lần lượt là giao điểm của DB' với D'O và BO'. Trong hình chữ nhật DBB'D' ta có
DI = ị IB'và B'H = -^-DH nên DI = IH = HB'= ỊdB'=> 1H = ^5- 2	2	3	3
a /3
Vậy khoảng cách giữa hai mặt phẳng (BA'C) và (ACD') là ——-•
c) Khoảng cách giữa hai đường thẳng chéo nhau BC và CD’ bằng khoảng cách giữa hai mặt phẳng song song (BA'C) và (ACD’) lần lượt chứa hai
đường thẳng chéo nhau đó. Ta suy ra khoảng cách giữa hai đường thẳng /7	'
BC'và CD' là (1=^7—•
3
6. Chứng minh rằng nếu dương thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là dương vuông góc chung của AB và CD thì AC = BD và AD = BC.
Ốịlải
Gọi I, K lần lượt là trung điểm của cạnh AB và CD. Qua K kẻ đường thẳng d // AB, trên d lấy A',
B’ sao cho K là trung điểm của A'B' và KA' = IA. Ị Ta có B'C = A'D (vì AKB'C = AKA'D).
Vì BB7/AA7/IK mà IK là đường vuông góc chung của AB và CD nên BB' 1 B'C và AA' 1 A'D. Hại lam giác vuông BCB' và ADA' có BB' = AA' và CB' = A'D nên la suy ra AD = BC.
Chứng minh tương tự ta có AC = BD.
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách lừ s tdi mặt đáy (ABC).
Ốịlảl
Cọi H là tâm của tam giác đều ABC.
Khoảng cách từ s tới mp(ABC) bằng độ dài đường cao SH của hình chóp.
Gọi I là giao điểm AH và BC
AH= |aI= = |.3a^ = aự3.
3	3	2
SH2 = SA2 - AH2 = 4a2 - 3a2 = a2 => SH = a.
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối của tứ diện đều đó.
-yD
Ốịiải
Gọi I và K lần lượt là các trung điểm của BC và AD.
Ta có IA = ID (hai trung luyến của hai tam giác đều bằng nhau), do đó IK 1 AD. Tương lự IK 1 BC.
Vậy IK là đường vuông góc chung của hai cạnh đối diện AD và BC của tứ diện đều.
1^3
2a2
Tam giác AIK vuông tại K nên:
IK2 = AI2 - AK2 =
=> AK = —— .
c. BÀI TẬP LÀM THÊM
Trong hai mặt phẳng vuông góc (P) và (Q) cho hai tam giác cân ACD và BCD có chung đáy CD = 2x và các cạnh khác có độ dài a. Gọi M và N là trung điểm của AB và CD.
Chứng minh rằng MN là đường vuông góc chung của AB và CD.
Tính theo a và X độ dài các đoạn AB và MN.
Tứ diện OABC có OA = OB = oc = a và ẤÕÌ = Ấõc = 60°; BOC = 90°.
Tính độ dài các cạnh còn lại của tứ diện và chứng minh rằng ABC là tam giác vuông.
Chứng minh OA ± BC, gọi I, J lần lượt là trung điểm của OA và BC, chứng minh rằng IJ là đường vuông góc chung của OA và BC.
Chứng minh rằng (ABC) JL (BOC). Tính độ dài đoạn IJ theo a.