Giải toán 11 Bài 1. Vectơ trong không gian

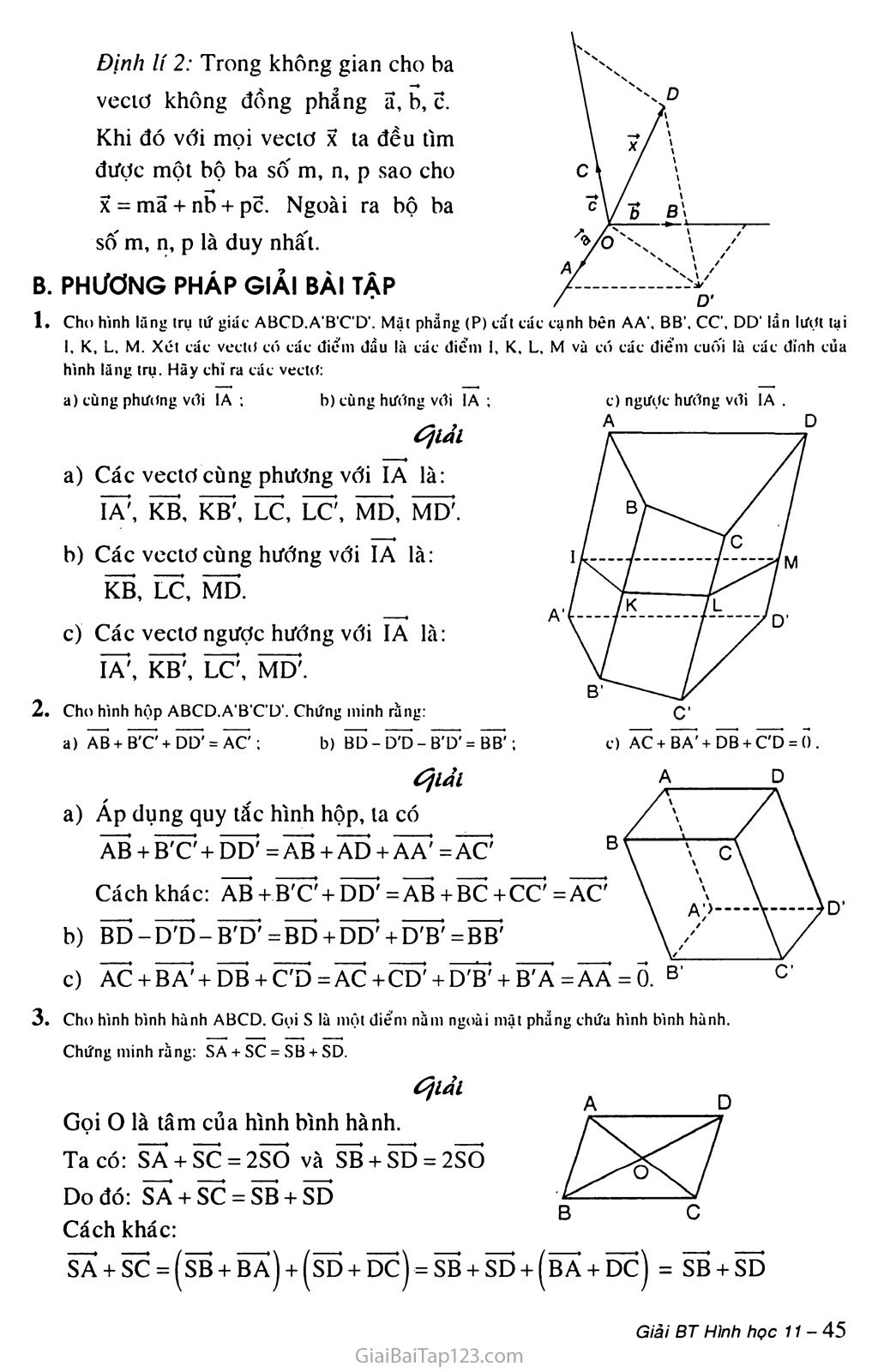
§1. VECTƠ TRONG KHÔNG GIAN
A. KIẾN THỨC Cơ BẢN
Định nghĩa và các phép toán về vectơ trong không gian
Địnli nghĩa: Vcctơ trong không gian là một đoạn thẳng có hướng. Kí hiệu AB chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn đưực kí hiệu là ẩ, b, x, ỹ,...
Phép cộng vù phép trừ vectơ trong không gian: Phép cộng và phép trừ hai vectơ trong không gian được định nghĩa tương tự như phép cộng và phép trừ hai vectơ trong mặt phẳng. Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng. Khi thực hiện phép cộng vcctư trong không gian ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong hình học phẳng.
Quỵ tắc hình hộp: Nếu hình hộp	ễ-	-ỹỵ
gian, tích của vectơ a với một số k 0 là vectrt kã được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các lính chất đã đưực xét trong mặt phẳng.
Điều kiện đồng phẳng của ba vectơ
Định nghĩa: Trong không gian ba vcctơ đưực gọi là đồng phăng nếu các giá của chúng cùng song song với một mặt phẳng.
h) Điều kiện để ha vectơđồng phổng
Định lí 1: Trong không gian cho hai vectơ ã, b không cùng phương và vectơ C. Khi đó ba vectơ ã, b, C đồng phẳng khi và chỉ khi có cặp sô" m, n sao cho C = mã + nb.
Ngoài ra cặp sô" m, n là duy nhâ"t.
t) AC + BA'+DB + C'D = 0 .
Định lí 2: Trong khôr.g gian cho ba veciư không đồng phẳng a, b, C. Khi đó với mọi vectơ X ta đều tìm được một bộ ba số m, n, p sao cho X = mã + nb + pc. Ngoài ra bộ ba số m, n, p là duy nhất.
PHƯƠNG PHÁP GIẢI BÀI TẬP
Cho hình lãng trụ tứ giát ABCD.A’B'C’D'. Mặt phăng (P) tắt tát tạnh bên AA', BB'. cc, DD' lần lượt tại I. K, L, M. Xét tát vettil tó tát điểm dầu là tát điểm I, K, L. M và tó tát điểm tuôi là tát đính tủa
hình lăng trụ. Hãy thi ra tát veetơ:
a) tùng phương vói IA ;	b)tùng hương vơi IA ;
éjiải
Các vectơ cùng phương với IA là:
ĨÃ\ KB, KB\ LC, LC, MD, MO'.
Các vcctơ cùng hướng với IA là:
KB, LC, MD.
Các vectơ ngược hướng với IA là:
ĨA', KB5, LC', MD1.
Chơ hình hộp ABCD.A’B'C'D'. Chứng minh rằng:
a) ÃB + ữc' + 5ữ = ÃC'; b) BD - ữõ - ữữ = BB';
éịiải
Áp dụng quy tắc hình hộp, ta có ÃB + BC + DD5 =ÃB + ÃD + Ã7? =ÃƠ Cách khác: ÃB +BV + ĐÔ' =ÃB + BC + CC =ĂƠ
bd-d;d-b7d:=bd + dd; + d7b:=bb''
ac + bX'+db + c7d=ac+cd;+d7b; + b7a=aa = 0. B
Chơ hình bình hành ABCD. Gợi s là một điểm nằm ngơài mặt phẵng thứa hình bình hành. Chứng minh rằng: SA + SC = SB + SD.
Ốjiải
Gọi o là tâm của hình bình hành.
Ta có: SA + SC-2SO và SB + SD = 2SO Do đó: SA + SC = SB + SD
Cách khác: sa + sc = (sb + ba) + (sd + dc) = sb + sd + (ba + dc) = sb + sd
4. Cho hình tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng:
A	"
a) MN = ị(AD+BC);	b) MN = ị(ÃC + BD).
ỐỊiải
2 2
a) Ta có:
MN=MA+AD + DN
MN=MB + BC+CN
mn=|(ad + bc).
b) Tương tự:
MN=MA + AC+CN MN=MB + BD + DN Suy ra 2MN = (ma + mb) + (Ãc + Bd) + (cN + Dn) = AC + BD
=>MN = |(AC + BD).
Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho: a) AE = AB +AC +AD ;	b) ÃẼ = AB +Ãẽ - AD.
ỐịiĂi
a) Ta có AE=AB+AC+AD mà (ÃB + ÃC) +ĂD =ÃG + AD với G là đỉnh thứ tư của hình bình hành ABGC vì AG =AB + AC.
Vậy AE = AG+AD với E là đỉnh thứ tư của hình bình hành AGED. Do đó AE là đường chéo của hình hộp có ba cạnh là AB, AC, AD.
Ta có ÃF=(ÃB + Ăc)-ÃD = AG-AD = DG.
Vậy F là đỉnh thứ tư của hình bình hành ADGF.
Cho hình tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC.
Chứng minh rằng: DA + DB + DC = 3DG.
Ốịlảl
G là trọng tâm tam giác ABC nên GA + GB +GC =Õ.
Tacó DA + DB + DC = (dG + GÃ) + (dG + Gb) + (5g + Gc)
= 3DG + (ga + GB+ Gc)=3DG
Gọi M và N lần lượi là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và p là một điểm bâì kì trong không gian. Chứng minh rằng:
a) 1A + IB+ IC+ 1D = 0 ;
Ốịlảl
b) Pl = ị(PA + PB + PC + PD). 4
Ta có IM+IN=Õ mà 2ĨM=ĨẤ+ĨC và 2ĨN=ĨB+ĨD nên 2(IM+IN)=Õ
suy ra IA + IB + IC+ ID =Õ
Với điểm p bất kì trong không gian ta có:
IA = PA-PI, IB = PB-PI IC = PC-PI, ID = PD-PI.
Vậy ĨA + ĨB + ĨC + ĨD = PA + PB + PC + PD-4PI mà theo câu a), ta có IA + IB + IC + ID =0 nên suy ra:
PI=4(PA + PB + PC + PD).
4
Cho hình lăng trụ lam giác ABC.A’B'C' có AA' = ã, AB = b, AC = c. Hãy phân tích (hay biểu thị) các vectư B'c, BC' qua các vectơ a, b, C.
tfiai
Ta có:
B'C = AC - ÃẼP = Ãc - (ÃÃ' + ÃB)
= c-ẵ-b
BC' = AC - ÃB = (ÃÃ' + ÃC) - ÃB = ẩ + c-b
Cho tam giác ABC. Lấy điểm s nằm ngoài mặt phẵng (ABC). Trên đoạn SA lây điểm M sao cho
MS = -2MA và trên đoạn BC lấy điểm N sao cho NB = -^NC.
Chứng minh rằng ba vectil AB, MN, sc dồng phẵng.
Ốịlảl
MN = MS + SC + CN	(1)
MN = MA + AB + BN •=> 2MN = 2MA + 2ÃB + 2BN	(2)
Cộng (1) với (2) ta được:
3MN = MS + 2MA + sc + 2AB + CN + 2BN.
0 0
Vậy MN=ỊsC + ỊãB.
3	3
Do đó ba vectd MN, sc, AB đồng phẳng.
Cho hình hộp ABCD.EFGH. Gọi K lù giao điểm của AH và DE, I là giao điểm của BH và DF. Chứng minh ba vectd AC. KI, FG dồng phầng.
Ốịiải
Ta có KI // EF // AB nên KI // mp (ABC),
FG // BC và AC c mp (ABC).
Do đó ba vẹctơ KI, FG, AC có giá cùng song song với một mặt phẳng (a) là mặt phẳng song song với mặt phẳng (ABC). Vậy ba vectơ KI, FG, AC đồng phẳng.
c. BÀI TẬP LÀM THÊM
Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB, AC, I là trung điểm của EF.
Chứng minh rằng IA + IB + IC + ID = 0 .
M bất kì trong không gian, chứng minh: 4 MI = MA + MB + MC + MD
Tìm M 6 (P) cố định sao cho ỊmA + MB + MC + Md| nhỏ nhất.
-Hưởng iẫn
ĨA + ĨB = 2ĨE, IC + ID = 2ĨF và IE + IF = õ .
Áp dụng quy tắc 3 điểm xen I vào vê phải.
Áp dụng câu b) |mA + MB + MC + Md| = 4Ịmi| nhỏ nhất khi M là hình chiếu vuông góc của I lên (P).
Cho hình hộp ABCD.A'B'C'D'. Gọi p, R lần lượt là trung điểm các cạnh AB, A’D, gọi P', Q, Q' lần lượt là giao điểm các đường chéo của các mặt ABCD, CDD'C, A'B'C'D, ADD'A'.
Chứng minh rằng: PP'+ QQ'+ RR'= õ .
Chứng minh rằng hai lam giác PQR, P'Q'R' có cùng trọng tâm.
-Hưởng dẫn
pF' = |aD, QQ^'-IeW, RR; = |a7A
2 2 2 = PT + ocr + RR^ |(ad+da' + a7a) = 0
Gọi G và G' lần lượt là trọng tâm APQR và AP'Q'R'. Áp dụng a) và hệ ba điểm suy ra: 3 GG' - õ
Cho hình hộp xiên ABCD.A'B'C’D. Gọi G là trọng tâm tam giác A'B'C'.
Chứng minh BD' = 3BG
Gọi p, Q, R là ảnh đối xứng của điểm D' qua các điểm A, B', c. Chứng tỏ rằng B là trọng tâm của tứ diện PQRD'.
-Hưởng dẫn
Áp dụng quy tắc trọng tâm 3 BG = BA + BB' + BC = BD'
Chứng minh BP + BQ + BR + BD'= õ