Giải toán 11 Bài 4. Hai mặt phẳng song song

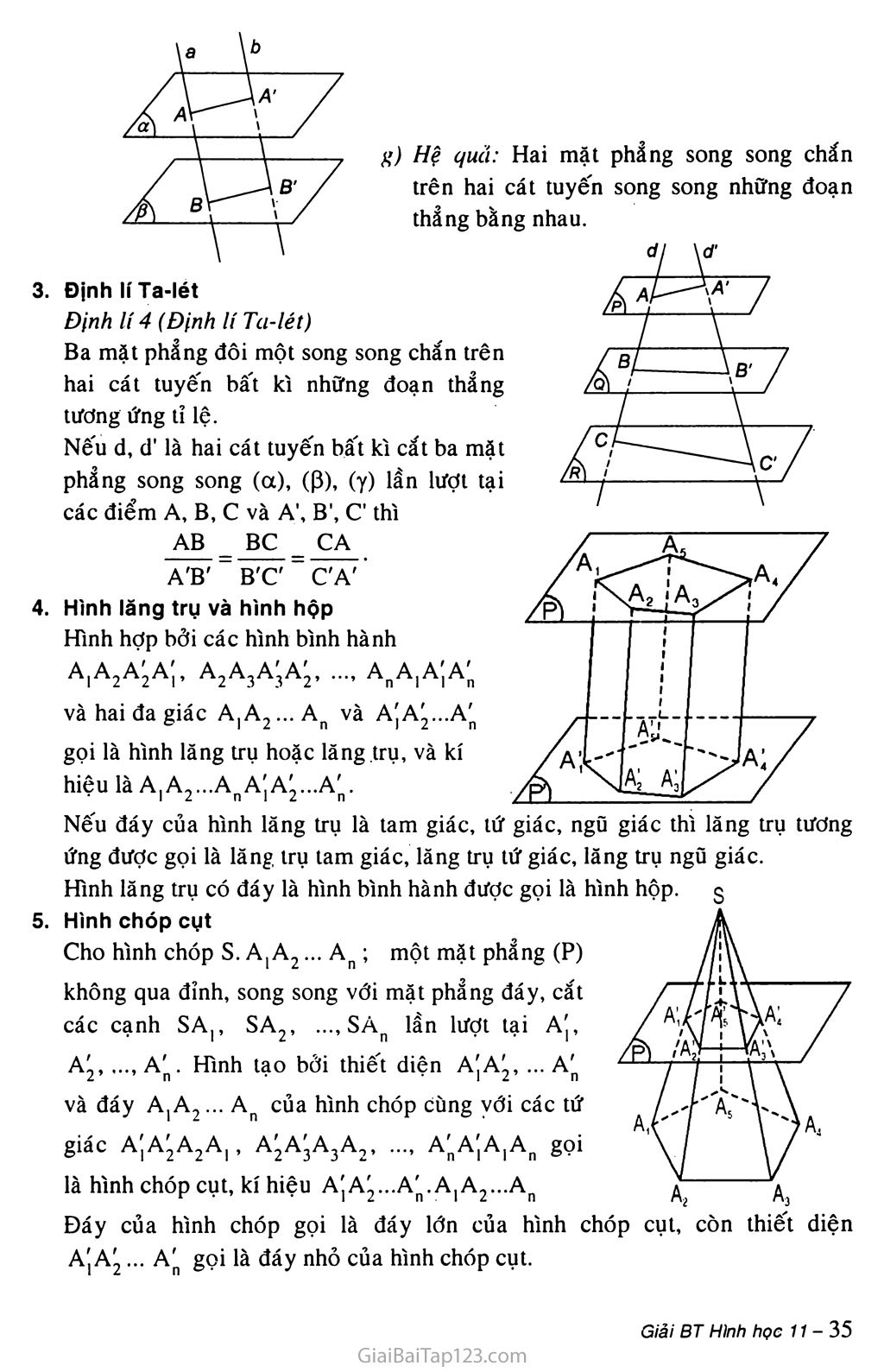
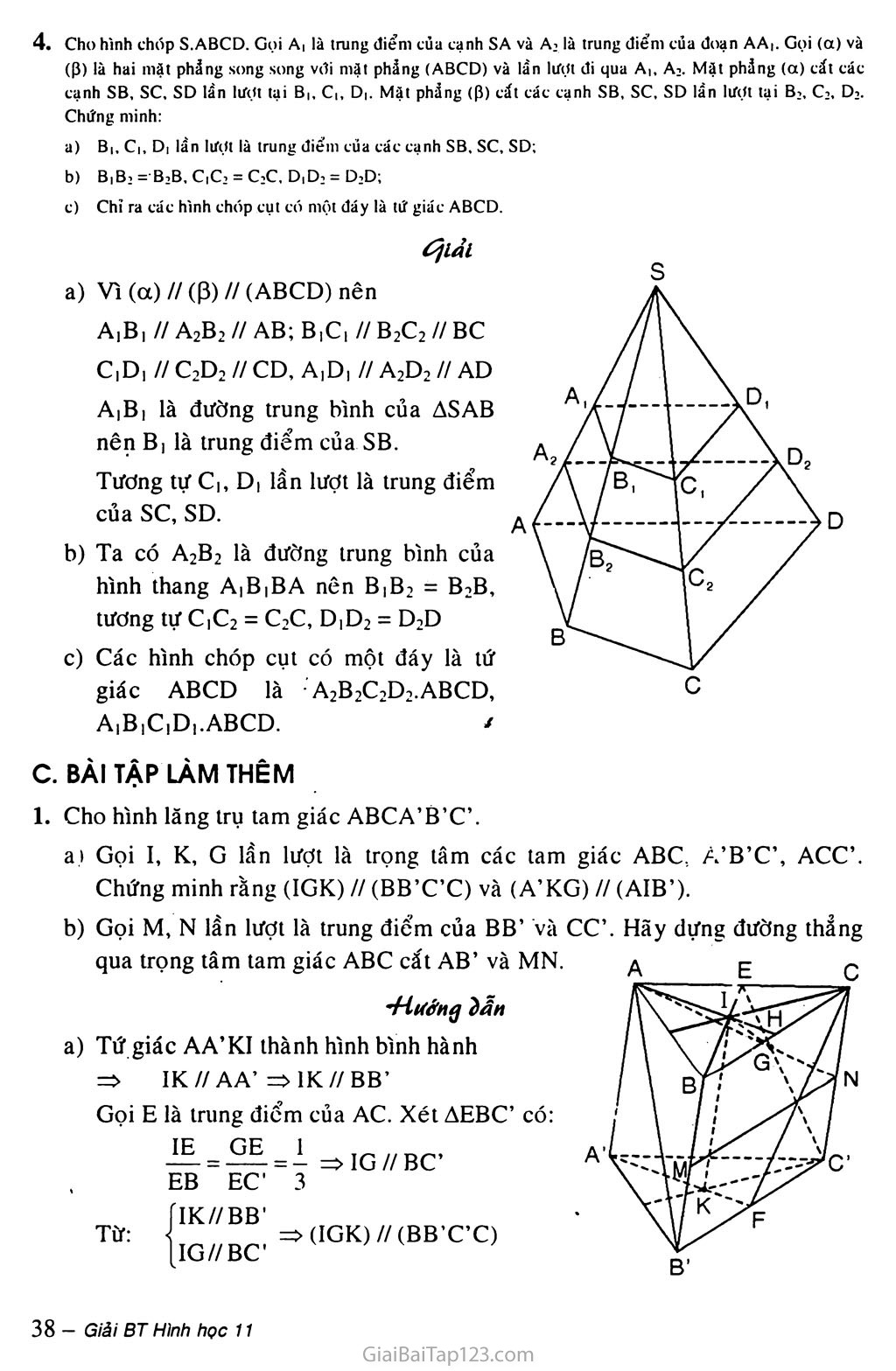
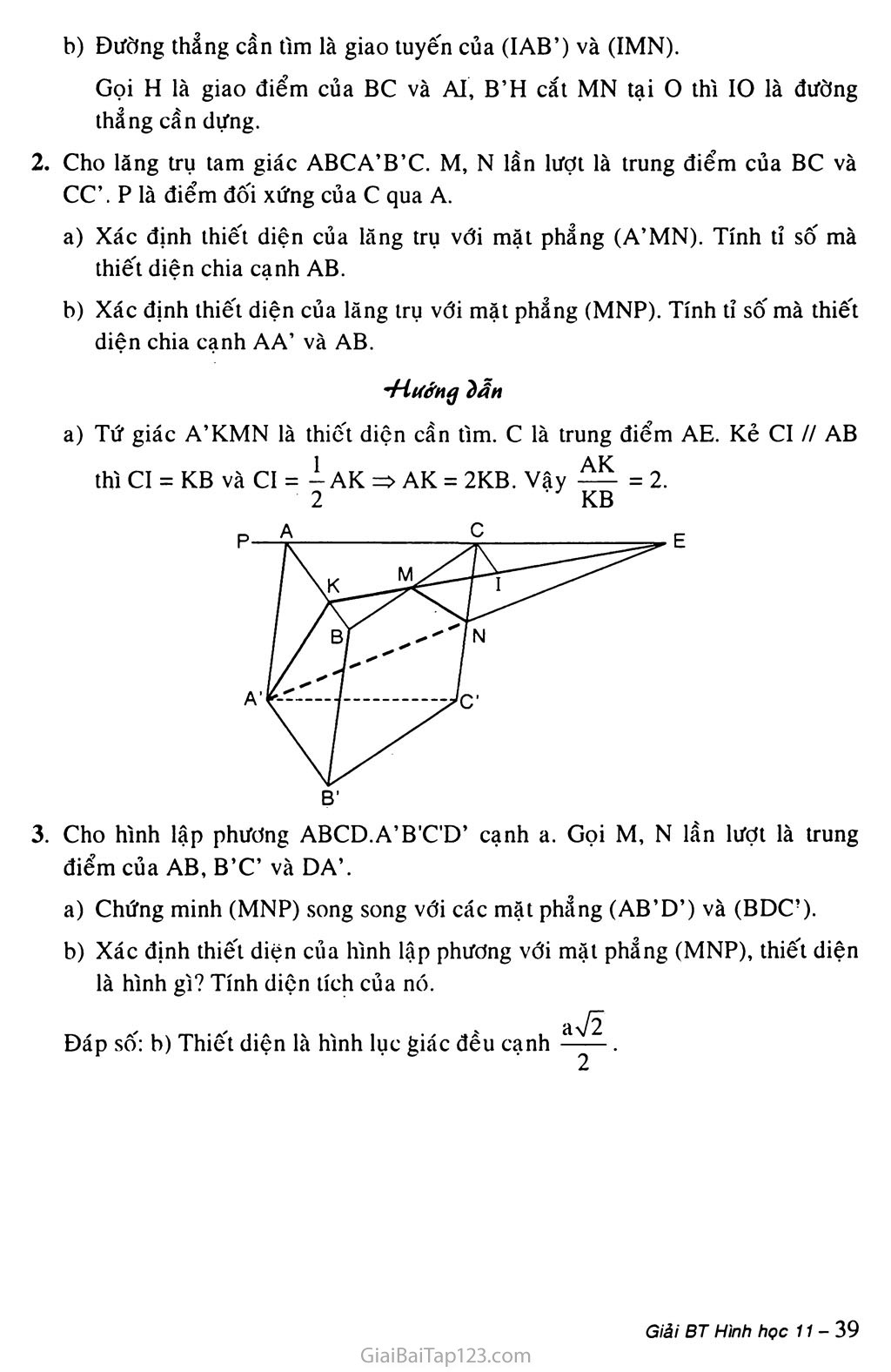
§4. HAI MẶT PHẲNG song song
A. KIẾN THỨC Cơ BẢN
Định nghĩa
Hai mặt phẳng (a), (P) được gọi là song song với nhau nếu chúng không có điểm chung.
Khi đó ta kí hiệu (a) // (P) hay (P) // (a).
Tính chất
Định lí 1: Nếu mặt phẳng (a) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẩng (P) thì (a) song song với (p).
Định lí 2: Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Hệ quả ỉ: Nếu đường thẳng d song song với mặt phẳng (a) thì qua d có duy nhấì một mặt phẳng song song với (a).
/a\	V
Q/
ì/
Á
I b/
V
Hệ qua 2: Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
Hệ quả 3: Cho điểm A không nằm trên mặt phẳng (a). Mọi đường thẳng đi qua A và song song với (a) đều nằm trong một mặt phẳng đi qua A và song song với (a).
Định lí 3: Cho hai mặt phẳng song song với nhau. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Ị>) Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.
dl
ĐịnhlíTa-lét
Định lí 4 (Định lí Ta-lét)
Ba mặt phăng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
Nếu d, d' là hai cát tuyến bất kì cắt ba mặt phẳng song song (a), (P), (y) lần lượt tại các điểm A, B, c và A', B', C' thì AB _ BC _ CA
ATT - B'C'- C'A'
Hình lăng trụ và hình hộp Hình hợp bởi các hình bình hành
AjAjAjA', A2A3A3A2	AnA|AjAn
và hai đa giác AịA2... An và A'A2...A'n gọi là hình lăng ưụ hoặc lãng trụ, và kí hiệu là A.A?...A A'A'...A' .
Nếu đáy của hình lăng ưụ là tam giác, tứ giác, ngũ giác thì lăng trụ tương ứng được gọi là lăng trụ tam giác, lăng ưụ tứ giác, lăng trụ ngũ giác.
Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp. 2
Hình chóp cụt
Cho hình chóp s. A(A2... An; một mặt phẳng (P) không qua đỉnh, song song với mặt phẳng đáy, cắt các cạnh SAị, SA2, ..., SAn lần lượt tại A',
A1,	A'„. Hình tạo bởi thiết diện A'A', ... A'
và đáy AjA9 ... An của hình chóp cùng ỵới các tứ giác A;A'A2A,, A'A'A3A2, ..., A'nA',A,An gọi là hình chóp cụt, kí hiệu A'A^>...A'n.AỊA2...An
A'A'2... A" gọi là đáy nhỏ của hình chóp cụt.
Tính chất:
Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.
Các mặt bên là những hình thang.
Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Trong mặt phẳng (a) cho hình bình hành ABCD. Qua A. B. c. D lần lượt vẽ bốn đường thẳng a, b. c. d song song vđi nhau và không nằm trên (a). Trên a. b, c lần lượt lâ'y ba điểm A', B'. C' tuỳ ý.
Hãy xác định giao điểm D' cùa đường thẳng d vdi mặt phẫng (A'B'C).
Chứng minh A'B’C’D' là hình bình hành.
éịiải
xrT, a // b	_ _
Ta có 	=>(a,AD)//(b,BC)
[AD//BC
Mà (A’B’C’) n (b, BC) = B'C' nên (A'B'C) n (a, AD) = d' đi qua A' song song với B'C’. Gọi D’ là giao điểm của d' với d thì D' = d n (A'B'C').
a//d
Ta có '	=> (a,b)//(c, d).
Vbấ/CD
Ta có: A'D7/B'C'.	(1)
Mặt khác: (a, b) // (c, d) mà (A'B'C'D') n (a, b) = A’B' và (A'B'C'D') n (c, d) = C’D' suy ra A'B' // C'D'.	(2)
Từ (1) và (2) suy ra tứ giác A'B’C'D’ là hình bình hành.
Cho hình lăng trụ tam giác ABC.A B C'. Gọi M và M' lần lượt là (rung điểm của các cạnh BC và B'C'.
Chứng minh rằng AM song song vdi A'M'.
B
Tìm giao điểm của mặt phẩng (AB'C) vói đường thẳng A'M.
Tìm giao tuyến d cùa hai mặt phẵng (AB'C) và (BA'C).
Tìm giao điểm G của đường thẳng d vdi mặt phẩng (AM'M).
Chứng minh G là trọng tâm của tam giác AB'C.
Ta có MM' H BB' và MM' = BB' do đó MM' // AA’ và MM' = AA'.
Suy ra A'M’MA là hình bình hành.
Vậy AM // A'M'.
Gọi I là giao điểm của A'M và AM'.
M'A c (AB'C1) và I € M'A nên I 6 (AB’C).
Vậy I = A’M n (AB’C).
Gọi o là giao điểm của AB’ và A’B.
Ta có: c , o G (AB’C) n (BA’C) => (AB’C) n (BA’C’) = C’O.
Ta có d = C’O c (AB’C) và AM’ c (AB’C').
Gọi G là giao điểm của d và AM’ thì G = d n (AM’M).
Mặt khác OC’ và AM’ là các trung tuyến của AAB’C’ nên G là trọng tâm của AAB'C'.
Cho hình hộp ABCD.A'B'C’D'.
Chứng minh rằng hai mặt phảng (BDA'( và (B'D'C) song song vời nhau.
Chứng minh rằng đưìlng chéo AC' đi qua trọng tâm G| và G] của hai tam giác BDA' và B'D'C.
Chứng minh Ũ! và Ơ! chia đoạn AC' thành ba phần bằng nhau.
Gọi o và I lần lượt là tâm cùa các hình bính hành ABCD và AA'C'C. Xác định thiết diện của.mặt phẵng (A' 10) vói hình hộp đã cho.
Ốịlảí
Chứng minh (BDA')//(B’D’C)
Ta có tứ giác BB’D’D và A’B’CD là các hình bình hành nên: BD // B’D’ và AD’//B'C => hai mặt phẳng (BDA’) và (B’D’C) có các cặp đường thẳng cắt nhau và song song nhau từng đôi một nên chúng song song. Vậy (BDA’)//(B’D’C).
Chứng minh G|, Gs e AC’
Gọi o, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’.
OA
AG,
G| là trọng tâm AA'BD.
Trong mặt phẳng (AA’C’C) gọi G|, G2 lần lượt là giao điểm của AC’ với A’O và O’C. Ta chứng minh G|, Gs lần lượt là trọng tâm của AA’BD và ACB’D’. Thật vậy, ta có AG|OA co AG|A’C’ (vì AC // A’C’).
G,A'
A'C' 2 A'O 2
Tương tự Gs là trọng tâm của ACB’D’ Vậy AC’ đi qua G|, Gs.
Chứng minh AG| = GịGs = GịC’
AG, AO 1
Theo câu trên ta có:
G,C'
A'C'
AG| = - AC’ 3
Tương tự:
C'G2
g2a
2- (vì AGịOA co AG]A’C’) 2 (1)
C’G2= ỵAC’ (2)
3
= (viAGsC’O’ co AGsAC) CA 2 1
Từ (1) và (2) suy ra AG| = G|Gs = GsC’.
(A'IO) = (Ỉ\.KQ'C} =>(A'IO) cắt hình hộp đã cho theo thiết diện là hình
bình hành AA'C'C.
Cho hình chóp S.ABCD. Gọi A| là trung điểm của cạnh SA và A2 là trung điểm của đoạn AA|. Gọi (a) và
(P) là hai mặt phảng song song vđi mát phẵng (ABCD) và lần lượt đi qua A|. A2. Mặt phẳng (a) cắt các cạnh SB, sc, SD lẩn lượt tại B|, C|, D|. Mặt phăng (P) cát các cạnh SB, sc, SD lần lượt tại B2, c2, Dị. Chứng minh:
B|, Ci, D| lần lượt là trung điểm của các cạnh SB. sc, SD;
B,B2 = B2B,C|C2 = C2C, D,D2 = D2D;
Chi ra các hình chóp cụt có một đáy là tứ giác ABCD.
Ốịíảl
Vì (a) // (3) // (ABCD) nên A,B, // A2B2 // AB; B|C| // B2C2 // BC C|D| // C2D2 // CD, A|D, // A2D2 // AD AịB, là đường trung bình của ASAB nên B| là trung điểm của SB.
Tương tự C|, D| lần lượt là trung điểm của SC, SD.
Ta có A2B2 là đường trung bình của hình thang AịB|BA nên B|B2 = B2B, tương tự C]C2 = C2C, d,d2 = D2D
Các hình chóp cụt có một đáy là tứ giác ABCD là A2B2C2D2.ABCD,
A| B |C|D|. ABCD.	t
c. BÀI TẬP LÀM THÊM
Cho hình lăng trụ tam giác ABCA’B’C’.
ai Gọi I, K, G lần lượt là trọng tâm các tam giác ABC, A’B’C’, ACC’. Chứng minh rằng (IGK) // (BB’C’C) và (A’KG) // (AIB’)'
b) Gọi M, N lần lượt là trung điểm của BB’ và CC’. Hãy dựng đường thẳng qua trọng tâm tam giác ABC cắt AB’ và MN.
•Hưởng ỉẫn
a) Tứ giác AA’K.1 thành hình bình hành => IK//AA’ =>1K//BB’
Gọi E là trung điểm của AC. Xét AEBC’ có:
IG // BC’
IE _ GE _ 1
,	EB EC 3
Từ:
(IGK)//(BB’C’C)
IG//BC’
ÍIK//BB’
b) Đường thẳng cần tìm là giao tuyến của (IAB’) và (IMN).
Gọi H là giao điểm của BC và AI, B’H cắt MN tại o thì 10 là đường thẳng cần dựng.
Cho lăng trụ tam giác ABCA’B’C. M, N lần lượt là trung điểm của BC và CC’. p là điểm đối xứng của c qua A.
a) Xác định thiết diện của lăng trụ với mặt phẳng (A’MN). Tính tỉ số mà thiết diện chia cạnh AB.
b) Xác định thiết diện của lăng trụ với mặt phẳng (MNP). Tính tỉ số’ mà thiết diện chia cạnh AA’ và AB.
-Hướng ĩ)ẫn
a) Tứ giác A’KMN là thiết diện cần tìm. c là trung điểm AE. Kẻ CI // AB
Cho hình lập phương ABCD.A’B'C'D’ cạnh a. Gọi M, N lần lượt là trung điểm của AB, B’C’ và DA’.
■ a) Chứng minh (MNP) song song với các mặt phẳng (AB’D’) và (BDC!).
b) Xác định thiết diện của hình lập phương với mặt phẳng (MNP), thiết diện là hình gì? Tính diện tích của nó.
Đáp số: b) Thiết diện là hình lục giác đều cạnh