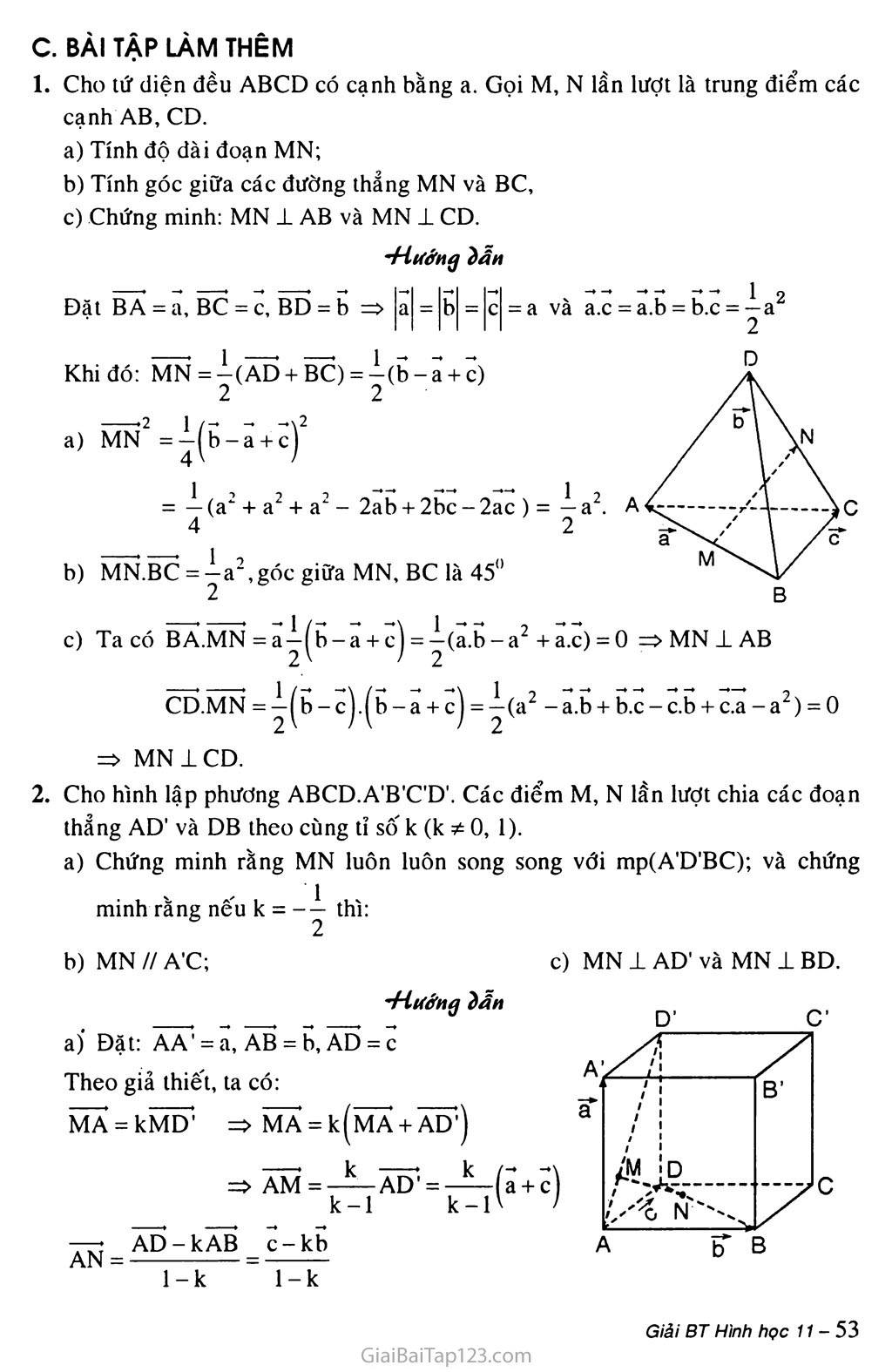
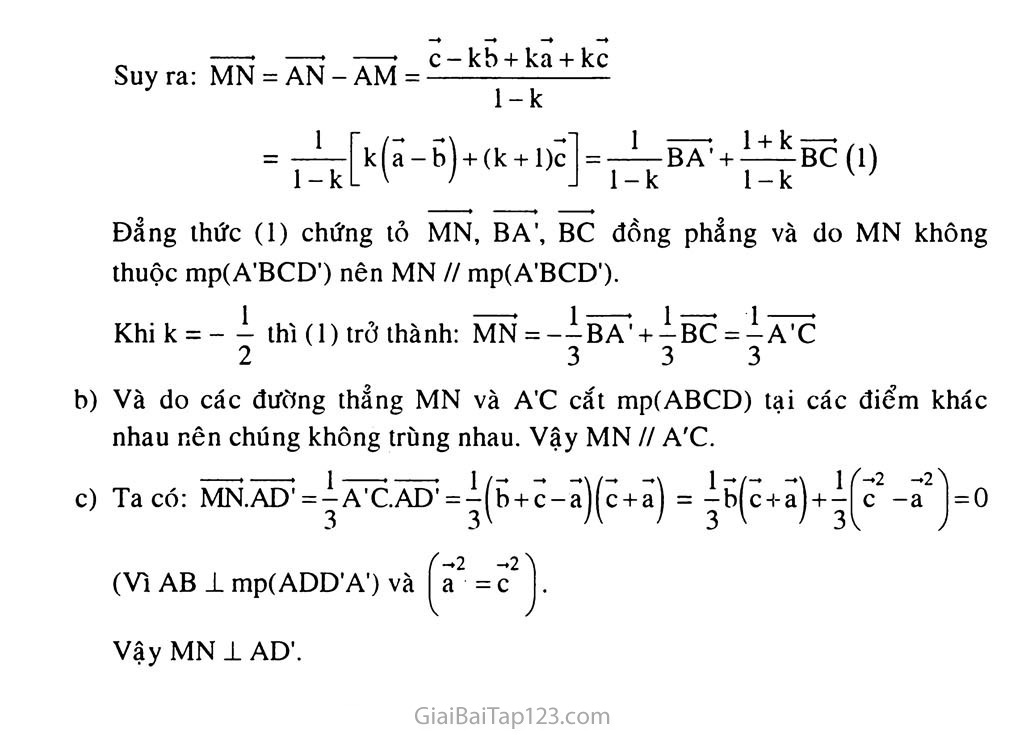Giải toán 11 Bài 2. Hai đường thẳng vuông góc
§2. HAI ĐƯỜNG THẲNG VUÔNG GÓC A. KIẾN THỨC Cơ BẢN Tích vô hướng của hai vectơ trong không gian Góc giữa hai vectơ trong không gian ĐỊnlì nglĩĩa: Trong không gian, cho u và V là hai vectơ khác vectơ-không. Lấy một điểm A bất kì, gọi B và c là hai điểm sao cho AB = U, AC = V. Khi đó ta gọi góc BAC (0" < BAC <180") là góc giữa hai vectơ ũ và V trong không gian, kí hiệu là (U , V) u Tích vô hướng của hai vectơ trong không gian Địnlì nghĩa: Trong không gian cho hai vectơ U và V đều khác vectơ -không. Tích vô hướng của hai vectơ U và V là một số, kí hiệu là U.V, đưực xác định bởi công thức: U.v = |u|.|v|.cos(u,v) Vectơ chỉ phương của đường thẳng Định nghĩa: Vectơ ã khác vectơ - không được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ ẩ song song hoặc trùng với đường thẳng d. Góc giữa hai đường thẳng trong không gian Định nghĩa: Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a' và b' cùng đi qua một điểm và lần lượt song song với a và b. Hai đường thẳng vuông góc Định nghĩa: Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°. Kí hiệu hai đường thẳng a và b vuông góc với nhau là a ± b. B. PHƯƠNG PHÁP GIẢI BÀI TẬP c) AB và DH. Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp veclơ sau đây a) AB và EG ; b) ÃẼ và EG ; éịiải a) Ta có EG = AC nên (AB, ẼG) = (ÃB,Ãc) = 45°. Tam giác FAC đều nên (ÃF, ẼG) = (ÃF,Ãc)=60°. (ÃB, DH)-(ÃB + Ăe) = 90°. Cho tứ diện ABCD. Chứng minh rằng AB.CD + AC.DB + AD.BC = 0. Từ đáng thức trên hãy suy ra rằng nếu tứ diện ABCD có AB _L CD và AC J. DB thi AD jL BC. éjiải a) Ta có AB.CD + AC.DB + AD.BC = ÃB(ÃD -ÃC) + Ãc(ÃB - Ãd) + Ãd(ÃC - Ãb) = AB.AD - AB.AC + AC.AB. - AC.AD + AD.AC - AD.AB = 0 b) Nếu AB 1 CD và AC 1 BD thì AB.CD = 0 và AC.DB = 0. Theo câu a) suy ra AD.BC = 0 =>AD±BC. a) Trong không gian nếu hai đường Ihẳng a và b tùng vuông góc với dưìlng [hẵng c thi a và b có song song vời nhau không? b) Trong không gian nếu đường thẩng a vuông góc vôi đường thẳng b và đưilng thăng b vuông góc với đưìtng thẳng c thì a có vuông gót với c không ? Lời a và b nói chung không song song a và c nói chung không vuông góc. Trong không gian cho hai lam giác đều ABC và ABC’ có chung cạnh AB và nằm trong hai mặt phầng khác nhau. Gọi M. N. p. Q lần lượt là trung điểm của các cạnh AC, CB. BC. C’A. Chứng minh rằng: AB ICC'; Tứ giác MNPQ là hình chữ nhật. => MQ // NP và MQ = NP => MNPQ là hình bình hành. Mặt khác PQ // AB, MQ // cc, AB 1 CC' nên MQ 1 PQ. Do đó hình bình hành MNPQ là hình chữ nhật. Cho hình chóp tam giác S.ABC có SA = SB = sc và có ASB = BSC = CSA. Chứng minh ràng SA -L BC, SB 1 AC, SC 1 AB.. Ốjiải Ta có SA.BC = SA.(SC - SB) = SA.SC - SA.SB = SA.SC.cosASC - SA.SB.cosASB = 0 => SA 1 BC Chứng minh tương tự ta đưực SB 1 AC, sc 1 AB. Trong không gian cho hai hình vuông ABCO và ABC’D' có chung cạnh AB và nằm trong hai mặt phẫng khác nhau, lần lượt có tâm o và O'. Chứng minh rằng AB 1 OO’ và tứ giác CDD'C là hình chữ nhật. ốỊiải Ta có ÃB.ÕÕ' = ÃB.(ÃƠ - Ãõ) = ÃB.ÃỠ - ÃB.ÃÕ D = AB.AO'cos45" - AB.AO.cos45° = 0 => AB 1 OO'. Ta có CD // C'D' và CD = CD' nên tứ giác CDD'C là hình hình hành. Mặt khác OO' // CC' nên CC' 1 AB => CC' 1 CD. Vậy hình bình hành CDDC' là hình chữ nhật. Cho s là diện lích của lam giác ABC. Chứng minh rằng: s = Jab”. AC’ -(AB.AC)". Ốịlảl Vì cosA = AB.AC IãbI.IăcI nên v/r cos2 A = I AB2 .AC2 -(AB.AC)2 —.2 —.2 AB .AC Ta có SABC =^AB.ACsin A = 4aB.AcVi - cos2 A. Do đó SABC =|ỰaB2.AC2 - (AB.AC)2. Cho tứ diện ABCD có AB = AC = AD và BAC = BAD = 60". Chứng minh rằng: AB 1 CD; Nếu M, N lần lượt là trung điểm cùa AB và CD thì MN _L AB và MN _L CD. úịiàl AB.CD =ÃB.(ÃD - ÃC) = ÃB.ÃD - ÃB.ÃC = AB.AD.cosóO" - AB.AC.cosóO0 = 0 => AB 1 CD. MN = |(AD + BC)-|(AD + AC-AB) (bài tập 4) => AB.MN =ị(ÃB.ĂD + ÃB.ÃC-ÃB2) 2 = |(AB2 cos60° + AB2 cos60° - AB2) = 0 Do đó MN 1 AB. Chứng minh tương tự ta có m/ / X / X / X / X / X / \ / ' X \ X \ 0 \ \ > X s^ X s' X s' X s' X y' X s' /N CD.MN = j(ÃD - ÃC).(ÃD + AC - ÃẼ Vậy MN 1 CD. BÀI TẬP LÀM THÊM Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm các cạnh AB, CD. Tính độ dài đoạn MN; Tính góc giữa các đường thẳng MN và BC, Chứng minh: MN 1 AB và MN 1 CD. -Hưártỹ iẫn Đặt BA = a, BC = c, BD = b => |a| = |b| = |c| = a và a.c = a.b = b.c = ^-a2 c) Ta có BA.MN =a^b-a + cj = ^-(a.b-a2 + a.c) = 0 => MN ± AB CD.MN = y(b-c).(b-a + c) = y(a2 -a.b + b.c-c.b + c.a-a2) = 0 =} MN1CD. Cho hình lập phương ABCD.A'B'C'D'. Các điểm M, N lần lượt chia các đoạn thẳng AD' và DB theo cùng tỉ số k (k 0, 1). Chứng minh rằng MN luôn luôn song song với mp(A'D'BC); và chứng minh rằng nếu k = " thì: MN // A'C; c) MN 1 AD' và MN 1BD. D’ C’ A r B 'Hướng ỉẫn aj Đặt: AA' = a, AB = b, AD = C Theo giả thiết, ta có: MA = kMD' MA = k(MA + AD') => ÃM = ~ÃẼT=-^-ía+c k-1 k-n —; AD-kAB c-kb 1-k 1-k Suy ra: MN = AN - AM = —77 c-kb + ka + kc AM = — 1-k 1-k k(a-b) + (k + l)c — BA' + ^^BC(l) -k 1-k v 7 1-k Đẳng thức (1) chứng tỏ MN, BA', BC đồng phẳng và do MN không thuộc mp(A'BCD') nên MN // mp(A'BCD'). Khik = - ị thì (1) trở thành: MN = -^BA^ + ^BC = Ịã7C 2 3 3 3 Và do các đường thẳng MN và A'C cắt mp(ABCD) tại các điểm khác nhau nên chúng không trùng nhau. Vậy MN // A'C. Ta có: MN.AD' = “A'C.AD' =-j(b + c-a)(c + a) =-^b^c+aj+^c -a ^ = 0 (Vì AB ± mp(ADD'A') và ^a = c y Vậy MN 1 AD'.