Giải toán 11 Bài 3. Đường thẳng vuông góc với mặt phẳng

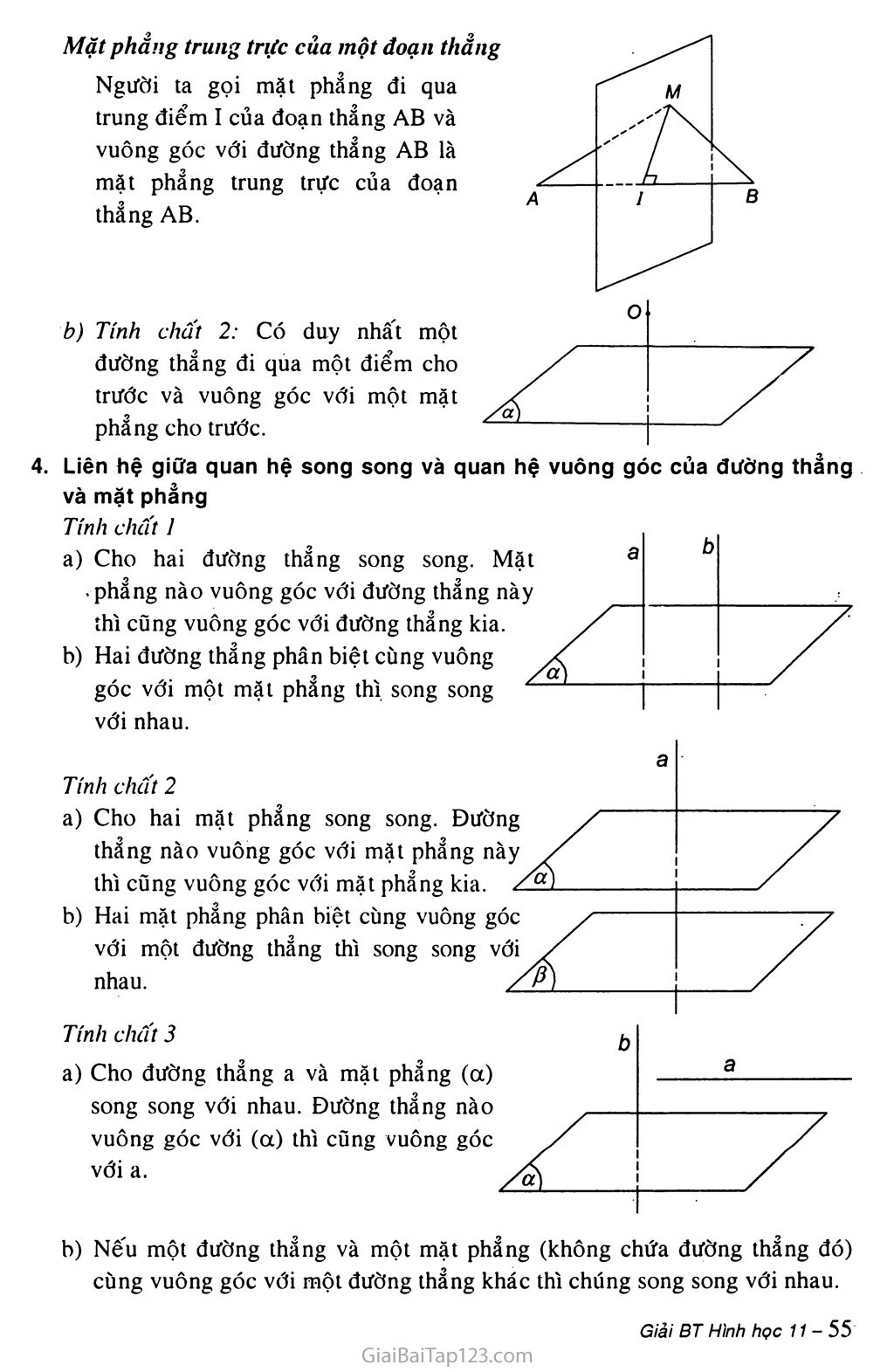
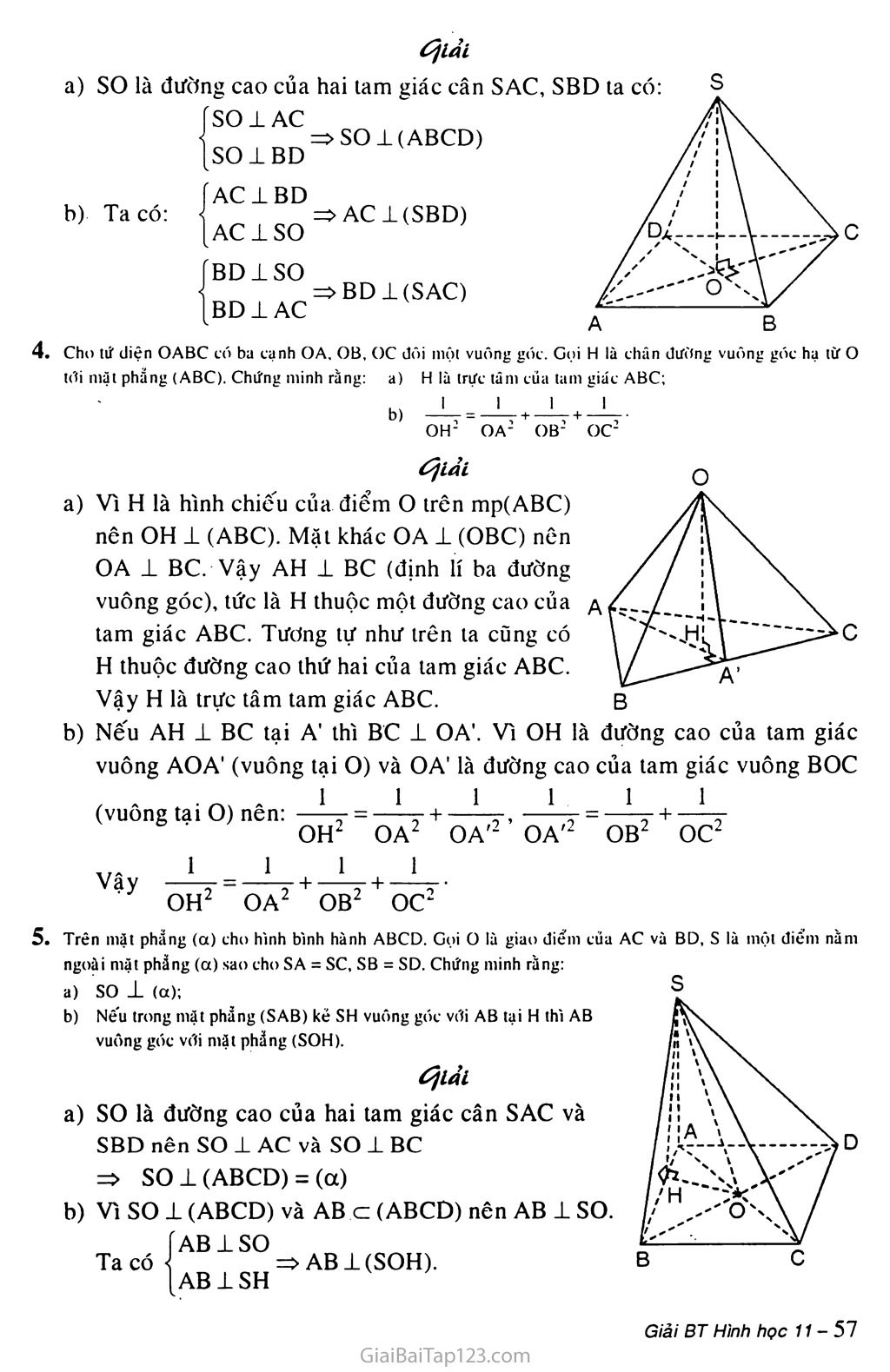
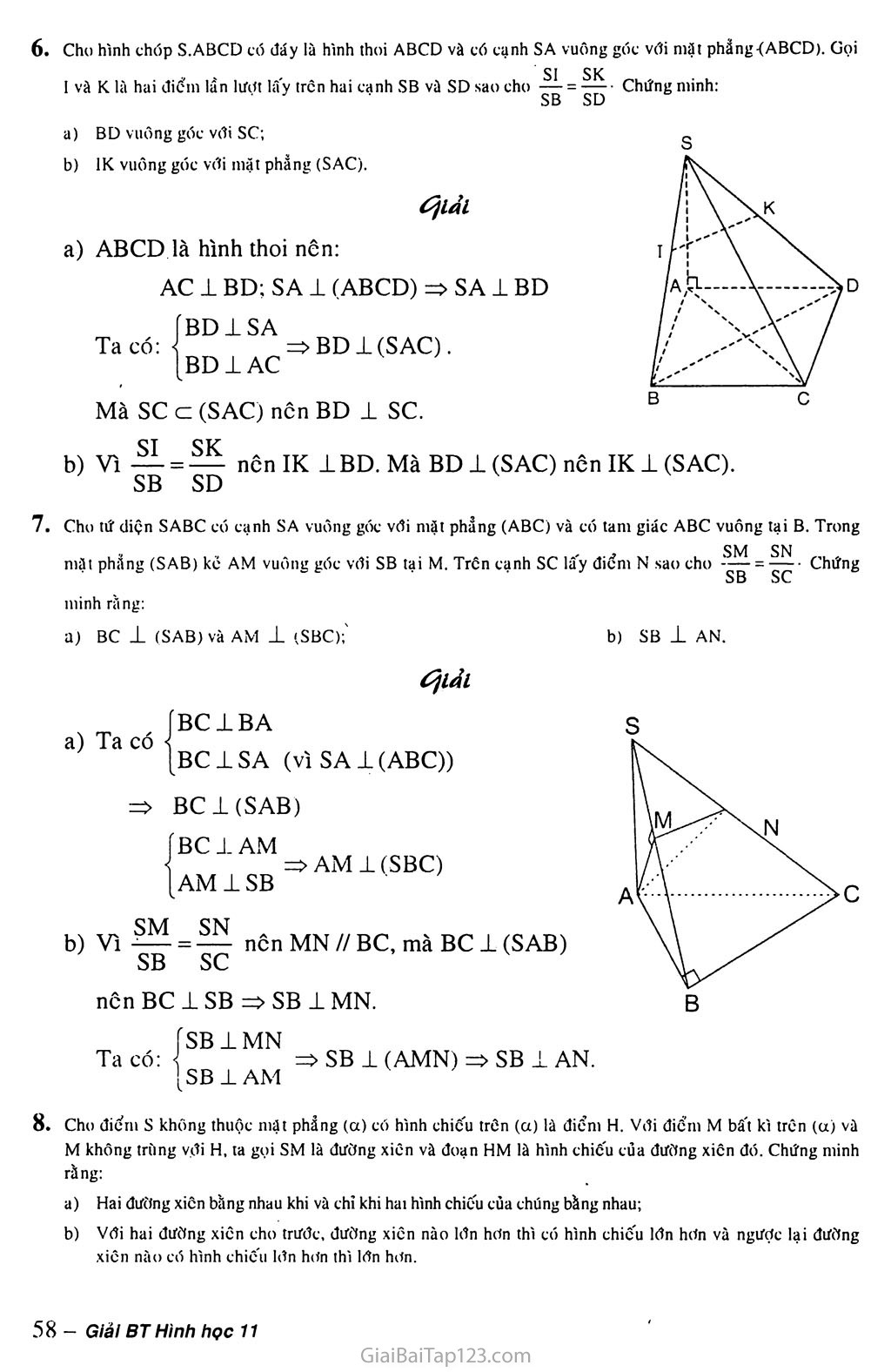
§3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHANG
A. KIẾN THỨC Cơ BẢN
Định nghĩa
Đường thẳng d được gọi là vuông góc với mặt phẩng (a) nếu d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (a).
Kí hiệu là d 1 (a).	/
Điều kiện để đường thẳng vuông góc với mặt phẳng
Định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì
nó cũng vuông góc với cạnh thứ ba của tam giác đó.
rinh châ't
d
a) Tính chất I: Có duy nhát một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
M
■-r
\
A
1
B
Mặt phẳng trung trực của một đoạn thẳng Người ta gọi mặt phẳng đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng AB là mặt phẳng trung trực của đoạn thẳng AB.
Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
Tính chất ì
Cho hai đường thẳng song song. Mặt • phẳng nào vuông góc với đường thẳng này
thì cũng vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
7Yn/ỉ chất 2
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.	/p
b
a
/a}
/
/
/
Tính chất 3 a) Cho đường thẳng a và mặt phẳng (a) song song với nhau. Đường thẳng nào vuông góc với (a) thì cũng vuông góc với a.
b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó)
cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
Định lí ba đường vuông góc
b ± a b 1 a'
Định nghĩa: Phép chiếu song song lên mặt phăng (P) theo phương 1 vuông góc tới mặt phẳng (P) gọi là phép chiếu vuông góc lên mặt phẳng (P).	Q
Định lí (Định lí 3 đường vuông góc)
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). Khi đó điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a' của a trên (P).
Góc giữa đường thẳng và mặt phẳng
Định nghĩa: Nếu đường thẳng a ± (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 90°.
Nếu đường thẳng a không vuông góc với mặt phẳng (P)
(a) thì góc giữa a và hình chiếu a' của nó trên (P) gọi là góc giữa đường thẳng a và mặt phẳng (P).
Chú ý: Nếu (p là góc giữa đường thẳng d và mặt phẳng (a) thì ta luôn có 0° < tp < 90°.
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Cho hai dường thẳng phân biệt a, b và mặt phẵng (a). Các mệnh đề sau đây đúng hay sai?
a) Nếu a // (a) và b J_ (a) thì a _L b.	b) Nếu a // (a) và b -L a thì b _L (a).
Nếu a // (a) và b // (a) thí b // a.	d) Nếu a _L (a) và b -L a thì b // (a).
Đúng; b) Sai; c) Sai; d) Sai.
Cho tứ diện ABCD có hai mạt ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi 1 là trung điểm cùa cạnh BC.
Chứng minh rằng BC vuông góc vời mặt phẵng (ADI).
Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc vdi mặt phẫng (BCD).
ốỊiải
Tam giác ABC và BCD cân có đáy BC và I là trung điểm của BC nên
AI 1 BC
' 7:7 =>BC1(ADI)
DI 1 BC
Ta có BC 1 (ADI) và AH c (ADI)
=> AB ± AH
AHl(BCD)
AH1DI
ÍAH1BC
Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có SA = SB = sc = SD. Gọi o là giao điểm của AC và BD. Chứng minh rằng:
Đường thăng so vuông góc với mặt phẩng (ABCD).
Đường thẳng AC vuông góc vdi mat phẳng (SBD) và đưítng thẳng BD vuông góc vói mạt phảng (SAC).
ốịiải
b) Ta có:
ACl(SBD)
a) SO là đường cao của hai tam giác cân SAC, SBD ta có: ÍSO1AC
SOl(ABCD)
BD1 (S AC)	
A	B
Cho tứ diện OABC có ba cạnh OA, OB, oc dõi một vuông góc. Gụi H là chân dường vuông góc hạ từ o tdi mặt phăng (ABC). Chứng ntinh rằng: a) H là trực tâm của tam giác ABC;
b)
OB2 oc2
1111
OH2 OA2
ốỊiải
Vì H là hình chiếu của điểm o trên mp(ABC) nên OH 1 (ABC). Mặt khác OA 1 (OBC) nên OA 1 BC. Vậy AH 1 BC (định lí ba đường vuông góc), tức là H thuộc một đường cao của tam giác ABC. Tương tự như trên ta cũng có H thuộc đường cao thứ hai của tam giác ABC.
Vậy H là trực tâm tam giác ABC.
Nếu AH 1 BC tại A' thì BC 1 OA’. Vì OH là đường cao của tam giác vuông AOA’ (vuông tại 0) và OA' là đường cao của tam giác vuông BOC
(vuông tại O) nên:
1 1
OH
2 OA2 + OA'2 ’ OA'2 OB2 + oc2
Vậy
111111
OH2 OA2 OB2 oc2
Trên mặt phẵng (a) cho hình bình hành ABCD. Gọi o là giao điểm của AC và BD, s là một điểm nằm ngoài mặt phẳng (a) sao cho SA = sc, SB = SD. Chứng minh răng:
SO 1 (a);
Nếu trong mặt phẵng (SAB) kẻ SH vuông góc vời AB tại H thì AB vuông góc với mặt phẳng (SOH).
Ốjíải
SO là đường cao của hai tam giác cân SAC và SBD nên so 1 AC và SO 1 BC => SO 1 (ABCD) = (a)
Vì SO 1 (ABCD) và AB c (ABCD) nên AB 1 so.
ÍAB1S0 _ ,
Ta có (	=>AB±(SOH).
I AB 1SH
6. Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phắng-(ABCD). Gọi SI SK
1 và K là hai điổin lần lượt lâ'y tròn hai cạnh SB và SD sao cho -77 = 7— • Chứng minh:
SB Sũ
BD vuông góc vơi SC;
1K vuông góc vói mặt phẳng (SAC).
íỹ.ải
ABCD là hình thoi nên:
AC 1 BD; SA 1 (ABCD) => SA 1 BD
BD1SA BD1 AC
Ta có:
> BD 1 (SAC)
Mà SC c (SAC) nôn BD 1 sc.
Vì H; = UI ncn IK 1BD. Mà BD 1 (SAC) nên IK 1 (SAC). •
SB SD
7. Cho tứ diện SABC có cạnh SA vuông góc vđi mặt phẳng (ABC) và có tam giác ABC vuông tại B. Trong
ntặt phẵng (SAB) kẻ AM vuông góc với SB tại M. Trôn cạnh sc lấy điểm N sao cho = -|^7 ■ Chứng SB sc
minh rằng:
a) BC ± (SAB) và AM ± (SBC);'
tfiải
[BC1BA
[bCISA (vì SAI (ABC))
b) SB ± AN.
a) Ta có
=> BCl(SAB)
f BC 1 AM
AM 1 SB
■AMI (SBC)
b) Vì IU = m ncn MN // BC, mà BC 1 (SAB) SB sc
ncn BC 1 SB => SB 1 MN
ÍSB1MN
Ta có:
SB ± AM
SB 1 (AMN) => SB 1 AN.
8. Cho điếm s không thuộc mạt phẳng (a) có hình chiếu trổn (a) là điểm H. vơi điểm M bâ't kì trên (u) và M không trùng v.ơi H, ta gọi SM là đường xiên và đoạn HM là hình chiếu cùa đường xicn đó. Chứng minh ràng:
Hai đường xiên bằng nhau khi và chì khi hai hình chiếu cùa chúng băng nhau;
Vời hai đường xiên cho trưđc, đường xicn nào lớn hdn thì có hình chiếu lơn hơn và ngược lại đường xiên nào có hình chiếu ldn hơn thì lơn hơn.
ỐỊiắi
Giả sử HM, HN lần lượt là hình chiếu của SM, SN.
Nếu SM = SN thì ASHM = ASHN nên HM = HN
Ngược lại nếu HM = HN thì ASHM = ASHN nên SM = SN Vậy SM = SN HM = HN
Áp dụng định Py-ta-go ta có:
SM2 - HM2 = SN2 - HN2 (= SH2)
=>SM2-SN2 = HM2-HN2.
Từ đó suy ra: SM > SN HM > HN (đpcm).
c. BÀI TẬP LÀM THÊM
Cho tứ diện ABCD.
Chứng minh rằng AB 1 CD AC2 - AD2 = BC2 - BD2.
Từ đó suy ra nếu một tứ diện có hai cặp cạnh đối vuông góc với nhau thì cặp cạnh đối còn lại cũng vuông góc với nhau.
Cho tứ diện SABC có ABC là tam giác vuông cân đỉnh B, AB = a, SA vuông góc với mặt phẳng (ABC) và SA - a 73. M là điểm tùy ý trên cạnh AB, đặt AM = X (0 < X < a). Gọi (a) là mặt phẳng qua M và vuông góc với AB.
Tìm thiết diện của tứ diện SABC với (a).
Tính diện tích thiết diện này theo a và X. Tìm X để diện tích thiết diện có giá trị lớn nhá t.
Đáp số: b) s = 73 X (a - x), s lớn nhất khi X = 4.
2
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA ± (ABCD) và SA = a.
Tìm trên mặt phẳng (ABCD) một điểm cách đều ba điểm s, B, c và tính khoảng cách từ điểm đó đến mặt phẳng (SBC).
Tìm trên mặt phẳng (SBC) một điểm cách đều ba điểm B, c, M với M là trung điểm cạnh CD. Tính khoảng cách chung ấy.
Đáp số: a) Trung điểm N của cạnh AD và có độ dài SN = BN = CN =
b)
ì 76