Giải toán 11 Bài 4. Hai mặt phẳng vuông góc
4. HAI MẶT PHẲNG VUÔNG GÓC
A. KIẾN THỨC Cơ BẢN
Góc giữa hai mặt phẳng
Định lí: Gọi s là diện tích của đa giác H trong mặt phẳng (P) và S' là diện tích hình chiếu H' của H trên mặt phẳng (P’) thì S' = s costp, trong đó ọ là góc giữa hai mặtphẳng (P) và (P').
Hai mặt phẳng vuông góc
Định nghĩa: Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng 90". Kí hiệu (P) _L (Q).
Định lí (Điều kiện đế hai mặt plĩẳng vuông gác)
Nêu một mặt phẳng chứa một đường thẳng vuông góc với một
Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phăng đó.
■(P)l(Q)
mặt phắng khác thì hai mặt phắng đó vuông góc với nhau. íac(P).
[a±(Q):
Định lí: Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng (P), vuông góc với giao tuyến của (P) và (Q) đều vuông góc với mặt phẳng (Q).
(p)n(ọ) = d; (P)±(Q)
al(Q)
a ±d
Hệ quả 1: Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau và A là một điểm nằm tron; nằm trong (P).
(P)l(Q)
■ac(P)
Ae(P)
al(Q)
Aea
Hệ qua 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao luyến của chúng vuông góc với mặt phẳng thứ ba.
(P)n(Q) = a
(P) -L(R)
(Q) l(R)
• a 1 (R)
r- - <§]
Hệ ÌỊUCÍ 3: Qua đường thẳng a không vuông góc với mặt phẳng (P) có duy nhát một mặt phẳng (Q) vuông góc với mặt phẳng (P).
Hình lãng trụ đứng, hình hộp chữ nhật, hình lập phương
Định nghĩa:
Hình lănị’ trụ đứnị’:
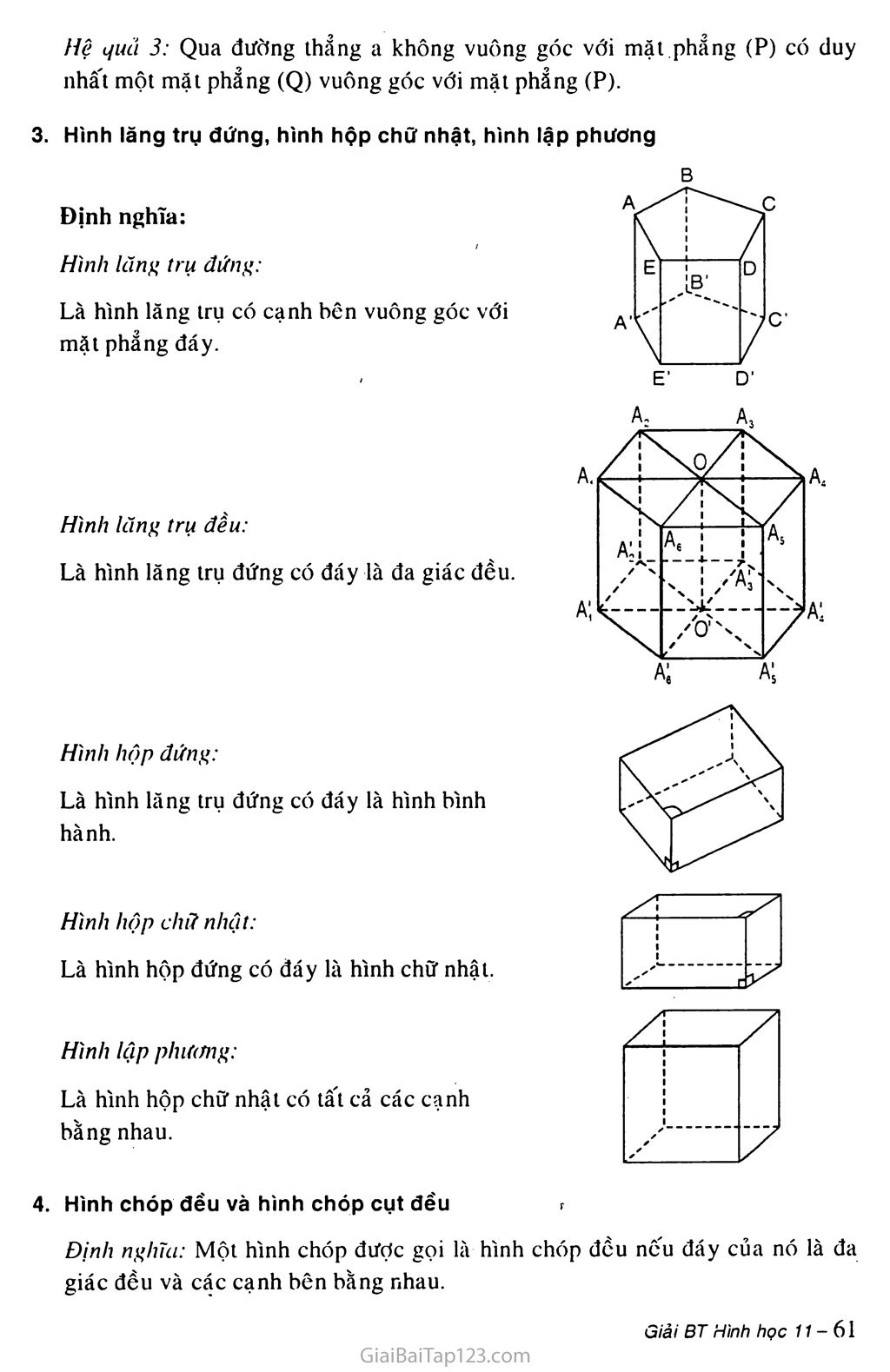
Là hình lăng trụ có cạnh bên vuông góc với mặt phẳng đáy.
Hình lănịỊ trụ đều:
Là hình lăng trụ đứng có đáy là đa giác đều
Hình hộp đứnịỊ:
Là hình lăng trụ đứng có đáy là hình bình hành.
Hình hộp chữ nhật:
Là hình hộp đứng có đáy là hình chữ nhật.
Hình lập phương:
Là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
Hình chóp đều và hình chóp cụt đều
B
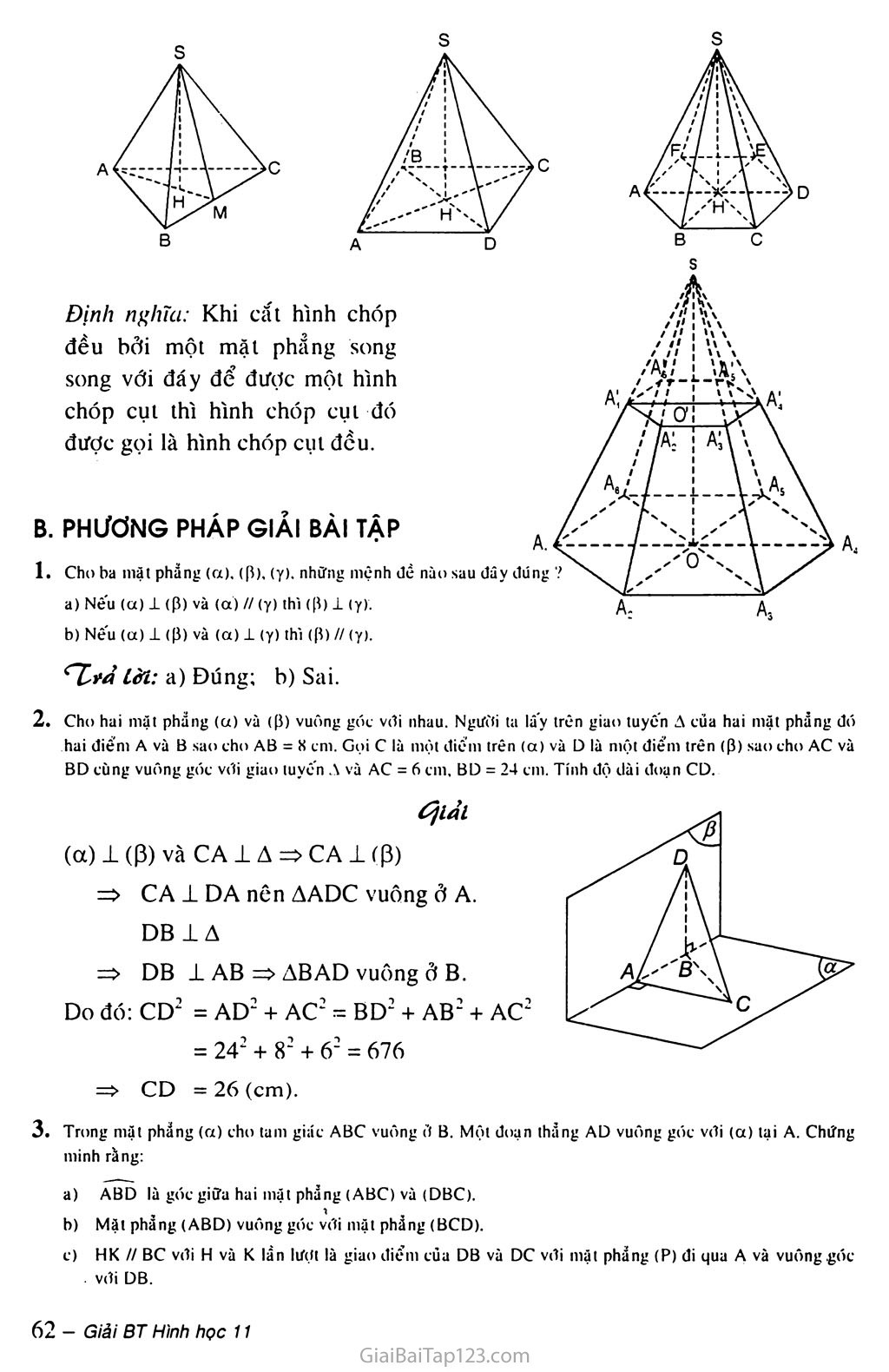
Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau.
->D
Định nghĩa: Khi cắt hình chóp
đều bởi một mặt phẳng song
song với đáy để được một hình
chóp cụt thì hình chóp cụt đó
được gọi là hình chóp cụt đều.
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Cho ba mặt phẩng («), (p), (y). những mệnh đề nào sau I
Nếu (a) 1 (p) và (có // (y) thi (P) ± (y).
Nếu (a) 1 (P) và (a) 1 (y) thì (p) // (y).
("Cm Lời: a) Đúng; b) Sai.
Cho hai mật phung (ơ) và (P) vuông góc vói nhau. Người ta lấy trên giao tuyến A của hai mặt phẫng đó
hai điểm A và B sao cho AB = s cm. Gọi c là một điểm trên (a) và D là một điểm trên (P) sao cho AC và
BD cùng vuông góc với giao tuyên A và AC = 6 cm, BD = 24 cm. Tính độ tlài đoạn CD.
Ốịiẳl
(a) 1 (p) và CA 1 A => CA 1 íp)
=> CA 1 DA nên AADC vuông ở A.
DB 1 A
=> DB ± AB => ABAD vuông ở B.
Do đó: CD2 = AD2 + AC2 = BD2 + AB2 + AC2
= 242 + 82 + 62 = 676
=> CD = 26 (cm).
Trong mặt phẳng (ct) cho tam giác ABC vuông ("I B. Một đoạn thẳng AD vuông góc với (a) tại A. Chứng
minh rằng:
ABD là góc giữa hai mật phẵng (ABC) và (DBC).
Mặt phẳng (ABD) vuông góc vời mặt phăng (BCD).
HK // BC vđi H và K lần lượt là giao điểm của DB và DC vói mặt phẳng (P) đi qua A và vuông góc
vời DB.
A,
A.
A-,
ỐỊiải
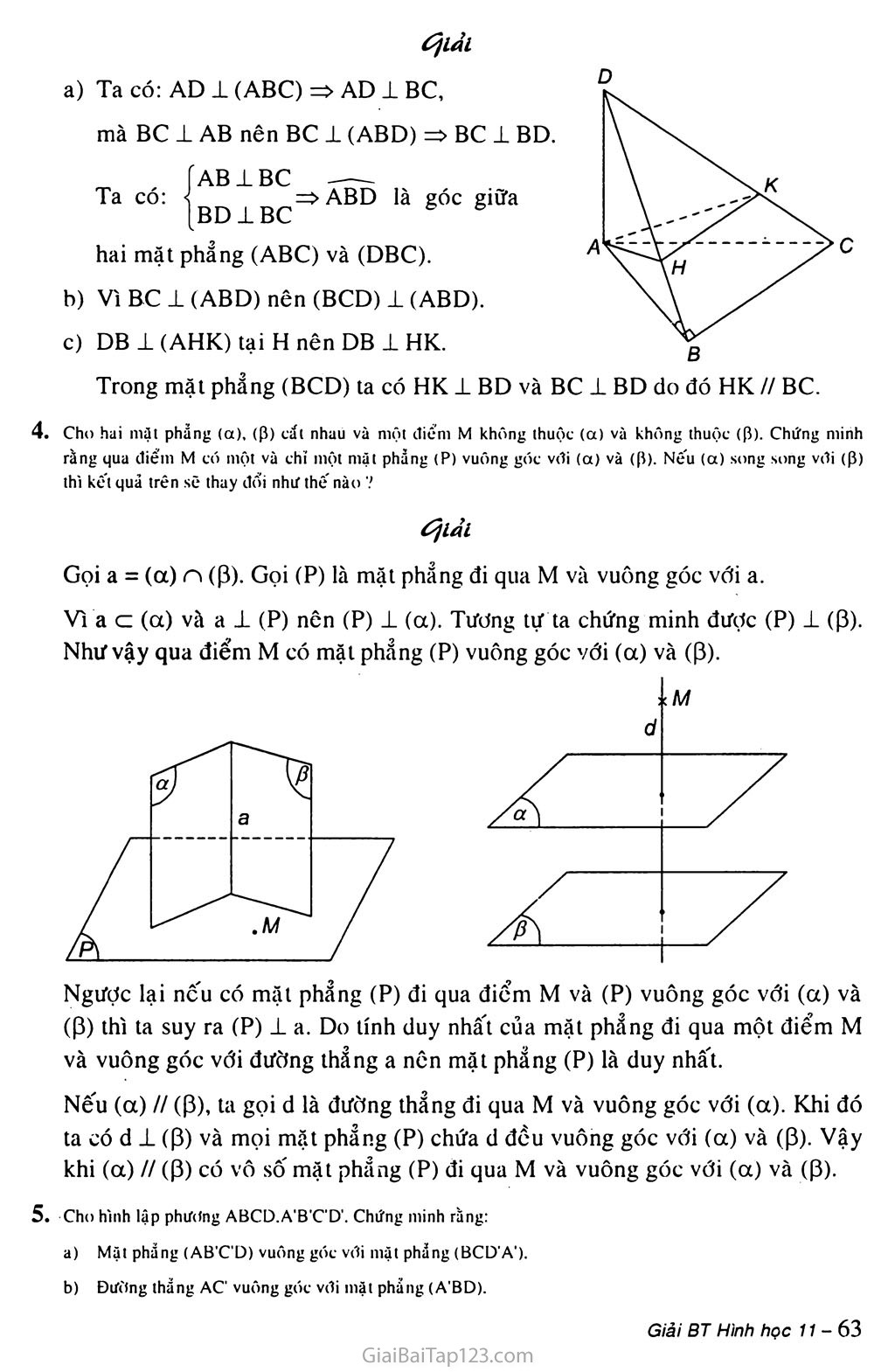
Ta có: AD 1 (ABC) => AD 1 BC, mà BC ± AB nên BC 1 (ABD) => BC 1 BD.
ÍAB1BC
Ta có: => ABD là góc giữa
[BD1BC
hai mặt phẳng (ABC) và (DBC).
Vì BC 1 (ABD) nên (BCD) 1 (ABD).
DB 1 (AHK) tại H nên DB 1 HK.
Trong mặt phẳng (BCD) ta có HK ± BD và BC 1 BD do đó HK // BC.
Cho hai mặt phẫng (a), (P) tắt nhau và một điểnt M không thuộc (a) và không thuộc (p). Chứng minh rằng qua điểm M có một và chí một mặt phẳng (P) vuông góc với (a) và (P). Nếu (a) song song vơi (P) thì kết quả trên sẽ thay đổi như thế nào
ốỊiải
Gọi a = (a) n (P). Gọi (P) là mặt phẳng đi qua M và vuông góc với a.
Vì a c (a) và a 1 (P) nên (P) ± (a). Tương tự ta chứng minh được (P) ± (P). Như vậy qua điểm M có mặt phẳng (P) vuông góc với (a) và (p).
Ngược lại nếu có mặt phẳng (P) đi qua điểm M và (P) vuông góc với (a) và (p) thì ta suy ra (P) ± a. Do tính duy nhất của mặt phẳng đi qua một điểm M và vuông góc với đường thẳng a nên mặt phẳng (P) là duy nhát.
Nếu (a) // (P), ta gọi d là đường thẳng đi qua M và vuông góc với (a). Khi đó ta có d 1 (P) và mọi mặt phẳng (P) chứa d đều vuông góc với (a) và (p). Vậy khi (a) // (P) có vô số mặt phẳng (P) đi qua M và vuông góc với (ct) và (P).
Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:
Mặt phẵng (AB'C'D) vuông góc vơi mặt phẵng (BCD'A').
Đương thẳng AC' vuông góc vơi mặt phảng (A'BD).
ỐỊiải
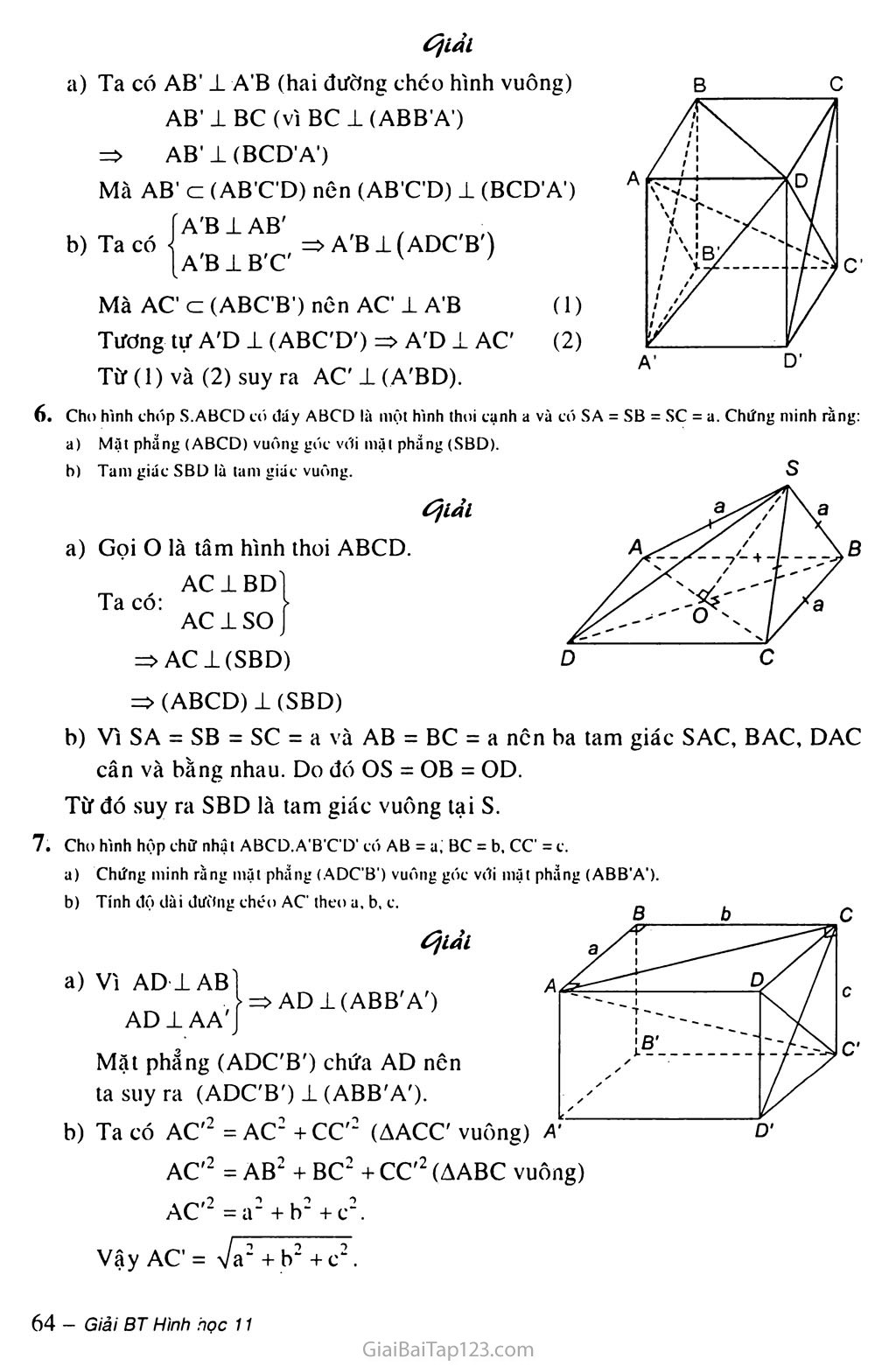
a) Ta có AB' ± A’B (hai đường chéo hình vuông)
AB' 1 BC (vì BC 1 (ABBA/)
=> AB'l(BCD'A')
Mà AB’ c (AB'C'D) nên (AB'C'D) ± (BCDA')
fA'BlAB'
[a'BIB'C'
b) Ta có
A'Bl(ADC'B')
Mà AC'c(ABC'B') nên ACIA'B (1)
Tương tự A'D 1 (ABC'D') => A'D 1 AC' (2)
Từ (1) và (2) suy ra AC' 1 (A'BD).
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = sc = a. Chứng minh ràng:
Mặt phẵng (ABCD) vuông góc vói mạt phẵng (SBD).
Tam giác SBD là tam giác vuông.
Ốịiảl
Gọi o là tâm hình thoi ABCD. s
AC1BDÌ
AC ISO
=> ACl(SBD)
=> (ABCD) 1 (SBD)
Vì SA = SB = SC = a và AB = BC = a nên ba tam giác SAC, BAC, DAC
cân và bằng nhau. Do đó OS - OB = OD.
Từ đó suy ra SBD là tam giác vuông tại s.
Cho hình hộp chữ nhật ABCD.A'B C'D' có AB = a, BC = b, CC' = c.
Chứng minh rằng mặt phẩng (ADCB') vuông góc vời mặt phầng (ABB'A').
Tính độ dài dường chéo AC' theo a, b, c.
a) Vì AD1AB
adiaa;
Mặt phẳng (ADC'B') chứa AD nên
ta suy ra (ADC'B') 1 (ABB'A').
Ta có:
ADl(ABB'A')
b) Ta có AC'2 = AC2 +CC'2 (AACC' vuông) A'
a/ !
>x /
"'id
✓
z
z
✓
✓
z
B
C'
D'
AC'2 = AB2 + BC2 + CC'2 (AABC vuông) AC'2 =a2 + b2 +c2.
Vậy AC’ = Va2 + b2 + c2.
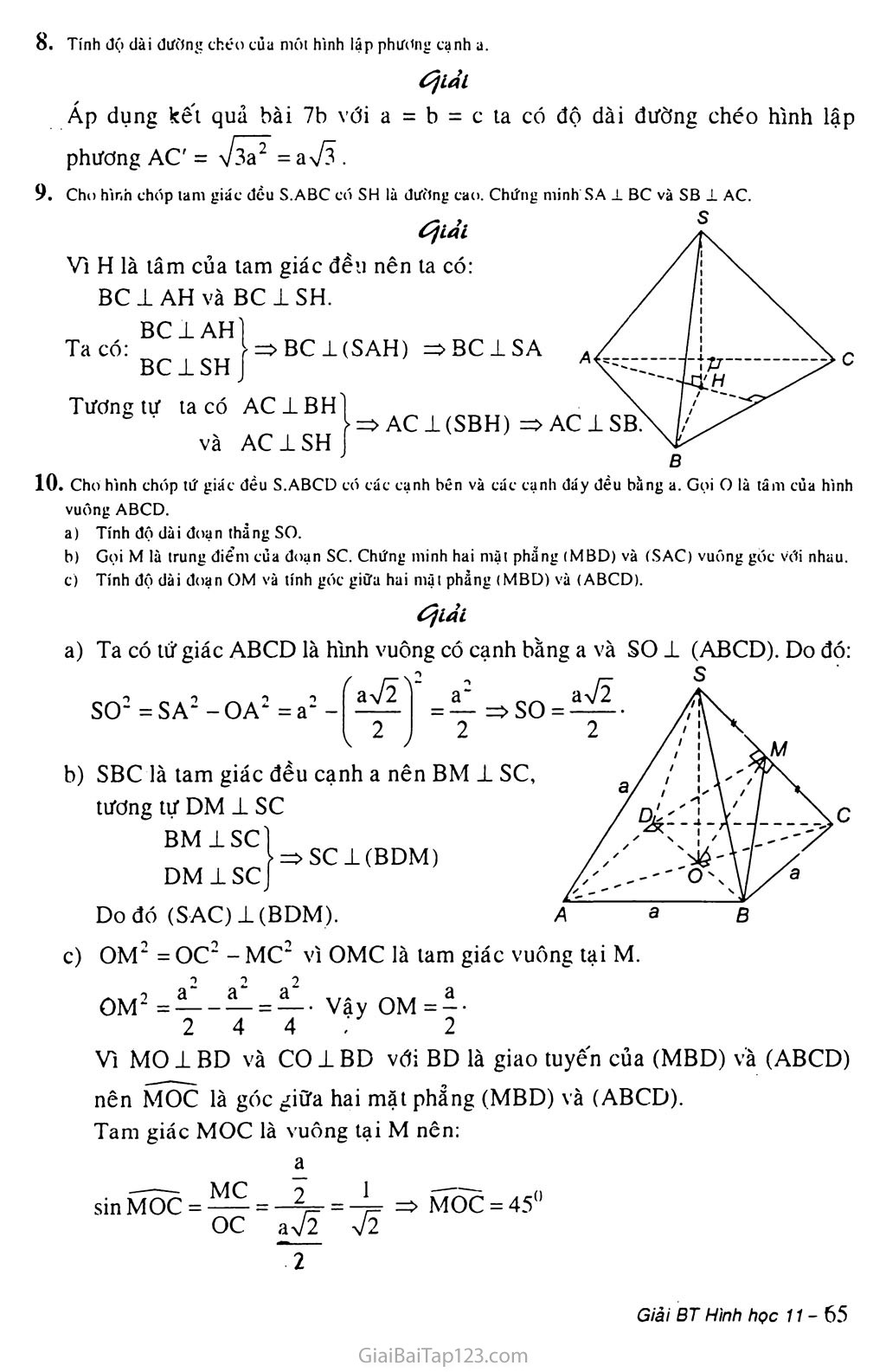
Tính độ dài đường chéo cùa mót hình lập phương cạnh a.
Ốịíải
Áp dụng kết quả bài 7b với a = b = c ta có độ dài đường chéo hình lập phương AC' = v/ởa2 =a7? .
Cho hình chóp lam giác đều S.ABC có SH là dương cao. Chứng minh SA -L BC và SB ± AC.
x;. r. s
■ACl(SBH) => AC1SB.
c/jiai
Vì H là tâm của tam giác đều nên ta có:
BC± AH và BC1SH.
BCl(SAH) =>BC1SA
BC1AHÌ Ta có: * r:
BC1SHJ
Tương tự ta có AC1BH và AC1SH
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi o là tâm cùa hình vuông ABCD.
Tính độ dài đoạn thẳng SO.
Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẩng (MBD) và (SAC) vuông gòc vơi nhau.
Tính độ dài đoạn OM và tính góc giữa hai mặt phẵng (MBD) và (ABCDI.
tflai
Ta có tứ giác ABCD là hình vuông có cạnh bằng a và so ± (ABCD). Do đó:
- ---'O'.
A a B
2 2 2
OM2 =4^- —= —■ Vậy OM = - 2 4 4
OM2 = oc2 - MC2 vì OMC là tam giác vuông tại M.
a
2’
Vì MO 1 BD và CO 1BD với BD là giao tuyến của (MBD) và (ABCD) nên MOC là góc giữa hai mặt phẳng (MBD) và (ABCD).
Tam giác MOC là vuông tại M nên:
a
sin MOC =-^7 = —=-7= => MOC = 45° oc aV2 V2
Vậy góc giữa hai mặt phẳng (MBD) và (ABCD) bằng 45°.
11 . Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và cỏ góc A bằng 60", cạnh sc - ——
và sc vuông góc với mặt phảng (ABCDi.
Chứng minh mặt phẵng (SBDl vuông góc vdi mặt phầng (SAC).
Trong tam giác SCA kẻ IK vuông góc vđi SA tại K. Hãy tính độ dài 1K.
Chứng minh BKD = yO" và từ dó suy ra mặt phẳng (SAB) vuông góc vứi mặt phẵng (SAD).
CA -3A. SA = —-—a
thay vào (1)
Ốịiải
Vì BDTAC và BD1SC nên BDl(SAC). Ta suy ra (SBD)l(SAC).
Hình thoi ABCD được tạo thành bởi hai tam giác đều chung đáy. Hai tam giác vuông SCA và IKA có chung góc A nên đồng dạng, ta có:
IK AI
77 = -—7 (!)
SC AS
Theo định lí Py-ta-go ta có:
o A 2 <-.^-,2 „.2 6a' z rz\- 18a”
SA — sc + CA =—-—b^aV3J —
a Vó a 73
. TV _ SC.AI 2 2 a
SA 372 2
2
SA1DB'
SA1IK
Vì IK = IB = ID = ^
>=>SA±(BDK) =>SA±BK và SA 1 DK.
Vậy BKD là góc giữa hai mặt phẳng (SAB) và (SAD) và BKD = 90° nên ta suy ra (SAB) ±(SAD).
c. BÀI TẬP LẦM THÊM
Cho tam giác ABC vuông càn đỉnh B và AB = a. đoạn SA vuông góc với (ABC) và SA = av/3 . Gọi E và F lần lượt là trung điểm của sc và SB, M là một điểm trôn đoạn AB. Đặt AM = X (0 < X < a). Gọi ct là mặt phẳng chứa EM và vuông góc với (SAB).
Hãy xác định mặt phẳng a và thiết diện của tứ diện SABC với ct.
Chứng minh FM = Vx2 - ax + a 2. Tính diện tích của thiết diện theo a và X.
Cho tam giác đều ABC cạnh a, I là trung điểm của BC, D là điểm đối xứng
của A qua I. Dựng đoạn SD = ~~~ vuông góc với (ABC).
Chứng minh: a) mp(SAB) ± mp(SAC) b) mp(SBC) ± mp(SAD).
Cho hai tam giác ACD và BCD nằm trong hai mặt phẳng vuông góc với nhau, AC = AD = BC = a và CD = 2x. Gọi I và J lần lượt là trung điểm của AB và CD.
Chứng minh rằng IJ vuông góc với AB và IJ vuông góc với CD.
Tính AB và IJ theo a và X.
Xác định X sao cho (ABC) vuông góc với (ABD).