SGK Hình Học 11 - Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song

§2. HAI ĐƯỜNG THẲNG CHÉO NHAƯ VÀ HAI ĐƯỜNG THẲNG SONG SONG
Hình 2.26 cho ta thấy hình ảnh của những đường thẳng song song, đường thẳng chéo nhau. Các khái niệm này sẽ được trình bày sau đây.
À, Quan sát các cạnh tường trong lớp học và xem cạnh tường là hình ảnh của đường thẳng. Hãy chỉ ra một số cặp đường thẳng không thể cùng thuộc một mặt phẳng.
Hình 2.26
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THANG trong không gian
Cho hai đường thẳng a và. b trong không gian. Khi đó có thể xảy ra một trong hai trường hợp sau.
Khi đó ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng có ba khả năng sau đây xảy ra (h.2.27).
a n b = {M}	allb	a = b
Hình 2.27
Trưởng hợp 1. Có một mặt phẳng chứa a và b.
a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và
kí hiệu là a n b = {m} . Ta còn có thể viếtanb = M.
a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.
a trùng b, kí hiệu là a = b.
Như vậy, hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chưng.
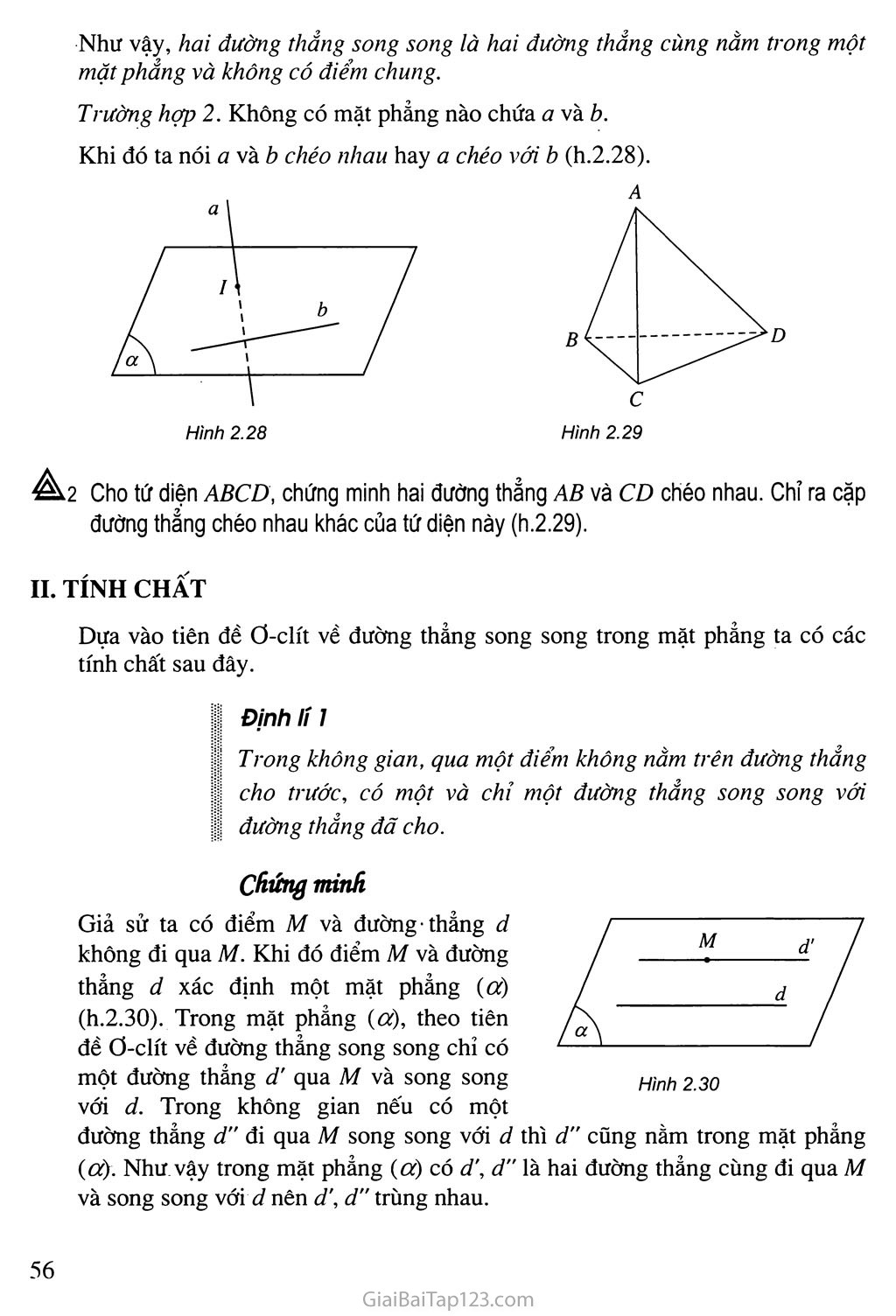
Trường hợp 2. Không có mặt phẳng nào chứa a và b.
Khi đó ta nói avằb chéo nhan hay a chéo với b (h.2.28).
a2 Cho tứ diện ABCD, chứng minh hai đường thẳng AB và CD chéo nhau. Chỉ ra cặp đường thẳng chéo nhau khác của tứ diện này (h.2.29).
TÍNH CHẤT
Dựa vào tiên đề ơ-clít về đường thẳng song song trong mặt phẳng ta có các tính chất sau đây.
I Định lí 1
Trong không gian, qua một điểm không nằm trên đường thẳng ' cho trước, có một và chỉ một đường thẳng song song với I đường thẳng đã cho.
chứng minh
Hình 2.30
thì d" cũng nằm trong mặt phẳng là hai đường thẳng cùng đi qua M
Giả sử ta có điểm M và đường-thẳng d không đi qua M. Khi đó điểm M và đường thẳng d xác định một mặt phẳng (cộ (h.2.30). Trong mặt phẳng (cộ, theo tiên đề ơ-clít về đường thẳng song song chỉ có một đường thẳng d' qua M và song song với d. Trong không gian nếu có một đường thẳng d" đi qua M song song với d (cộ. Như vậy trong mặt phảng (cr) có d', d" và song song với d nên d', d" trùng nhau.
Hình 2.31
Nhận xét. Hai đường thẳng song song a và b xác định một mặt phẳng, kí hiệu là mp (ứ, b) hay (a, b) (h.2.31).
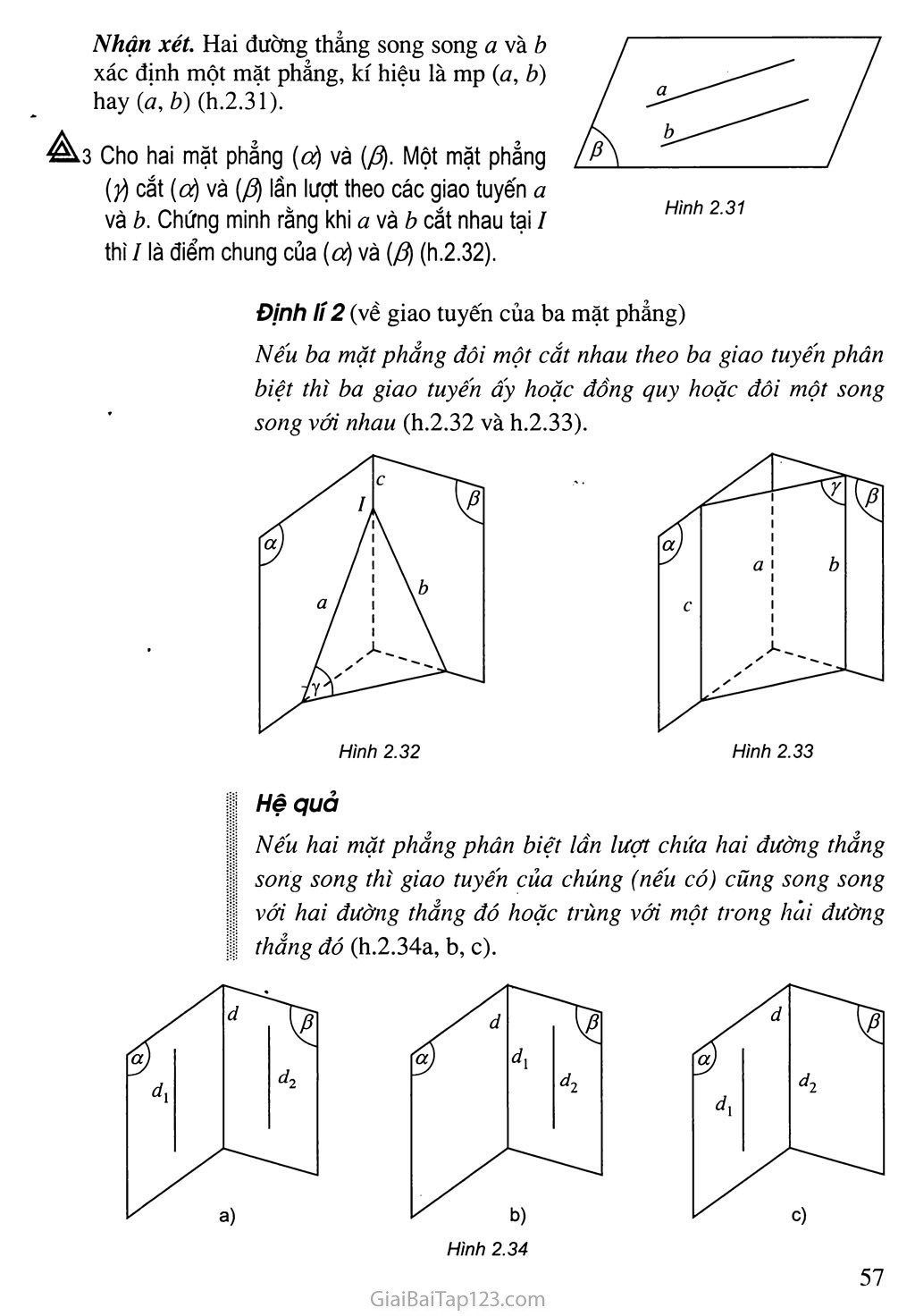
As Cho hai mặt phẳng (ữộ và ($. Một mặt phẳng (jộ cắt (a) và (P) lần lượt theo các giao tuyến a và b. Chứng minh rằng khi a và b cắt nhau tại / thì ỉ là điểm chung của (a) và ($ (h.2.32).
I Định lí 2 (về giao tuyến của ba mặt phẳng)
I Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân I ồz'ệr thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song
song với nhau (h.2.32 và h.2.33).
Hệ quả
ị Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng II song song thì giao tuyến của chúng (nếu có) cũng song song II với hai đường thẳng đó hoặc trùng với một trong hài đường ị thẳng dó (h.2.34a, b, c).
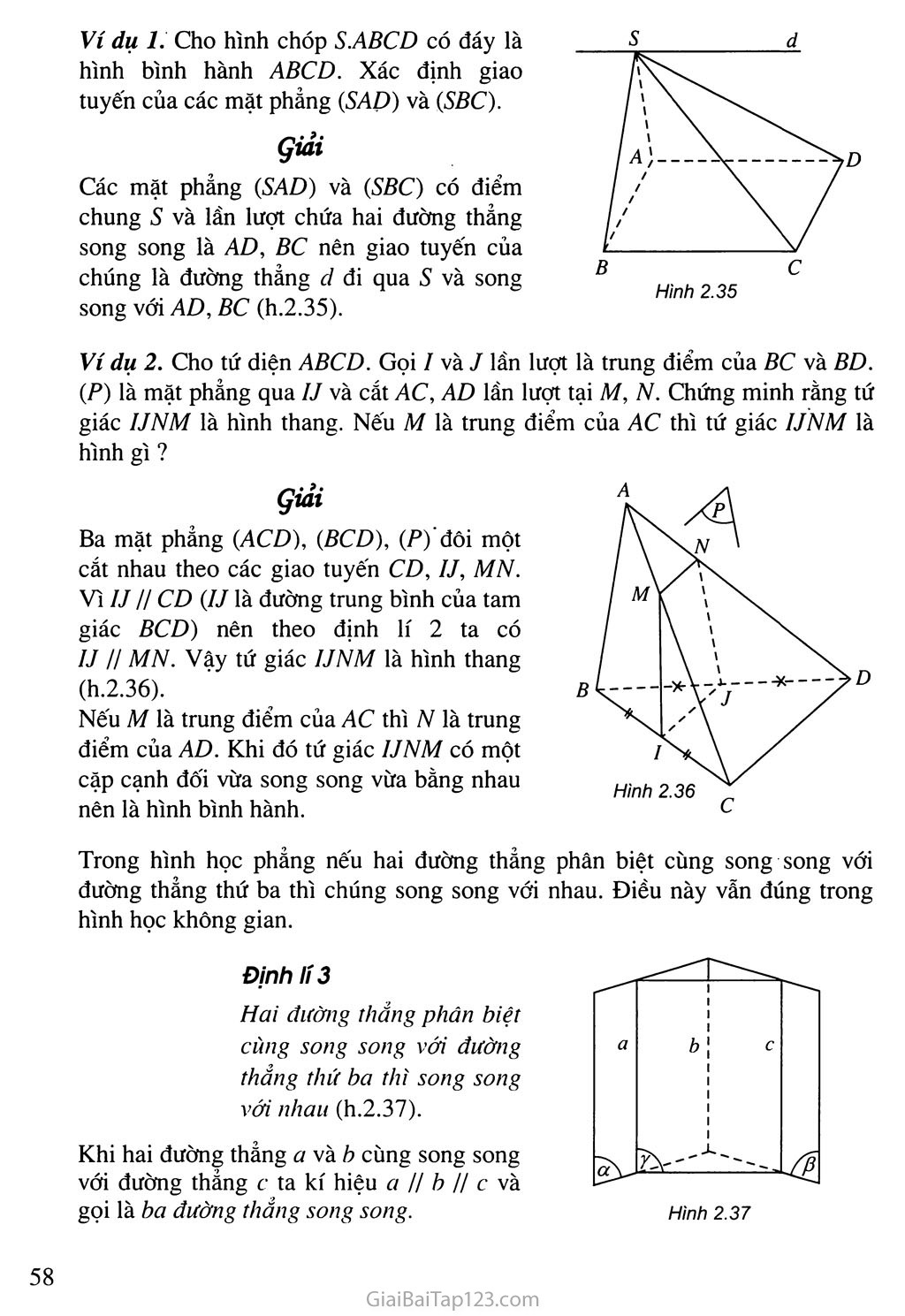
Ví dụ 1. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Xác định giao tuyến của các mặt phẳng (SAD) và (SBC).
giải
Các mặt phẳng (SAD) và (SBC) có điểm chung 5 và lần lượt chứa hai đường thẳng song song là AD, BC nên giao tuyến của chúng là đường thẳng d đi qua s và song song với AD, BC (h.2.35).
d
s
Hình 2.35
Ví dụ 2. Cho tứ diện ABCD. Gọi / và 7 lần lượt là trung điểm của BC và BD. (P) là mặt phẳng qua IJ và cắt AC, AD lần lượt tại M, N. Chứng minh rằng tứ giác UNM là hình thang. Nếu M là trung điểm của AC thì tứ giác IJNM là hình gì ?
Ba mặt phẳng (ACD), (BCD), (P) đôi một cắt nhau theo các giao tuyến CD, IJ, MN. Vì IJ // CD (IJ là đường trung bình của tam giác BCD) nên theo định lí 2 ta có IJ // MN. Vậy tứ giác UNM là hình thang (h.2.36).
Nếu M là trung điểm của AC thì V là trung điểm của AD. Khi đó tứ giác UNM có một cặp cạnh đối vừa song song vừa bằng nhau nên là hình bình hành.
Trong hình học phẳng nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. Điều này vẫn đúng trong hình học không gian.
I Định lí 3
Hai đường thẳng phân biệt I củng song song với đường I thẳng thứ ba thì song song
với nhau (h.2.37).
Khi hai đường thẳng a và b cùng song song với đường thẳng c ta kí hiệu ữ // b II c và gọi là ba đường thẳng song song.
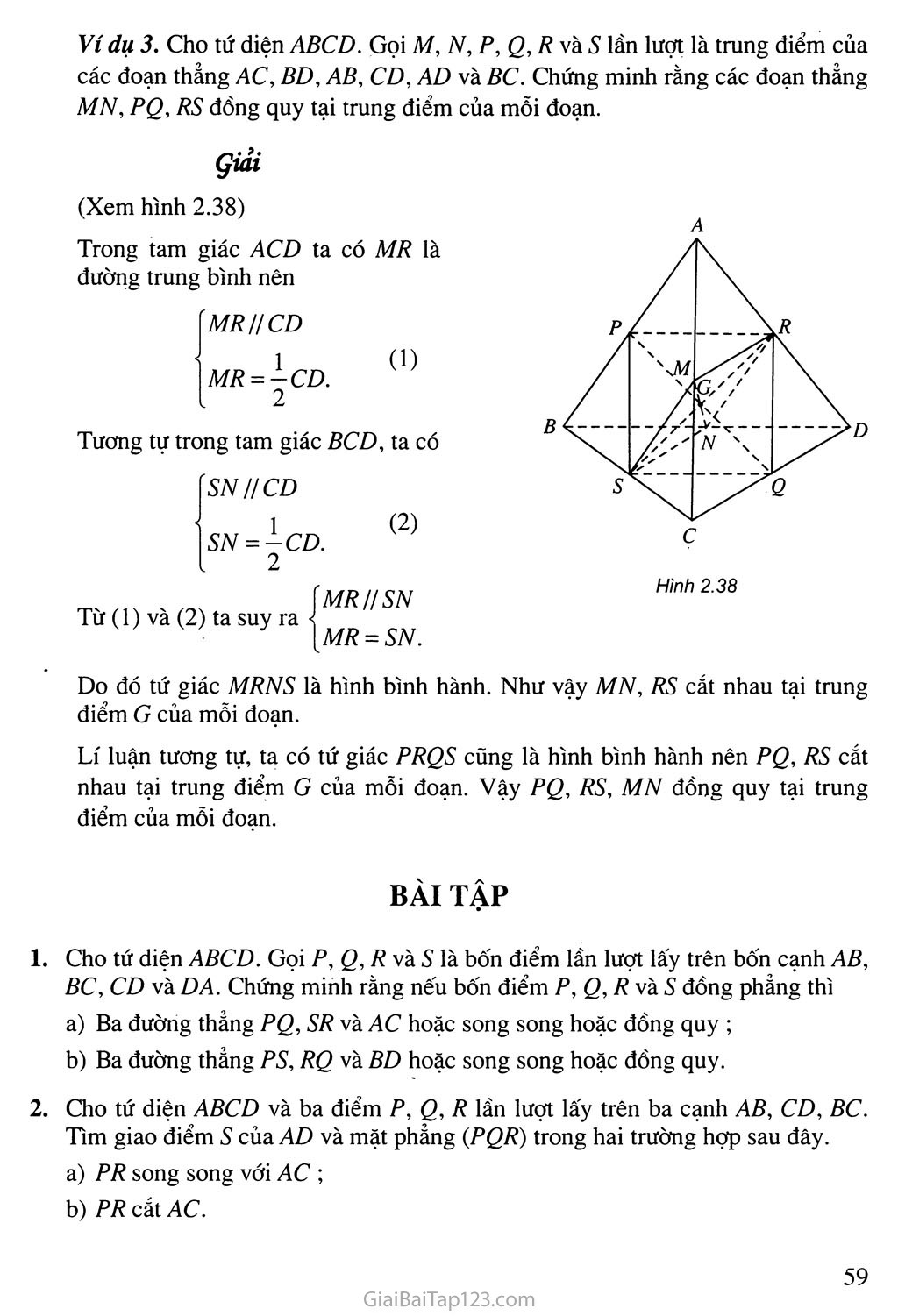
Ví dụ 3. Cho tứ diện ABCD. Gọi M, N, p, Q,RvàS lần lượt là trung điểm của các đoạn thẳng AC, BD, AB, CD, AD và BC. Chứng minh rằng các đoạn thẳng MN, PQ, RS đồng quy tại trung điểm của mỗi đoạn.
Hình 2.38
(Xem hình 2.38)
Trong tam giác ACD ta có MR là đường trung bình nên
MRHCD
1 (1) MÃ = 4 CD.
2
SN = ịcD.
2
(2)
Từ (1) và (2) ta suy ra
MR//SN MR = SN.
Tương tự trong tam giác BCD, ta có
SN//CD
Do đó tứ giác MRNS là hình bình hành. Như vậy MN, RS cắt nhau tại trung điểm G của mỗi đoạn.
Lí luận tương tự, ta có tứ giác PRQS cũng là hình bình hành nên PQ, RS cắt nhau tại trung điểm G của mỗi đoạn. Vậy PQ, RS, MN đồng quy tại trung điểm của mỗi đoạn.
BÀI TẬP
Cho tứ diện ABCD. Gọi p, Q, RvàS là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD và DA. Chứng minh rằng nếu bốn điểm p, Q, R và s đồng phẳng thì
Ba đường thẳng PQ, SR và AC hoặc song song hoặc đồng quy ;
Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy.
Cho tứ diện ABCD và ba điểm p, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Tìm giao điểm s của AD và mặt phẳng (PQR) trong hai trường họp sau đày.
PR song song với AC ;
PR cắt AC.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
Tìm giao điểm A' của đường thẳng AG và mặt phẳng (BCD).
Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M'. Chứng minh B, M', A' thẳng hàng và BM' = M'A' = A'N.
Chứng minh GA = 3GA'.