SGK Hình Học 11 - Bài 4. Hai mặt phẳng song song

§4. HAI MẶT PHẲNỌ song song
I. ĐỊNH NGHĨA
Hai mặt phẳng (ạ), (/5) được gọi là song song với nhau nếu chúng không có điểm chung.
Khi đó ta kí hiệu (a) // (/?) hay (ft) II (cộ	Hình 246
Nếu mặt phẳng (ứ) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (j3) thì (cộ song song với 1/3).
chứng minh
Gọi M là giao điểm của a và b.
Vì (ợ) chứa a mà a song song với 1/3) nên (cộ và 1/3} là hai mặt phẳng phân biệt. Ta cần chứng minh (cộ song song với (/?).
b
Hình 2.48
Giả sử (ộ) và (yổ) không song song và cắt nhau theo giao tuyến c (h.2.48). Ta có
«//(£)
c // a
cllb.
(a) D a (a)rMJ3) = c
và •
b//(P)
(ữf) D b (a)n(fi) = c
Như vậy từ M ta kẻ được hai đường thẳng a, b cùng song song với c. Theo định lí 1, §2, điều này mâu thuẫn. Vậy (ơ) và (fi) phải song song với nhau.
Á2 Cho tứ diện SABC. Hãy dựng mặt phẳng (ới) qua trung điểm I của đoạn SA và song song với mặt phẳng (ABC).
giải
Ví dụ 1. Cho tứ diện ABCD. Gọi GpG2,G3 lần lượt là trọng tâm của các tam giác ABC, ACD, ABD. Chứng minh mặt phẳng (GjG2G3) song song với mặt phẳng (BCD).
AG, AGọ
Do đó —7 = -—7 suy ra GỵG^IIMN.	Hình 2.49
AM AN
Vì MN nằm trong (BCD) nên GjG2 II(BCD).
AG, AGq	„
Tương tự —77 = ——7 suy ra G.GtII MP. vì MP nằm trong (BCD) nên
AM AP	3
G1G3//(BCD.). Vậy (G1G2G3)//(BCD).
Ta biết rằng qua một điểm không thuộc đường thẳng d có duy nhất một đường thẳng d' song song với d. Nếu thay đường thẳng d bởi mặt phẳng (cộ thì được kết quả sau.
I Định lí 2
I Qua một điểm nằm ngoài một I mặt phẳng cho trước có một và chỉ một mặt phẳng song song
I với mặt phẳng đã cho (h.2.50). Từ định lí trên ta suy ra các hệ quả sau.
Hệ quả 1
Nêu đường thẳng d song song với mặt phẳng (ự) thì qua d có duy nhất một mặt phẳng song song với (cộ (h.2.51).
Hình 2.50
Hình 2.51
Hệ quả 2
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
Hệ quả 3
Cho điểm A không nằm trên mặt phẳng (cộ. Mọi đường thẳng đi qua A và song song với (cố) đều nằm trong mặt phẳng đi qua A và song song với (cộ (h.2.52).
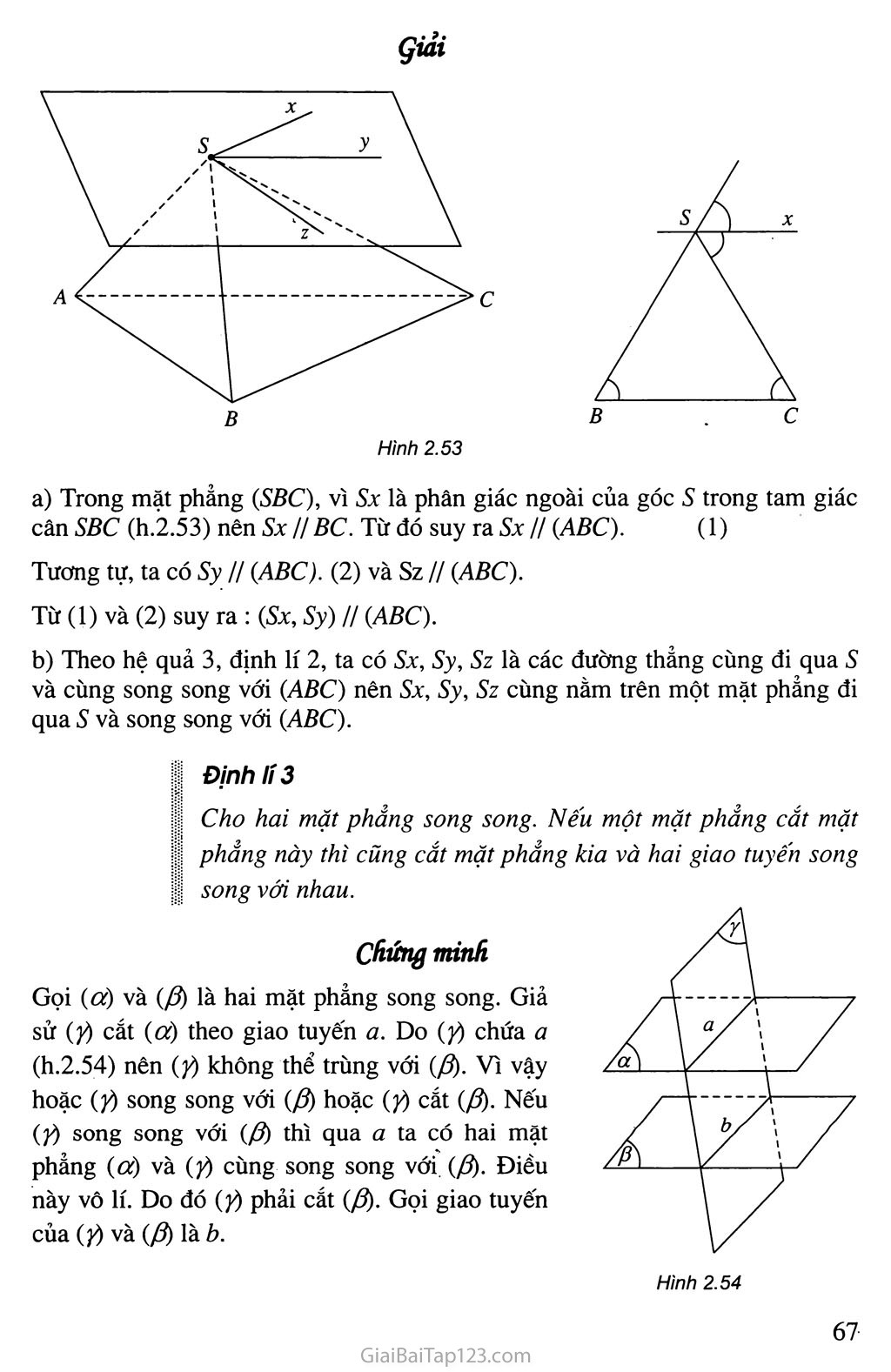
Ví dụ 2. Cho tứ diện SABC có SA = SB = sc. Gọi Sx, Sy, Sz lần lượt là phân giác ngoài của các góc s trong ba tam giác SBC, SCA, SAB. Chứng minh :
Mặt phẳng (Sx, Sỳ) song song với mặt phẳng (ABC);
Sx, Sy, Sz cùng nằm trên một mặt phẳng.
Trong mặt phẳng (SBC), vì Sx là phân giác ngoài của góc s trong tam giác cân SBC (h.2.53) nên Sx IIBC. Từ đó suy ra Sx II (ABC). (1)
Tương tự, ta có Sy H (ABC). (2) và Sz // (ABC).
Từ (1) và (2) suy ra : (Sx, Sy) II (ABC).
Theo hệ quả 3, định lí 2, ta có S.Y, Sy, Sz là các đường thẳng cùng đi qua s và cùng song song với (ABC) nên Sx, Sy, Sz cùng nằm trên một mặt phẳng đi qua s và song song với (ABC).
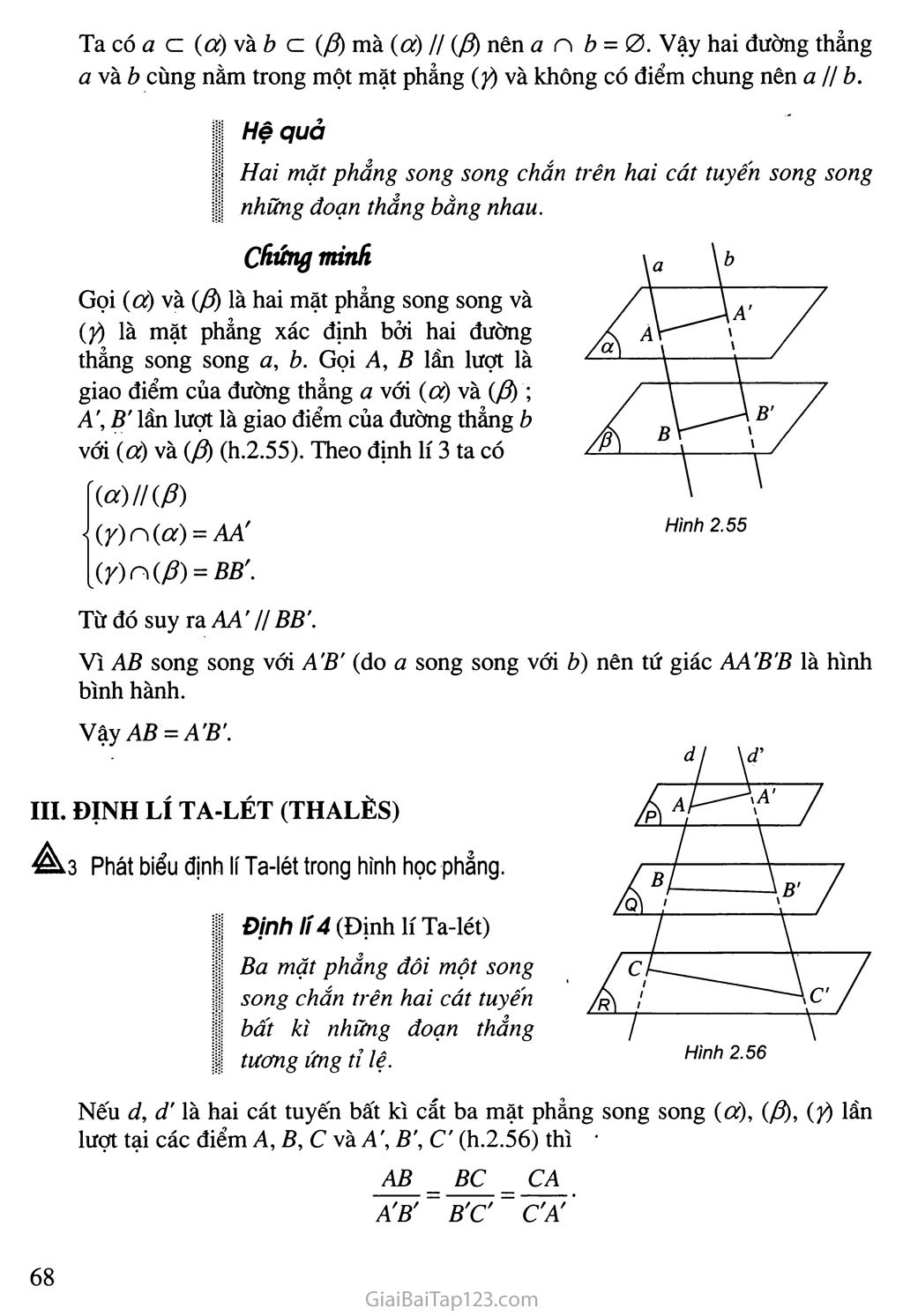
Định lí 3
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt I phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song I song với nhau.
Chứng minh
Gọi (à) và (ft) là hai mặt phẳng song song. Giả sử (ý) cắt (à) theo giao tuyến a. Do (ý) chứa a (h.2.54) nên (ỳ) không thể trùng với (ft). Vì vậy hoặc (ý) song song với (ft) hoặc (ý) cắt (ft). Nếu (ỳ) song song với (ft) thì qua a ta có hai mặt phẳng (à) và (ý) cùng song song với, (ft). Điều này vô lí. Do đó (y) phải cắt (ft). Gọi giao tuyến của (ỹ) và (ft) là b.
Ta có a c (cộ và b c (/3) mà (cộ // (yổ) nên a n b = 0. Vậy hai đường thẳng a vầb cùng nằm trong một mặt phẳng (ỳ) và không có điểm chung nên a // b.
I Hệ quả
Hai mặt phẳng song song chắn trên hai cát tuyêh song song những đoạn thẳng bằng nhau
CHứngminã
Gọi (cộ và (fi) là hai mặt phẳng song song và (ỳ) là mặt phẳng xác định bởi hai đường thẳng song song a, b. Gọi A, B lần lượt là giao điểm của đường thẳng a với (cộ và (yổ);
A', B' lần lượt là giao điểm của đường thẳng b với (cộ và (/ộ (h.2.55). Theo định lí 3 ta có
'(«)//(/?)
• (/)n(cr) = AA' ír)^j3) = BB'.
Từ đó suy ra AA 7/ BB
Vì AB song song với A’B' (do a song song với b) nên tứ giác AA'B'B là hình bình hành.
VậyAB = A'B'.
ĐỊNH LÍ TA-LÉT (THALÈS)
^3 Phát biểu định lí Ta-lét trong hình học phẳng.
I Định /z'4 (Định lí Ta-lét)
I Ba mặt phẳng đôi một song I song chắn trên hai cát tuyến ' bất kì những đoạn thẳng I tương ứng tỉ lệ.
Nếu d, d' là hai cát tuyến bất kì cắt ba mặt phẳng song song (cc), (yổ), (ỳ) lần lượt tại các điểm A, B, c và A', B', C' (h.2.56) thì •
AB _ fiC _ CA
Ã# " B'c' - C'A' ’
HÌNH LĂNG TRỤ VÀ HÌNH HỘP
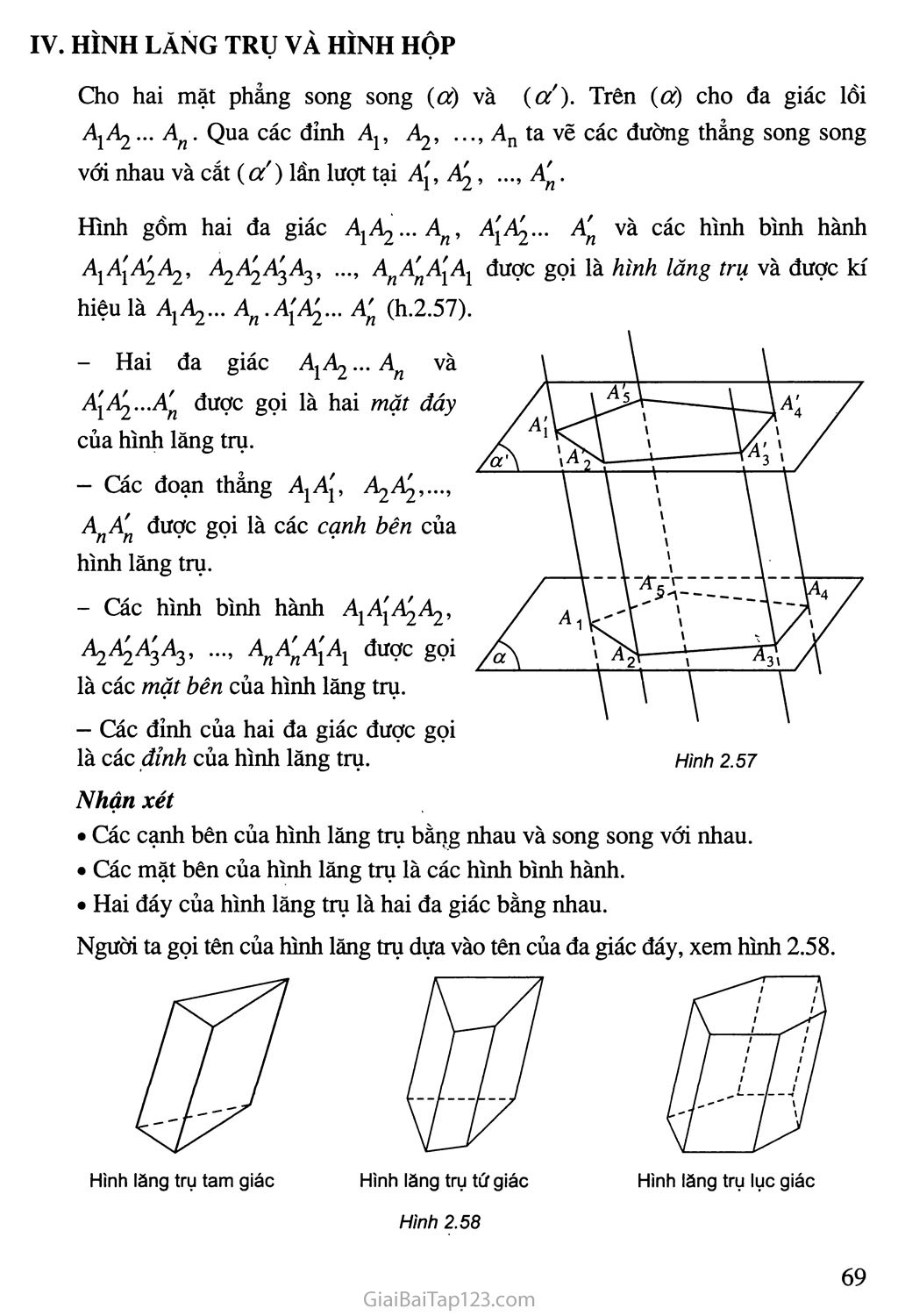
Cho hai mặt phẳng song song (Of) và (Of'). Trên (Of) cho đa giác lồi AịA2... An. Qua các đỉnh Ap Aj, ..., An ta vẽ các đường thẳng song song với nhau và cắt (Of') lần lượt tại Ap , ..., A'.
Hình gồm hai đa giác AỵA^... An, AỵA^... A'n và các hình bình hành AjAj'A^Aj, A^A^A^At,, ..., A^A'AjAj được gọi là hình lăng trụ và được kí hiệu là AỵA^... An.AýA^... A'n (h.2.57).
Hai đa giác AỵA^... An và AjA^...A' được gọi là hai mặt đáy của hình lăng trụ.
Các đoạn thẳng AjAp A^A^,...,
AnA'n được gọi là các cạnh bên của hình lăng trụ.
Các hình bình hành AjAjA^A^,
AyA^A^Ay ..., A A'AjAj được gọi là các mặt bên của hình lăng trụ.
Các đỉnh của hai đa giác được gọi
là các đỉnh của hình lăng trụ.	Hình 2.57
Nhận xét
Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
Các mặt bên của hình lăng trụ là các hình bình hành.
Hai đáy của hình lăng trụ là hai đa giác bằng nhau.
Người ta gọi tên của hình lăng trụ dựa vào tên của đa giác đáy, xem hình 2.58.
• Hình lăng trụ có đáy là hình tam giác được gọi là hình lăng trụ tam giác.
• Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp (h.2.59).
HÌNH CHÓP CỤT
Định nghĩa
Cho hình chóp S.AịA^.-.A^ ; một mặt
phẳng (P) không qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh SAp SA}, SAn lần lượt tại Ap A^, A'. Hình tạo bởi thiết diện A[A^ ... A' và đáy Aj A? ... An của hình chóp cùng với các tứ giác AịA^AợA,, A^A^A^A^, ..., A'AjAjA^ gọi là hình chóp cụt (h.2.60).
Hình 2.60
Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện AjA^... A' gọi là đáy nhỏ của hình chóp cụt. Các tứ giác A'1A^A2A1, A^A^AgAj, ..., A'AjAjA/? gọi là các mặt bên của hình chóp cụt. Các đoạn thẳng AjAp AjA^,..., AnA'n gọi là các cạnh bên của hình chóp cụt.
Tuỳ theo đáy là tam giác, tứ giác, ngũ giác ..., ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chóp cụt ngũ giác,...
Vì hình chóp cụt được cắt ra từ một hình chóp nên ta dễ dàng suy ra các tính chất sau đây của hình chóp cụt.
I Tính chất
I l) Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ sô'các cặp cạnh tương ứng bằng nhau.
I 2) Các mặt bên là những hình thang.
I 3) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.
BÀI TẬP
Trong mặt phẳng (ũộ cho hình bình hành ABCD. Qua A, B, c, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên (ậ). Trên a, b, c lần lượt lấy ba điểm A', B', C' tuỳ ý.
Hãy xác định giao điểm D' cùa đường thẳng d với mặt phẳng {A'B'C^.
Chứng minh A'B'C'D’ là hình bình hành.
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M và M' lần lượt là trung điểm của các cạnh BC và B'C'.
Chứng minh rằng AM song song với A'M'.
Tìm giao điểm của mặt phẳng (AS'C') với đường thẳng A'M.
Tìm giao tuyến d của hai mặt phẳng (AB'Cr) và (BA'C').
Tìm giao điểm G của đường thẳng d với mặt phẳng (ẠM'MỴ Chứng minh G là trọng tâm của tam giác AB'C.
Cho hình hộp ABCD.A B'C'D
Chứng minh rằng hai mặt phẳng (BDAr) và (B'D'C) song song với nhau.
Chứng minh rằng đường chéo AC' đi qua trọng tâm Gj và Gọ của hai tam giác BDA' và B'D'C.
Chứng minh Gj và G2 chia đoạn AC' thành ba phần bằng nhau.
Gọi o và I lần lượt là tâm của các hình bình hành ABCD và AA'C'C. Xác định thiết diện của mặt phẳng (Â7Ơ) với hình hộp đã cho.
Cho hình chóp S.ABCD. Gọi Â] là trung điểm của cạnh SA và Â2 là trung điểm của đoạn ÂÂ|. Gọi (cộ và (/3) là hai mặt phẳng song song với mặt phẳng (ÂBCD) và lần lượt đi qua Aị,A2. Mặt phẳng (à) cắt các cạnh SB, sc, SD lần lượt tại Bị, Cị, Dị. Mặt phẳng {/3} cắt các cạnh SB, sc, SD lần lượt tại B2, c2, D2. Chứng minh :
Bỵ, Cỵ, Dỵ lần lượt là trung điểm của các cạnh SB, sc, SD ;
BXB2 = B2B, C]C2 — C2C, DỵD2 — D2D j
Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.